AsI3电子结构与弹性性质的第一性原理研究

孙霄霄， 李敏君， 赵祥敏， 陈玉强， 李 聪

(1. 牡丹江师范学院工学院， 牡丹江 157012； 2.牡丹江师范学院理学院， 牡丹江 157012)

AsI3电子结构与弹性性质的第一性原理研究

孙霄霄1， 李敏君1， 赵祥敏1， 陈玉强1， 李 聪2

(1. 牡丹江师范学院工学院， 牡丹江 157012； 2.牡丹江师范学院理学院， 牡丹江 157012)

采用基于密度泛函理论的第一性原理赝势方法，对AsI3的平衡态晶格常数、弹性常数和电子结构进行了研究. 研究结果表明，R-3结构的AsI3在零压下是稳定的，优化得到的平衡结构参数与实验值符合的很好. AsI3是脆性材料，具有大的弹性各向异性特征. R-3相AsI3的块体模量、剪切模量和杨氏模量分别为14.2 GPa, 9.8 GPa和23.9 GPa，泊松比为0.22，德拜温度是163 K. 能带结构计算表明，AsI3是带隙为2.34 eV的间接带隙半导体. AsI3的化学键是弱共价键和离子键的混合.

AsI3； 各向异性； 第一性原理； 电子性质

1 引 言

AsI3是空间群为R-3的菱方结构. 菱方结构的AsI3可以被看作是三层堆积结构，三层中的每一层是由三原子平面(I-As-I平面)构成. I原子近似地成六角密堆积排列，As原子大大偏离I原子成键构成的八面体的中心，As周边只有3个最近邻的I原子. 因此，AsI3晶体结构也可以被看作是由AsI3分子构成.

随着光电子、声光电子和微电子技术的发展，具有层状结构的材料被广泛关注. 目前，具有层状结构的金属卤化物，包括BiI3，SbI3和AsI3引起了人们浓厚的研究兴趣[1-3]. 对于AsI3晶体，目前的研究主要集中在其晶体结构上[4,5]. 2002年，Virko等人分别使用密度函数方法(MPW1PW和B3LYP)和第一性原理从头算方法(HF和MP2)研究了金属碘化物MI3(M=As, Sb, Bi)的分子结构和振动谱[6]. 2010年，Trotter计算得到的晶格常数a为7.208 Å,c为21.436 Å[7]. 1996年，Anderson等人利用拉曼散射实验测得室温下AsI3在1.6 GPa发生结构相变[8]. 2000年，利用金刚石压砧技术，Saitoh等人通过拉曼散射实验测定AsI3在温度为77K时的结构相变压强为1.66 GPa[9]. 尽管对AsI3的晶体结构进行了大量研究，但仍有一些基本问题没有解决，许多基本性质仍是未知的. 例如，菱方结构晶体的弹性常数测量很困难，至今还未有关于AsI3弹性常数的实验数据和相关的理论报道；涉及电子性质方面的理论研究也非常少；与实验数据相比，一个完整的能够描述AsI3高压结构相变的理论方法仍然缺乏. 因此，本文采用基于密度泛函理论的第一性原理赝势方法，对AsI3的晶体结构、弹性模量和相关电子性质进行了第一性原理计算研究. 通过弹性常数计算了相关的力学性质模量，分析相关力学性质，补充了关于力学性质研究的空白，为这类材料的应用提供了一些依据.

2 计算方法

本文计算是从第一性原理出发，采用基于密度泛函理论的平面波赝势方法进行的，使用CASTEP软件包完成所有的计算[10,11]. 电子的交换关联势选取广义梯度近似(GGA)下的PBE函数形式，电子和离子之间的相互作用采用超软赝势(USPP)方法，平面波截断能取320 eV以保证足够收敛[12,13]. 在结构优化中，能量收敛精度为5.0×10-6eV/atom，容许原子的最大位移是5.0×10-4Å，内应力不大于0.02 GPa，每个原子的最大受力为0.01 eV/Å，自洽(SCF)计算的收敛阈值为5.0×10-7eV/atom. 采用BFGS算法对晶体结构进行优化.

弹性常数的计算采用线性响应理论框架下的有限应变理论来完成. 通过弹性常数，根据Voigt-Reuss-Hill理论(VRH)[14]可以计算出体模量B(GPa)、剪切模量G(GPa)、弹性模量E(GPa)、泊松比ν和德拜温度θD(K). 在弹性模量计算中，存在Voigt理论和Reuss理论.BV和GV分别表示Voigt理论下的体模量和剪切模量，BR和GR分别表示Reuss理论下的体模量和剪切模量.

Voigt 理论下，BV、GV分别为：

9BV=(C11+C22+C33)+2(C12+C23+C31),

(1)

15GV=(C11+C22+C33)-(C12+C23+C31)+

3(C44+C55+C66),

(2)

Reuss理论下，BR和GR分别为：

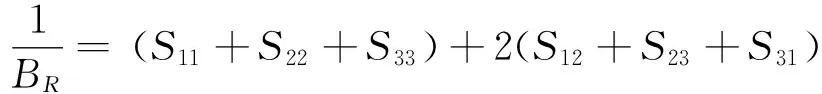
(3)

3(S44+S55+S66),

(4)

对于菱方结构晶体，

(5)

15GV=(2C11+C33)-(C12+2C13)+

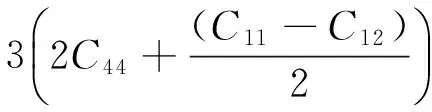
(6)

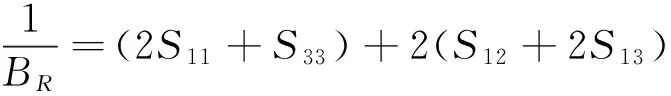
(7)

3(2S44+S66)，

(8)

采用Hill平均计算体模量B和剪切模量G，如下式：

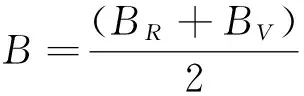
(9)

对于各向同性材料，E和ν可由下式估算：

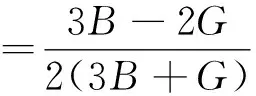
(10)

3 结果与分析

3.1 结构特性分析

本文选用的计算模型是具有菱方结构的AsI3，对应的空间群为R-3. 在这个结构中，每个晶胞中都包含2个As原子和6个I原子. 晶胞结构如图1所示. 经过几何优化，计算得到的零压下R-3结构的晶格参数，以及可用的实验值列于表1. 从表1中，我们可以清晰的看出：本文得到的晶格常数a=b=7.421 Å和c=22.127 Å，与实验值a=b=7.248 Å和c=21.548 Å符合的很好，误差分别为2.4%和2.7%. 这表明我们采用的计算方法是可靠的. 从计算所得的数据中也可以看出，采用GGA近似进行计算会高估晶格常数. 在R-3结构中，As原子占据Wyckoff网格点的6c(0.1913, 0.1913, 0.1913)位置，I原子位于18f(0.4362, 0.0551, -0.2325)位置.

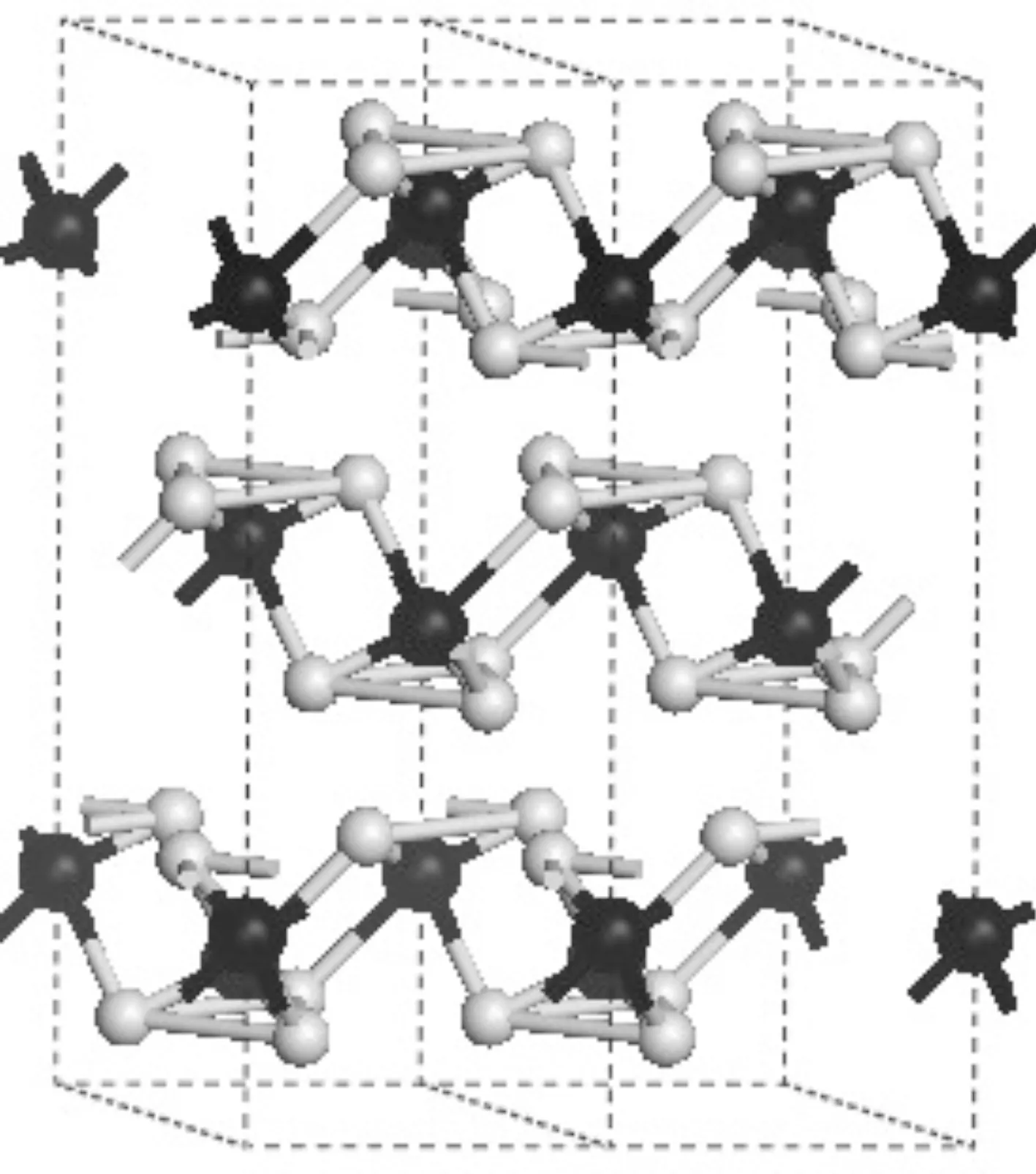
图1 R-3相AsI3的晶体结构 (深色球表示As原子，浅色球表示I原子)Fig. 1 Conventional unit cells of AsI3 with rhombohedral R-3 phase. (The dark and light balls represent arsenic and iodide atoms, respectively.)

表1 AsI3的平衡结构参数.a和c是晶格常数，V0是单胞体积，ρ是密度，H是单个分子的焓

Table 1 The equilibrium crystal structural parameters for AsI3.aandcare lattice parameters,V0is unit cell volume,ρis the density,His the single molecular enthalpy

SpacegroupH/eVV0/Å3a/Åc/Åρ/g.cm-3Ref.R-3-1125.396175.9163.47.4217.24822.12721.5474.304.63ThisworkExpt.[15]

3.2 弹性特征分析

众所周知，固体的弹性性质非常重要，它与各种固态现象密切相关，比如固体内部原子势、状态方程和声子谱等[16]. 弹性性质在热力学上也同比热、热膨胀、德拜温度、Grüneisen参数等相关.

我们计算了零压下R-3相AsI3的弹性常数，通过弹性常数，根据Voigt-Reuss-Hill理论 (VRH) 计算出块体模量、剪切模量、杨氏模量和泊松比，结果如表2所示. 遗憾的是，目前尚没有AsI3体模量、剪切模量和杨氏模量的实验数据或理论数据同本文的结果进行对比.

表2 零压下，R-3相AsI3的弹性常数Cij/ GPa、块体模量B/GPa、剪切模量G/ GPa、杨氏模量E/ GPa、泊松比ν和德拜温度θD/ K

Table 2 The calculated zero-pressure elastic constantsCij/ GPa, the isotropic bulk modulusB/GPa, shear modulusG/ GPa, Young’ modulusE/ GPa, Poisson's ratioν, and Debye temperatureθD/ K for the R-3 phase of AsI3

SpacegroupC11C33C44C12C13C14BGEνθD(K)R-337.414.110.013.17.4-2.914.29.823.90.22163

菱方结构的晶体，有6个独立弹性常数(C11，C12，C13，C14，C33和C44)，需要满足的Born-Huang力学稳定标准为[17]：

C33>0,C44>0,C11-|C12|>0,

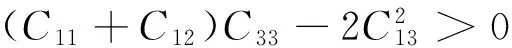
(11)

经计算发现，R-3相AsI3在零压下满足力学稳定标准，是力学稳定的.

AsI3的体模量为14.2GPa. 通过后面的分析我们发现在R-3结构中，As和I之间形成较弱的离子键，因此体模量较小. 杨氏模量可以表征固体的硬度[18]，E值越大，材料的硬度就越大. 我们计算的杨氏模量为23.9 GPa，说明AsI3硬度不高. 泊松比同单向受拉或受压时所产生的体积变化密切相关，泊松比理论上限为0.5，表明弹性形变过程中体积不发生变化，具有无限大的弹性各向异性特征. 我们得出的泊松比为0.22，暗示了AsI3在弹性形变过程中具有较大的体积变化. 为了证明压缩特性，在图2中，我们给出AsI3相对晶轴比及体积随压强的变化关系. 从计算所得可看出，当压力增大到30GPa时，体积已经坍缩了48%，体系具有较强的可压缩性.

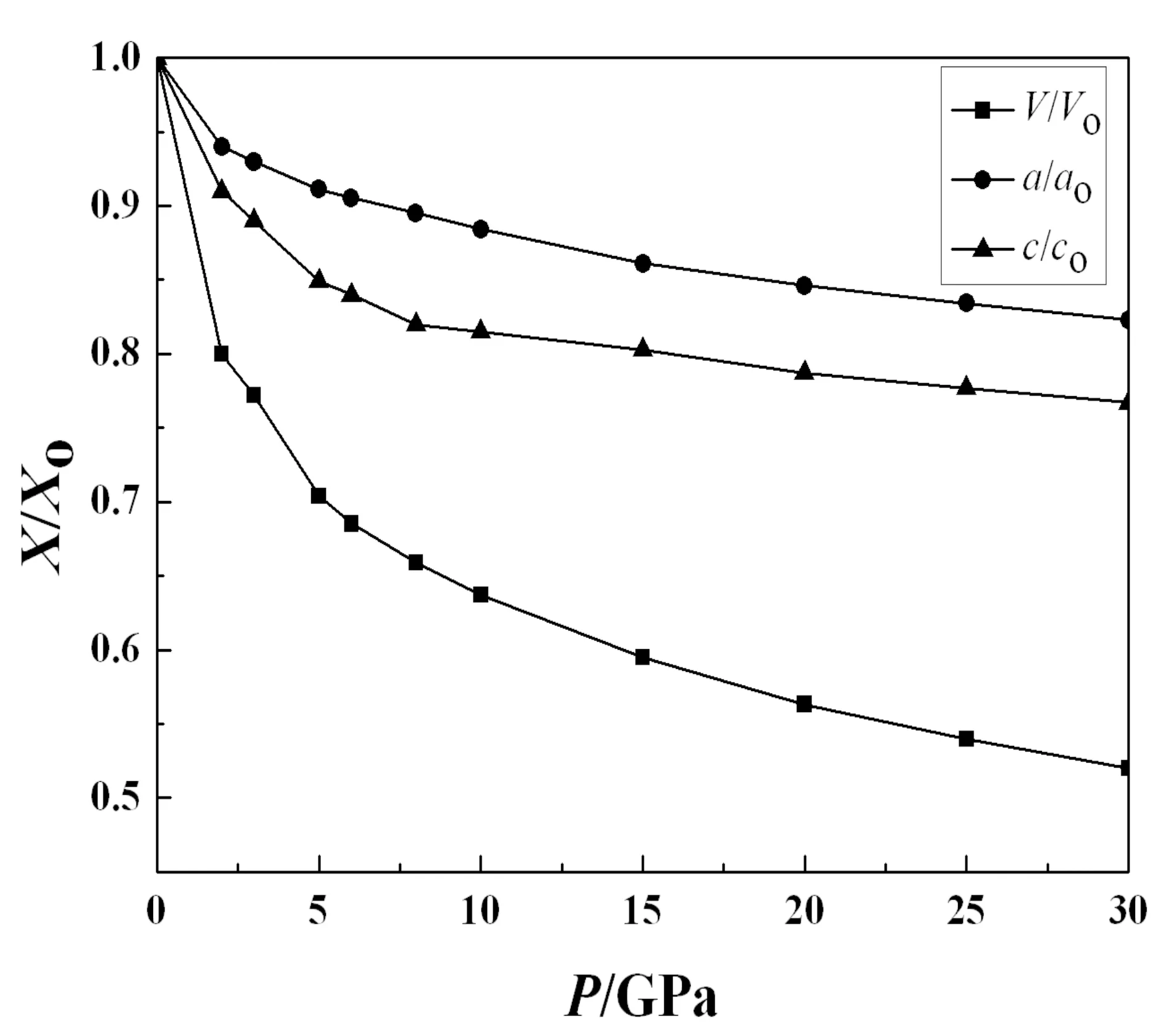
图2 AsI3相对晶轴比及体积随压力的变化关系 Fig. 2 Relative changes of lattice parameters (a and c) and volume V with pressure

此外，通过B/G比值可以分析材料的延展性. 如果B/G的值较大，固体相对较软，对于硅，B/G=1.4. 通过比较体模量和剪切模量，我们计算得到AsI3的B/G=1.45，表明这个材料是脆性材料，同时也反映了AsI3层间是由较强的范德瓦尔斯力结合.

德拜温度是晶格最高振动简正模的温度，它使固体的力学性质和热力学性质相关联，例如，熔点、比热、导热系数和晶格振动焓. 从弹性常数，我们可以计算晶体的德拜温度.

德拜温度ΘD可以由下式计算得出[19]:

(12)

其中，Vm是平均弹性波速，h是普朗克常数，NA是阿弗加德罗常数，M是分子质量，n是分子中原子的个数，ρ是密度，k是玻耳兹曼常数.

由已知的弹性模量可以计算多晶的纵的弹性波速Vl和横的弹性波速Vt.

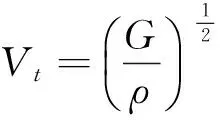
(13)

由Vl和Vt，可以计算出平均弹性波速Vm，

(14)

经过计算，Vl=1.508×103m/s，Vt=2.516×103m/s，Vm=1930 m/s，ΘD=163 K. 德拜温度可以粗略指出晶格振动中声子振动频率的数量级，德拜温度为163 K，相当于晶格振动频率的数量级为1014Hz.

分析晶体的弹性各向异性特征对于理解晶体的力学性质具有重要意义. 通常，弹性各向异性表现为剪切和压缩各向异性. 对于六角晶系，C44/C66比值反映了剪切各向异性. 对于R-3结构的AsI3，C44为10.0 GPa，C66为12.2 GPa，C44/C66=0.82，表明其稍大的剪切各向异性. 压缩各向异性可以通过分析c/a率与压力的关系得到，如图3所示. 从图3可以看出，压力小于8 GPa时，c/a值随压力的增加而减小，表明a-轴比c-轴更难压缩，这种压缩的各向异性与电子库仑排斥的各向异性相关. 最有兴趣的是，我们注意到在8 GPa左右，c/a值最小，这暗示着8 GPa左右可能存在结构相变. 此外，弹性常数的计算表明，当压力上升到4 GPa时，弹性常数不满足力学稳定条件. 因此，从晶体结构的力学角度判断，在4 GPa时AsI3的R-3相应该是亚稳结构.

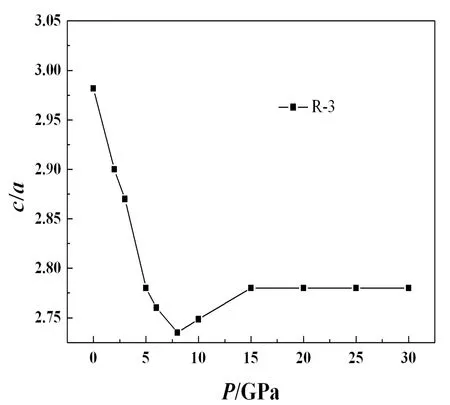
图3 AsI3的c/a比值与压力的关系Fig. 3 The c/a ratio as a function of pressure for AsI3

最近，Ranganathan和Ostioja-Starzewski[20]用弹性各向异性因子AU来表征晶体的各向异性特征.

(15)

AU=0，表示弹性局部各向同性；AU值的大小，代表单晶各向异性的程度. 我们计算得到AsI3的AU值为1.11, 这个值大大偏离零值，再次暗示了这个材料的大的弹性各向异性特征.

3.3 电子特征分析

电子性质是了解不同结构材料物理和化学性质的一个重要的手段. 为了弄清楚电子性质和力学性质之间的关系，我们计算了AsI3在零压下的电子能带、态密度和电子差分密度.

化学键的类型影响着材料的弹性性质. 由固体理论可知，具有高方向性的共价键在抵抗弹性和塑性形变上明显优于离子键或金属键. 为了更形象的阐明AsI3的化学键的性质，在图4中画出了R-3结构的(1 1 1) 晶面的差分电荷密度图. 图中可以清楚的看出，电荷密度平面中没有明显的电荷集中，As和I原子之间没有明显的轨道杂化，在原子周围电荷分布较弱的重叠，因此As原子和I原子之间存在较弱的共价化学键. 我们也观察到，I原子附近的电荷密度明显大于As原子，因此As原子和I原子之间存在电荷转移，I原子得到电子而As原子失去电子，这是典型的离子键特征. 通过Mulliken电子布居的分析也可以看出AsI3的这种离子特性. 计算表明As原子带正电荷(+0.24 e)，I原子带负电荷(-0.08 e)，As原子失去电子而I原子得到电子，说明As和I原子之间存在明显的离子键. AsI3是层状结构的晶体，层内原子由离子键结合，使AsI3具有较小的块体模量，因此AsI3晶体有较强的可压缩性. 另外，我们也注意到，层间沿c-轴方向As-I原子之间的键长是3.406 Å，而层内的键长是2.608 Å. 典型的层状结构和大的原子间距暗示了原子间弱的相互作用，电子密度沿着ab-平面方向强于c-轴方向，致使沿a-轴或b-轴比c-轴方向具有更强的电子排斥作用. 因此，低压下a-轴或b-轴比c-轴方向有更强的不可压缩性，这和我们在图3中分析的结果一致.

图4 R-3结构的AsI3 (1 1 1) 晶面的差分电荷密度Fig. 4 The charge density distribution for the R-3 phase of AsI3 in (1 1 1) plane

R-3结构在零压下的能带如图5所示. 从图5可以看出，AsI3是间接带隙半导体，零压下的带隙是2.34 eV. R-3结构的带隙随着压力的增加而减小，如图6所示. AsI3在零压下的总态密度和原子的各分波态密度被绘于图7中. 对于R-3结构，靠近费米能级的导带部分主要来源于As-p和I-p态的贡献. 价带基本上可以分为3个区域：-14 eV到-9 eV主要是来自s轨道贡献；-4 eV到-2 eV主要是p轨道的贡献；价带顶附近(-2 eV-0 eV)主要由I-p和少量As-s轨道贡献，它们之间存在弱的轨道杂化，故As-I 原子之间有较弱的共价键，这种原子间弱的相互作用使得晶体具有小的块体模量. 因此，As和I之间的化学键应该是共价键和离子键的混合. 共价键的存在，有助于AsI3对抗压缩，使AsI3具有较大的硬度.

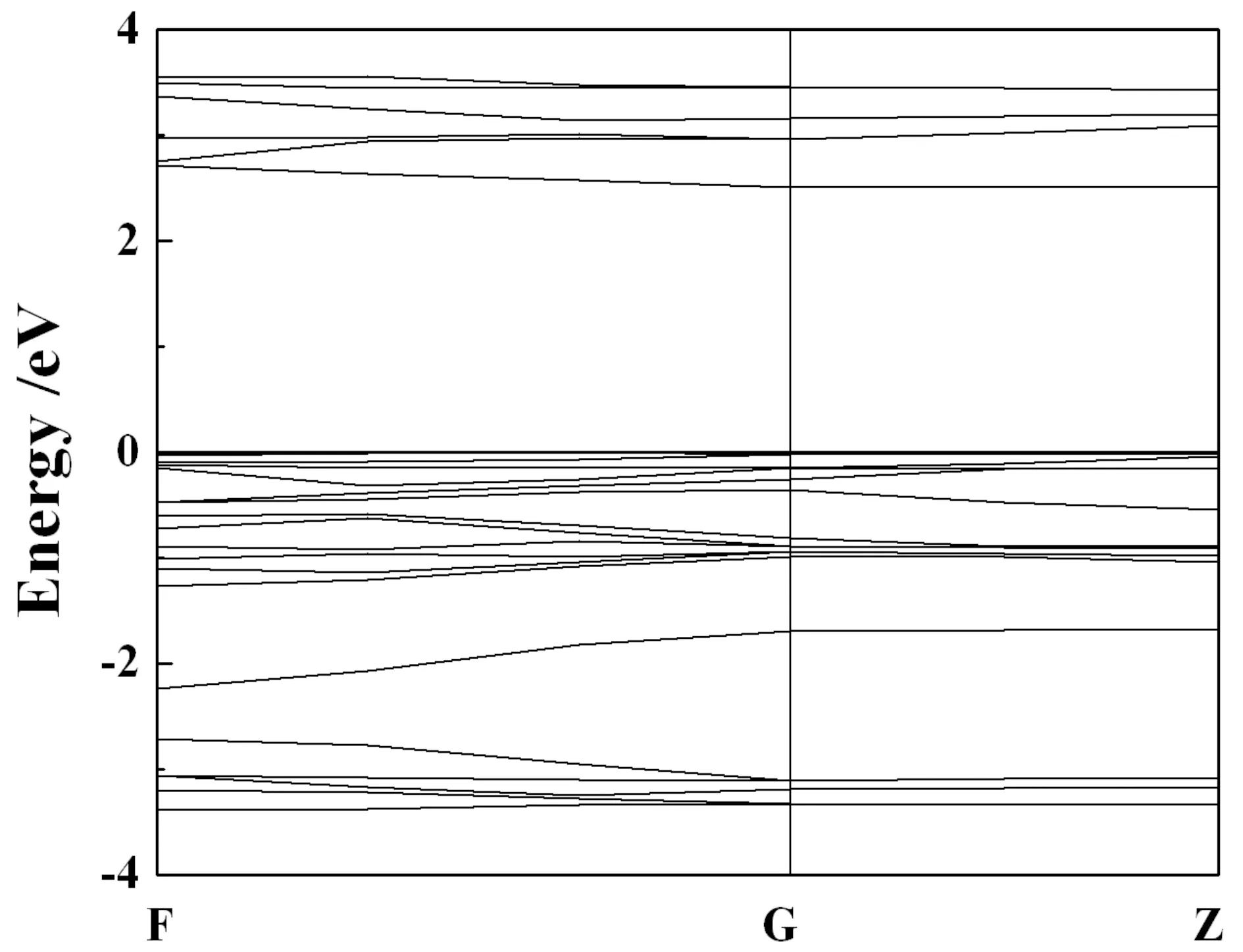
图5 零压下AsI3的能带Fig. 5 Electronic band structure for AsI3 at zero pressure

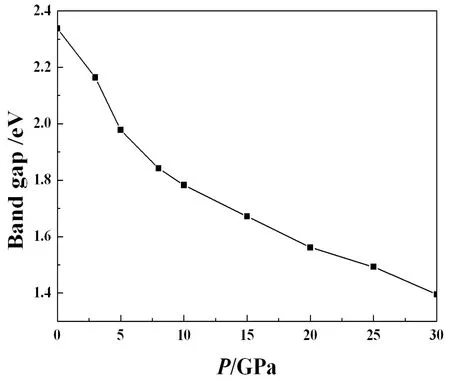
图6 带隙和压力的关系Fig. 6 Change of band gap with increasing pressure

4 结 论

利用基于密度泛函理论的第一性原理方法研究了半导体材料AsI3的结构、力学和电子学性质. 我们的主要结果如下：

1.常压下的稳定结构是R-3结构，优化得到的平衡结构参数和实验值符合的很好.

2.常压下，AsI3具有较弱的不可压缩性，这主要是由于AsI3结构中原子间弱的相互作用导致的. 大的剪切和压缩各向异性使AsI3晶体具有大的弹性各向异性特征. 泊松比计算表明AsI3是脆性材料，硬度较小.

3.对R-3结构AsI3的差分电荷密度分析表明，AsI3的化学键应该是弱共价键、离子键二者的混合. 电子能带和态密度的计算结果表明，R-3结构是间接带隙半导体，零压下R-3结构的带隙是2.34 eV，带隙随着压力的增加而减小.

[1] Sun X X, Wu C L, Chen W W,etal. Structural and elastic properties of antimony triiodide from first-principles calculations [C].AdvancedMaterialsResearch, 2013, 750-752: 1782.

[2] Sun X X, Ren Z R, Wang D G. Structural transitions of BiI3under pressure [J].ModernPhysicsLettersB, 2012, 26 (32): 1250217.

[3] Sun X X, Li Y L, Zhong G H,etal. The structural, elastic and electronic properties of BiI3: First-principles calculations [J].Phys. B, 2012, 407: 735.

[4] Madson W H, Krauskopf F C. A study of the preparation and certain properties of arsenic tri-iodide [J].Recl.Trav.Chim.Pays-Bas, 1931, 50: 1005.

[5] Anderson A, Campbell J A, Syme R W G. Raman spectra of crystalline antimony triiodide and arsenic triiodide [J].JournalofRamanSpectroscopy, 1988, 19(6): 379.

[6] Virko S, Petrenko T, Yaremko A,etal. Density functional and ab initio studies of the molecular structures and vibrational spectra of metal triiodides, MI3(M=As, Sb, Bi) [J].JournalofMolecularStructure:Theochem, 2002, 582 (1): 137.

[7] Trotter J. The crystal structure of arsenic triiodide, AsI3[J].ZeitschriftfuerKristallographie, 1965, 121: 81.

[8] Anderson A, Sharma S K, Wang Z. Raman study of arsenic tri-iodide at high pressures [J].HighPressureResearch, 1996, 15(1): 43.

[9] Saitoh A, Komatsu T, Karasawa T. Raman scattering under hydrostatic pressure in layered AsI3crystals [J].Phys.StatusSolidiB, 2000, 221: 573.

[10] Segall M D, Lindan P J D, Probert M J. First principles simulation: ideas, illustrations and the CASTEP code [J].JournalofPhysical:CondensedMatter, 2002, 14 (11): 2717.

[11] Ihm J, Zunger A, Cohen M L. Momentum-space formalism for the total energy of Solids [J].J.Phys. C:SolidStatePhys., 1979, 12 (21): 4409.

[12] Vanderbilt D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism [J].Phys.Rev. B, 1990, 41 (11): 7892.

[13] Perdew J P, Burke K, Ernzerhof M. Generalized gradient approximation made simple [J].Phys.Rev.Lett., 1996, 77 (18): 3865.

[14] Hill R. The elastic behaviour of a crystalline aggregate [J].Proc.Phys.Soc. A, 1952, 65(5): 349.

[15] Hsueh H C, Chen R K, Vass H,etal. Compression mechanics in quasimolecular XI3(X= As, Sb, Bi) solids [J].Phys.Rev. B, 1998, 58 (22): 14812.

[16] Ravindran P, Fast L, Korzhavvi P A,etal. Density functional theory for calculation of elastic properties of orthorhombic crystals: Application to TiSi2[J].J.Appl.Phys., 1998, 84 (9): 4891.

[17] Born M, Huang K.Dynamicaltheoryofcrystallattices[M]. Oxford: Clarendon Press, 1968.

[18] Mattesini M, Ahuja R, Johansson B. Cubic Hf3N4and Zr3N4: a class of hard materials [J].Phys.Rev. B, 2003, 68 (18): 184108.

[19] Anderson O L. A simplified method for calculating the Debye temperature from elastic constants [J].J.Phys.Chem.Solids, 1963, 24 (7): 909.

[20] Ranganathan S I, Ostoja Starzewski M. Universal elastic anisotropy index [J].Phys.Rev.Lett., 2008, 101(5): 05504.

The electronic structure and elastic properties of AsI3: first-principles calculations

SUN Xiao-Xiao1, LI Min-Jun1, ZHAO Xiang-Min1, CHEN Yu-Qiang1, LI Cong2

(1.School of Engineering, Mudanjiang Normal University, Mudanjiang 157012, China;2.School of Science, Mndanjiang Normal University, Mudanjiang 157012, China)

We employ first-principles pseudopotential method based on density functional theory to investigate the equilibrium lattice parameters, elastic and electronic properties of AsI3. The calculated results indicate that the rhombohedral R-3 structure of AsI3is stable at zero pressure and the equilibrium structural parameters agree well with the experimental values. For AsI3, the calculated bulk modulus, shear modulus, and the Young’s modulus are 14.2 GPa, 9.8 GPa, and 23.9 GPa, respectively. The Poisson’s ratio is 0.22 and the Debye temperature is 163 K. AsI3presents larger elastic anisotropy, better ductility and stronger compressibility. The calculations of band structure show that AsI3is an indirect band-gap semiconductor with band gap (～2.34 eV). The analysis of the charge density distribution demonstrates that AsI3is of the mixtures of weak covalent and ionic bonds.

AsI3; Anisotropy; First principles; Electronic properties

2014-11-08

黑龙江省教育厅科学技术研究项目资助(12543080)

孙霄霄(1979—),女，副教授，主要从事计算材料科学方面的研究. E-mail: am1979@126.com

103969/j.issn.1000-0364.2015.10.027

O472

A

1000-0364(2015)05-0879-06