电磁诱导光透明过程中两原子的自旋极化特性

2015-03-23李敏,郑丽,付静

原子与分子物理学报 2015年5期

李敏, 郑丽, 付静

(1. 集美大学诚毅学院, 厦门 351100; 2. 大连工业大学信息科学与工程学院, 大连 116034; 3.吉林建筑大学城建学院，长春 130111)

李敏1, 郑丽2, 付静3

(1. 集美大学诚毅学院, 厦门 351100; 2. 大连工业大学信息科学与工程学院, 大连 116034; 3.吉林建筑大学城建学院，长春 130111)

本文研究了电磁诱导光透明过程中两原子的自旋极化矢量.对于数态探测场，在光信息转移过程中，两原子自旋极化矢量始终固定在z方向，大小变化非常明显，两原子一般处于混合态；对于相干态探测场，自旋极化矢量大小变化很微弱，两量子比特基本处于纯态，这有利于改善系综内原子之间的相干性，但自旋极化矢量的方向在x-z平面内.

电磁诱导光透明; 自旋极化矢量; 平均自旋; 相干性

1 引言

在研究自旋压缩的时候，为了能找到最小的自旋涨落度量压缩，必须先确定自旋极化矢量[1-3]，大小和方向都是依赖于自旋的三分量的平均值[4-6].对于单个量子比特，自旋极化矢量的大小不仅仅是其状态混合程度的度量，也是其信息量的度量[7]；在多粒子自旋体系中，一般地，粒子之间的线性相互作用，不会引起极化矢量大小的变化，体系是不产生自旋压缩的，从而使体系始终保持在自旋相干态上；但如果粒子之间有非线性相互作用，那么，体系极化矢量大小和方向都可能会发生变化，从而产生自旋的压缩和量子纠缠.

在量子信息领域中，光场是非常好的信息载体，通过与原子系综的相互作用，利用电磁诱导光透明(EIT)机制[8-10]，可以绝热地将探测场的光信息存储在原子系综内，也可以将其再释放出来.从量子态的观点来看，就是利用暗态的概念，再结合控制光，让探测光-原子系综复合系统在两个量子态之间绝热地转换.物理上，当两束光强度形成鲜明的对比的情况下，微弱的探测场不能让系综内的原子激发，强度弱的探测光则会畅通无阻的漏过介质[11-14]，实现介质对探测光的透明现象.当然，通过绝热地调节控制光，提升探测场的强度，探测场会与原子发生相互作用，光子消失，激发原子，从而实现光信息向原子系综的存储.

本文中，针对上述的量子信息存储方案，在量子信息转换的过程中，对不同的探测场，讨论控制光场变化时，原子系综双原子自旋极化矢量的变化.

2 电磁诱导光透明过程

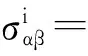
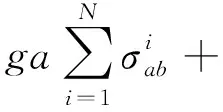
(1)

其中，a是量子场的湮灭算符，g为耦合强度，如果满足大N极限与低激发条件，那么，只有少数的原子占据|a>或|c>，通过计算，该哈密顿量有一个本征值为零的退化家族[14-16].

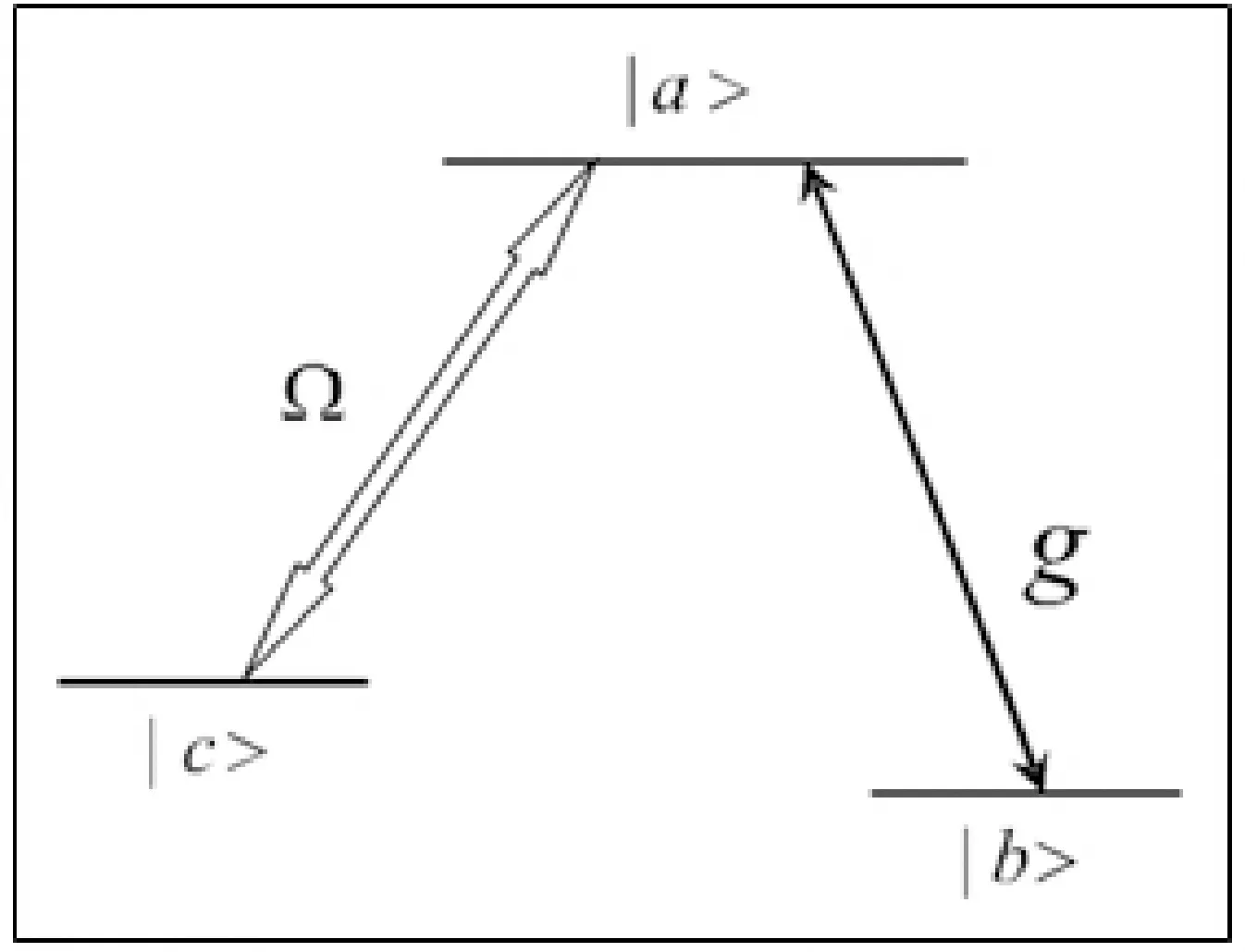
图1 λ型三能级原子与量子场和经典场耦合Fig.1 λ-type three-level atom coupling with quantum field and classical field

为了实现量子记忆过程的描述，引入暗态极化子的概念[14]，

|dn>=(n!)-1/2D+n|0>

(2)

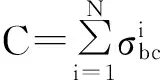
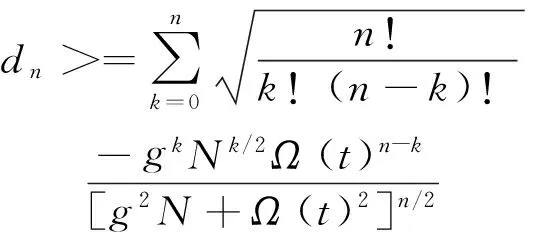
(3)

3 两原子自旋极化矢量的计算

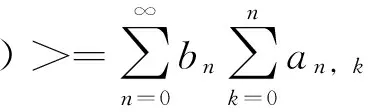
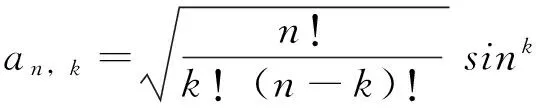
(4)

其中sin[θ(t)]=-gN1/2/[g2N+Ω(t)2]1/2，cosθ(t)=Ω(t)/[g2N+Ω(t)2]1/2，通过求迹运算，可以得到原子系综的状态，通常，该态是混合态，即

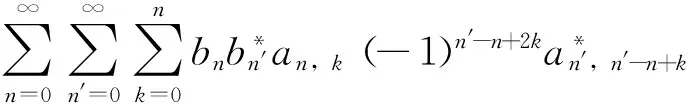
(5)

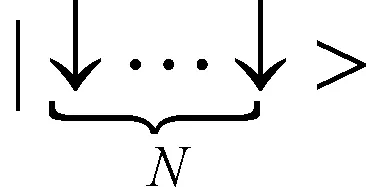
在四个基底|00>，|01>，|10>和|11>下，两原子的状态可以由下列密度矩阵给出

(6)

各个矩阵元可表示为[15,16]

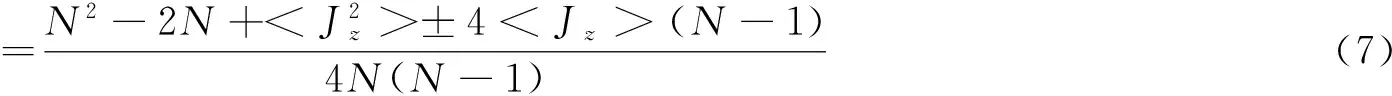
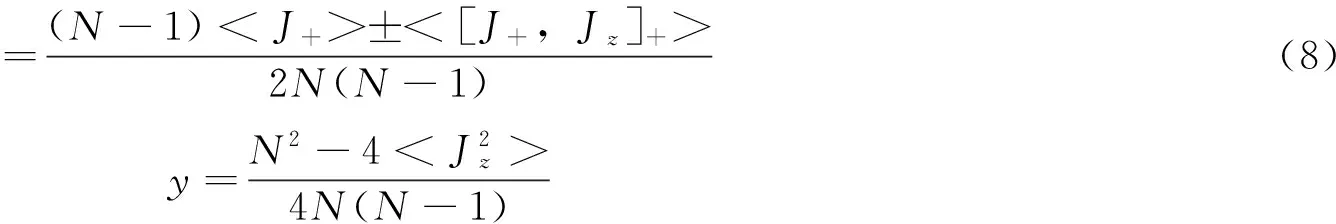
式中Jz，J+是描述N个原子的集体自旋算符，考虑到两原子的集体自旋算符

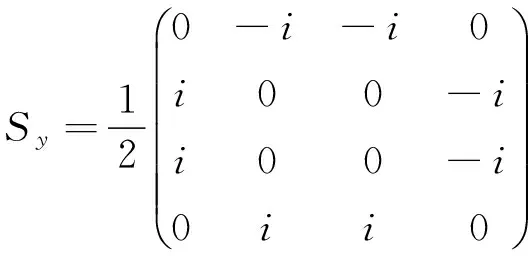
通过计算可得到三个算符的期望值

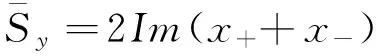
那么，自旋极化矢量大小可以表示为

而方向，则可以用三个方向余弦来表示

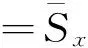
(13)

4 两原子自旋极化矢量的讨论

4.1 数态探测场信息转移过程中两原子自旋极化矢量

通过计算，很容易得到量子态ρA和ρij可变为

ρA=trF(|ψ(θ)><ψ(θ)|)=

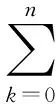
(14)

进一步可得到期待值

=0, =0, =v+-v-

(16)

4.2 相干态探测场信息转移过程中两原子自旋极化矢量

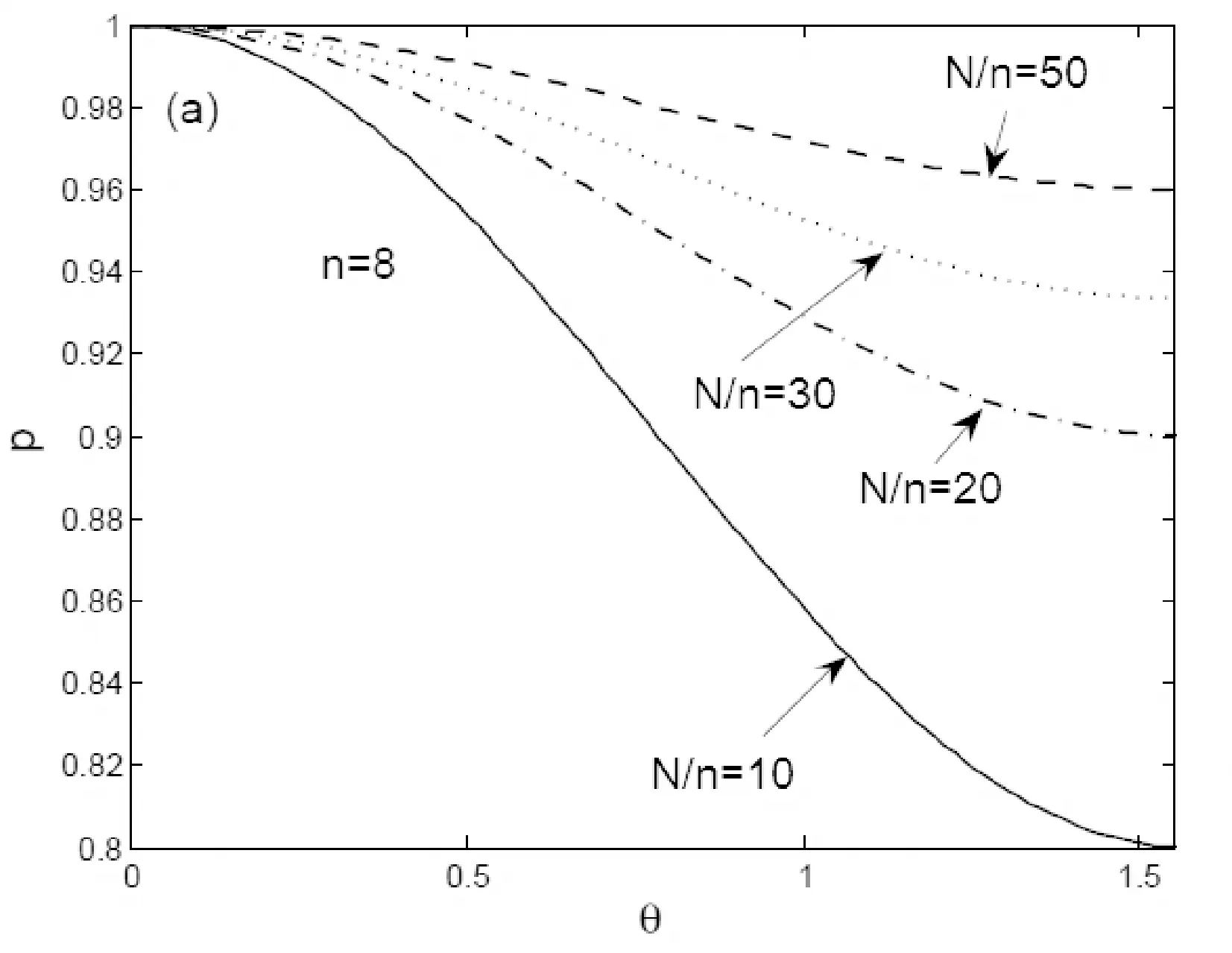
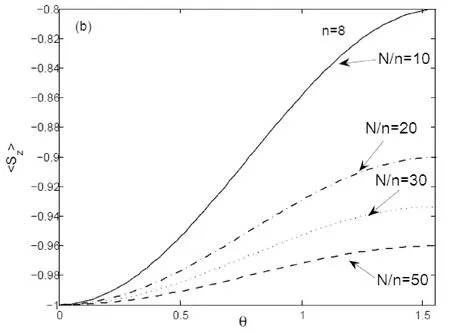
图2 光子数n取8时，自旋极化矢量p及自旋平均值在信息转移过程中随角度θ的变化Fig.2 The spin polarization and the expectation value of spin as functions of θ when photon number equals to 8

如果相干态|α>作为探测场，为方便起见，平均光子数在这里记为|α|2，我们同样考察了自旋极化矢量随角度的变化.比较于数态光场的情况，发现自旋极化矢量只是细微地发生变化，如图3(a)和图2(a)中相应曲线比较所示.这表明在探测场信息向原子系综转移的过程中，两原子之间的相干性有了本质的改善，在比值|α|2/N比较大的情况下，它们的状态非常接近纯态.从物理上来看，原子间的相干性得到了很好的保持，这得益于探测场是相干场，光信息转移时，原子系综只是从自旋极化矢量在z方向的自旋相干态，变化到另一个相干态.进一步，我们考察了两原子三个自旋分量的平均值，发现这时的平均自旋在x-z平面内.比值|α|2/N越小，原子系综最后的自旋极化矢量越接近x方向；反之，比值越大，自旋极化矢量越接近z方向，如图3(b)两分量比较所示.另外，在|α|2/N一定的情况下，平均光子数对自旋极化矢量也有影响，|α|2越大，自旋极化矢量变化越明显，这与数态探测场情况下自旋极化矢量的行为是不同的，如图3(c)中三线比较所示.这表明，探测场越强，在完成信息转移时，要保持系综内原子自旋之间的相干性，需要更多的原子数目.

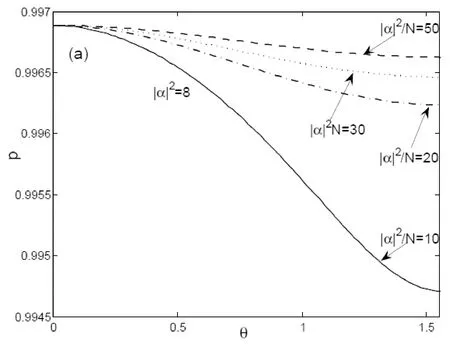
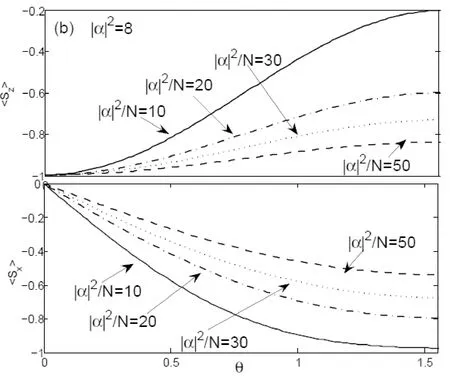
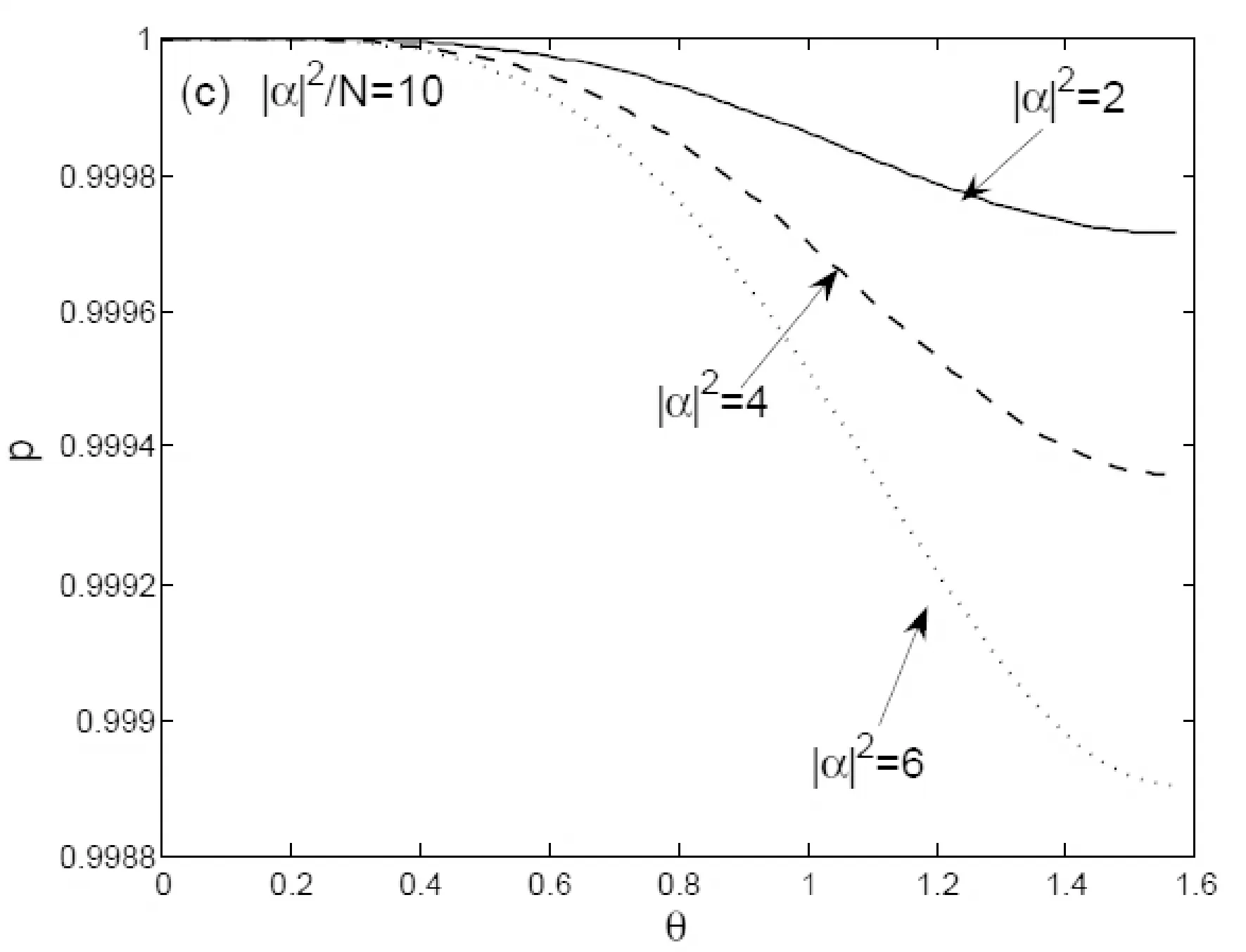
图3 自旋极化矢量p及自旋分量平均值在不同条件下随角度θ的变化Fig.3 The spin polarization and the expectation value of spin components as functions of θ for the different parameters

5 结论

本文研究了电磁诱导光透明过程中，系综内两个原子之间的自旋极化矢量，通过研究，结论如下：

(1)探测场如果是光子数态，那么,自旋极化矢量变化比较明显，这依赖于光子数与原子数目的比值，两原子通常处于混合态，但平均自旋在z方向.

(2)探测场如果是相干光场，自旋极化矢量变化很微弱.比较与前者，原子之间的相干性有根本的改善，在信息转移过程中，原子可以保持在自旋相干态上，但平均自旋在x-z平面内.

(3)从结果来看，通过相干光场，利用电磁诱导光透明机制，不能够生成自旋压缩态和自旋纠缠态，如果要生成自旋压缩态，则必须要改变探测场的类型.

[1]KitagawaM,UedaM.Squeezedspinstates[J]. Phys. Rev.A, 1993, 47(6): 5138.

[2]JinGR,KimSW.Spinsqueezingandmaximal-squeezingtime[J]. Phys. Rev.A, 2007, 76(4): 043621.

[3]JinGR,KimSW.Storageofspinsqueezinginatwo-componentBose-Einsteincondensate[J]. Phys. Rev. Lett., 2007, 99(17): 170405.

[4]WangXG,SandersBC.Spinsqueezingandpairwiseentanglementforsymmetricmultiqubitstates[J]. Phys. Rev.A, 2003, 68(1): 012101.

[5]YanD,WangXG,WuLA.Squeezingintherealandimaginaryspincoherentstates[J]. Chin. Phys. Lett., 2005, 22(3): 521.

[6]YanD,WangXG,SongLJ, et al.Meanspindirectionandspinsqueezinginsuperpositionsofspincoherentstates[J]. Cent. Eur. J. Phys., 2007, 5(3): 367.

[7]DavideG,TommasoT,GerardoA.Characterizingnonclassicalcorrelationsvialocalquantumuncertainty[J]. Phys. Rev. Lett., 2013, 110(3): 240402.

[8]HarrisSE,FieldJE,KasapiA.Dispersivepropertiesofelectromagneticallyinducedtransparency[J]. Phys. Rev.A, 1992, 46(1): 29.

[9]HarrisSE.Electromagneticallyinducedtransparency[J]. Phys. Today, 1997, 50: 36.

[10]LezamaA,BarreiroS,AkulshinAM.Electromagneticallyinducedabsorption[J]. Phys. Rev.A, 1999, 59(6): 4732.

[11]MattiasJ,KlausM.Storingquantuminformationinasolidusingdark-statepolaritons[J]. Phys. Rev.A, 2004, 70(3): 032320.

[12]SchoriC,JulsgaardB,SoensenJL, et al.Recordingquantumpropertiesoflightinlong-livedatomicspinstate:Towardquantummemory[J]. Phys. Rev. Lett., 2002, 89(5): 057903.

[13]LukinMD,YelinSF,FleischhauerM.Entanglementofatomicensenmblebytraappingcorrelatedphotonstates[J]. Phys.Rev. Lett., 2000, 84(18): 4232.

[14]FleischhauerM,LukinMD.Dark-statepolaritionsinelectromagneticallyinducedtransparency[J]. Phys. Rev. Lett., 2000, 84(22): 5094.

[15]SunCP,LiY,LiuXF.Quasi-spin-wavequantummemorieswithadynamicalsymmetry[J]. Phys. Rev. Lett., 2003, 91(14): 147903.

[16]WangXG,MolmerK.Pairwiseentanglementinsymmetricmulti-qubitsystems[J]. Eur. Phys. J.D, 2002, 18(10): 385.

Spin polarization of twoatoms of the system with the electromagnetically induced transparency

LI Min1, ZHENG Li2, FU Jing3

(1.Chengyi College, Jimei University, Xiamen 351100, China; 2.School of Information Science and Engineering, Dalian Polytechnic University,
Dalian 116034, China; 3.The City College of Jilin Architectural and Civil Engineering University, Changchun 130111, China)

We investigate spin polarization of two atoms in process of information transfer between probe field and atomic ensemble in the electromagnetically induced transparency. For the number state of the probe light, the mean spin of two atoms is always in thezdirection, and as the strength of the driving field increases, it changes obviously. However, for the coherent state of the probe light, the mean spin changes weakly in thex-zplane. Due to the coherent state, the two atoms stay in the pure state almost, and the coherent between the atoms can be improved obviously.

Electromagnetically induced transparency； Polar vector； Average pin； Coherence

国家自然科学基金(116034); 福建省中青年教师教育科研项目(JB14219)

李敏(1980—)，女, 福建厦门人, 硕士, 讲师, 主要从事量子信息的研究.E-mail: kelly.limin@163.com

付静.E-mail: 63387187@qq.com

103969/j.issn.1000-0364.2015.10.021

0431.2

1000-0364(2015)05-0848-05

投稿日期:2015-01-10