HOF分子电离态的运动方程耦合簇研究

陈恒杰， 郭 雷, 方 旺, 刘丰奎

(1.重庆科技学院数理学院， 重庆 401331; 2. 重庆大学化学化工学院， 重庆 400044)

HOF分子电离态的运动方程耦合簇研究

陈恒杰1， 郭 雷2, 方 旺1, 刘丰奎1

(1.重庆科技学院数理学院， 重庆 401331; 2. 重庆大学化学化工学院， 重庆 400044)

采用单双激发运动方程耦合簇(EOM-CCSD)以及多个包含迭代三激发在内的运动方程耦合簇变体(EOM-CCSDT-i,i=1a,1b,2,3和EOM-CC3)计算了HOF价层垂直电离势(VIP). 在EOM-CCSD水平上优化出各价层电离态结构, 得到绝热电离势(AIP), 进一步计算出谐振频率. 同时对称匹配簇组态相互作用(SAC/SAC-CI)也被应用到部分计算. 结果显示：EOM-CC3、EOM-CCSDT-3计算的VIP接近于全三激发运动方程耦合簇EOM-CCSDT结果; EOM-CC与SAC-CI值基本一致; 同时发现HOF光电子能谱实验在2A′态指认上有误并重新进行归属. HOF的第三VIP应为16.9 eV, 而非光电子能谱实验测得的16.0 eV.

HOF; 运动方程耦合簇; 对称匹配簇组态相互作用; 外价层电离势

1 引 言

活性卤素化合物HOF是大气化学中一个重要的反应中间体, 其可与臭氧反应而对环境有一定破坏作用[1]. 因此对其电离、激发过程研究十分重要. Kim等最早用微波谱、从头算结合旋振光谱数据等方法决定出HOF的分子结构[2-5]. 然而由于HOF的瞬态特性、合成和提纯困难等原因, 对HOF电离态的研究依然非常少, 截至目前关于HOF电离态的实验文献仅有两篇. Berkowitz用光电离质谱测出HOF的第一绝热电离势为12.71 eV[6], 同时他们也用He I光记录了HOF直到21.2 eV的光电子能谱, 三个价带被发现, 相应的垂直电离势和绝热电离势一并被估计[7]. 结合从头算五个价层电离峰依次被归属到A″、A′、A′、A″和A′′对称性. 理论方面, Chong用微扰关联的Koopmans理论[8]、Alti等用MS-Xα方法[9]、Dceleva用2h-1p方法[10]以及Hu等用GW2方法[11]对HOF的价层垂直电离势(VIP)进行了计算. 上述理论方法在早期电离态研究中发挥了重要作用, 但其结果是非常粗糙的, 很难定量和系统的描述分子电离势.

耦合簇方法(CC)已被广泛应用到中小尺度分子的基态计算, 运动方程耦合簇(EOM-CC)也被扩展到处理电离态. 我们曾对XF3(X=N,P,As)的电离态进行单双激发运动方程耦合簇(EOM-CCSD)计算[12], 当时即未考虑三激发的贡献, 也仅仅针对VIP, 没有考察电离态结构、谐振频率和AIP. 本文主要利用包含三激发贡献的多种EOM-CC变体对HOF电离态进行系统计算, 准确描述该分子基态结构、VIP, 同时用EOM-CCSD优化出电离态结构, 给出了绝热电离势(AIP), 结合理论分析对HOF光电子能谱存在的问题进行了探讨.

2 计算方法

首先进行闭壳层Hartree-Fock(HF)自洽场(SCF)计算, 关联能通过耦合簇方法(CC)处理. 接着采用CCSD、CCSDT-3、CC3、CCSDT 结合解析梯度方法优化出基态几何结构, 优化时耦合簇能收敛标准为10-8Hartree, 几何收敛标准为直到前后两次结构的均方根(RMS)梯度小于10-7Hartree/Bohr. 在优化出的结构上, 利用解析二阶导数法获得谐振频率. 利用EOM-CCSD、EOM-CCSDT-i(i=1a,1b,2,3)、EOM-CC3和EOM-CCSDT计算价层垂直电离势时, 先获得基态能, 然后从对应轨道上移除一电子, 应用运动方程(EOM)法得到其电离态能量. 电离态结构优化采用解析梯度方式的EOM-CCSD方法, 所有优化参数与基态相同. 为了比较这里也应用 SAC/SAC-CI方法进行计算, 基态、电离态结构优化以及绝热电离势计算采用单双激发的SD-R模式, 垂直电离势计算还包含有三激发贡献的General-R(N=3)模式, SAC-CI只能采用数值梯度优化.

CC计算时所有电子被包括到关联能计算中, SAC-CI计算仅包括价电子. 所有计算采用Dunning的相关一致aug-cc-pVTZ基组. CC和EOM-CC计算由CFOUR程序包[13]完成, SAC-CI使用Gaussian程序[14].

3 结果与讨论

3.1 基态结构

在Cs对称性下, 对HOF分子基态X1A′进行结构优化, 结果见表1. 可以看出, 包含三激发贡献的CCSD(T)、CC3、CCSDT-3和CCSDT优化的键长均保持在ROH=0.967 Å、ROF=1.437 Å和θ=97.8°左右, 与实验值差异仅约0.2%. CCSD计算的键长略小于、键角轻微大于上述理论值. 优化时包含全部三激发贡献的耦合簇方法CCSDT所需计算资源和机时要远大于CC3、CCSDT-3, 但结果并没有显著改善, CCSDT-3计算的ROH值与CCSDT结果完全一致,ROF仅有0.001Å的差异,θ值相对差异则更小, 说明CCSDT-3包含了绝大多数对关联能有贡献的三激发. 因为CCSDT-3已十分接近理想的包含全三激发贡献的CCSDT, 在计算资源缺乏的情况下, 可用CCSDT-3代替CCSDT计算, 这样可在损失精度非常小的情况下大大节约计算资源、提高计算速度. 多种包含三激发的CC中, CCSD(T)计算速度相对最快. 键长ROH远小于ROF, 说明OH键能比OF大, 其稳定性要强于OF, 表现在波函数中OH键电子云重叠大于OF. 由此推断, 在θ不变情况下, 解离时OF所需能量要小于HO, HOF会率先解离成HO自由基和F离子, 表现在解离曲线上是OF的能垒低于HO. 关于谐性频率, 由表1知, 除CCSD给出的结果与实验值917、1396和3764 cm-1差距较大外, CCSD(T)、CC3和CCSDT-3均能给出十分精确的谐振频率值. 值得注意的是, 大多实验上往往给出的是基频而非谐频, 若直接把CC谐频结果与实验基频值进行比较, 结果必然存在较大差异, 而基频需通过非谐性分析获得, 这将在后续工作中进行研究.

利用SAC方法优化得到的HOF基态结构也列于表1. SAC优化的结构与CCSD十分相近, 这是因为理论上未约化的SAC与CCSD是等价的, 原则上SAC/SAC-CI能利用数值梯度计算谐振频率, 只需手动写入多个构型点. 然而实际计算显示, 这种方法在效率、精度等方面都存在问题, 因此后文的电离态计算也仅用SAC-CI优化结构, 未给出谐性频率.

3.2 垂直电离势

基态结构优化表明HOF的基电子组态为：

(1a′)2(2a′)2(3a′)2(4a′)2(5a′)2(1a″)2(6a′)2(7a′)2(2a″)2

轨道成份分析分析显示：2a″为O原子和F原子2p轨道形成的反键π轨道, 这与光电子能谱实验和半经验解释一致[7]. 7a′则是由F原子和O原子2p轨道上的孤对电子构成的非键轨道, Lewis结构理论也显示在O、F原子上分别存在两个和三个孤电子对. 6a′是O和F原子轨道在轴向上相互作用而形成的σ分子轨道, 1a″为2a″对应的成键轨道, 5a′轨道是由F、O原子的s、p轨道混合而成的弱键.

在基态结构上, 应用运动方程耦合簇EOM-CC(2)、EOM-CCSD、EOM-CCSDT-i(i=1a,1b,2,3)和EOM-CC3计算出HOF的五个价层垂直电离势, 同时应用CCSD(T)和CCSDT获得第一个2A″和2A′态的垂直电离势值, 结果见表2. SAC-CI两种激发模式下的结果、文献值和实验结果被一并列入. 从表看出, 早期的理论结果与实验值相差较大, 特别是CI计算的电离势与实验值差距多达2-3eV,扩展的Koopmans理论、pGW2和GA在精度上虽然有所提高, 但在价态仍有较大差距, 总体上EOM-CC给出的结果与实验值差异最小. 另外, 电离势计算对结构敏感的分子体系, 早期理论只能选择实验结构, 而EOM-CC方法则可在CC优化结构上进行而不依靠任何其它选择参数, 因此可以做到彻底的从头算, 进而消除结构带来的随机误差. 从结果来看, EOM-CCSD(2)与EOM-CCSD值非常接近, 最大差距不超过0.1 eV, SAC-CI的SD-R模式与EOM-CCSD结果基本一致, 说明SD-R中略去的双激发算符对价电离峰位置影响确实不大, General-R与SD-R结果相近则说明三激发对单电子电离引起的电离主峰贡献较小. 需要提出的是在计算shake-up态时, 这些未选入目前计算的算符可能有重要影响. 对于EOM-CCSD和SAC-CI由于两种方法使用的活性空间不同, 且活性空间中最终选入计算的算符也存在差异, 加上各自优化的结构也不完全相同, 使得SAC-CI与EOM-CC之间存在轻微的差异, 这是可以理解的. EOM-CC3、EOM-CCSDT-3和EOM-CCSDT结果相近且更加接近实验值, 但相对EOM-CCSD而言, 并没有大幅度减小与实验值差距, 说明大多数的双电子激发项对电离势贡献很小, 这与上述SAC-CI结论一致. 从计算过程来看, EOM-CC3、EOM-CCSDT-3需要比EOM-CCSD更大的计算资源和更漫长的计算时间, EOM-CCSDT更甚, 因此建议在计算大分子、或双电子激发项不重要的体系时可以选择EOM-CCSD, 对小分子体系或需要高精度电离势值时, 可采用EOM-CC3或EOM-CCSDT-3方法. 由表也可看出, EOM-CCSDT-i(i=1a,1b,2)值均大于EOM-CCSD和EOM-CC3, 原因有二：一是这些方法本身为激发态计算而做的近似, 电离势计算在理论上存在天然缺陷; 二, 这些计算我们未使用相应方法优化的基态结构, 而直接应用实验结构, 将会出现一些随机误差.

Berkowitz应用光电子能谱实验结合从头算指出HOF的电离态对称性依次为A″、A′、A′、A″和A′, 目前计算结果显示, 电离态对称性顺序应为A″、A′、A″、A′和A′, 我们的结果与文献[13]、[15-17]结果一致. 造成这一错误的原因可能是, Berkowitz计算时仅简单的按照基态轨道顺序对电离态进行了归属, 未考虑初态和末态弛豫效应以及电子关联效应, 而实际从任意轨道上电离一电子后, 经过一弛豫时间, 电子可能重新排布, 造成电子间的相互作用发生改变, 导致电离势与HF轨道能有所差异, 甚至电离顺序发生改变. 对HOF而言, 6a′和5a′有强烈的相互作用, 导致6a′能级下移而落后于1a″电离, 这点可从单激发组态结果得到印证, 对2a″、7a′、1a″轨道对应的电离, 其单电子电离系数均在0.9以上, 而17.83、19.69 eV对应的电离峰则由5a′和6a′共同构成, 其中17.83 eV的电离系数为0.81, -0.46, 19.69 eV电离峰为0.82, 0.49.

光电子能谱实验结果显示, 在12.69、14.50和16.00 eV处发现有三个电离主峰, 然而EOM-CC、SAC-CI结果支持前两个峰, 对第三个电离峰16.00 eV,EOM-CC和SAC-CI结果均显示该峰出现在16.9 eV左右, 应用多种方法计算的早期文献结果也与目前结果一致. 产生这个问题无外乎以下原因, 光电子能谱实验指认有误或者前文描述的所有垂直电离势计算方法均存在问题, 后者显然是不可能的. 大量文献和计算经验也显示, 在外价层光电离主峰位置, EOM-CC和SAC-CI计算值与实验值差距高达0.9 eV是不可能出现的事情, 遗憾的是光电子能谱实验文献也仅在表中列出该峰粗略的估值, 并未给出其谱图. 结合目前计算, 我们认为HOF的第三个电离主峰应位于16.9 eV附近, 那么16.0 eV处又为何电离峰? 光电子能谱实验中HOF的合成途径为液态或固态水与氟气在Kel-F容器中反应形成, 这一过程将产生多种副反应, 然后在室温下用气流将生成的HOF转移, 这一过程也可能会夹杂着未除净的反应物, 最后可能的物种有F2、H2O、O2、O3、F2O、HF、H2O2. 这些分子的光电子能谱实验结果显示, H2O、O2、O3和H2O2在16.0 eV附近不存在电离峰, F2在15.83 eV处有一电离峰, HF和F2O分别在16.13和16.17 eV有电离峰出现. 综上, 我们认为文献光电子能谱实验中出现的16.0 eV电离峰并非来自HOF, 而可能为反应物F2或副产物HF、F2O导致的电离, HOF的第三电离峰应位于16.9 eV附近.

3.3 电离态结构、绝热电离势

分子的绝热电离势一般通过光电子能谱或光电离质谱等实验方法测定, 理论上绝热电离势计算需要优化电离态分子结构, 常用的电离势计算方法如扩展Koopmans理论、外价层格林函数法OVGF、基于格林函数的三阶代数图表构建法ADC(3)等方法都不能进行结构优化而只能计算垂直电离势, SAC-CI方法虽能优化结构, 但其优化过程采用数值梯度, EOM-CCSD则不仅可用解析梯度对电离态结构优化, 还可应用二阶导数结合有限差分法进行谐振计算和非谐分析, 这对通过分子轨道、分子结构和分子振动信息理解电离态、帮助归属光电子能谱具有重要意义. 表 3列出了利用EOM-CCSD获得的HOF电离态结构和谐振频率, 同时也用SAC-CI得到了五个电离态的平衡结构, 前两个电离态还用多种直接的CC方法进行计算. EOM-CCSD计算的第一电离态结构ROF=1.3010 Å, 与直接的CCSD计算结果1.2998 Å几乎一致, 这点也得到了SAC-CI结果的验证, 与基态的ROF=1.4171 Å相比ROF键长减小了0.116 Å, 依据光电子能谱理论, OF键的力常数将会增加, 对应OF伸缩振动频率增加, EOM-CCSD计算的第一电离态OF谐振频率为1206 cm-1, 明显大于基态994.6 cm-1, 因而该态应来自于一个反键轨道电子电离, 从头算轨道成份分析显示, 最外层轨道为O、F原子结合而成的反键π轨道, 支持了结构优化、谐振频率计算的正确性和上述分析的合理性, 该态在光电子能谱上应为一宽谱带, 其精细振动谱带需高分辨率的紫外光电子能谱实现. HOF第二价层电离态A′, 轨道成份表明其主要来自于O、F原子上的非键电子, 这些电子对成键影响不大, 因此该电离态分子结构变化不明显. 计算结果显示, 所有电离态中该态的ROF与基态结构最接近, 这也可能导致该态的垂直电离势和绝热电离势相差不大, 计算显示仅有0.26 eV, 该态在光电子能谱上应为一相对尖锐的峰. 相应的谐振频率与基态变化也不会大, 该态OF的伸缩振动频率872 cm-1是所有五个电离态中最接近基态的. 然而实际轨道还受其它键的影响导致键角发生了较大变化, 对应谱带应有轻微加宽, 遗憾的是目前还没有该峰的谱图报道. 对于第三个电离态, EOM-CCSD给出的绝热电离势为16.32 eV, SAC-CI给出的值要小于EOM-CCSD约0.2 eV, 光电子能谱实验显示仅为15.9 eV, 从优化结构来看, EOM-CCSD与SAC-CI值非常一致, 表明两种方法确认的电离态是一致的, 并不存在态不同的问题, 因此, 15.9 eV也需要被更加精确的实验检验. 两种理论的差异主要来自于包含算符不一致导致的绝对能量差异较大引起, 可望通过包含三激发的电离态优化技术或SAC-CI计算时增大活性空间以及减小算符纳入阈值等方式来提高一致性. 第四个电离态2A′, EOM-CCSD和SAC-CI优化的结构基本一致, 计算的绝热电离势值也非常接近约17.3 eV. 对于HOF的第五个价电离态结构, 结构优化时出现能量大幅震荡, 尽管我们采用不同优化算法、收敛加速、放松收敛等措施, 依然无法保证其收敛到合理的电离态结构, SAC-CI却能容易达到收敛. 可以看出, 该电离态结构与基态十分相似, 对应的绝热电离势为19.97 eV.

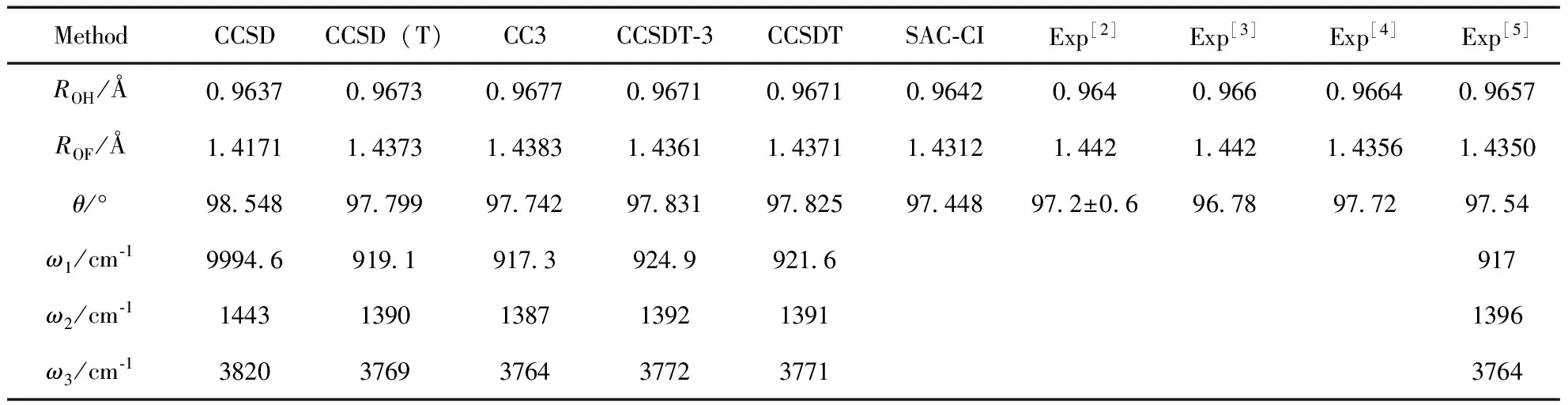
表 1 HOF基态平衡结构、谐振频率

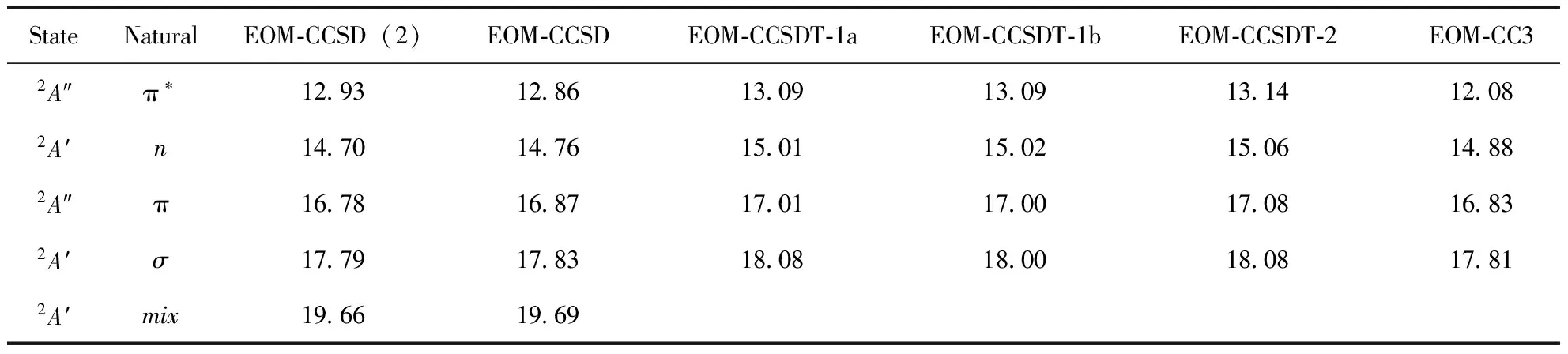
表 2 HOF价层垂直电离势

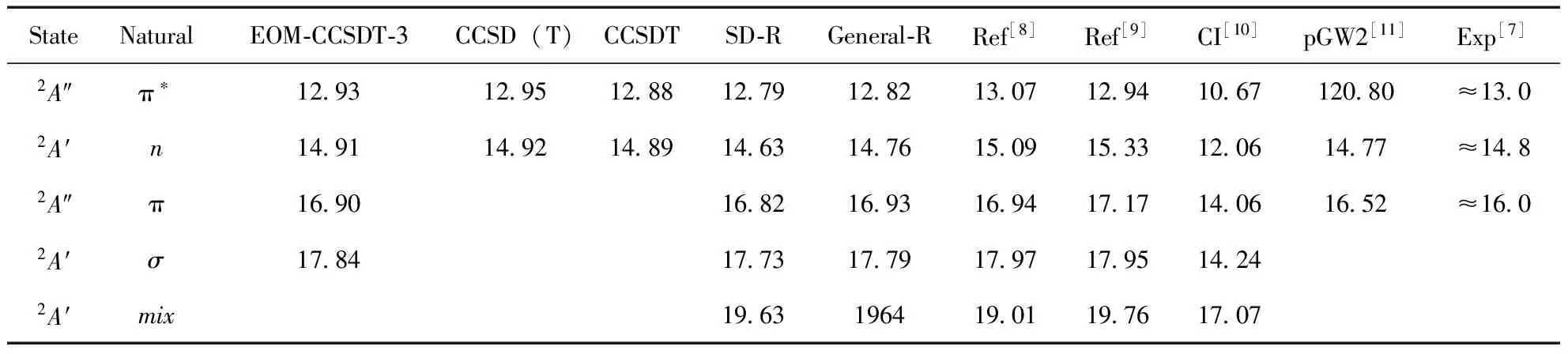
续表2

表 3 HOF电离态平衡结构、谐振频率和绝热电离势

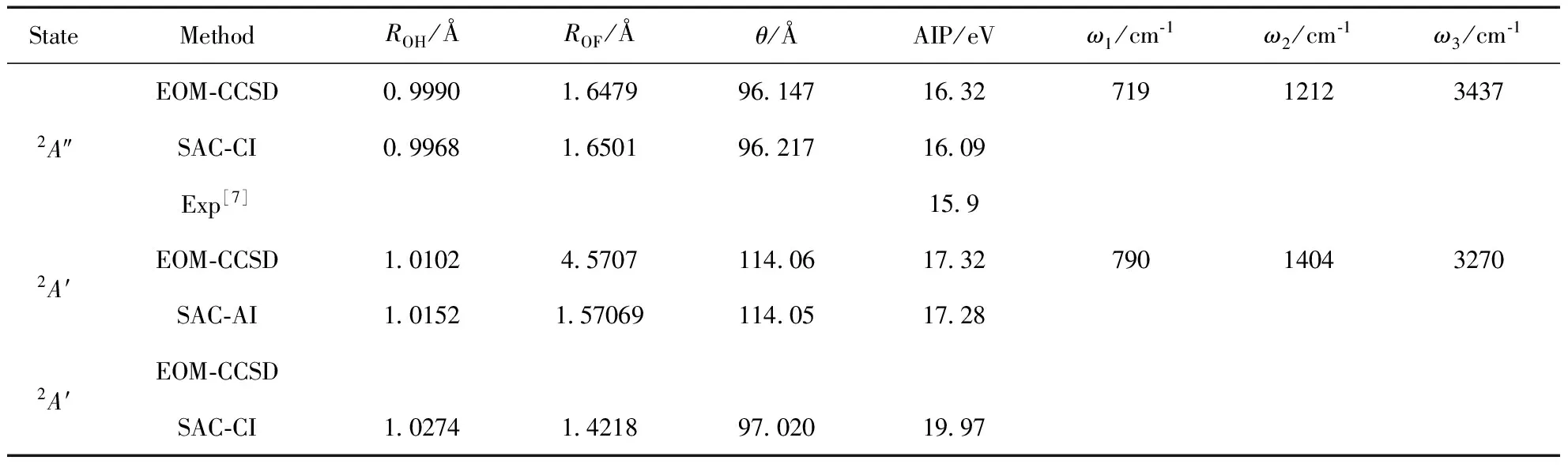
续表3

4 结 语

运用包含迭代三激发的多种运动方程耦合簇变体对HOF的价层垂直电离势进行精确计算, 澄清了早期光电子能谱对2A′态的归属错误, 预计的第三电离峰位于16.9 eV, 而非光电子能谱测得的16.0 eV, 并对16.0 eV来源进行了解释. 最后应用EOM-CCSD和SAC-CI优化得到了各电离态的结构, 从而获得其绝热电离势, 进而在优化结构上获得电离态谐振频率, 依据已知光电子能谱和键长、频率之间的关系对各态合理性进行了验证和分析, 对未知电离峰的峰型进行了估计. 目前计算成功将迭代三激发运动方程耦合簇方法应用到HOF的电离态精确计算, 能为HOF将来更加精确的光电子能谱实验提供理论依据, 同时对我们进一步研究其它分子具有指导意义.

[1] Ge M F, Ma C P. Reactive halogen chemistry[J].Progress.In.Chem., 2009, 21(2/3)： 307(in Chinese) [葛茂发, 马春平. 活性卤素化学[J]. 化学进展, 2009, 21(2/3)： 307]

[2] Kim H, Pearson E F, Appelman E H. Millimeter-wave spectrum and structure of hypofluorous acid：HOF and DOF[J].J.Chem.Phys., 1972, 56： 1.

[3] Pearson E F, Kim H. Centrifugal distortion analysis of hypofluorous acid：HOF and DOF[J].J.Chem.Phys., 1972, 57(10)： 4230.

[4] Thiel W, Scuseria G, Schaefer H F,etal. The anharmonic force fields of HOF and F2O[J].J.Chem.Phys., 1988, 89(8)： 4965.

[5] Halonen L, Ha T K. Equilibrium structure and anharmonic force field of hypofluorous acid, HOF[J].J.Chem.Phys., 1988, 89(8)： 4885.

[6] Berkowitz J L, Appelman E H, Chupka W A. Photoionzation of HOF with mass analysis[J].J.Chem.Phys., 1973, 58(5)： 1950.

[7] Berkowitz J L, Dehmer J L, Appelman E H. Photoelectron spectrum of hypofluorous acid, HOF[J].Chem.Phys.Letts., 1972, 19(3)： 334.

[8] Chong D P, Herring F G, McWilliams D. The vertical ionization potentials of hypofluorous acid as calculated by perturbation corrections to koopmans’ theorem[J].Chem.Phys.Lett., 1974, 25(4)： 568.

[9] Alti G De, Decleva P, Lisini A. On the validity of the Xamethod in the computation of ionization potentials, a comparison of the results for small molecules[J].Chem.Phys., 1982, 66： 425.

[10] Decleva P, Lisini A. 2h-1p CI calculations of ionization potentials of small molecules：corrections to the Koopmans theorem[J].Chem.Phys., 1985, 97： 95.

[11] Hu C H, Chong D P, Casida M E. The parametrized second-order Green function times screened interaction (pGW2) approximation for calculation of outer valence ionization potentials[J].J.Elect.Spectro.Rel.Pheno., 1997, 85： 39.

[12] Tang H Y, Chen H J, Cheng X L,etal. Theoretical calculation of valence shell ionization potentials ofXF3(X= N, P, As) using the equation-of-motion coupled cluster method[J].Acta.Phys.Sin., 2011, 60： 053301 (in Chinese)[唐海燕, 陈恒杰, 程新路, 等.XF3(X=N,P,As)价层电离势的运动方程耦合团簇理论计算[J]. 物理学报, 2011, 60：053301]

[13] Stanton J F, Gauss J. Revision 0.1 June 2010 CFOUR is a program package for performing high-level quantum chemical calculations on atoms and molecules.

[14] Frisch M J, Trucks G W, Schlegel H B. Gaussian 03, Revision D1. Pittsburgh PA： Gaussian Inc, 2005.

The study of ionized states of HOF using the equation of motion coupled cluster approach

CHEN Heng-Jie1, GUO Lei2, FANG Wang1, LIU Feng-Kui1

(1.School of Mathematics and Physics, Chongqing University of Science and Technology, Chongqing 401331, China;2. School of Chemistry and Chemical Engineering, Chongqing University, Chongqing 400044, China)

The outer valance shell ionization potentials of HOF have been calculated using the equation of motion coupled cluster approach with single and double excitations(EOM-CCSD), several variants included iterative triplet excitations (EOM-CCSDT-i,i=1a,1b,2,3 and EOM-CC3) have also been applied. The structures of ionized states have been optimized using EOM-CCSD and adiabatic ionization potentials have been evaluated, furthermore, harmonic frequencies have been obtained. At the same time, symmetry adapted cluster configuration interaction (SAC/SAC-CI) has also been performed in this work. It shows that results from EOM-CC3 and EOM-CCSDT-3 are closed to the EOM-CCSDT, the latter included all of triplet excitations. EOM-CC results are consistent with SAC-CI, we find the assignment for the2A′ ionized state from the photoelectron spectrum(PES) is not `correct and reassignment it. The third vertical ionization potential of HOF is located about 16.9 eV and not 16.0 eV given by PES.

HOF; The equation of motion coupled cluster approach (EOM-CC); Symmetry adapted cluster configuration interaction (SAC-CI); Outer shell ionization potential

103969/j.issn.1000-0364.2015.02.008

2013-09-13

重庆市教委科学技术研究项目(KJ121419);重庆科技学院研究基金(CK2010B05)

陈恒杰(1980—),男，汉族,甘肃人,硕士,主要研究分子光谱.E-mail： nwwolfchj@gmail.com

O561.3

A

1000-0364(2015)02-0219-06