金属Li相稳定性的第一性原理研究

林欣悦， 张 会

(沈阳大学师范学院， 沈阳 110044)

金属Li相稳定性的第一性原理研究

林欣悦， 张 会

(沈阳大学师范学院， 沈阳 110044)

Li在常温常压下为体心立方结构(bcc)， 随着压力和温度的变化会发生结构转变.本文应用第一性原理方法研究了Li的9R，fcc，hcp和bcc四种不同结构相在基态和有限温度下的相对稳定性.计算表明Li在低温时的最稳定相为六角堆垛的9R相，而且随着温度的变化会发生结构相变，最终在高温时(370K)转变为bcc相.

第一性原理; 锂; 结构相变

1 引 言

金属锂(Li)在地壳中的储量丰富，是最轻的金属，因此在储能工业如锂电池中受到了广泛地关注.在室温时，Li在常压下为体心立方(bcc)结构.研究证明，随着压力的增大Li会发生结构相变[1].除了压力，温度也可以影响Li的结构，Li可能存在其它几种低温结构，例如面心立方结构(fcc)、体心立方结构(bcc)、以及六角密堆结构(hcp)等.目前，这些结构的相对稳定性随着温度的变化的关系仍然存在争议.早在1947年，Barrett[2]指出Li在低于70K时为hcp相.在1980年，多晶中子散射实验[3]指出Li在低温时既不是fcc也不是hcp.在1984年，Overhauser[4，5]提出Li的低温相结构以9层密堆面的顺序堆垛，称为9R结构.在1986年，Berliner等[6]用中子散射的方法发现Li在20K时为9R结构.Bajpai等[7]基于修正的Hatree-Fock 方程和自洽赝势方法研究了Li的晶格动力学，计算出了马氏体相变温度，hcp-bcc为147K，fcc-bcc 为74K.Bajpai的工作由于不是第一性原理方法，其可靠性受到实验参数的制约.因此Staikov等[8]用第一性原理方法研究了块体Li的热力学性能，基态总能计算的结果竟然是hcp>bcc>9R>fcc，但fcc和bcc两个相的自由能在200K时还未相交.

本文应用密度泛函理论方法(DFT)[9，10]研究了Li的四个相(9R， hcp， fcc， bcc)的基态结构，并通过密度泛函微扰理论方法(DFPT)[11]进行了晶格动力学计算，由简谐近似研究了Li在不同温度下的结构稳定性.

2 计算方法

计算时采用PWSCF软件和超软赝势方法，平面波展开截断能为80Ry，交换关联能采用GGA-PW91近似[12]， K点网格使用Monkhorst-Pack[13]方法构建，总能随计算参数的变化小于0.1m ev/atom.基态计算时的K点网格划分分别为9R(12×12×12)，fcc(18×18×18)，hcp(18×18×12)，bcc(18×18×18).在线性响应计算时，9R，fcc，hcp，bcc各相K点网格划分分别为(12×12×12)，(12×12×12)，(10×10×6)，(12×12×12)，q空间网格划分为(4×4×4)，(4×4×4)，(5×5×3)，(4×4×4).

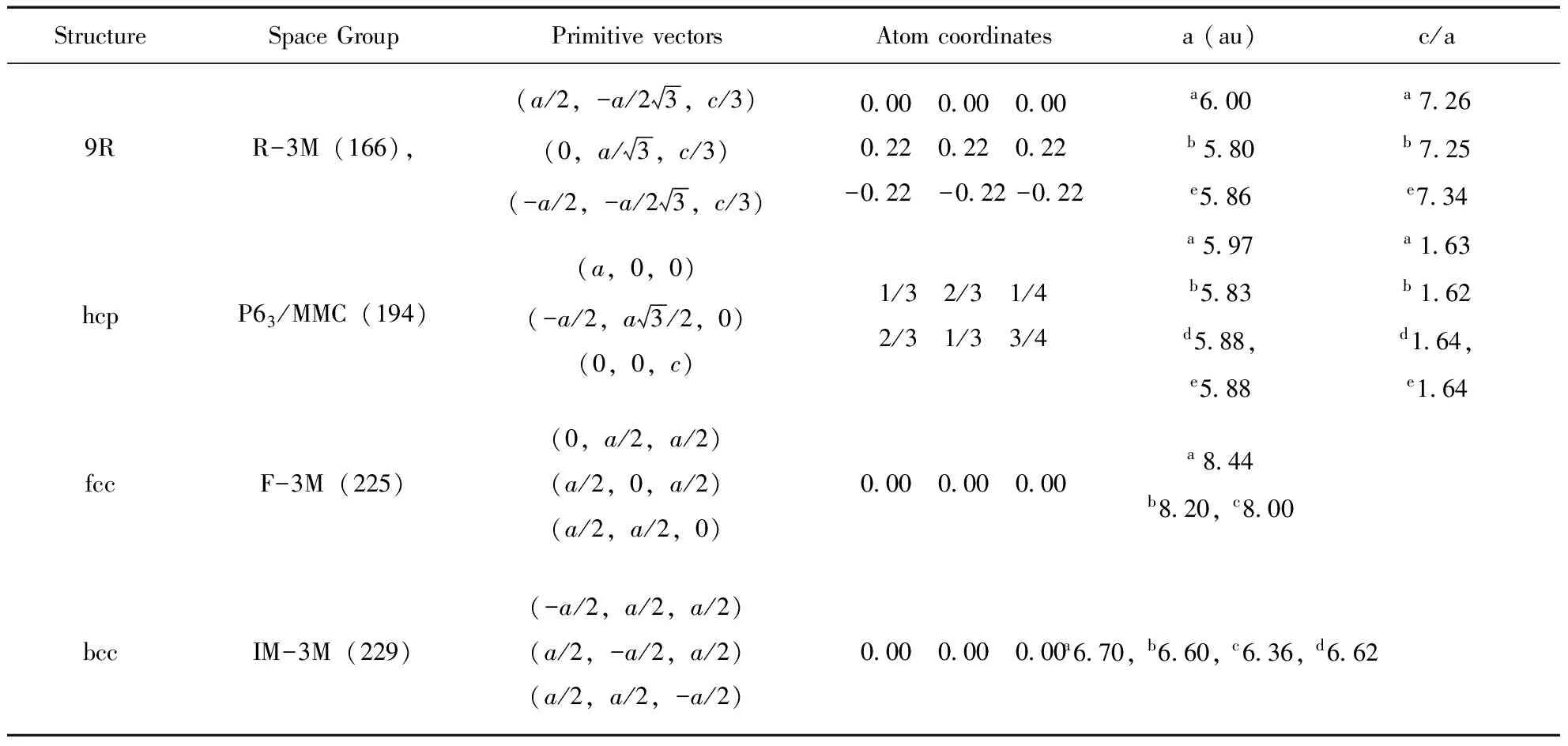
表1 Li的结构参数

aPresent calculations; Previous calculations:bStaikov[8]，cMarcel[14]; Experimental data:dBarrett[15]，eBerliner[6]

3 结果与讨论

3.1 基态计算

图 1 金属Li四种相的结构图Fig.1 The four crystal structures of Li

表1列出了四种不同结构的空间群以及计算时采用最小结构单元(元胞)，9R和 hcp的元胞中分别含有3个和2个原子，而fcc和hcp的元胞中只含有1个原子， 他们的结构如图 1 所示.本文首先对Li的四种结构进行了几何优化，结构参数在表 1 中列出.本文分别计算了不同相在十个不同体积下的基态能量，并依据普适能态方程[16]拟合出了不同体积下的总能.由表 1 可以看出，计算的晶格常数与实验值的差别在2%以内，与其它理论值也符合得比较好，因此本文的计算是可靠的.

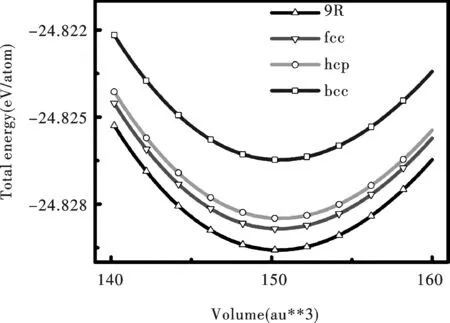
图 2 Li是不同结构总能与体积的关系Fig.2 The relation between total energy and volume of various structures of Li

图 2 给出了各相的基态总能随体积的变化.四种结构相的能量关系为Ebcc>Ehcp>Efcc>E9R.计算结果表明，基态时，纯金属Li的最稳定结构为9R相，很好地解释了实验结果.我们的结果与Bajpai等的结果[17]类似，只是fcc和hcp两个相的顺序不同，这是因为二者的能量差很小(<1meV/atom)，不能从基态计算的结果准确的判断fcc和hcp哪个相更稳定.

3.2 声子谱

本文对Li的不同结构进行了晶格动力学计算，得到了它们的声子谱. 图 3 给出了不同结构的金属Li沿对称性方向的声子色散关系，计算时采用结构优化的平衡晶格常数.由图 3 可以看出，Li的四种结构相的声子谱都不存在虚频，说明它们都是可以稳定存在的，至于Li在某一温度下以哪种结构存在，则由它们的相对自由能决定.

自由能计算的准确性依赖于对声子谱的准确计算.目前实验上只有bcc结构声子谱的实验数据，因此，图 3 给出了bcc结构声子谱计算值与理论值的对比，计算的结果与实验值在整体上符合得非常好，只是在个别点(H、N)上有较大差别;其它的理论工作[8，18]与我们的计算结果类似.因此本文中声子谱的计算是可靠的.另外，本文考虑了计算参数(K点网格、截断能)对结果的影响，不同的计算参数导致的自由能差值在1meV/atom以下.

3.3 热力学相变

由晶格动力学得到的声子谱可以计算相关的热力学性质，如熵，自由能等. 振动自由能和振动熵由下面的两个公式计算得到:

(1)

g(ω)dω

(2)

其中，n，kB， 以及g(ω)分别表示体系中包含的原子数，波尔兹曼常数以及声子态密度，g(ω)由晶格动力学得到. 总的自由能为基态总能与振动自由能之和:

(3)

其中，E为基态总能.

图4给出了以9R为参考值的其他相(hcp，fcc，bcc)的熵、热容量和自由能.从图 4 可以看出，hcp和fcc相的熵比9R相的小，而bcc相的熵最大.这说明，在四个相中，bcc相的晶格振动效应最明显.图 4 中热容量的变化趋势与熵类似.纯金属Li的bcc和fcc两个相热容量在大约160K时相交，这与Staikov等人[8]的结果相一致，只不过他们得出的相交温度为90K.四种结构的热容量在温度升高时趋于相等，因为他们都趋于经典值3R(R为气体常数).

图 3 Li的声子谱.圆圈代表bcc结构的实验值Fig.3 The phonon dispersion of Li. The cycles represent the experimental values of bcc

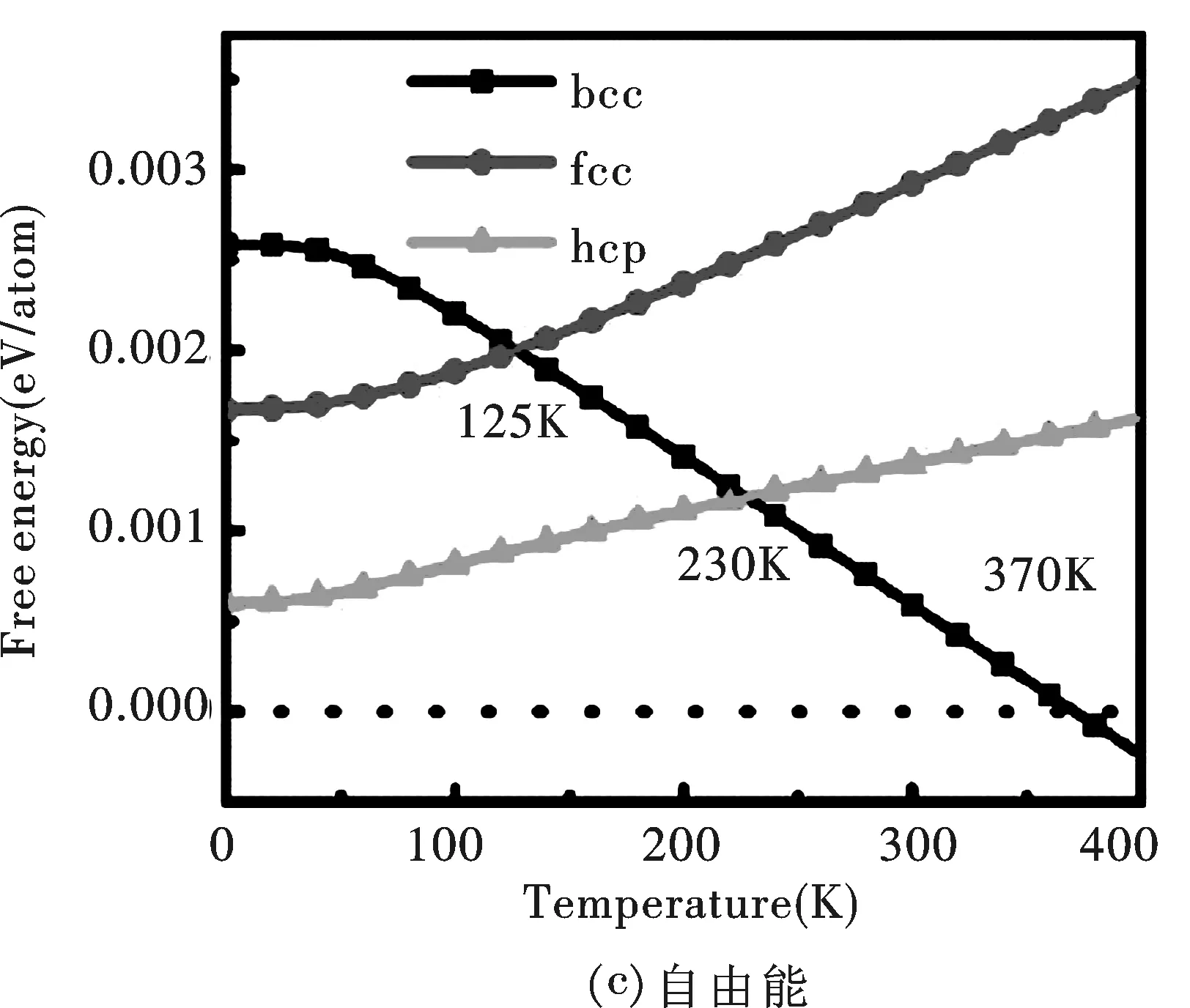
图 4 Li的bcc，hcp，fcc相与9R相的热力学函数之差:(a)熵， (b)热容量， (c)自由能Fig.4 The differences for (a)entropy， (b)capacity， (c)free energy of bcc，hcp and fcc phases relative to 9R one of Li

最后，本文研究了纯金属Li不同结构相的自由能随温度的变化关系.从图 4 中可以看出，fcc和hcp相的自由能下降得比9R相慢，因此相对自由能随温度升高是增大的;而bcc相的自由能下降最快，导致在高温时bcc相最稳定.计算表明，在温度高于370K时，bcc相成为最稳定相.纯金属Li在室温时为bcc相，但本文计算的相变温度(370K)略高于室温，这是由于计算误差造成的，这种误差很可能是由于在计算过程中未考虑热膨胀效应造成的.马氏体相变温度fcc-bcc和hcp-bcc分别为大约230K和125K，而Bajpai等[17]的结果为147K和74K.

4 总 结

我们应用密度泛函理论和密度泛函微扰理论的平面波赝势方法计算了Li的9R，fcc，hcp和bcc四种结构在基态和有限温度下的相对稳定性.基态总能大小为Ebcc>Ehcp>Efcc>E9R，说明9R为基态时的最稳定结构.晶格振动的计算表明，纯金属Li的bcc相具有更大的振动熵，因此其自由能随温度下降的最快.纯金属Li在低温时为9R相，但随着温度的升高由于晶格振动的效应而发生结构相变，在高温时(370K)转变为bcc相.

[1] Lv J， Wang Y C， Zhu L，etal. Predicted novel high-pressure phases of lithium [J].Phys.Rev.Lett.， 2011， 106: 015503.

[2] Barrett C S. A low temperature transformation in lithium [J].Phys.Rev.， 1947， 72: 245.

[3] McCarthy C M， Thompson C W， Werner S A. Anharmonicity and the low-temperature phase in lithium metal [J].Phys.Rev. B， 1980， 22: 574.

[4] Overhauser A W. Crystal structure of lithium at 4.2 K [J].Phys.Rev.Lett.， 1984， 53: 64.

[5] Wang Y R， Overhauser A W. Lattice dynamics of lithium at low temperature [J].Phys.Rev. B， 1986， 34: 8401.

[6] Berliner R， Werner S A. Effect of stacking faults on diffraction: The structure of lithium metal [J].Phys.Rev. B， 1986， 34: 3586.

[7] Bajpai R P. Self-consistent theory of the martensitic phase transformation in metallic lithium [J].Phys.Rev. B， 1975， 12: 2194.

[8] Staikov P， Kara A， Rahman T S. First-principles studies of the the thermodynamc properties of bulk Li [J].J.Phys:Condens.Matter.， 1997， 9: 2135.

[9] Kohn W， Sham L J. Self-consistent equations including exchange and correlation effects [J].Phys.Rev.， 1965， 140: A1133.

[10] Hohenberg P， Kohn W. Inhomogeneous electron gas [J].Phys.Rev.， 1964， 136: B864.

[11] Baroni S， Giannozzi P， Testa A. Green’s-function approach to linear response in solids [J].Phys.Rev.Lett.， 1987， 58: 1861.

[12] Perdew J P， Chevary J A， Vosko S H，etal. Atoms， molecules， solids， and surfaces: Applications of the generalized gradient approximation for exchange and correlation [J].Phys.Rev. B， 1992， 46: 6671.

[13] Monkhorst H J， Pack J D. Special points for Brillouin-zone integrations [J].Phys.Rev. B， 1976， 13: 5188.

[14] Sluiter M H F， Watanabe Y. First-principles calculation of the pressure dependence of phase equilibria in the Al-Li system [J].Phys.Rev. B， 1996， 53: 6137.

[15] Barrett C S. X-ray study of the alkali metals at low temperatures [J].ActaCrystallographica， 1956， 9: 671.

[16] Vinet P. Universal features of the equation of state of solids [J].J.Phys:Condens.Matter.， 1989， 1: 1941.

[17] Bajpai R P. Self-consistent theory of the martensitic phase transformation in metallic lithium [J].Phys.Rev. B， 1975， 12: 2194.

[18] Frank W， Elsasser C， Fahnle M. Ab initio force-constant method for phonon dispersions in alkali metals [J].Phys.Rev.Lett.， 1995， 74: 1791.

A study on phase stability of Li from the first-principles study

LIN Xin-Yue， ZHANG Hui

(Normal College， Shenyang University， Shenyang 110044, China)

Li possess the body centered cubic (bcc) crystal structure at the normal temperature and normal pressure， and structural phase transition occurs as temperature and pressure change. In this work， the relative phase stability of Li with 9R，fcc，hcp and bcc structures is systemically investigated from the first-principles method. The calculations reveal that the most stable Li is 9R at low temperatures. It is further demonstrated that the structure phase transition occurs as the temperature changes and bcc structure is the most stable one at high temperatures (high than 370K).

First-principles; Lithium; Structural phase transition

103969/j.issn.1000-0364.2015.02.023

2013-10-25

中国科学院“十一五”信息化专项“超级计算环境建设与应用”(INFO-115-B01)

林欣悦(1975—)，女，讲师，主要从事物理专业相关的教学和科研工作.

张会.E-mail: zhanghui@alum.imr.ac.cn

TG146

A

1000-0364(2015)02-0308-05