ZrF分子基态(X2Δ)的光谱研究
2015-03-23钱忠健刘宪云
钱忠健, 刘宪云, 李 磊
(常州大学数理学院, 常州 213164)
ZrF分子基态(X2Δ)的光谱研究
钱忠健, 刘宪云, 李 磊
(常州大学数理学院, 常州 213164)
现有ZrF分子的理论值与实验值偏差较大,且有一些光谱参数暂时还没有实验结果.本文基于群论及原子分子反应静力学推导出了ZrF分子的基态电子状态(X2Δ)和合理的离解极限.采用密度泛函理论(B3LYP, B3P86)和二阶微扰理论(MP2)方法,对Zr和F原子分别选择不同的基组进行结构优化和频率计算,根据计算结果及现有实验数据,分析得出在MP2方法下,对Zr使用LanL2DZ基组,对F使用AUG-cc-PVTZ基组计算得出的结构与实验值较为符合.然后根据优化后的方法及基组扫描了基态ZrF分子的单点能,得到的基态ZrF分子的势能曲线数值,通过Level 8.0软件拟合了势能曲线并得出了一些光谱常数.最后,由拟合得到的光谱常数(De,ωe,ωeχe,Te,Be)与实验值和其他理论值进行了比较.本文的计算结果(Re=0.1859nm,De=7.1046eV,ωe=701.25cm-1,ωeχe=2.6398cm-1,Te=-9.3473cm-1,Be=0.3104cm-1)更接近于实验值.
ZrF; 光谱常数; 势能曲线; Level 8.0
1 引 言
通过对过渡金属双原子分子的光谱研究,可以得到一些重要的分子几何结构和电子结构,他们在物理和化学的许多分支有很大的应用价值,如:化学,天文学,高温化学,催化化学以及表面科学等[1-3].在过渡金属光谱研究的初期,人们就已经研究了过渡金属卤化物的光谱,在过去的几十年中,对过渡金属的氟化物和氯化物在低电子状态方面有了重大的进展,并且对溴化物和碘化物也有了一些研究报道,对Zr的单卤化物也有一些实验报道[4-10].
理论方面,1993年,Per D. L. Siegbahn[11]运用多种混合计算方法对第二层过渡金属氟化物进行了理论研究,得到了ZrF分子的键长和离解能,并给出了其分子基态电子状态为2Δ结构.2007年,L. Cheng等[12]运用密度泛函B3lyp, SDD/6-311++G(df)基组对第二层过渡金属单卤化物进行了一系列的理论计算,其中得到了ZrF的键长,振动频率,离解能等光谱常数(Re,ωe,De,μe),并表明其基态电子结构为6σ2δ1,即2Δ结构.2009年,Khakat等[13]用B3lyp/lanl2dz方法计算了ZrF分子的键长和离解能,并表明其基态为四重态.2011年,Soorkia等[5]用多参考相互组态(IC-MRCI)方法研究了ZrF分子的基态(X2Δ)和两个低激发态(a4Σ-,b4Φ),得到了一系列的光谱常数(Re,Te,To,Be,ωe,μe).

综合以上的实验和理论结果,对ZrF分子基态的研究仅有文献[6]给出了实验数据的平衡间距,频率等光谱数据,其他的报道给出的关于键长的光谱数据均为理论计算值,且与实验值有较大的偏差.同时在所有能找到的有关ZrF分子光谱的文献中,都只给出了部分光谱参数.鉴于以上原因,我们选择ZrF分子作为研究对象,对其势能曲线及光谱常数进行深入的理论研究.
本文首先基于原子反应静力学原理[14]、群论规则和分子离解极限原理[15],分析得出了ZrF分子基态的的离解极限.然后使用Gaussian03程序包中不同的密度泛函理论和二阶微扰理论方法计算了不同的基组组合对ZrF分子基态的平衡核结构,能量和振动频率的影响,根据优化后的结果进行了单点能扫描.根据计算得到的势能曲线通过Level 8.0程序包[16]拟合得到了ZrF分子基态的光谱常数,并与报道过的实验理论值进行比较,相对于其他理论值,本文得到的结果与实验值较为接近.
2 理论方法与计算
2.1 ZrF分子的离解极限
分子势能函数都与一定的电子状态相对应,必须先确定分子的电子状态和离解极限,才能准确的表达分子的势能函数.根据原子分子反应静力学中的分离原子近似法(原子团法),用广义Wingner-Witmer规则来确定分子的离解极限和可能的电子态.Zr的基电子状态分别为3Fg,属于SO(3)群.F的基电子状态为2Pu,属于SU(n)群 .生成的线型分子ZrF,属于C∞v群.原子群可以分解为C∞v群的不可约表示的直和,通过直接和约化可得到C∞v的不可约表示和ZrF的可能电子状态.
Zr(3Fg)、F(2Pu)分解为C∞v的直和为:
3Fg→3∑-+3∏ +3Δ+3Φ
2Pu=2∑++2∏
直积并约化为:
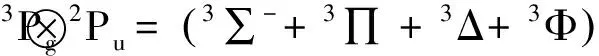
=2,4∑+⊕2,4∑-(2)⊕2,4∏(3)⊕2,4Δ (3)
⊕2,4Φ (2)⊕2,4Γ
可以看出上面结果中含有ZrF分子的2Δ态,因此从Zr(3Fg)和F(2Pu)基态原子的组合中可以得到ZrF分子的基态.根据微观过程可逆性原理和能量最低原理,我们可以确定两分子的离解极限分别为:
ZrF(2Δ)→Zr(3Pg) + F(2Pu)
2.2 结构及频率分析
本文采用密度泛函B3LYP,B3P86及二阶微扰MP2方法,对锆(Zr)原子采用LanL2DZ和LanL2MB基组,氟(F)原子则采用STO-3G, D95*, 6-311G, 6-311+G*, 6-311++G(df), 6-311++G(2df), 6-311++G(3df), cc-PVTZ, AUG-cc-PVTZ基组组合后对ZrF分子基态优化其分子结构,得到优化结构后再采用相同的方法计算振动频率.优化得到的基态平衡核间距Re,分子体系能量E以及频率计算结果ωe如表1所列.

表1 ZrF分子的结构优化和频率计算结果

表2 基态ZrF分子光谱参数
ZrF分子基态的平衡核间距Re和谐振频率ωe的实验值分别为0.1854nm和691.45cm-1.从表1的计算结果中可以看出,MP2方法结合LanL2DZ/AUG-cc-PVTZ基组计算得到的Re和ωe更接近于实验值,分别为0.1859nm和702.38cm-1,这比文献[5]和文献[12]的理论计算结果要好很多.因此,下面对ZrF分子基态(X2Δ)的单点能扫描基于MP2方法结合LanL2DZ/AUG-cc-PVTZ基组进行.
2.3 势能曲线及光谱常数
在Gaussian 03程序中用MP2方法结合LanL2DZ/AUG-cc-PVTZ基组对ZrF分子基态在0.125-0.775nm范围内等步长扫描了131个单点能.单点能扫描过程中除两原子核间距不断改变外其他条件均严格保持一致,得到势能曲线后通过Level8.0软件拟合其势能曲线得到ZrF分子基态的光谱常数:平衡键长(Re)、离解能(De)、谐振频率(ωe)、非谐振频率(ωeχe)、绝热能(Te)、平衡转动常数(Be).拟合后的势能曲线及扫描得到的势能曲线如图1所示,其中圆圈表示计算值,直线表示拟合值,从图中可以看出两条曲线基本一致.这说明运用level 8.0程序包可以很好的拟合ZrF分子的势能曲线,由此计算得出的一些光谱常数具有一定的价值.

图1 ZrF分子势能曲线Fig.1 Potential curve of ZrF molecule
表2给出了本文得到的计算结果和已报道过的光谱常数.从表中可以看出,本文计算得到的平衡间距和谐振频率相对于其他文献报道过的理论值与实验值符合更好,计算结果中Re和ωe与实验值的相对误差分别为0.27%和1.42%,而文献[5]和文献[12]中的Re,ωe与实验值的相对误差分别为1.56%,4.11%和2.43%,2.23%.本文的计算结果与实验值的误差精度要比已经报道过的理论值与实验值的误差精度高很多,所以与实验值符合的更好.在此条件下本文还预期了一些未报道过的光谱参数(ωeχe=2.6398cm-1,Te=-9.3473cm-1).
本文计算的平衡间距与振动频率均与文献[6]中给出的实验值接近,其他基态ZrF(X2Δ)分子的光谱参数均没有发现实验报道,仅有文献[4]给出了四重态ZrF分子的实验值,其中离解能De为6.49±0.2eV,谐振频率ωe为620cm1,根据文献[5]中对ZrF分子激发态的一些理论结果分析,我们猜测文献[4]中的四重态结构为ZrF的第一激发态(a4Σ-),基态分子的离解能都大于激发态,所以本文计算得到ZrF的离解能7.1046eV在数值上存在合理性,结合一些无任何实验值的光谱常数可以为进一步研究提供理论参考.
3 结 论
本文运用B3LYP,B3P86,MP2方法,对Zr选用LanL2DZ,LanL2MB基组,F选用STO-3G, D95*, 6-311G, 6-311+G*, 6-311++G(df), 6-311++G(2df), 6-311++G(3df), cc-PVTZ, AUG-cc-PVTZ基组对ZrF分子基态(X2Δ)进行结构优化和频率计算,根据优化结果选择MP2方法, LanL2DZ/AUG-cc-PVTZ混合基组计算了0.125-0.775nm范围内131个单点能,并根据这些数值点通过Level 8.0拟合了ZrF分子基态的势能曲线,得到了光谱常数,预测了一些暂时还没有数据,并对比现有成果作了一些理论分析.通过与现有实验值及理论值比较,可以看出本文得出的一些光谱常数比已报道的理论值更接近于实验值,这为Zr单卤化物的研究提供了很好的理论参考.
[1] Weltner W Jr. Stellar and other high-temperature molecules[J].Science, 1967, 155: 155.
[2] Rao C N R. Transition metal oxides[J].Annu.Rew.Phys.Chem., 1989, 40: 291.
[3] Wojciechowska M, Haber J, Lomnicki S,etal. Structure and catalytic activity of double oxide system: Cu-Cr-O supported on MgF2[J].J.Mol.Catal. A, 1999, 141: 155.
[4] Hildenbrand D L, Lau H K. Thermochemistry of gaseous ZrF, ZrF2, and ZrF3[J].J.Chem.Phys., 1997, 106: 6349.
[5] Soorkia S, Shafizadeh N, Gaveau A,etal. Determination of the ground electronic state in transition metal halides: ZrF[J].J.Phys.Chem. A, 2011, 115: 9620.
[6] Martinez A, Morse M D. Spectroscopy of diatomic ZrF and ZrCl: 760-555 nm[J].J.Chem.Phys., 2011, 135: 024308.
[7] Jordan K J, Lipson R H, McDonald N A,etal. The C4П-4Σ band system of ZrCl near 410 nm[J].Chem.Phys.Lett., 1992, 193: 499.
[8] Ram R S, Bernath P F. Fourier transform infrared emission spectroscopy of the C4D-X4F system of ZrCl[J].J.Mol.Spectrosc., 1997, 186: 335.[9] Ram R S, Bernath P F. Fourier transform emission spectroscopy of the [12.8]2Φ-a2Φ system of TiCl[J].J.Mol.Spectrosc., 1999, 196: 235.
[10] Ram R S, Adam A G, Sha W,etal. The electronic structure of ZrCl[J].J.Chem.Phys., 2001, 114: 3977.
[11] Siegbahn P E M. A comparative study of the bond strengths of the second row transition metal hydrides, fluorides, and chlorides[J].Theor.Chim.Acta,1993, 86: 219.
[12] Cheng L, Wang M Y, Wu Z J,etal. Electronic structures and chemical bonding in 4d transition metal monohalides[J].J.Comput.Chem., 2007, 28: 2190.
[13] Kharat B, Deshmukh S B, Chaudhari A. 4d transition metal monoxides, monocarbides, monoborides, mononitrides, and monofluorides: A quantum chemical study[J].Int.J.Quant.Chem., 2009, 109: 1103.
[14] Zhu Z H.Atomicandmolecularreactionstatics[M].Beijing: Science Press, 1996 (in Chineses)[朱正和.原子分子反应静力学[M].北京:科学出版社, 1996]
[15] Zhu Z H, Yu H G.Molecularstructureandmolecularpotentialenergyfunction[M]. Beijing: Science Press, 1997 (in Chinese)[朱正和, 俞华根. 分子结构与分子势能函数[M]. 北京: 科学出版社, 1997]
[16] Le Roy R J. Level 8.0AcomputerprogramforsolvingtheradialSchrÖdingerequationforboundandquasiboundlevels[R]. University of Waterloo Chemical Physics Research Report, 2007, No. CP-663.
Study on spectrum for the ground state (X2Δ) of ZrF molecule
QIAN Zhong-Jian, LIU Xian-Yun, LI Lei
(School of Mathematics and Physics, Changzhou University, Changzhou 213164, China)
The existing theoretical and experimental values of ZrF molecule deviate significantly, and some spectral parameters have no experimental values temporarily. In this paper, based on the group theory and the atomic and molecular reaction statics, the reasonable dissociation limits and the ground state(X2Δ) for ZrF molecule have been derived. Zr and F atoms respectively select different basis sets to make structural optimization and frequency calculation with density functional theory (B3LYP, B3P86) and second-order perturbation theory (MP2) methods. According to the computed results and the existing experimental values, we find that by using MP2 methods, the structures derived from the MP2 calculation are fairly consisted with the experimental values through the LanL2DZ basis sets for Zr atom and the AUG-cc-PVTZ basis sets for F atom. Then the potential energy curve of the ground states of ZrF molecule is scanned by the Mp2/LanL2DZ/AUG-cc-PVTZ level of theory, and level 8.0 software is used to fit the potential energy curve. At last, the spectroscopy constants (De,ωe,ωeχe,Te,Be) related to the potential energy curve are calculated and compared with the existing theoretical and experimental values. The calculated results of this paper (Re=0.1859nm,De=7.1046eV,ωe=701.25cm-1,ωeχe=2.6398cm-1,Te=-9.3473cm-1,Be=0.3104cm-1) are closer to the experimental values.
ZrF; Spectroscopy constants; Potential energy curve; Level 8.0
103969/j.issn.1000-0364.2015.02.007
2013-12-8
教育部第46批留学回国人员科研启动基金(2013z0031);常州第十八批科技计划(应用基础研究)(2012Z0125);常州大学科研启动基金(ZMF1102073)
钱忠健(1990—),男,汉族,江苏常熟人,在读硕士生,主要从事凝聚态物理方面研究.
刘宪云. E-mail: xyliu@cczu.edu.cn
O561.1
A
1000-0364(2015)02-0214-05
