基于遗传优化的RBF-BP神经网络电液伺服阀故障诊断算法研究

刘春艳， 樊立萍

(沈阳化工大学 信息工程学院， 辽宁 沈阳 110142)

基于遗传优化的RBF-BP神经网络电液伺服阀故障诊断算法研究

刘春艳， 樊立萍

(沈阳化工大学 信息工程学院， 辽宁 沈阳 110142)

电液伺服阀是液压伺服系统的核心元件，因此是故障诊断的重点对象，其故障原因经常呈现出非线性和不确定性等复杂状态.单一的BP网络是全局逼近神经网络，学习速度很慢，容易陷入局部极小，易产生震荡等不足，RBF网络是局部逼近神经网络，训练速度快，在训练时不会发生震荡，也不会陷入局部极小.基于它们各自的优缺点，通过将RBF神经网络和BP神经网络有效地结合在一起，取长补短，建立一个由RBF子网和一个BP子网两部分串联构成的双隐藏层RBF-BP组合神经网络.该网络既具有BP网络较好的泛化性能，又具备RBF网络较快的逼近速度.用遗传算法优化该神经网络的初始权值和阈值.该网络同时具有 RBF 网络和 BP 网络的优点，适用于复杂非线性系统的故障检测.

故障诊断； RBF-BP神经网络； 遗传算法

电液伺服阀在液压伺服系统中起着举足轻重的作用.它的响应速度快，控制精度高，但由于其元件比较复杂，精密度高，且常在高温高压环境下工作，因此故障出现的频率较高.而且一旦出现故障，不仅昂贵的诊断费用直接影响企业的经济效益，还可能使整个工作线停止，严重时可能引起人员伤亡，造成严重的经济损失，所以对电液伺服阀的故障进行有效诊断与维修具有重要的现实意义[1].

故障诊断技术发展至今，有智能故障专家系统、灰色系统理论、神经网络理论、模糊理论等各种诊断方法.神经网络具有很好的非线性函数逼近能力，结合电液伺服阀的特性，采用人工神经网络对其进行故障诊断是一种有效的手段.BP网络自学习、自适应能力强，但学习速度慢、易陷入局部最优，而RBF网络具有学习快、能够避免陷入局部最优等优点[2]，但对训练样本依赖性强，泛化能力较差.因此本文将两种单一网络相互结合构成一个双隐藏层RBF-BP组合神经网络对电液伺服阀进行故障诊断.

1 电液伺服阀的组成

电液伺服阀通常由力矩马达(或力马达)、液压放大器、反馈机构(或平衡机构)三部分组成.如图1所示.

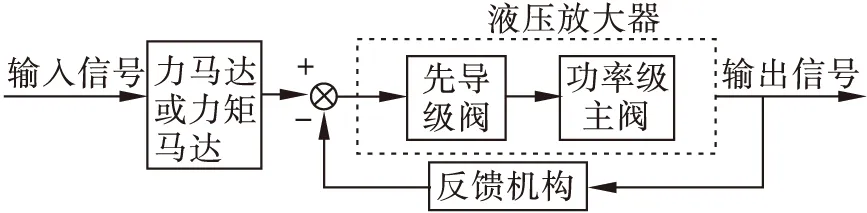
图1 电液伺服阀的组成原理

输入信号由力矩马达将电气控制信号转化为力矩或力来控制液压放大器的运动；由液压放大器控制液压能源流向液压执行机构的流量或压力；反馈机构(平衡机构)的作用是将输出流量或输出压力反馈到先导级阀的输入端或比例放大器的输入端，获得所需的伺服阀压力-流量性能，解决功率级主阀的定位问题[1].

电液伺服阀主要的失效形式有磨损(例如主阀芯控制窗口棱边磨损和主阀套密封破损)、卡紧(如阀芯卡死或卡滞)、温升等几种.

2 RBF-BP组合神经网络结构和参数设计

RBF-BP组合神经网络是由一个RBF子网和一个BP子网两部分组合而成的双隐藏层神经网络，第一隐藏层结点的传递函数使用高斯函数，第二隐藏层结点的传递函数使用Sigmoid型函数[3].

径向基神经元模型[4]如图2所示.

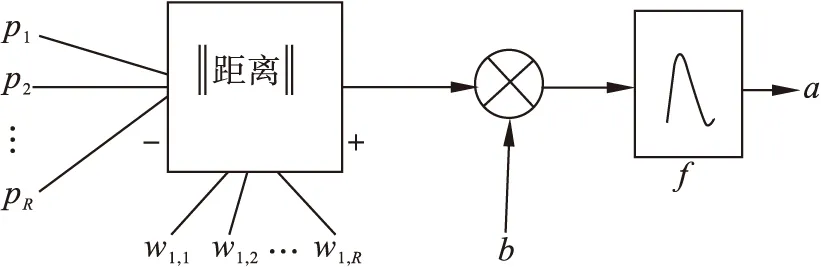
图2 径向基神经元

其径向基传输函数为radbas,其输出表达式为:

a=f(‖W-P‖·b)=

radbas(‖W-P‖·b),

(1)

(1)式也可表示为:

a(n)=radbas(n)=e-n2,

(2)

其中：

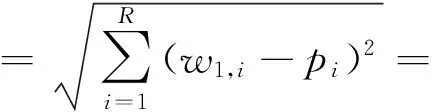
[(W-PT)(W-PT)T]1/2

(3)

BP神经元模型[5]如图3所示.

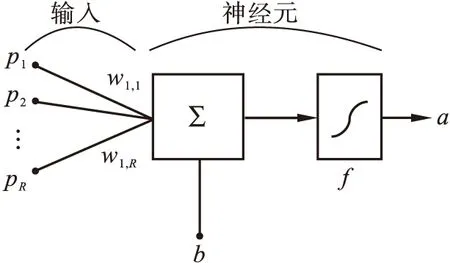
图3 BP神经元

若传递函数为tansig,其输出表达式为:

a=f(Wp+b)=tansig(Wp+b);

(4)

(4)式也可表示为:

(5)

若传递函数为logsig,其输出表达式为:

a=f(Wp+b)=logsig(Wp+b),

(6)

(6)式也可表示为:

(7)

RBF-BP组合神经网络模型结构如图4所示.其中P=(p1，p2…pi)T是输入向量，pi是输入向量的第i个元素，w1,j(i)是pi对应第一隐藏层第j个神经元的权值，(b11…b1j)T是第一隐藏层的阈值向量，w2,n(j)是第一隐藏层第j个神经元对应到第二隐藏层第n个神经元的权值，(b21…b2n)T是第二隐藏层的阈值向量，w3,k(n)是第二隐藏层第n个神经元对应到输出层第k个神经元的权值，(b31…b3k)T是输出层的阈值向量，Y=(y1，y2…yk)T是输出向量.

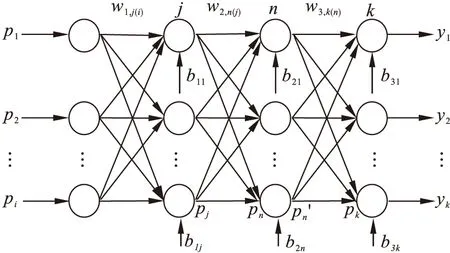
图4 RBF-BP组合神经网络

3 算法描述

采用Delta(δ)学习规则，选择均方误差(mse)作为误差准则函数，则有

(8)

式中:tk代表期望的输出;yk为网络的实际输出;m为输出层的神经元个数.

RBF-BP组合神经网络的学习过程分为两个步骤：

第一步是通过设置的网络结构，学习样本从网络的第一层向后经过隐层处理，计算各神经元的输出，传向输出层，这是正向传播.

第二步是将误差信号(理想输出与实际输出之差)按连接通路反向计算，从最后一层向前计算各权值和阈值对总差的影响(梯度)，据此不断修正网络的权值和阈值，这是反向传播.

3.1 正向传播

第一隐层第j个神经元的输出pj采用radbas函数激发，由公式(1)、(2)、(3)得:

(9)

其中l为输入层神经元个数.

第二隐层第n个神经元的输入是第一隐层所有神经元输出的加权和与阈值之和，即:

(10)

其中r为第一隐层神经元个数.根据公式(4)、(5)得第二隐层第n个神经元的输出为:

(11)

输出层第k个神经元的输入是第二隐层所有神经元输出的加权和与阈值之和，即:

(12)

其中s为第二隐层神经元个数.根据公式(6)、(7)得输出层第k个神经元的输出为:

(13)

网络第k个输出与相应理想输出tk的误差为:

ek=tk-yk,

(14)

根据公式(8)可知第p个样本的误差性能指标函数为:

(15)

3.2 反向传播

采用SCG算法调整各层间的权值和阈值.在变梯度算法中，沿变化方向进行搜索，其收敛速度比最速下降法的速度更快.学习算法如下：

所有变梯度算法的第一次迭代都是沿着最陡梯度下降方向开始进行搜索[4]：

q0=-g0

(16)

然后决定最佳距离的线性搜索沿着当前搜索方向进行：

xh+1=xh+αhqh，

(17)

qh=-gh+βhqh-1,

(18)

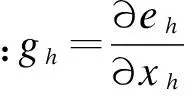
(19)

αh为搜索步长，由式mine(xh+1)决定，其结果为:

(20)

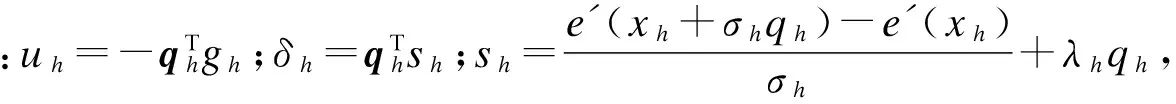
4 MATLAB实现

使用RBF-BP组合神经网络进行故障诊断，首先设计网络结构和输入输出模式，采用文献[1]中的实验数据，即在系统压力分别为3、3.5、4、4.5和5MPa，5种状态模式，16组固定电流下测得的进口压差和出口压差的实验数据.因此网络的输出采用如下形式表示：

Y=(y1，y2，y3，y4，y5);

正常状态： (1，0，0，0，0);

阀芯一端限位： (0，1，0，0，0);

一侧固定节流孔堵塞： (0，0，1，0，0);

阀芯磨损： (0，0，0，1，0);

伺服阀零位不对中： (0，0，0，0，1).

因此RBF-BF组合神经网络结构采取的是32个输入、5个输出、2个隐层数的神经网络，隐层神经元的数目与输入层神经元的个数有近似关系[11]：r=2×l+1，因此2个隐藏层的神经元个数均取65，然后创建网络并设置相应参数.调用newff函数创建双隐藏层的BP神经网络，将第一个隐藏层神经元的传递函数设置为高斯(Gauss)型函数radbas，并将第二个隐藏层和输出层神经元的传递函数设置为Sigmoid型函数tansig和logsig，采用的训练函数为trainscg并设置学习率、训练次数等相关参数.

另外，因无法准确获得网络的结构及初始连接权值和阈值，这对网络训练的影响很大.而遗传算法具有较强的鲁棒性，可以搜索全局的最优解，所以在对RBF-BP网络训练时，采用与遗传算法相结合的方式对网络的权值和阈值进行优化，获得最佳的初始权值和阈值，使优化后的神经网络能够更好地进行样本诊断.

图5是遗传优化后得到的权值和阈值矩阵X的误差进化曲线，最小误差e=0.039 42.

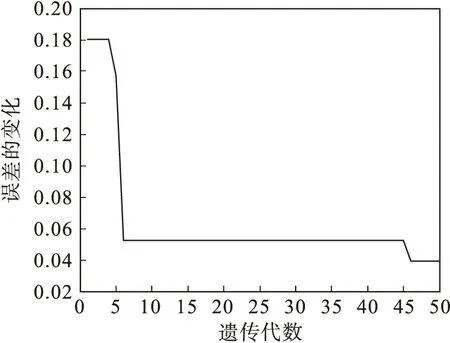
图5 误差进化曲线

图6和图7分别为使用随机权值和阈值、使用优化后的权值和阈值两种情况下的训练误差曲线.表1是输出的预测值、预测误差和训练误差.表1中测试样本预测结果Y的5行数据分别代表检测出的5种故障状态，依次为正常状态；阀芯一端限位；一侧固定节流孔堵塞；阀芯磨损；

伺服阀零位不对中.通过比较可以看出，优化初始权值和阈值后的测试样本的误差由0.391 63减少到0.039 42，训练样本的误差由0.625 51减少到0.092 99.网络的训练和样本的测试效果都得到了很大的改善.

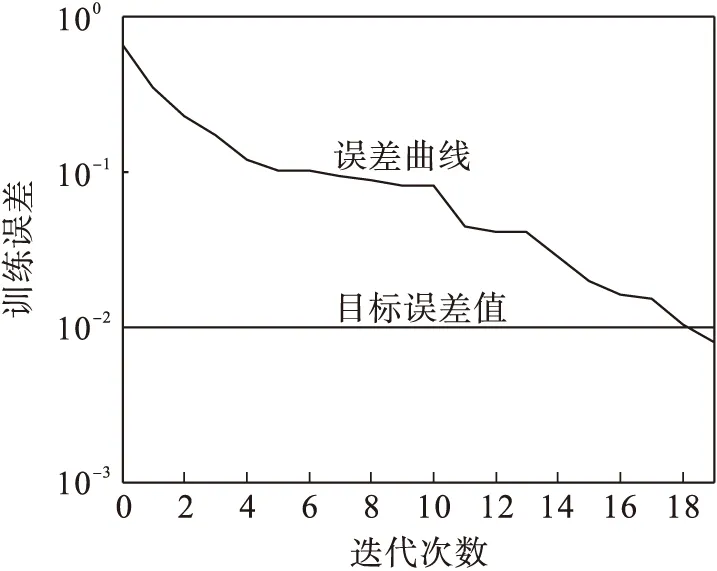
图6 随机权值和阈值训练误差曲线

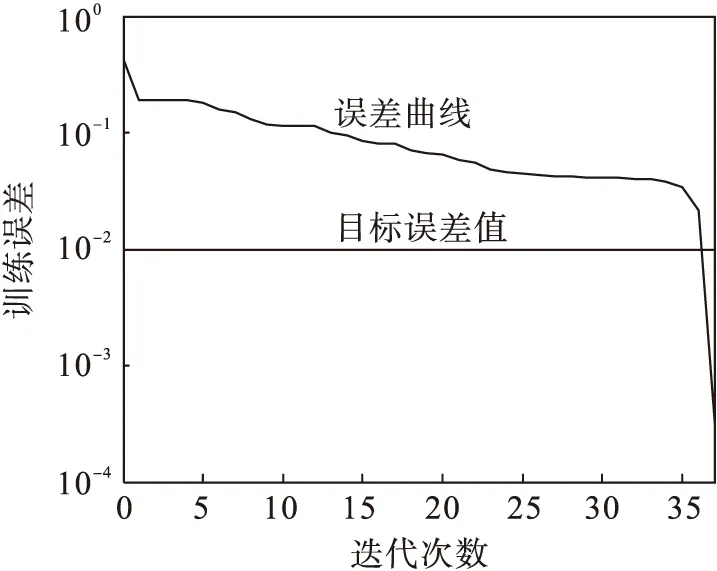
图7 优化后的权值和阈值训练误差曲线

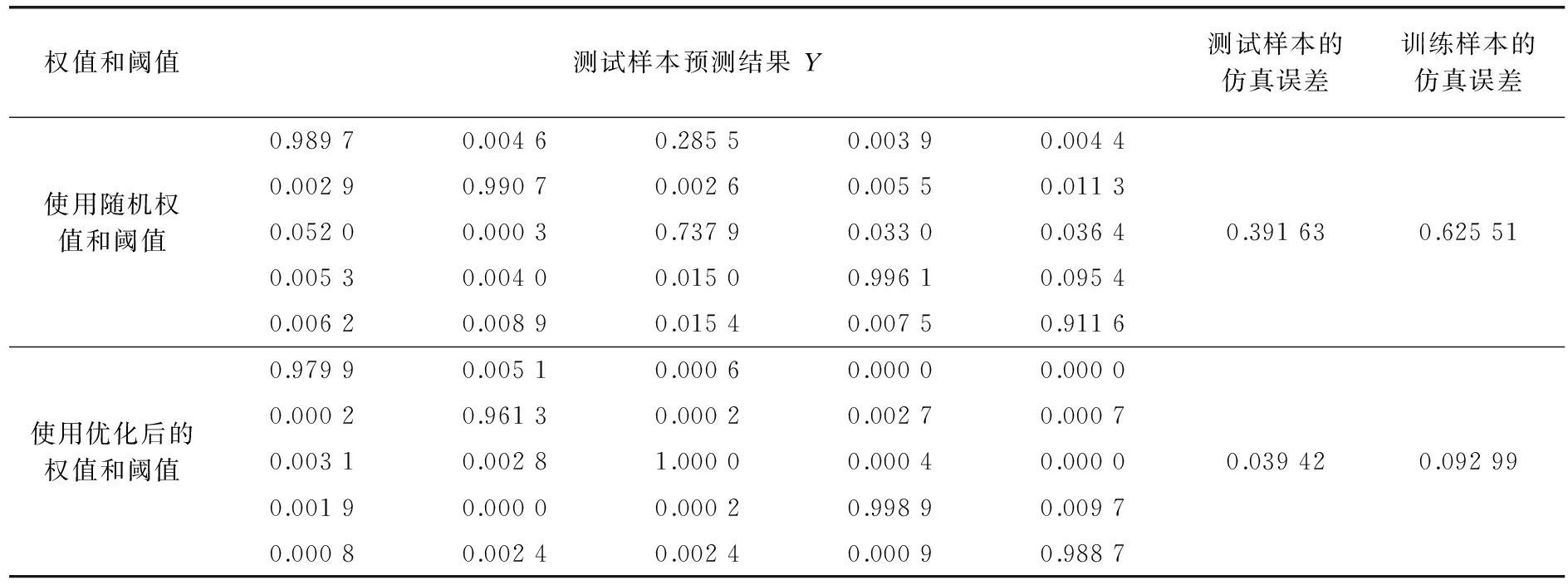
权值和阈值测试样本预测结果Y测试样本的仿真误差训练样本的仿真误差0.98970.00460.28550.00390.0044使用随机权值和阈值0.00290.99070.00260.00550.01130.05200.00030.73790.03300.03640.391630.625510.00530.00400.01500.99610.09540.00620.00890.01540.00750.91160.97990.00510.00060.00000.0000使用优化后的权值和阈值0.00020.96130.00020.00270.00070.00310.00281.00000.00040.00000.039420.092990.00190.00000.00020.99890.00970.00080.00240.00240.00090.9887

5 结 论

通过大量的样本训练，使用RBF-BP组合神经网络进行故障诊断，并采用遗传算法进行优化，得到网络的权值和阈值等参数，将测试样本输入到训练好的网络，验证了网络的正确性.且采用SCG算法能加快训练速度，网络训练次数较少，识别准确度高，能较准确的诊断出故障点，能满足系统要求.

[1] 李成.基于B-P神经网络的电液伺服阀的故障诊断[D].武汉：武汉科技大学,2010:1-45.

[2] 李仿华,王爱平,姚丽娜,等.基于遗传优化的 RBF-BP 网络的实时故障检测[J].微型机与应用,2012,31(8):90.

[3] 谌爱文.基于BP和RBF神经网络的数据预测方法研究[D].长沙:中南大学,2007:26-27.

[4] 周开利,康耀红.神经网络模型及其MATLAB仿真程序设计[M].北京:清华大学出版社,2005:101.

[5] 朱凯,王正林.精通MATLAB神经网络[M].北京:电子工业出版社,2010:193.

[6] 孙英广.神经网络在径流预测模型研究中的应用及软件实现[D].大连:大连理工大学,2005:32-34.

[7] 刘倩.城市轨道交通客流诱导系统的研究与实现[D].北京:北京交通大学,2009:34-36.

[8] 王卓宇.SCG算法优化调强放射治疗计划子野权重研究[D].广州:第一军医大学,2006:11-21.

[9] 王兆丽,王力.一个简单高效的动态手势识别方法[J].计算机工程与应用,2002(19):74.

[10]许丹,孙志林,潘德炉.钱塘江河口盐度的神经网络模拟[J].浙江大学学报：理学版,2011,38(2):235-236.

[11]史峰,王辉,郁磊,等.MATLAB智能算法30个案例分析[M].北京:北京航空航天大学出版社,2011:29-30.

Fault Diagnosis Algorithm Research of Hydraulic Servo Valve Based on Genetic Optimization of RBF-BP Neural Network

LIU Chun-yan， FAN Li-ping

(Shenyang University of Chemical Technology， Shenyang 110142， China)

The servo valve as a core component of the hydraulic servo system is the focus of fault diagnosis,and the cause of the malfunction often exhibits complex state of uncertainty and nonlinear.Single BP network is a global approximation of neural networks with some shortcomings,such as learning speed is very slow,easy to fall into local minima,and easy to produce shock.RBF network is a local approximation neural network with training speed,and it will not produce shock or trap in local minima during training.Based on their respective advantages and disadvantages,by using RBF network and BP network effectively together,this paper complements each other,and builds double combinations of hidden layers RBF-BP neural network consisting of two parts series.The network not only has better generalization performance of BP network,but also had a faster approach speed of RBF network.Genetic algorithm is used to optimize the initial weights and thresholds of the neural network.The network also has advantages of RBF network and BP network for complex nonlinear system fault detection.

fault diagnosis； RBF-BP neural network； genetic algorithm

2013-11-04

国家科技支持计划项目(2012BAF09B01)

刘春艳(1989-)，女，辽宁普兰店人，硕士研究生在读，主要从事轧机故障诊断等方面的研究.

樊立萍(1965-)，女，山东淄博人，博士，教授，主要从事复杂系统建模与控制等方面的教学与研究.

2095-2198(2015)01-0049-05

10.3969/j.issn.2095-2198.2015.01.011

TP273

A