解非线性方程的一类改进型牛顿法＊

单吉宁，蔡 静

（湖州师范学院 理学院，浙江 湖州313000）

0 引言

非线性方程求根问题源于物理学、经济学、工程计算等诸多应用学科领域．由于多数非线性方程无法求得精确解，故寻求方程的近似解显得尤为重要．牛顿迭代法（Newton method）［1］是一种非线性方程求根的经典方法，它在非线性方程的单根附近平方收敛，且此法还可用于求非线性方程的重根、复根．

近年来，具有更高收敛阶的改进型牛顿法的构建倍受关注，出现了多种改进算法，主要有算术平均牛顿法［2］（AN）、调和平均牛顿法［3］（HN）、中点牛顿法［3］（MN）、几何平均牛顿法［4］（GN）、α－幂平均牛顿法［5］（PN）．这五种算法的收敛阶都达到了3阶．文献［6］结合经典牛顿法与中点牛顿法（MN），提出了一类求解非线性方程的5阶收敛迭代算法．

上述文献中提出的各种改进型牛顿法，常用的构造思想是：利用各类均值替代经典牛顿法中的一阶导，由此获得更高的收敛阶．而所选的均值类型、修正的次数和方法会直接影响算法收敛的效果．本文结合经典牛顿法与算术平均牛顿法（AN），利用线性插值，提出一种新的改进型牛顿法，并证明其收敛阶可达6阶．同时，通过数值试验将所建立的改进型牛顿法与已有的几类牛顿改进格式进行比较，以验证所建算法的优越性．

1 新的改进型牛顿法的构建

在文献［2］中，Weerakoon和Fernando给出了收敛阶为3阶的算术平均牛顿法（AN）．具体迭代格式如下：

在上述算术平均牛顿迭代格式的基础上结合经典牛顿法，可得：

为了得到f′（zn）的显式表达式，在）和两点上用线性插值公式：得到f′（zn）的近似值为：

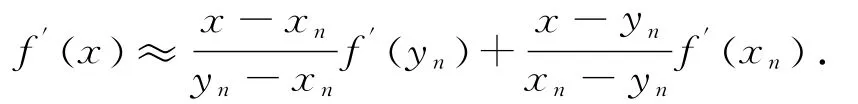
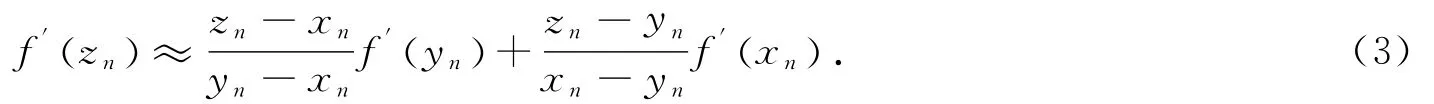
代入（3）式得：

将（4）式代入（2）式，得如下新的算法（简记为 MAN）：

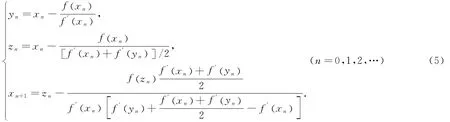
2 新算法的收敛性分析

定义［1］设数列 ｛xn｝收敛于x＊，令误差en＝xn－x＊，如果存在某个实数p≥1及正常数C，使则称数列 ｛xn｝为p阶收敛，也称相应的迭代法是p阶方法，C称为渐近误差常数．当p＝1且0＜C＜1时，称数列｛xn｝为线性收敛．当p＞1时，称数列｛xn｝为超线性收敛．

定理 设f：R→R为连续可微函数，α为fx（）在R内的单根，即有fα（）＝0，且初始值x0充分接近α，记．若0，则MAN法是6阶收敛的，且其误差方程为：

证明 设α为fx（）在R内的单根，en＝xn－α是其第n次迭代产生的误差，将fx（）在α处泰勒展开，则有：记．则有：

对上式求导可得：

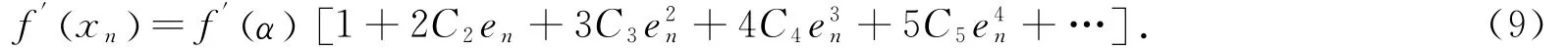
于是

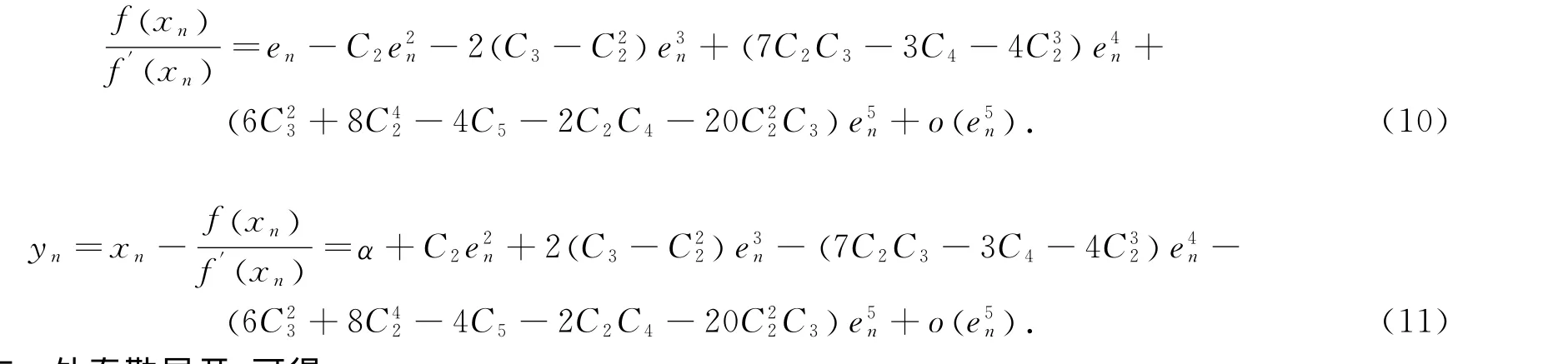
因此

将f′（yn）在α处泰勒展开，可得：

所以

因此

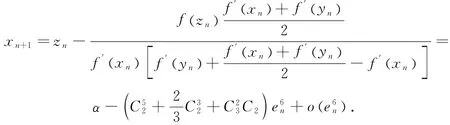
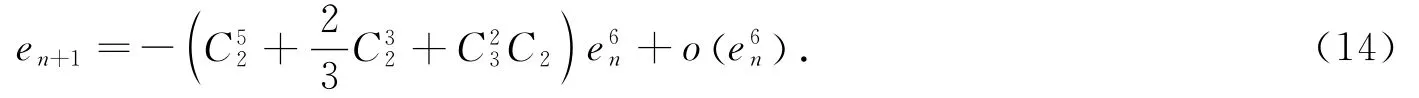
3 数值实验

选取三个非线性方程作为测试方程，将所提出的6阶牛顿改进型算法（MAN）与经典牛顿法以及几类改进型牛顿法，如AN、GN、PN等作比较，程序运行环境为matlab7．0．结果如表1～表3所示．表中x0为初值；k为迭代次数；xk为第k次迭代值；fk为每次迭代后的函数值．迭代次数的最大值为100次．

表1 f1x（）＝x3＋4x2－10＝0，精确根α＝1．36523001341410，x0＝1Table 1 f1x（）＝x3＋4x2－10＝0，accurate rootα＝1．36523001341410，x0＝1

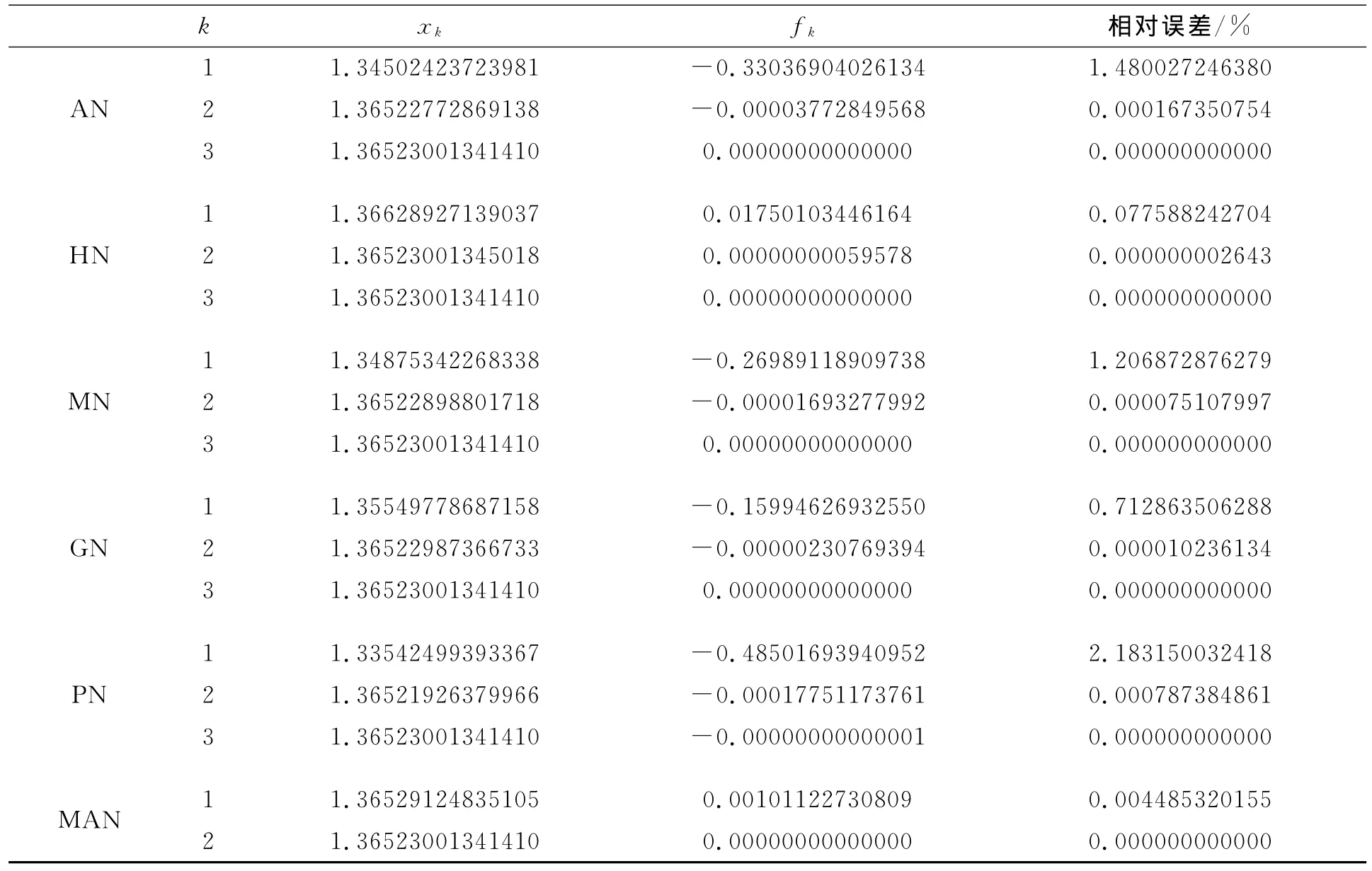
表1（续）

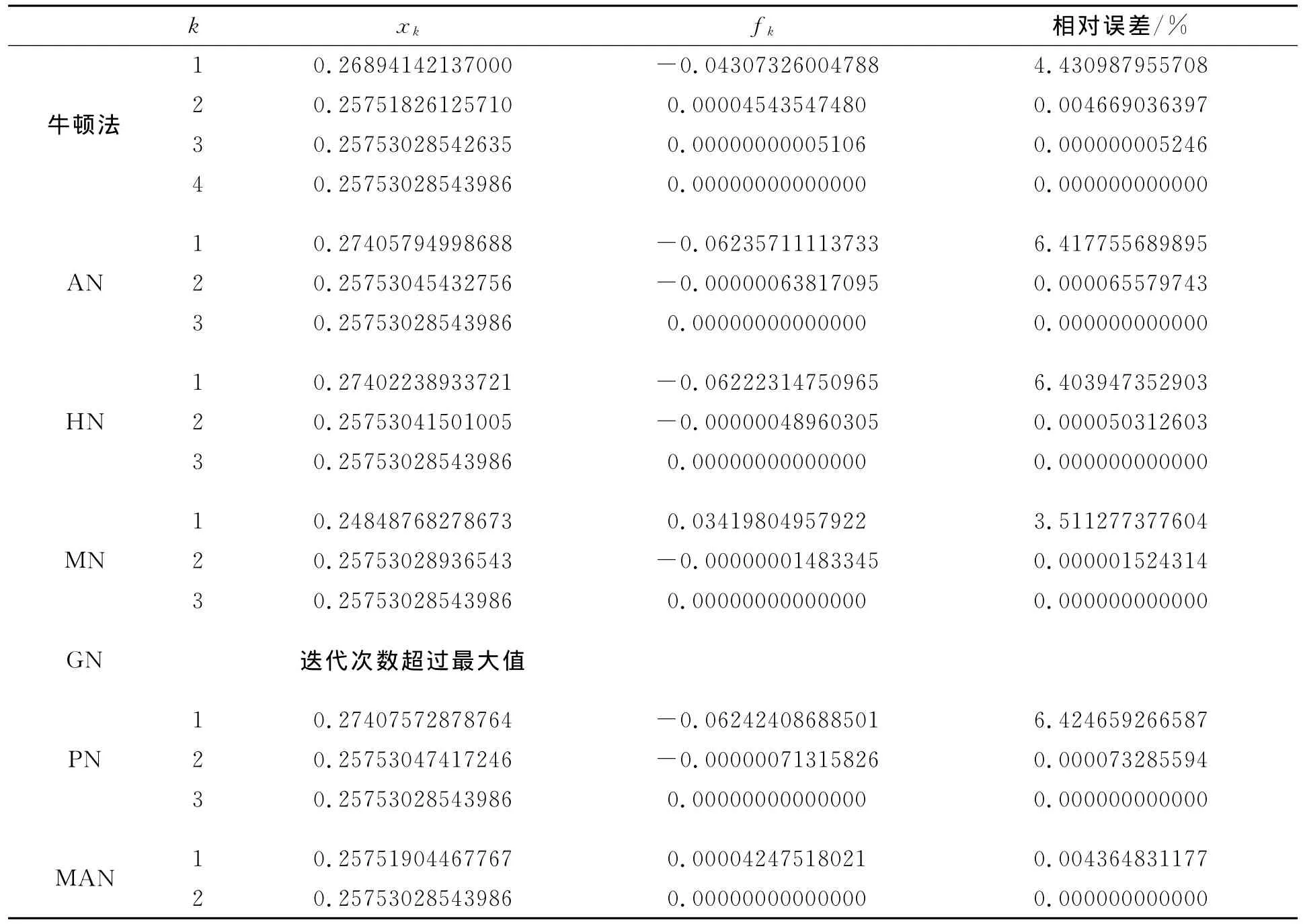
表2 f2x（）＝x2－e x－3x＋2＝0，精确根α＝0．25753028543986，x0＝1Table 2 f2x（）＝x2－e x－3x＋2＝0，accurate rootα＝0．25753028543986，x0＝1

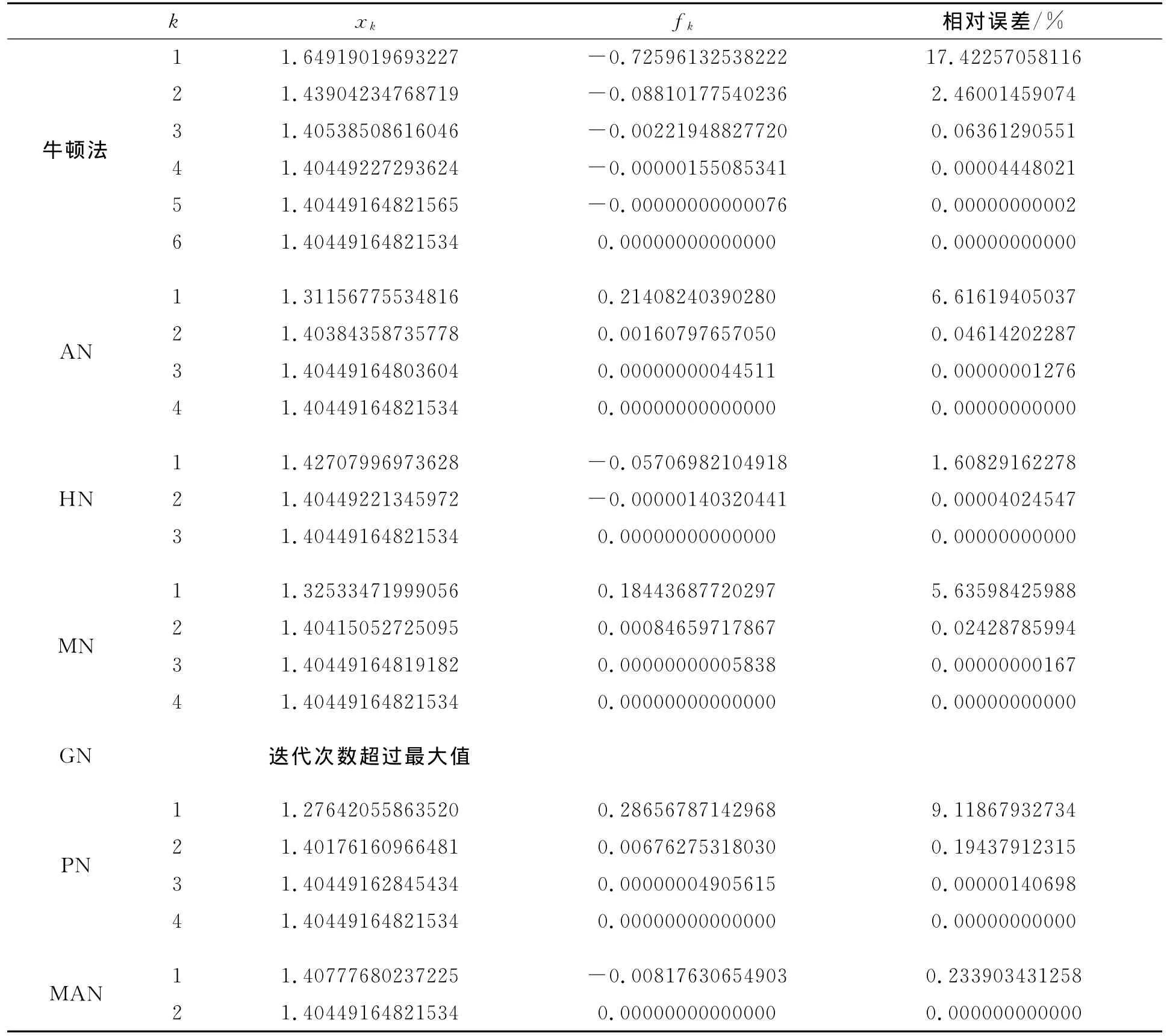
表3 f3x（）＝sin2 x－x2＋1＝0，精确根α＝1．40449164821534，x0＝1Table 3 f3x（）＝sin2 x－x2＋1＝0，accurate rootα＝1．40449164821534，x0＝1

实验表明，与经典牛顿法及上述五种改进型牛顿法相比较，本文提出的算法具有更快的收敛速度和更高的精度．

［1］白晓燕．求解非线性方程的迭代算法研究［D］．杭州：杭州电子科技大学，2009．

［2］Weerakoon S，Fernando T G I．A variant of Newton’s method with accelerated third－order convergence［J］．Appl Math Lett，2000，13（8）：87－93．

［3］Özban A Y．Some new variants of Newton’s method［J］．Appl Math Lett，2004，17（6）：677－682．

［4］Lukic T，Ralevic N M．Geometric mean Newton＇s method for simple and multiple roots［J］．Appl Math Lett，2008，21（1）：30－36．

［5］Ababneh O Y．New Newton’s method with third－order convergence for solving nonlinear equations［J］．Inter J Math Comput Sciences，2012（6）：119－121．

［6］周任沣，蔡静．一类五阶牛顿变形方法及其加速［J］．杭州师范大学学报，2011，10（6）：529－534．