基于枢纽集散和干线对流平衡的二级轴辐式零担物流网络设计

高超锋， 林庆福， 胡志华，2

(1.上海海事大学 物流研究中心， 上海 201306； 2.同济大学 经济与管理学院， 上海 200092)



基于枢纽集散和干线对流平衡的二级轴辐式零担物流网络设计

高超锋1*， 林庆福1， 胡志华1，2

(1.上海海事大学 物流研究中心， 上海 201306； 2.同济大学 经济与管理学院， 上海 200092)

针对零担物流网络设计中容易出现网络资源非均衡利用问题，分析了零担物流轴辐式网络中枢纽集散和干线对流平衡的重要性，建立基于枢纽集散和干线对流平衡的二级轴辐式物流网络混合整数规划模型.通过算例表明，考虑枢纽集散和干线对流平衡时，随着平衡程度的不断提高，枢纽集散和干线对流平衡综合度均可达到将近90%，表明综合考虑枢纽集散和干线对流的零担物流网络能够实现网络资源的均衡利用.

零担物流网络； 枢纽集散； 干线对流； 平衡； 混合整数规划

近年来，由于经济技术水平的提高，产品生命周期日渐缩短，顾客需求日益多样化、个性化，零担物流得到极大的发展，同时也对物流提出了更高的要求.零担物流网络中节点众多，并且相对分散，如果在各节点之间直达运输，则需要更多的运输车辆，耗费更高的人力成本，因此，有必要在各节点之间选择一些枢纽点，形成以枢纽点为核心的轴辐式物流网络.在地域广阔的中国，通过数个大型枢纽点形成覆盖全国的网络结构，是零担物流业发展的一大趋势.

在轴辐式物流网络中，枢纽点作为货物的集散点或中转点，是整个网络的轴心.而枢纽点间货物的流动占据比例大，且易产生规模效益.干线运输流量不平衡导致不合理运输，从而造成车辆运输资源的浪费.而枢纽集散量的不平衡使得各个枢纽点的容量得不到充分利用，导致枢纽点资源的浪费或者没有足够的物资存储空间.因此，枢纽集散平衡和干线对流平衡问题值得深入研究和探索.轴辐式网络在国外的研究较早，于上世纪七十年代提出，Gordon和Neufville指出在连接相同数目的营业中心时，轴辐式网络可大大减少直接相连的路线数，网络较直通且更经济.枢纽点选址最初由O’Kelly[1]提出的，他提出连续枢纽点选址问题，并设计基于Weiszfeld的启发式算法.此后，离散选址方面，O’Kelly[2]提出了轴辐式网络枢纽设施选址和网络设计模型.Yaman[3]在2009年提出了层级轴辐式网络设计问题，分析枢纽点的容量限制和交货时间约束等因素对枢纽点选址的影响.Correia等[4]基于传统枢纽点选址问题，综合考虑枢纽点的能力以及各枢纽点的需求平衡，评估需求平衡影响选址问题最优解的可能性.Alumur等[5]分别考虑建站成本和需求的不确定性，构建出单分配和多分配枢纽点选址的通用模型.Ishfaq和Sox[6]提出基于枢纽延误的多式联运物流网络设计，分析枢纽点的卸货、整合和装载等作业对网络的影响，建立在确保服务时间要求一致性的基础上，以物流网络的成本最小化为目标的模型.

国内，翁克瑞和杨超[7]分析轴辐式物流网络的形式和优缺点，指出该网络设计应考虑三个问题：规模效益、确定枢纽点数量与选址、分配物流需求节点与运输路线.胡青蜜和胡志华[8]研究了不确定或留的轴辐式网络设计的随即规划模型，并设计综合评价指标研究不确定性货流的影响.崔小燕等[9]针对无容量约束的单分配轴辐式物流网络设计的特点，建立了单分配P-枢纽中位模型，并提出一种基于蚁群算法的启发式算法.翁克瑞[10]考虑轴辐式物流网络中的轴线固定成本的问题，设计了HNDFHAC混合整数规划模型和拉格朗日松弛算法，并且在扩展问题中引入了“绕道约束”.胡青蜜等[11]考虑了不确定性O-D流需求下的轴辐式网络资源均衡利用问题，建立了不确定OD流需求的物流网络混合整数规划模型，通过调整枢纽点布局以提高网络资源均衡利用率.虽然胡青蜜等[11]也考虑到了干线运输平衡的约束，但是并没有考虑不同平衡系数下的选址及指派问题.姚志刚等[12]为证明“轴—辐”式运营网络有独立于密度经济而存在的范围经济， 在假设运输网络密度收益不变的前提下建立了独立分段运营与整合运营两种模式下运输网络的成本函数， 对比发现，当采用“轴—辐”式整合运营模式且运输网络达到最佳运营结构时才能实现范围经济.

虽然二级轴辐式网络的以往研究较多，但对二级轴辐式物流网络中的枢纽集散平衡和干线对流平衡问题却少有深入的研究，这为本文研究工作的展开奠定了基础.本文在以上研究的基础上，考虑二级轴辐式网络枢纽集散平衡和干线对流平衡这两个因素，考虑不同枢纽点数量及不同平衡系数下的二级轴辐式网络问题，采用混合整数规划方法进行二级轴辐式网络的布局决策，从中选出最佳的枢纽点位置以及二级节点的指派.

1 问题定义与分析

1.1 二级轴辐式零担物流网络概述

轴辐式物流网络(Hub-and-Spoke Logistics Network)又称中枢辐射式物流网络，是相对直通式物流网络的一个概念，该网络是一种由许多O-D流(Origin-Destination，即从起点到终点的运输流)与若干枢纽点构成的运输网络，网络一般要求每条O-D流汇聚于一个或两个枢纽点后到达终点，最终形成枢纽点之间集中流动的规模效益，进而节约系统的流动成本.相比直通式物流网络，轴辐式物流网络具有规模效益、促进物流资源整合、推动第三方物流的发展、减少运输工具等众多优点，但也带来绕道运输成本、节点成本、增加等待时间等缺点[13].

二级轴辐式网络作为轴辐式网络的基础，包括枢纽点(即一级集散点)、二级集散点、枢纽点间的干线运输、二级集散点与枢纽点之间的支线运输四个组成部分，二级轴辐式零担物流网络构成如图1所示.

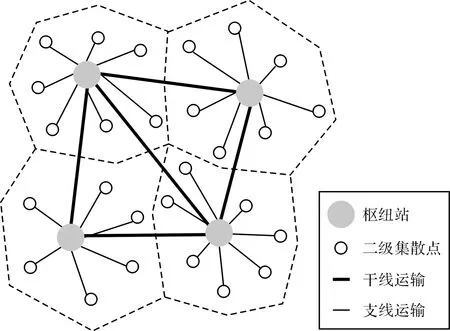
图1 二级轴辐式零担物流网络Fig.1 The bi-level hub-and-spoke less-than-truckload logistics network

该轴辐式网络是将各节点的O-D需求通过枢纽点配送到其他节点，借助枢纽点实现货物的整合，通过枢纽点之间的干线运输实现运输的规模效益，再进行货物的分拣、装卸搬运、配送等作业，最终送往各节点，完成节点间的O-D流.二级轴辐式网络设计，就是在二级集散点之间O-D需求的基础上，确定二级集散点之中确立枢纽点的位置，以及将二级集散点分配给选中的枢纽点.

二级轴辐式网络主要包括两类成本：1)枢纽点的成本.二级轴辐式网络需要建立枢纽点，必然会产生枢纽点的建造成本，以及各枢纽点的整合、分拣、组配、装卸搬运等人力成本，这部分成本往往在网络中所占比重较大.2)货物的运输成本.运输成本主要包括两方面成本：①枢纽点与二级集散点之间的支线运输成本.各二级集散点之间的货物流动需要通过枢纽点完成，因此首先必须运往枢纽点整合运输或者由枢纽点分拣后配送到各节点；②枢纽点与枢纽点之间的干线运输成本.各二级集散点的货物在枢纽点整合后，通过干线运输形成运输规模经济效益.

1.2 枢纽集散平衡分析

枢纽点作为轴辐式网络的轴心，枢纽承担着货物中转与整合的任务，枢纽资源容量的确定，与该枢纽的货物聚集量和货物发散量有重要的关系.而本枢纽点下各二级集散点通过枢纽点聚集量和发散量是一样，并且通常只占用枢纽点资源的小部分容量.而枢纽资源的大部分容量是通过干线运输聚集的.当其他枢纽点的货物通过干线运输到达该枢纽点时，放到该枢纽点进行拆装，等待发散到各二级集散点，同时把该枢纽点聚集的.当其他枢纽点的货物通过干线运输到达该枢纽点时，放到该枢纽点进行拆装，等待发散到各二级集散点，同时把该枢纽点聚集起来的货物运往其他枢纽点，如此循环往复，保证整个轴辐式零担物流网络的有效运转.这也是现今快递行业发展的主流趋势.

在枢纽点物资聚集和发散的过程中，存在一个问题，就是聚集量和发散量的不均衡，比如聚集到某枢纽点的容量为1 000单位，而由该枢纽点发散到其他枢纽点的量仅为200单位，如此，则该枢纽点资源容量为1 000单位，此时在其他枢纽点货物未聚集到该枢纽点前，枢纽点资源大部分处于闲置过程中，导致了一定的浪费.如果经过调整二级集散点的分派，使得该枢纽点的聚集量和发散量之间的差距缩小，保证枢纽点的资源得到充分利用.因此，在二级轴辐式零担物流网络的设计过程中，应该考虑枢纽集散平衡的影响，保证仓储资源的有效利用.

1.3 运输规模经济及干线对流平衡分析

枢纽点作为货物集散点，通过枢纽点整合资源后，需要通过干线运输将该枢纽点的货物运至其它枢纽点，接着返程运送货物至原枢纽点.在现实中，干线运输规模较大，运输商通常会根据承运量多少给予一定的价格折扣.仿真算例中为了模拟零担物流运输场景，假设运输量在(0，A]范围时，干线运输没有折扣，因为运输规模相对较小.而当运输量在(A，2A]时，由于运输规模的增加，干线运输可享受5%的价格折扣，依此类推.当运输规模到达一定程度后，由于运输成本等因素，运输的规模折扣不再增加，如图2中，当运输量为(5A，6A]时，单位干线运输成本为支线运输的75%，而当运输量继续增加时，单位运输成本不再减少.

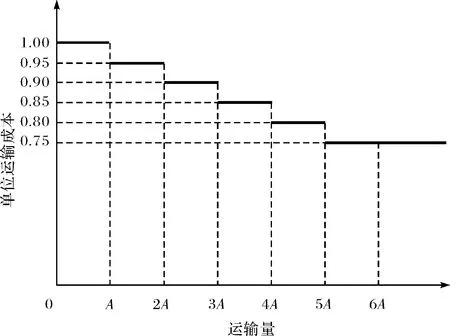
图2 干线运输规模经济说明图Fig.2 The illustration of scale economy of trunk transportation

由于干线运输的规模经济，使得更多的货物通过枢纽点的集散中转到达最终目的点.然而，枢纽点间的干线运输量往往不均衡，使得返程车辆空载或者装载率不高，这种不合理运输，造成运输资源的严重浪费.干线对流平衡指枢纽点之间往返货物的流量平衡.干线运输占据整个运输流量的大部分，如何保证干线之间的对流平衡，最大限度的降低空载率，充分利用资源，是二级轴辐式物流网络的一个重要问题.当然，实际中要做到完全的干线对流平衡是不可能的，只需要限定干线对流平衡满足一定的条件.

2 模型

2.1 模型假设及符号说明

根据上面的问题分析，该二级轴辐式物流网络的构建需要满足以下假设：各节点间的距离以欧式距离计算；节点和枢纽点间的单位流量运输成本相同；允许所有的O-D 流可以任意采取单点中转、两点中转的运输路线，但两个二级集散点间不能直通运输；每个二级集散点有且仅为一个枢纽点所覆盖.

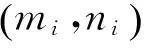
3)Ωk为枢纽点k的固定成本；Oi表示从节点i流出的量；Di表示流入节点i的量.

4)a为枢纽点k与枢纽点l之间O-D流的规模效益折扣；b为节点与枢纽点间的单位流量运输成本；p为所建枢纽点的数量.

5)yi，k，l为决策变量，表示从节点i流经枢纽点k与枢纽点l的流量；xi，k为0-1变量，等于1表示节点i指派给枢纽点k，否则为0.

2.2 二级轴辐式零担物流网络模型

根据上面的模型假设及符号说明，这里构建一个二级轴辐式零担物流网络基本模型，从各候选点中选出一些枢纽点，并将剩余的节点指派给选中的枢纽点，通过枢纽点的资源整合，完成物流网络各节点间的O-D流转移，使整个轴辐式零担物流网络物流成本最少.

[M1]: minf=f1+f2+f3，

(1)

式中，

(2)

f2=∑i，k，labyi，k，lDk，l，

(3)

f3=∑kΩk·xk，k;

(4)

s.t．

∀i:∑kxi，k=1，

(5)

∀i，k:xi，k≤xk，k，

(6)

∑kxk，k=p，

(7)

∀i:Oi=∑jHi，j，

(8)

∀j:Di=∑jHj，i，

(9)

∀i，k:∑lyi，k，l-∑lyi，l，k=

Oixi，k-∑jHi，jxj，k，

(10)

∀i，k:∑lyi，k，l≤Oixi，k，

(11)

∀i，k:∑lyi，k，l≥xi，k，

(12)

∀i，k，l:yi，k，l≥0.

(13)

式(1)～(13)定义了轴辐式零担物流网络的基本模型[M1].式(1)是模型的目标函数，使得零担物流网络的总物流成本最小，该成本由三部分成本构成，包括枢纽点与二级集散点间的支线运输成本，枢纽点间的干线运输成本，以及枢纽点的建站成本(式(2)～(4)).约束式(5)保证每个二级集散点为枢纽点或者指派给一个枢纽点；式(6)限制每个二级集散点只能被指派给选中的枢纽点；式(7)表示枢纽点数量为p；式(8)和(9)表示流出和流入节点i的流量；式(10)～(12)表示决策变量yi，k，l与xi，k之间满足的约束条件；式(13)约束决策变量yi，k，l的取值.

2.3 考虑枢纽集散平衡的二级轴辐式物流网络模型

在二级轴辐式物流网络模型的基础上，增加决策变量rk表示枢纽点k的货物聚集量，sk表示枢纽点k的货物发散量，α为枢纽集散平衡系数.为便于对枢纽资源利用情况进行分析，这里引入枢纽集散平衡综合度φ的定义，用于表示整个网络中的枢纽集散平衡综合度.基于枢纽集散平衡的二级轴辐式物流网络模型[M2]如式(2)～(18)所示.式(14)与式(1)一样；式(15)和(16)分别表示各枢纽点的货物聚集量和发散量；式(17)～(18)表示枢纽集散平衡所满足的约束条件；式(19)定义枢纽集散对流平衡综合度.

[M2]： minf=f1+f2+f3;

(14)

s.t．

式(2)～(13),

∀k:rk=∑i，lyi，l，k,

(15)

∀k:sk=∑i，lyi，k，l,

(16)

(17)

∀k：Ξk≤α,

(18)

(19)

2.4 考虑干线对流平衡的二级轴辐式物流网络模型

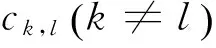
[M3]: minf=f1+f3+f4,

(20)

s.t.

(21)

式(2)，(4)-(10),

(22)

(23)

∀k，l，k≠l：Ψk，l≤β,

(24)

(25)

3 仿真算例

3.1 参数设置及试验场景设计

根据上述模型，本章通过具体的算例进行仿真分析.本算例选取了16个节点，由Excel随机生成范围在[1，50]之间的整数作为各节点的横纵坐标值.各节点间的O-D流值随机取自区间[1，99]，各节点的固定成本随机取自区间[10，12](单位：104元).此外，枢纽点之间流动产生的规模效益折扣a=0.75，节点与枢纽点间的单位流量运输成本b=1元.试验场景设计如表1所示.

表1 试验场景Tab.1 Experiment scenarios

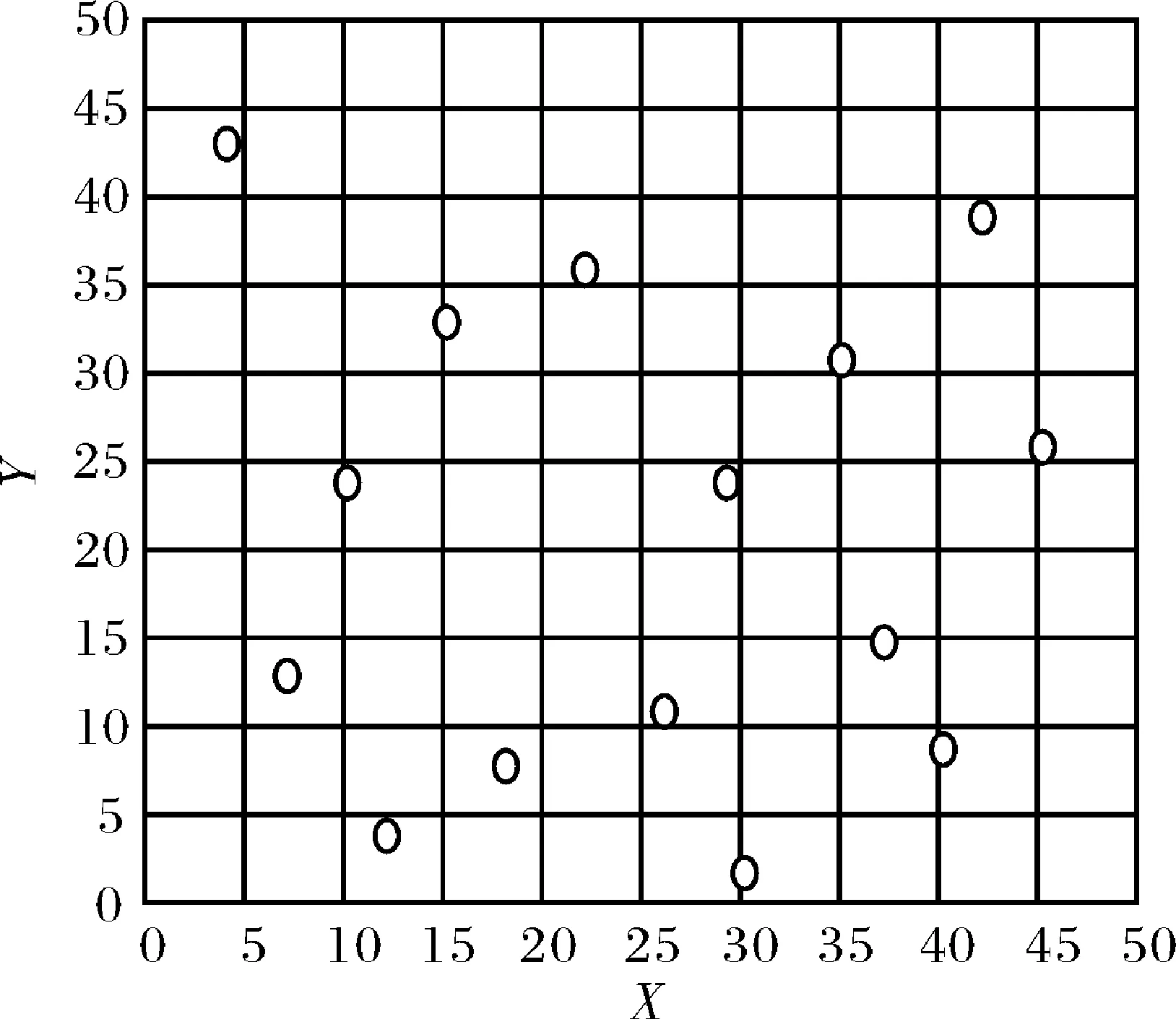
图3 p=3且不考虑平衡时枢纽点选择及指派方案Fig.3 The selection of hub and scheduling plan when p=3 without considering equilibriums

表2p=3且不考虑平衡时各枢纽点集散量及干线运输量

Tab.2Thecollectionanddistributionvolumeofeachhubwhenp=3withoutconsideringequilibriums

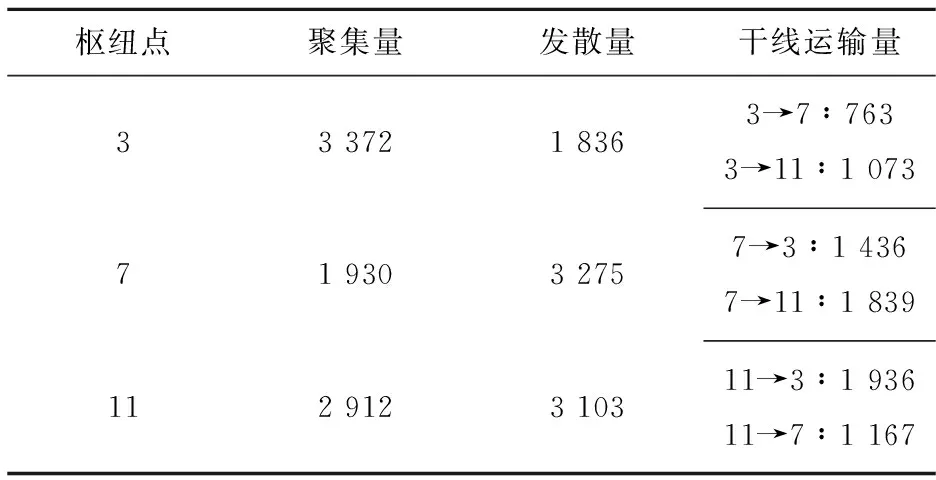
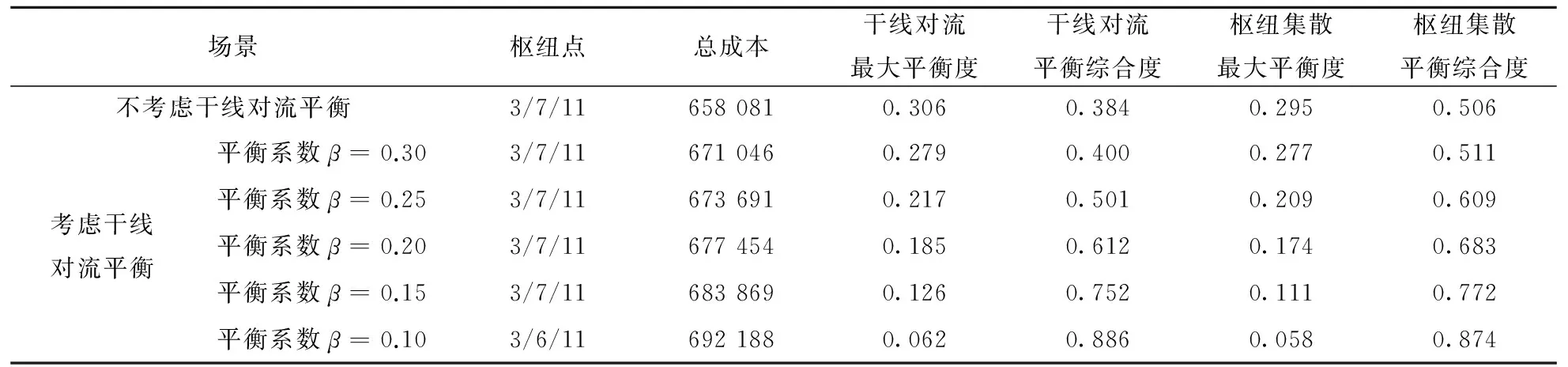
表3 p=3时不同平衡系数下的干线对流平衡结果Tab.3 The results of convective of trunk under different equilibrium coefficients when p=3

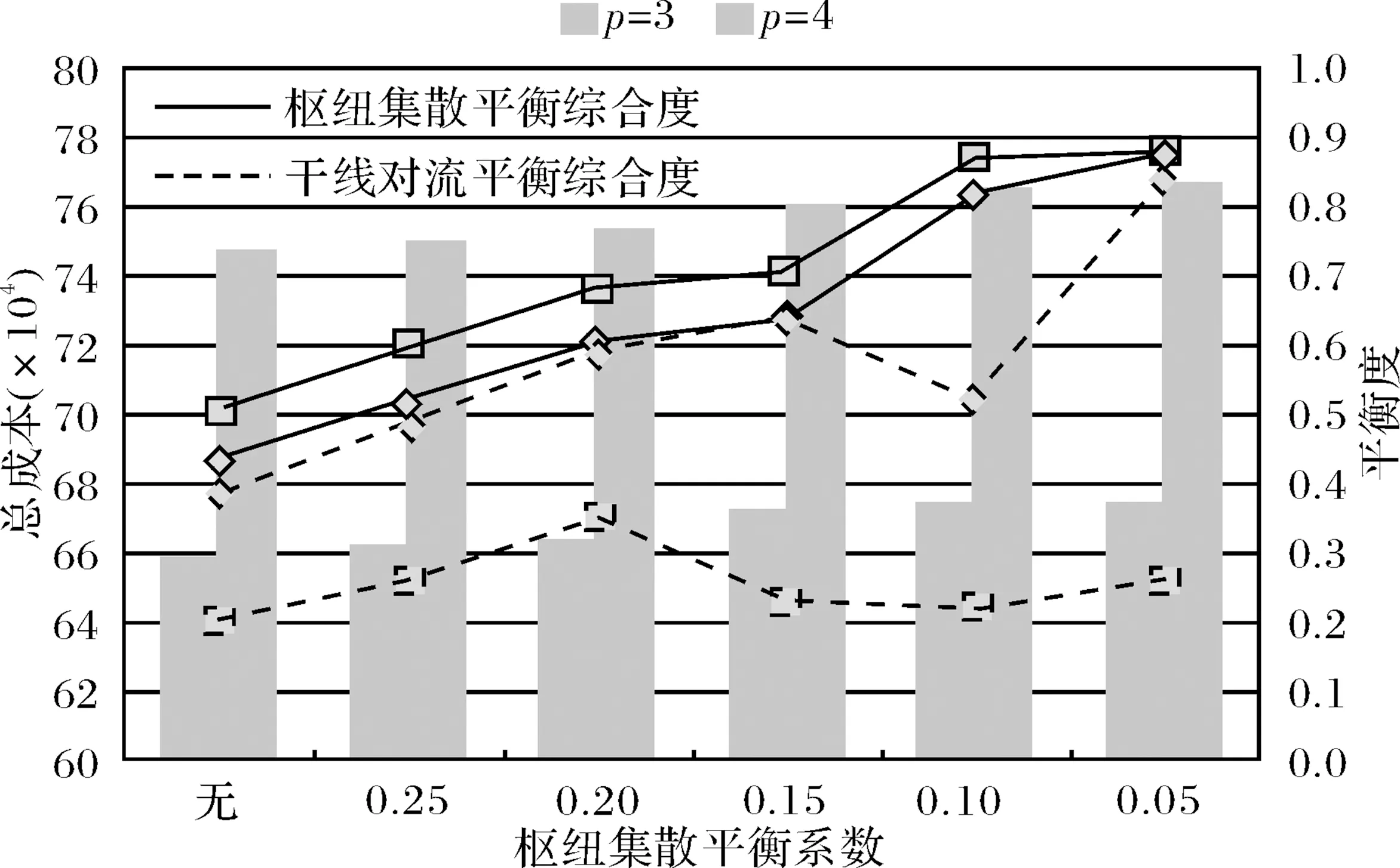
图4 不同枢纽集散平衡系数下的结果Fig.4 The results of the collective and distributive of hub under different equilibrium coefficients

3.2 试验结果分析

根据上节的试验可以得到以下结论：

1)由图3可以看出当枢纽点数量p=3且不考虑平衡时，选择节点3、7、11作为此轴辐式网络的枢纽点，此时整个网络的物流成本最少，为658081元.在表3中，枢纽点11的聚集量和发散量相对均衡，而枢纽点3和7的集散量差距较大，根据式(14)计算出来的枢纽集散平衡度分别为29.5%和25.8%.而在干线运输上，3条干线往返运输量差距均较大，根据式(18)计算出来的干线对流平衡度分别为30.6%、28.7%和22.4%.由此可见，在这种轴辐式网络布局下，枢纽集散量和干线对流量均存在较大程度的不平衡，有待改进.

2)在不同平衡系数要求下，枢纽点位置发生轻微的变动，但基本处于整个网络的中心位置，而且枢纽点间的距离比较近(如本算例的枢纽点3、7和11).这是因为在该网络中枢纽点必须覆盖所有二级集散点，干线间的流量占据很大部分，通过干线运输的规模经济尽可能的减少运输成本.

3)在图4中，当考虑枢纽集散平衡时，随着平衡系数的不断增加，不管p=3还是p=4时，网络总物流成本均有小幅增长.枢纽点数量p=3比p=4的总成本少，说明在本算例中枢纽点的固定成本作为网络中的重要成本，对网络布局规划有着重大的影响.此外，枢纽集散平衡综合度随着系数增大而明显地增加，各枢纽点的资源得到了充分的利用.当p=3时，网络的干线对流平衡综合度总体也是增加的(除了α=0.10)，而当p=4时，干线对流综合平衡度均在20%到40%之间，说明枢纽点越多，各枢纽点间的干线运输量更不易于控制，运输资源并没有得到有效的利用.

4)在表3中，当不考虑干线对流平衡时，所有二级节点会分配给离其最近的枢纽点，而较少考虑干线间往返运输流量问题.考虑干线对流平衡时，随着对平衡要求越高(即平衡系数越小时)，干线间的运输量明显增大，运输成本不断增加，但是增加幅度不大，而干线平衡综合度却明显增加，枢纽集散平衡综合度也随之增加.

综合算例分析，考虑枢纽集散和干线对流平衡时，随着平衡程度的不断提高(即系数的不断降低)，枢纽集散和干线对流平衡综合度均可达到将近90%，网络资源利用率达到一个较高的水平.然而，实际的网络设计中枢纽容量大小会对枢纽集散和干线对流平衡综合度产生影响，这个因素在算例中没有覆盖，后面的研究中需要考虑枢纽容量这个影响因子.

4 结论

随着社会的发展，轴辐式的零担物流网络在社会中的作用越来越突出.轴辐式网络中枢纽集散和干线对流的平衡，对于提高资源利用率以及降低车辆空载率意义重大.本文考虑到网络中枢纽点集散平衡和枢纽点间干线对流平衡对网络设计的影响，建立二级轴辐式零担物流网络混合整数规划模型，并进行算例仿真分析.算例结果表明，当不考虑平衡时，网络资源有较大的浪费，而随着平衡程度要求不断提高，网络运营总成本有所上升，枢纽集散及干线对流平衡综合度明显增加，网络资源得到均衡利用.接下来的研究可以从以下方面进行：最优的平衡度值的选择；枢纽点的容量限制对网络布局的影响以及同一枢纽点下运输线路优化问题.

[1]O’KellyME.Thelocationofinteractinghubfacilities[J].TransportationScience， 1986， 20(2): 92-106．

[2]O’KellyME.Aquadraticintegerprogramforthelocationofinteractinghubfacilities[J].EuropeanJournalofOperationalResearch， 1987， 32(3): 393-404．

[3]YamanH.Thehierarchicalhubmedianproblemwithsingleassignment[J].TransportationResearchPartB:Methodological， 2009， 43(6): 643-658．

[4]CorreiaI，NickelS，Saldanha-da-GamaF.Hubandspokenetworkdesignwithsingle-assignment，capacitydecisionsandbalancingrequirements[J].AppliedMathematicalModelling， 2011， 35(10): 4841-4851．

[5]AlumurSA，NickelS，Saldanha-da-GamaF.Hublocationunderuncertainty[J].TransportationResearchPartB:Methodological， 2012， 46(4): 529-543．

[6]IshfaqR，SoxCR.Designofintermodalnetworkswithhubdelays[J].EuropeanJournalofOperationalResearch， 2012， 220(3): 629-641．

[7] 翁克瑞， 杨 超. 顺应潮流的轴辐式物流网络[J]. 物流技术， 2006(7): 14-16．

[8] 胡青蜜， 胡志华. 考虑不确定货流及其影响的轴辐式网络随即规划模型[J]. 华中师范大学学报: 自然科学版， 2014， 48(2): 197-205．

[9] 崔小燕， 李旭宏， 毛海军， 等. 无容量约束单分配轴辐式物流网络设计[J]. 交通运输系统工程与信息， 2010， 10(5): 175-181．

[10] 翁克瑞. 带固定轴线成本的轴辐式网络设计问题[J]. 运筹学学报， 2012， 16(1): 88-96．

[11] 胡青蜜， 胡志华， 陶 莎. 二级轴辐式零担物流网络设计的资源均衡利用[J]. 公路交通科技， 2013, 30(4): 124-131.

[12] 姚志刚， 周 伟， 王元庆. “轴-辐”式运输网络的范围经济问题[J]. 交通运输系统工程与信息， 2009， 9(1): 24-27．

[13] 翁克瑞. 轴辐式物流网络设计的选址与路线优化研究[M]. 西安: 电子科技大学出版社， 2009．

Bi-level Hub-and-spoke LTL logistics network design based on the equilibrium of collection-and-distribution of Hub and convective flows of trunk

GAO Chaofeng1， LIN Qingfu1， HU Zhihua1，2

(1.Logistics Research Center， Shanghai Maritime University， Shanghai 201306;(2.School of Economics and Management， Tongji University， Shanghai 200092)

To cope with the unbalanced use of network resources of less-than-truckload (LTL) logistics network design， the significances of the collective and distributive equilibrium of hub and convective equilibrium of trunk are analyzed， and mixed integer programming models are established. Experiment studies show that when considering the two equilibriums， the comprehensive degree of the collective and distributive equilibrium of hub and convective equilibrium of trunk can almost up to 90% with the increasing of balance degree， which indicate that considering collection-and-distribution of hub and convective flows of trunk comprehensively can achieve a balanced use of network resources.

less-than-truckload logistics network; collections and distributions of hub; convective flows of trunk; equilibrium; mixed integer programming

2015-01-03.

国家自然科学基金青年基金项目(71101088)；国家自然科学基金项目(71471109)；上海市曙光计划项目(13SG48)；上海市教委科研创新项目(14YZ100)；交通部应用基础研究项目(2015329810260)；上海海事大学研究生创新基金资助项目(GK2013024).

1000-1190(2015)04-0551-06

U492. 3< class="emphasis_bold">文献标识码： A

A

*E-mail: gaochaofeng2007@126.com.