一类复杂网络系统的有限时间混沌同步

毛北行， 王东晓

(郑州航空工业管理学院 数理系， 郑州 450015)



一类复杂网络系统的有限时间混沌同步

毛北行*， 王东晓

(郑州航空工业管理学院 数理系， 郑州 450015)

研究了一类复杂网络系统的有限时间混沌同步问题，根据有限时间稳定性理论设计了控制器，能够使驱动网络与响应网络达到有限时间同步，同步误差按预设的指数速率收敛，得到了误差系统渐近稳定的充分性条件．

混沌； 复杂网络； 有限时间同步

人们对复杂网络的研究已经渗透到很多领域，并取得了丰硕的结果[1-6]. 文献[7]提出了系统的有限时间控制问题，文献[8]提出了有限时间有界的概念，从而将有限时间稳定性的概念拓展的更具一般性，文献[9]研究了离散奇异系统的有限时间控制问题，文献[10]研究了一类不确定线性离散系统有限时间观测器设计，上述文献讨论的都是离散系统的有限时间稳定性问题，文献[11]研究了供应链网络系统牛鞭效应的有限时间控制问题，文献[12]研究了一类脉冲切换系统的有限时间稳定性问题，文献[13]研究了Lurie混沌系统的有限时间同步问题，但上述文献研究的都不是复杂网络的有限时间同步控制问题，而关于复杂网络的有限时间混沌同步方面的的文章并不十分多见，本文基于自适应控制方法研究了复杂网络混沌系统的有限时间同步控制问题，得到了误差系统渐近稳定的充分性条件．

1 主要结果

考虑如下复杂网络混沌系统：

(1)

(2)

以系统(2)为响应系统，定义系统误差为：

则容易得到：

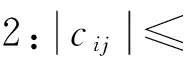
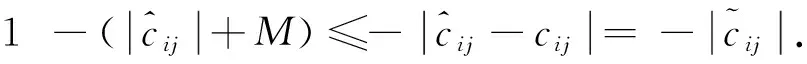
引理2[14]考虑如下n维方程

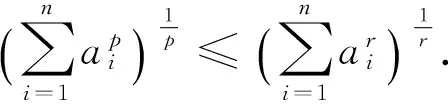
定理1选择控制器

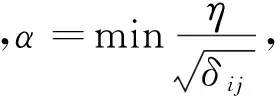
进一步根据引理1和引理3，容易得到

2 数值算例

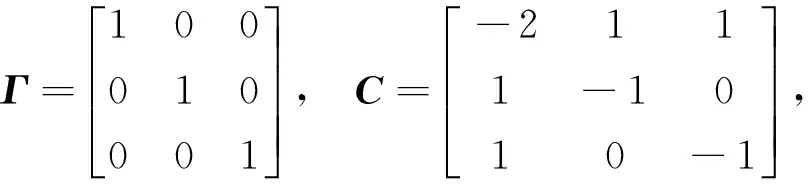
驱动系统如下：

响应系统为：

定理1对应的控制器为：

系统的初始值为

xi(0)=(1+0.5i，-1+7i，2+5i)，

yi(0)=(-1+i，1+2i，3i)，

η=1，δij=1，li=10，M=10.

系统的误差曲线如图1 所示，从图1中可以系统的看出，网络在耦合初期， 误差随时间演化的差异十分明显，经过一个暂态过程后，误差变量随时间演化趋于零，混沌同步得以实现，同步时间T<0.20s．

3 结论

基于自适应方法研究了复杂网络混沌系统的有限时间同步控制问题，得到了误差系统渐近稳定的充分性条件，并给出了同步时间的估计.而具有非线性耦合的有限时间同步问题是需要进一步研究的问题.

[1] 方 洁， 胡智宏， 江 泳. 耦合混沌系统自适应修正函数投影同步[J].信息与控制， 2013， 42(1)：39-45．

[2] 吕 翎，李 纲，张 檬.等. 全局耦合网络的参数辨识与时空混沌同步[J].物理学报， 2011， 60(9)：5051-5056．

[3] 李德奎，张建刚.时滞和非时滞耦合的驱动响应动态网络的函数投影同步[J].太原理工大学学报， 2013， 44(2)：162-168．

[4] 卞秋香，姚洪兴. 复杂网络的线性广义同步[J].系统工程理论与实践， 2011， 31(7)：1334-1340．

[5] Mei J， Jiang M， Wang J. Finite-time structure identification and synchronization of drive-response systems with uncertain parameter[J].Commun Nonlinear Sci Numer Simulat， 2013(18): 999-1015.

[7] Dorato P.Short time stability in linear time varying system[C]//In Proc International Convention-on Record Part 4，1961: 83-87．

[8] Amato F， Ariola M， Abdallah C T ，et al.Danamic output feedback finite-time control of LTI Systems subject to parametric uncertainties and disturbances[C]//In Proc European Control Conference， Kals-ruhe 1999: 1176-1180．

[9] 黄 发，吴保卫.离散奇异系统的有限时间控制[J].重庆师范大学学报: 自然科学版， 2012， 29(2)：51-54．

[10] 朱 琳，沈艳军. 一类不确定线性离散系统有限时间观测器设计[J].电机与控制学报， 2008， 12(1)：99-108．

[11] 李 玲，孙业国.供应链网络系统的牛鞭效应的有限时间控制[J].华东经济管理， 2013， 27(12)：105-108．

[12] 陈国培，刘晓芬，杨 莹.一类脉冲切换系统的有限时间稳定性[J].控制工程， 2012， 19(2)：218-220．

[13] 毛北行，李巧利. Lurie混沌系统的有限时间同步问题[J].四川师范大学学报， 2014， 37(4)：497-500．

[14] Bhat S P， Bernstein D S . Finite-time stability of continuous autonomuous systems[J]. SIAM J Control Optim， 2000， 38(3):751-766．

[15] Hardy G， Littlewood J， Polya G. Inequalities[M]. Cambridge: Cambridge University Press，1952．

Finite-time chaos synchronization of a class of complex networks systems based on self-adapt approach

MAO Beixing， WANG Dongxiao

(Department of Mathematics and Physics， Zhengzhou Institute of Aeronautical Industry Management， Zhengzhou 450015)

The paper studied the problem of finite-time chaos synchronization problem of a class of complex networks systems. A controller was proposed based on the finite-time stability theory. The condition was drived when two identical complex networks systems achieve the fast finite-time synchronization and synchronization time is estimated.The synchronization errors convergence according to exponential predetermined. We got the sufficient conditions for errors systems asymptotically stable．

chaos; complex networks; finite-time synchronization

2015-01-22.

国家自然科学基金数学天元基金项目(11226337)；航空基金项目(2013ZD55006)；河南省高等学校青年骨干教师资助计划项目(2013GGJS-142)；河南省科技厅基础与前沿研究计划项目(142300410410)；河南省高等学校重点科研项目(158110011).

1000-1190(2015)04-0538-03

TP273+.2< class="emphasis_bold">文献标识码： A

A

*E-mail: bxmao329@163.com.