妙用“图形的变换”,解决线段和的最值问题
2015-03-22江苏省如东县童店初级中学
☉江苏省如东县童店初级中学 李 琴
妙用“图形的变换”,解决线段和的最值问题
☉江苏省如东县童店初级中学 李 琴
中考前的备战岁月令所有的学生、家长、老师都具有一种凝重感,要在时间紧、容量大、要求高的条件下复习好,对于每一位初三数学老师来说,还真是一种高难度的挑战.基础知识系统化复习和专题化复习是中考总复习的一条主脉线,综合性模拟训练和回归教材贯穿总复习的整个过程,其中专题化复习是非常考验教师的教育智慧的.一个有着真知灼见的教师绝对不会满足课本、教参,他们的创造性教学便源于此,比如专题复习中,教师事先要通过大量的收集、整理、归纳各类问题,形成体系,方能凸显规律和方法.
著名数学家G·波利亚说过:“一个专心的认真备课的老师能够拿出一个有意义但又不太复杂的题目,去帮助学生挖掘问题的各个方面,使得学生通过这道题,就好像通过一道门户,把学生引入一个完整的理论领域.”在中考总复习中,笔者就曾经尝试以某些典型的例题为模型进行深入的挖掘,加以提炼引申,适当加工改造,培养学生思维的广度和深度,创造性地解决实际问题,以期达到以少胜多、事半功倍之效.下面笔者就借用“图形的变换”说说这个专题复习.
一、利用轴对称变换解决线段和、差的最值问题
例1已知:如图1所示,A、B两村庄在一条小河的同一侧,要在河边建一自来水厂向A、B两村庄供水,若要使厂址到A、B两村的水管最省料,厂址应设在哪个位置,为什么?
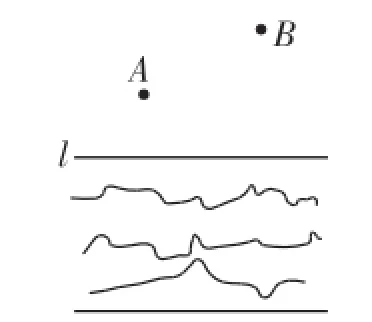
图1
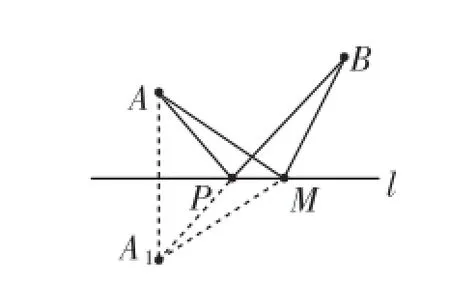
图2
具体解法:如图2,把小河抽象为直线l,作A1和A关于直线l对称,连接A1B,与直线l交于P点,厂址位于P点时,使得PA+PB最小.
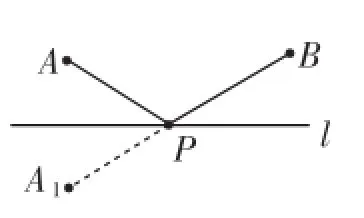
图3
思路分析:如图3,为什么P点能使得PA+PB最小呢?理由如下:如图2,在直线l上任意取一点M,连接AM、BM,由轴对称可知MA=MA1,PA=PA1,在△BMA1中,有BM+MA1>BA1,BM+MA1>BP+PA1,所以BM+MA>BP+PA,故而,厂址位于P点时,使得PA+PB的值最小.

图4
变式1:如图4,已知点A(1,5),B(3,-1),点M在x轴上,当AM+BM最小时,求M的坐标.
思路分析:如图4,连接AB交x轴于点M,设直线AB的解析式为y=kx+b,则解得所以y=-3x+8,令y=0,则-3x+8=0,解得,故M的坐标为
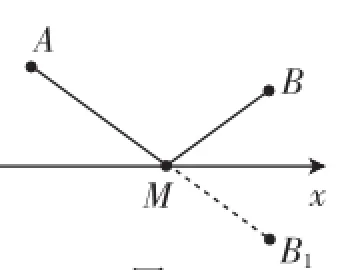
图5
变式2:如图5,已知点A(1,5),B(3,1),点M在x轴上,当AM+BM最小时,求M的坐标.
思路分析:如图5,作B和B1关于x轴对称,连接AB1,则B1(3,-1).设直线AB1的解析式为y=kx+b,则解得所以y=-3x+8,令y=0,则-3x+8=0,解得,故M的坐标为
点评与感悟:例1的理论根据是:“两点之间,线段最短”,其原理是把不在同一条直线上的线段利用轴对称转化到同一条直线上去研究的,由此可见数学上“转化与化归”这一思想的重要性.本组题从研究线段和的最值问题展开,以例1为知识的生长点,把直线同侧的两点变为异侧的两点,这两种图形都置于平面直角坐标系中进行研究,利用一次函数中的待定系数法求出函数解析式,确定与x轴的交点坐标.
例2已知点A(1,5),B(3,1),点M在x轴上,当AMBM最大时,求M的坐标.
思路分析:连接AB并延长交x轴于M点,使得AMBM最大,理由如下:
在x轴任意取一点C(假设AC>BC),在△ABC中,因为两边之差小于第三边,所以AC-BC<AB,即AC-BC<AM-BM.
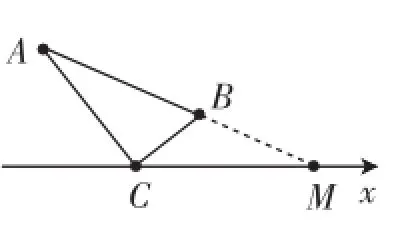
图6
点评与感悟:例2的理论根据是:“两点之间,线段最短”,其原理是把不在同一条直线上的线段利用轴对称转化到同一条直线上去研究的,数学上“转化与化归”思想的重要性不言而喻,真正起到了化难为易、化繁为简的等价转化的作用.本组题从研究线段差的最值问题展开,在例2的基础上,把直线同侧的两点变为异侧的两点,这两种图形都置于平面直角坐标系中进行研究,通过函数知识,确定与x轴的交点坐标.
二、用平移变换解决线段和的最值问题
例3如图7,A和B两地在一条河的两岸,现要在河上造一座桥MN.桥造在何处才能使从A→M→N→B的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直)
具体解法:如图8,我们可以将点A沿与河垂直的方向平移MN的距离到A1,那么为了使AMNB最短,只需A1B最短.根据两点之间距离最短,连接A1B,交河岸于点N,在此处造桥MN,所得路径AMNB就是最短路径.

图7
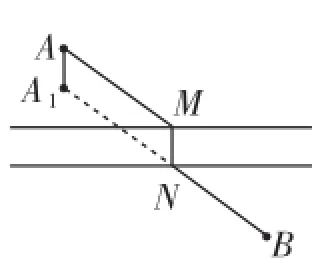
图8
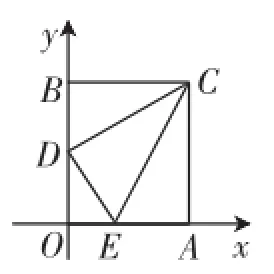
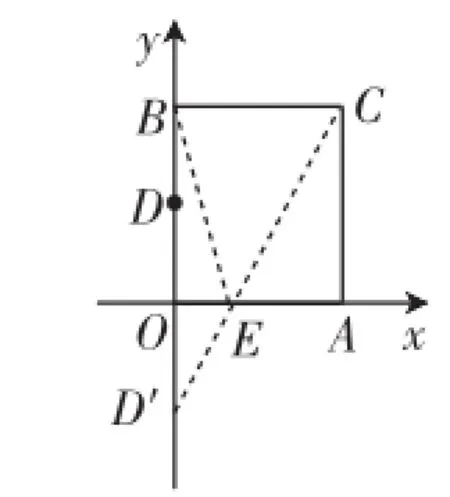
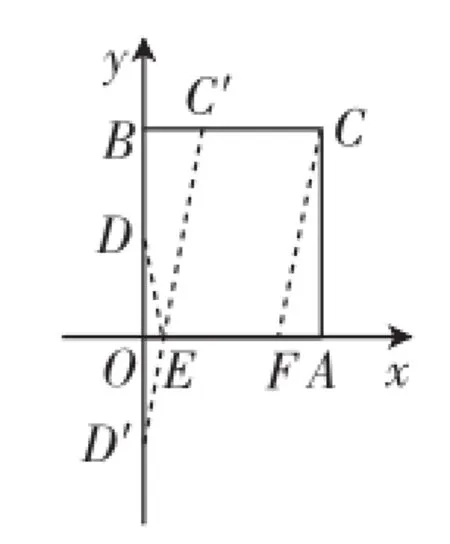
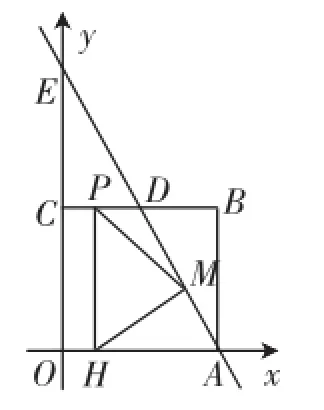
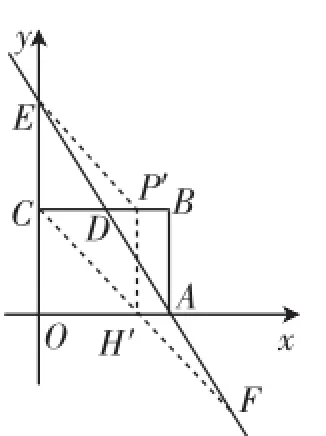
思路分析:如图7,从A到B的路径长=AM+MN+NB,由于河岸宽度是固定的,造的桥要与河垂直,因此MN的长度是固定的.要使得从A到B的路径AMNB最短,就转化为AM+BN最短的问题,不妨把MA沿MN的方向平移至NA1的位置,当A1、N、B三点共线时,AM+BN最短(或者把BN沿NM方向平移至MB1的位置,如图8,当B1、M、A三点共线时,AM+BN最短).为什么此时AM+BN最短呢?如图9,如果在不同于MN的位置造桥M1N1.由于M1N1=MN=AA1,又根据“两点之间,线段最短”可知,A1N+NB< A1N1+N1B,即AM+NB 图9 点评与感悟:这是人教版八年级数学上册中最短路径问题后的数学活动中的造桥选址问题,往年有80%的学生不能很好地理解和掌握这个问题,所以笔者认为不宜在课堂上探讨,私下感兴趣的可以进行探讨解决,但到了初三中考备战前段时间就不一样了,学生的理解力和解题能力都空前达到了一定的高度,放在本专题中讲,不仅效果好,还能起到抛砖引玉的作用. 例4在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点. (1)若E为边OA上的一个动点,当△CDE的周长最小时,求点E的坐标. (2)若E、F为边OA上的两个动点,且EF=2,当四边形CDEF的周长最小时,求点E、F的坐标. 思路分析:(1)如图10,△CDE的周长=CD+DE+EC,CD的长是固定的,当△CDE的周长最小时,也就是DE+EC最小,从而转为例1所解决的问题. 图10 具体解法:(1)如图11,作点D关于x轴的对称点D′,连接CD′与x轴交于点E. 因为OB=4,OA=3,D是OB的中点,所以OD=2,则D的坐标是(0,2),C的坐标是(3,4),所以D′的坐标是(0, -2).设直线CD′的解析式是y=kx+b,则解得则直线的解析式是y=2x-2.在解析式中,令y=0,得到2x-2=0,解得x=1.则E的坐标为(1,0). 图11 图12 思路分析:(2)如图12,四边形CDEF的周长=CD+DE+EF+FC,CD和EF的长是固定的,当四边形CDEF的周长最小时,也就是DE+FC最小;与图10进行比较,发现图10中DE和CE有公共端点E,而图12中DE和CF没有公共端点,怎样才能把图12转化为图10呢?仔细观察会发现,把线段CF向左平移2个单位使得点F和点E重合或者把线段DE向右平移2个单位使得点E和点F重合,就能把图12转化为图10进行解决了. 具体解法:(2)如图13,作出D的对称点D′,把C向左平移2个单位长度到C′,连接C′D′,与x轴的交点就是E,E点向右平移2个单位长度就是F.因为D′的坐标是(0,-2),所以C′的坐标是(1,4).设直线C′D′的解析式是y=kx+b,则解得则直线的解析式是y=6x-2.在 y=6x-2中,令y=0,解得 图13 图14 或者把D向右平移2个单位长度的D′(2,2),作出D′的对称点D″(2,-2),如图14. 因为C的坐标是(3,4),设直线CD″的解析式是y=kx+ b,则解得则直线的解析式是y=6x-14.在y=6x-14中,令y=0,解得 图15 图16 变式:如图15,在平面直角坐标系中,矩形ABCO,B点坐标为(4,3),抛物经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,点F在直线AD上且横坐标为6. (1)求该抛物线解析式并判断F点是否在该抛物线上; (2)如图16,动点P从点C出发,沿线段CB以每秒1个单位长度的速度向终点B运动;同时,动点M从点A出发,沿线段AE以每秒个单位长度的速度向终点E运动.过点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒.问EP+PH+HF是否有最小值,如果有,求出t的值;如果没有,请说明理由. (2)因为E(0,6),所以CE=CO,如图17,连接CF交x轴于点H′,过H′作x轴的垂线交BC于点P′,当P运动到P′,H运动到H′时,EP+PH+HF的值最小. 图17 设直线CF的解析式为y=k2x+b2,因为C(0,3)、F(6,-3),则解得所以y=-x+3. 当y=0时,x=3,所以H′(3,0),所以CP=3,所以t=3. 点评与感悟:本组题以例1和例3为知识的生长点,即以轴对称为基础,借助平移来解决问题的,综合性很强.把例1和例3涉及的知识点放置到函数这个情境中去研究,既用到了一次函数的知识,又用到了二次函数的知识,对学生的能力要求很高,要求学生能灵活地从复杂的情境中剥离出各种简单的基本图形,熟练地运用各种简单的基本图形去解决复杂的问题. 在本专题复习中,数形结合思想贯穿始终,数与形是数学中的两个最基本的研究对象.作为一种数学思想方法,数形结合包括两个方面:第一种情形是“以数解形”,而第二种情形是“以形助数”.著名数学家华罗庚曾说:“数缺形时少直觉,形少数时难入微,数形结合百般好,隔离分家万事休.”简简单单几句话,道尽了数形之妙.在专题复习中,尤其要重视数学思想方法的体现,就好比航海需要舵手的掌控,而解题能力尤其需要数学思想方法来指明解题的方向. 古希腊哲学家芝诺关于学习知识是这样说的:“如果用小圆代表你们学到的知识,用大圆代表我学到的知识,那么大圆的面积是多一点,但两圆之外的空白都是我们的无知面,圆越大其圆周接触的无知面就越多.”这何尝不是学生与教师关系的真实写照!科学上没有平坦的大道,真理的长河中有无数礁石险滩.只有不畏攀登的采药者,不怕巨浪的弄潮儿,才能登上高峰采得仙草,深入水底探骊得珠.“问渠那得清如许,为有源头活水来”,唯有学习,不断地学习,勤奋地钻研,有创造性地教学,才能让孩子们稳妥地踩着我们的肩膀,站得更高,看得更远.H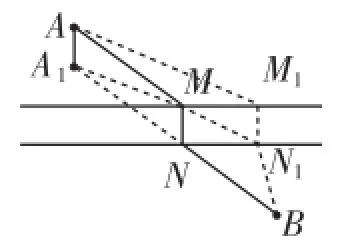
三、以轴对称变换为基础,借助平移变换解决线段和的最值