对一道无刻度直尺作图问题反例的商榷和解题思路探究
2015-03-22甘肃省天水市第七中学吴俊杰
☉甘肃省天水市第七中学 吴俊杰
对一道无刻度直尺作图问题反例的商榷和解题思路探究
☉甘肃省天水市第七中学 吴俊杰
2014年天津市中考数学中18题第二问比较新颖,具有一定难度,做过该题的教师、学生多感觉无从下手,不仅难以找到解题思路,也难以理解参考答案中的解答是如何想到的.文1、2撰文深入分析探讨了这一问题,文3对文1中的方法2是否适用于任意三角形进行了深入思考,给出了一个反例.经反复思考,笔者认为文3的结论下的有些武断.本文拟结合王华、朱玉祥两位老师的探究,介绍两种易于理解和操作的解法,并对王云峰老师文3的反例谈谈自己的商榷意见.
一、题目呈现和相关文献
如图1,将△ABC放在每个小正方形的边长为1的网格中,点A、点B、点C均落在格点上.
(1)AC2+BC2的值等于_________;
(2)请在图1所示的网格中,用无刻度的直尺,画出一个以AB为一边的矩形,使该矩形的面积等于AC2+BC2,并简要说明画图方法(不要求证明).
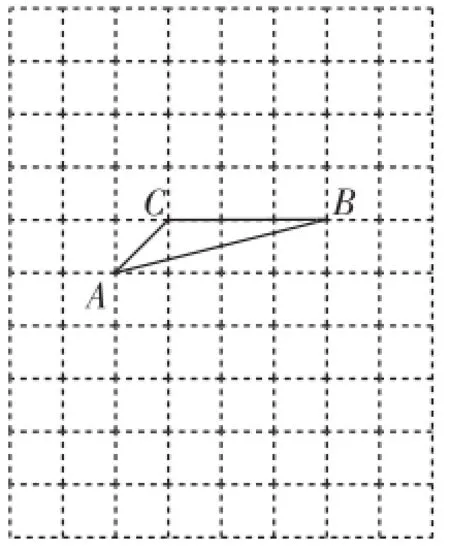
图1
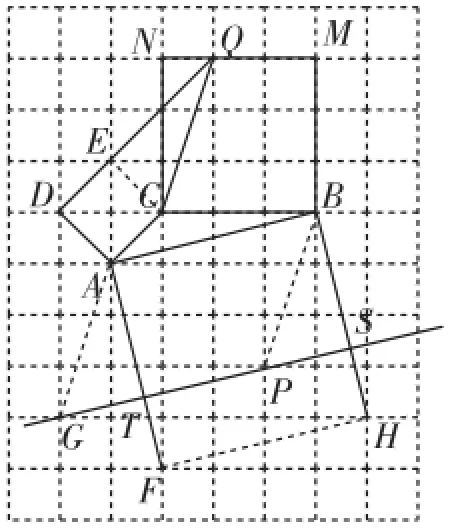
图2
(2)如图2,分别以AC、BC、AB为一边作正方形ACED、正方形BCNM、正方形ABHF,延长DE交MN于点Q,连接QC,平移QC至AG、BP位置,直线GP分别交AF、BH于点T、S,则四边形ABST即为所求.
王华老师在文1中指出,黄家礼编著的《几何明珠》一书中记载的古希腊数学家帕普斯发现的一个定理就是本题的知识背景.笔者认为王华老师“解法初探”的思路很不错,可惜思路分析中有部分内容语焉不详,理解起来具有一定的难度,且文章后半段迎合帕普斯所发现的定理而没有对最初想法做深入思考.
朱玉祥老师在文2中指出苏科版实验版数学八年级(上册)课本在勾股定理一章后安排有一道思考题:“如图3,分别以△ABC和△DEF的各边为一边向外作正方形,其中两个小正方形的面积和等于大正方形的面积吗?”从而揣测这正是本题命题的参考素材.使用该教材的地区的学生和教师解答此题可能会多少由此得到一定的解题思路的启发,但是对于使用其他教材的地区的考生、教师来说,没有了教材探究的铺垫,更没有帕普斯所发现定理的知识积累,面对此题一时难以找到解题思路也就可以谅解了.

图3
朱老师通过构造“X”型相似三角形给出了一种解答.他注意到所求矩形短边长与长边长的比是11∶17,故考虑在正方形AEDB的边AE和BD上设法找点M、N,如图4,使他通过构造“X”型相似三角形得到用同样的方法可以在BD上取点N,使,然后连接MN,则矩形AMNB就为所求的矩形.朱玉祥老师指出,由于方格纸和作图工具的局限,从点D向右取距离D点3个单位的点P,可以通过作等腰直角三角形获得.即先从点D垂直向上取距离D点3个单位的点,再沿着方格的对角顶点的方向作45°的斜线,与过D点的水平线的交点就是点P,显然DP=3,BG=5.5,所以PG与BD的交点就是点N.这是朱老师思路最精彩的地方,但也不无遗憾,一是作图方法复杂了点儿,二是图4中的作图超出了给定的格点图的范围限制.
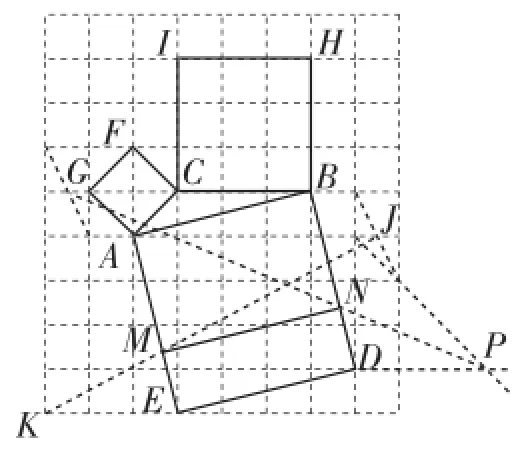
图4
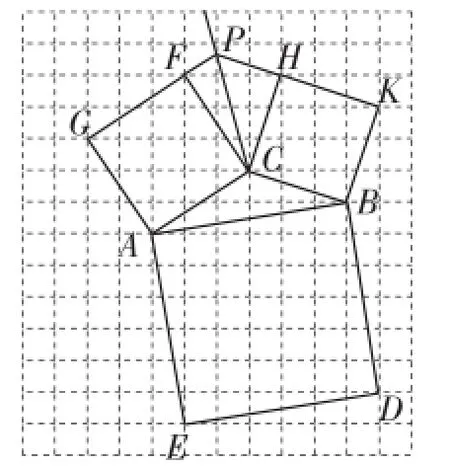
图5
王云峰老师在文3中构造了反例,如图5所给△ABC中,依据文1中的方法2,分别以AC、BC为边向外作正方形ACFG和正方形BCHK,发现边GF和HK所在的直线相交于点P,但P点不是格点.从而给出下面的判断:“由于点P不是格点,因此线段PC无法利用无刻度的直尺进行平移,后续作图步骤无法完成,因而不能画出一个以AB为边且面积等于AC2+BC2的矩形.可见,方法2不能适用于任意的△ABC.”显然这一结论下的为时太早,过于武断.
二、商榷1:文3中的反例能否利用无刻度的直尺作图
此题从表面上看主要考查应用设计与作图,但如何借助格点图分析、思考问题才是问题解决的重点.
在文3的反例中,P点不是格点,依据文1中的方法2“无法直接”平移PC到点A、B,此言不虚.但是如果认真分析图形,通过适当的推理计算,可以发现直线CP经过多个格点,因而笔者考虑,虽然线段PC无法直接利用无刻度的直尺进行平移,但是我们可以“分两步走”实现线段PC的平移.
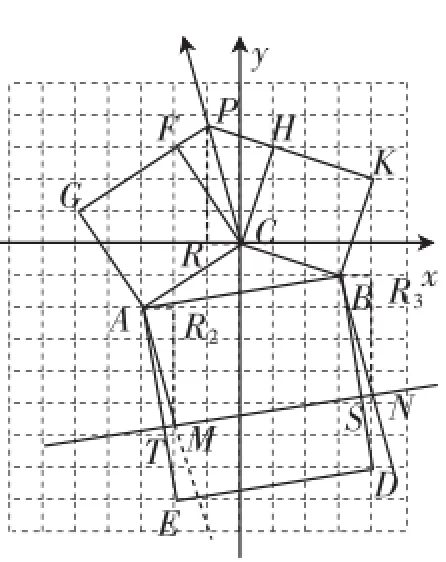
图6
为了便于后文叙述,不妨以点C为坐标原点,以经过点C的水平格线为x轴,铅直格线为y轴,如图6所示建立直角坐标系,则文3所设计的反例中,点C的坐标为(0,0),点A的坐标为(-3,-2),点B的坐标为(3,-1).依据文1中的方法2作图,可以确定以下各点的坐标:G(-5,1)、F(-2,3)、H(1,3)、K(4,2),利用待定系数法可以求得直线GF的函数关系式为直线HK的函数关系式为直线GF与直线HK的交点P为,直线CP的函数关系式为当x=-3时,y=11,所以直线CP经过格点Q(-3,11).
(1)作平行线.过A、B分别作直线PC的平行线(不妨只作射线):如图6,依据格点图的特征,只需要在建立了直角坐标系的网格图中找出格点Q2(0,-13)、Q3(6,-12),连接AQ2和BQ3,就有射线AQ2∥PC,射线BQ3∥PC.
(2)截取等长线段.在射线AQ2和BQ3上分别截出线段AM=PC,BN=PC.因为P点不是格点,无法直接使用无刻度的直尺进行测量,也就无法直接截取线段AM和BN使之与PC相等.分析图形,找到格点R(-1,0),注意到△PRC是直角三角形,因此考虑作出与△PRC全等的三角形,可以利用全等三角形对应线段相等的性质在射线AQ2和BQ3上截取AM和BN.
如图6,在网格中可以找到格点R2和R3,其坐标分别为(-2,-2)、(4,-1).连接AR2,过点R2作出铅直方向的格线与射线AQ2相交于点M,从而构造Rt△MR2A,可以证明△MR2A≌△PRC,所以AM=PC.同理,可以构造△NR3B≌△PRC,所以BN=PC.
至此,实现了无刻度的直尺平移线段的作图.依据方法2的后续步骤,连接MN与AE、BD分别相交于点T、S,四边形ABST即为所求的矩形,具体证明详见文1,此处不再赘述.
在上述作图中,虽然P点不是格点,但是笔者注意到直线CP经过格点Q(-3,11),通过寻找到格点Q2(0,-13)、Q3(6,-12)、R2(-2,-2)、R3(4,-1),采取(1)、(2)两个步骤分步走的办法,从而巧妙地解决了无刻度的直尺在文3所构造反例中作图不可能的难点.
三、商榷2:文1中的方法2能不能适用于任意△ABC
仅就文3的反例和原中考试题分析文1中的方法2是可行的,依据本文对方法2“分步走”的解答分析,可以发现解决与反例相类似问题时,能否利用无刻度的直尺作图的关键有两点:(1)在直线CP上能否找到一个除点C以外的格点Q;(2)能否找到格点R、R2和R3构造全等直角三角形.依据坐标的定义可知第二点不是问题解决的难点,真正的难点在于(1).下面通过研究一个类似于反例但具有一般性的无刻度的直尺作图问题,以探究直线CP是否经过除点C以外的其他格点.
分别以点C所在的横、纵格线为x轴和y轴建立直角坐标系,下面仅仅研究图7和图8两种情况.图7中点A、B在相邻的两个象限中,图8中点A、B在相对的两个象限中.

