习题课操作要义：精选、备题与测评——由一道QQ群里的习题研讨说起

☉江苏省如东县马塘镇邱陞中学 刘志娟

习题课操作要义：精选、备题与测评
——由一道QQ群里的习题研讨说起

☉江苏省如东县马塘镇邱陞中学 刘志娟

国庆期间，参与某初中数学教师QQ群交流一些典型几何题的解法研讨，由于群里教师较多，切磋研讨常常有很多个人思考所不及的发现，本文整理近期在群里引发热议的八年级几何习题，并给出进一步的思考，提供研讨．

一、群里的习题研讨实录

习题已知A（0，a），B（b，0），且a，b满足（a-1）2＋|b-1|＝0.

（1）求△AOB的面积；

（2）如图1，点C在线段AB上（A、B两端点除外），AD⊥AB，且∠DOC＝45°，求证：OD平分∠ADC．

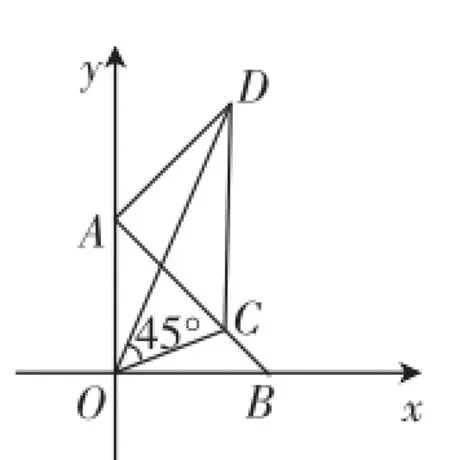
图1

说明：由于该题的题干只服务于第（1）问，是个无甚趣味的多知识点拼凑问题，引发大家展开解法探讨的是第（2）问，以下为研讨实录的观点摘录．

师1：基于直线OD对称的角度，可以构造如图2的辅助线延长DA到C′，使AC′＝BC，连接OC′，两次全等实现问题解决．

师2：图2这种思路，也可以是将△OBC绕点O逆时针旋转90°，同样能实现目的．

图2

师3：几何画板，演示如下，也可以将△OAD绕点O顺时针旋转90°，如图3，也可求证．

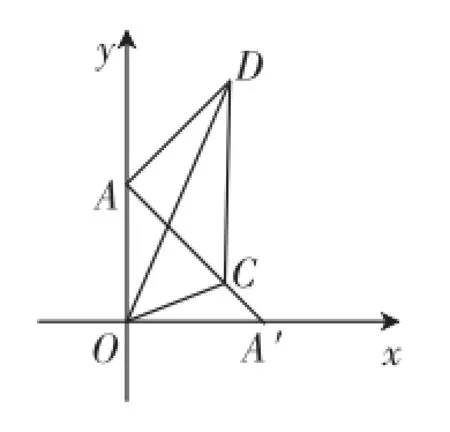
图3

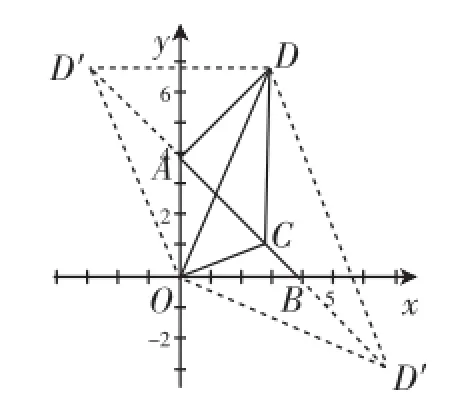
图4

师1：这个问题基于轴对称或翻折，可以得到图4，可以看清这个问题的一些“结构”．

（师1关于问题结构的揭示，引来不少网友的点赞）

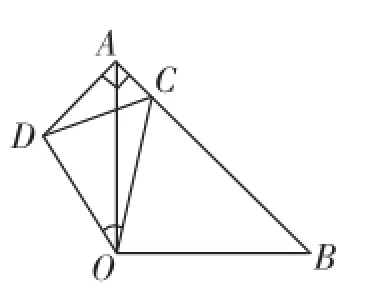
图5

师4：这道习题提出“求证：OD平分∠ADC”有待商榷，建议改为“探究∠ADO与∠CDO的数量关系”，因为这两个角的关系应该是相等或互补，前面各位探讨的都是前者，如图5，则属于互补的情况．

师5：师4的思考很深刻，引导学生在反思回顾阶段做出上述反思，才是追求了教学深度，值得学习．

二、对习题“深层结构”的进一步揭示

有了上述研讨，贯通该习题的思路已有多样的途径，然而在解题教学中与一题多解相比，多解归一显然有更为积极的意义，下面我们继续对习题进行探索，进一步揭示它的“深层结构”．

深层结构：如图6，补成正方形ABPQ，两条对角线所在直线都是该正方形的对称轴，以正方形的中心O为圆心，作⊙O与正方形的边长相交，根据圆的旋转对称性质，易知图6中，点C绕中心O逆时针旋转90°后对应着C′，此时作∠COC′的平分线交直线AQ于点D，而这也对应着之前讨论中图2的思路．

图6

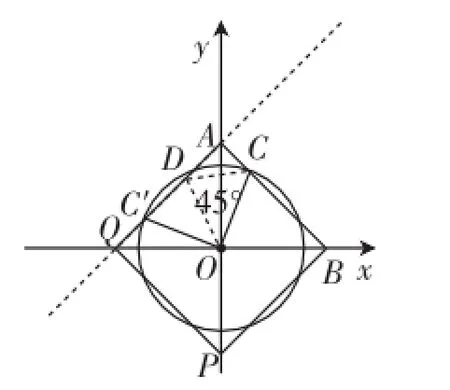
图7

再变换点C的位置，如图7，此时AC＝QC′，进一步可得∠ADO与∠CDO是互补关系．

至此，我们应该可以发现，前面所涉及的点C的位置可以看成是⊙O与正方形边的交点位置的不同，可以看成直角∠COC′的平分线交直线AQ于点D所带来的关系．

三、习题改编

当我们看清问题结构之后，问题的变式改编、拓展、推广立即成为可能，以下给出笔者的一些变式思考：

习题变式：Rt△ABC中，∠ACB＝90°，AC＝BC，点P为AB边上一点（不含AB边的中点），过点A作AQ⊥BA，且∠QCP＝45°，连接PQ．

（1）如图8，当AP＞BP时，求证：QC平分∠AQP；

（2）如图9，当AP＜BP时，探究∠AQC与∠PQC的数量关系，并说明理由；

（3）如图8，设CQ与AB交于M点，试分析AM、MP、PB之间的数量关系．（涉及勾股定理）

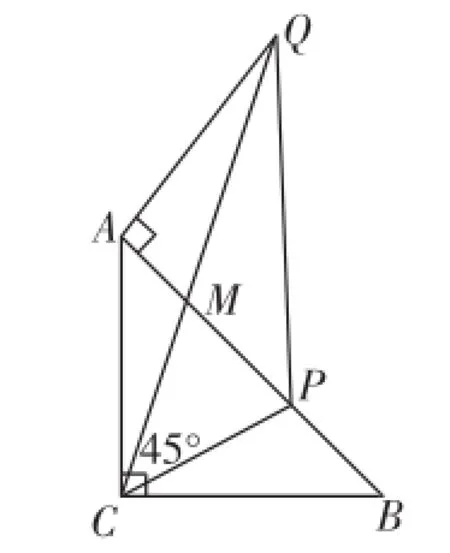
图8

图9

四、解题教学的思考

1.挑选经典考题，精心备题是上好习题课的前提

解题教学在数学教学中占有相当大的比例，然而多数解题教学常常是跟着教辅资料走，讲作业、订正错题的习题课为主，能否做到有的放矢，重点突出开展解题教学应该是努力的方向．从这个角度看解题教学，首先要挑选经典考题，再对其进行充分备题，包括思考习题的一题多解，洞察习题的深层结构，可以怎样变式、生长、拓展，这些都应该是课前认真开展的备题活动．

2.倡导对话交流，从“一题多解”走向“多解归一”

解题教学的课堂教学中，也要通过设计恰时恰点的问题启发思考，引导对话，并将问题不断引入深入，直至学生主动发现习题的一题多解，在此基础上及时组织回顾反思，鼓励学生发现问题的深层结构，理解多解归一．比如，当我们展示出习题的一种结构（如图4）后，一个必要的追问就是：点D′、A、B是否在同一条直线上？如何证明？当我们给出图6之后，也需要追问学生：OD与圆的交点是否就是圆与AB边的另一个交点？这样的辨析有助于学生对问题深层结构的认识，从而达到对问题结构的深刻理解．

3.跟踪听课反馈，讲评后设计变式习题再测评

根据多年的教学经验，我们知道，很多学生听课时似懂非懂，甚至认为自己听懂了，但听懂了并不一定会做，更不一定能讲．所以，对于经典问题、必考习题，从功利角度出发，要想追求更好的理解效果，让更多的学生能过关、会做，在听课之后进行必要的检测反馈是十分重要的．这也就是我们在上面给出变式改编试题的重要原因，在听课之后，可以安排学生限时（15～20分钟）练习变式习题，测评听课效果，笔者经常开展这样的工作，反馈检测表明，不仅有效促进了中等生对相关问题的理解，也帮助了学困生巩固了一些基础问题，同时对优秀学生提高解题效率也起到了积极的作用．

1.罗增儒．数学解题学引论［M］．西安：陕西师范大学出版社，2008.

2.中华人民共和国教育部．义务教育数学课程标准（2011年版）［M］．北京：北京师范大学出版社，2012．

3.刘东升．经历问题生成，深刻理解教材——人教八上“每日一题”的命题实践与思考［J］．中学数学（下），2014（4）．

4.夏盛亮．引导回归教材，倡导开放取向——一次县级期末卷的命题取向分析［J］．中学数学（下），2014（1）.

5.鲍建生，顾泠沅，等.变式教学研究［J］．数学教学，2003（1，2，3）．H