数形结合思想在初中数学解题中的具体应用

☉江苏省江阴英桥国际学校 吴忠妙

数形结合思想在初中数学解题中的具体应用

☉江苏省江阴英桥国际学校 吴忠妙

数学所研究的内容可以简单概括为两个方面：一是研究现实世界中的空间形式，二是研究现实世界中的数量关系.这两个方面的内容相辅相成，互相配合，实现了人类对整个世界的数学认知.因此，数学学科的研究重点也就得以确定了，即“数”与“形”.这样就引出了数学中的一个重要思想方法——数形结合.它也是初中数学教学过程中的重中之重，需要我们对之展开着重研究.

一、巧妙运用数形结合，准确理解数学概念

概念学习是数学知识学习展开的必经之路.作为基础性内容，如果概念学得不扎实，便是在学习之初为今后的深入学习埋下了隐患.因此，教师对于数学概念的教学都是比较重视的.但是由于数学概念的文字性、抽象性特征，对于概念展开生动有效的教学，并不是十分容易的.这时，我们便可以考虑让数形结合来帮帮忙.

例如，在学习过函数图像的相关概念之后，笔者发现，学生对于这部分概念理解的难点在于平面直角坐标系中横、纵坐标的含义和应用上.很多学生只是机械地背诵它们的含义，却难以将其灵活运用于数学关系的表达中.于是，笔者请学生思考这样一个问题：已知时钟在正常运行的情况下，分针每分钟转动6°，时针每分钟转动0.5°.在时钟运行过程中，时针与分针的夹角会随着时间的变化而变化.现在，设时针与分针之间的夹角是y（度），运行时间是t（分），那么，从12：00到12：30这段时间内，y与t之间的函数图像是什么？这个问题很好地将数学概念与具体图形联系起来了.学生经过认真思考得出了图像（如图1），并在这个过程中深刻领会了函数图像的内涵.

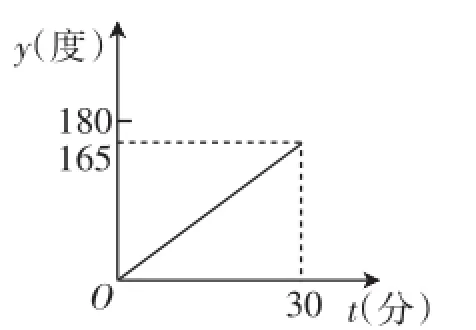
图1

二、巧妙运用数形结合，快速解答简单问题

选择、填空等问题的形式与篇幅大多短小精悍，却绝不能被师生们所忽视.如果能够快速、准确地解答简单问题，就可以为整次测验节省出可观的时间用来深入思考和检查.在解答这类问题时，数形结合一直是适用范围很广的思想方法.

例如，一个等腰梯形两组对边中点连线段的平方和是8，那么这个等腰梯形的对角线长度是_________.题目条件非常简单，可学生解答起来却不那么简单.很多学生不知道这个简短的条件该怎样分析和利用，在解题速度上卡了壳.于是，笔者提醒学生不要闲着笔，而是要边读题边画图，将已知条件翻译成具体的数学图形.学生们在一步步画出具体图形之后，思路也渐渐明晰起来了，不仅明确了题目当中所描述的数学状态，还结合等腰梯形的性质及勾股定理等知识构造了辅助线（如图2），并很快得出了答案.

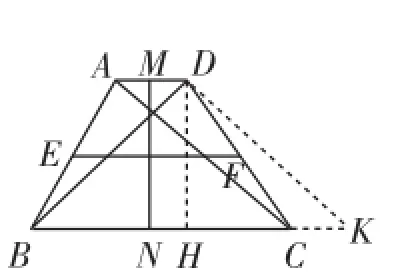
图2

可以看出，将数形结合的方式运用到简单问题的解答过程中，明显缩短了题目的解答时间，并且提高了问题解答的正确率.有了数形结合方法的辅助，很多题目都可以在短时间内迎刃而解.渐渐地，简单问题的解答甚至被学生视为一种乐趣了.

三、巧妙运用数形结合，有效建立数学模型

建模能力在数学教学中被确定为一种独立的学习能力，可见其对于数学学习之重要.它不仅要求学生们有建立模型的意识，还需要能够快速将理论知识与相应模型联系起来.不难发现，建模的过程实际上就是数形结合的真实反映.数形结合的灵活运用，自然也就成为了有效建立数学模型的关键.

例如，在一次测验中出现过这样一个问题：小林打高尔夫球，将球从山下的点O打出，使之向山顶的球洞A飞去.球的飞行轨迹可以近似视为一个抛物线，且当球达到最高处时，高度12米，其所移动的水平距离是9米.已知山坡与水平方向的夹角是30°，点O与点A间的距离是8分米，则球的飞行轨迹是什么？从题目描述中便可知道，问题的解答需要建立二次函数的模型（如图3）.另外，为了方便计算，笔者还特意指导学生对平面直角坐标系的位置选择进行了思考.

图3

四、巧妙运用数形结合，准确处理应用问题

同小学数学中的应用问题相比，初中阶段的问题难度显然提升了不少，条件也复杂了许多.为了让应用问题得到顺利解答，笔者常常会引入数形结合的方法.

例如，学生曾经遇到过这样一道应用问题：如图4，工人站在梯子上安装天花板上离地2.9m的顶灯.梯子由两个相同矩形面组成，且每个面的长被六条踏板七等分，梯脚固定跨度1m，矩形面与地面所成角α为78°.工人身高1.78m，当他的头顶距天花板0.05-0.20m时，安装起来比较方便.现在他站在梯子的第三级踏板上，安装是否方便呢？为了将这个现实场景以数学方式表现出来，笔者带领学生以图5中的方式予以呈现，解题思路瞬间明确了.

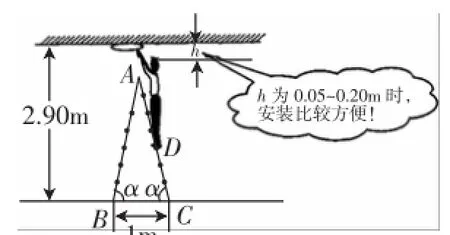
图4

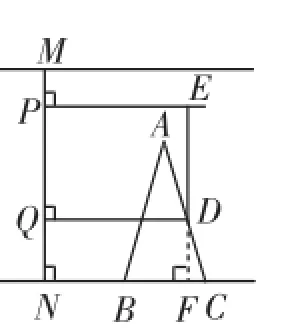
图5

很多学生在阅读过大段的应用问题叙述之后，总是一头雾水，不知所云，更不要说从中找到解答的入口了，其主要原因便在于学生没有将隐藏在文字背后的数学挖掘出来，从而无法将这些问题通过数学的思路和方法进行解决.数形结合便在这之间为学生搭建起了一座桥梁.学生们一边读题，一边画图，图形出来了，解答思路也在不知不觉中建立起来了.应用问题的解答再也不是难事了.

五、巧妙运用数形结合，顺利开展课堂活动

前文已经提到，初中数学的课堂教学中不能缺少对学生学习兴趣的激发.为了达到这个目的，笔者最为常用的方法就是开展课堂活动.活动这一形式本身就是学生所喜爱的，将要教学的知识内容融入其中，能够让学生在轻松愉悦中感知数学.在活动的触发环节，数形结合可以为我们提供很好的帮助.

图6

例如，在学习过二次函数及其图像的相关知识后，笔者向学生展示了如图6所示的图像，并且告诉大家，图中所示是二次函数y=ax2+bx+c的图像，且该图像经过（-1，1）和（2，-1）两个点.然后，笔者将全班学生分为四个“调查小组”，给每个小组布置一个“调查课题”，分别为：（1）y的最大值小于0；（2）当x=0时，y的值大于1；（3）当x=1时，y的值大于1；（4）当x=3时，y的值小于0.由学生以“调查人”的身份研究分配给本组的课题，判断其正误，各小组间不能交流提醒，看看哪组分析得又快又好.

在数形结合的过程中，教师可以尝试鼓励学生尽可能多地参与其中.在亲手将数字转变为图形的过程中，学生会扮演课堂活动的主角，从而获得最为真切的学习体验.由此，数形结合完全可以成为课堂活动开展的一个常用途径.

六、巧妙运用数形结合，推动完成深入探究

数学的思考是没有止境的，初中数学亦是如此.想要实现高质量的教学效果，我们不能满足于对课本内容本身的知晓，而是要在掌握基础知识之后进行深入挖掘和探究.灵活且深化的数学思维往往就是在这个过程中产生的.既然是深入探究，难度自然会有较大提升.为了让学生的探究活动进行得更加顺利，需要适时地巧妙运用数形结合.

从前文的论述中不难发现，数形结合对于初中数学教学的意义是十分广泛的.一方面，数形结合是数学研究的必然结果.“数”与“形”高度概括了初中数学学习中所涉及的全部内容.二者相结合，符合数学研究的科学思路，为初中数学的有效教学指明了方向.另一方面，数形结合是数学解题过程中的重要思想方法.在面对很多数学习题，尤其是条件关系比较复杂的问题时，仅仅通过代数或几何领域的单一分析是很难解决的.数形结合，是高效解题的钥匙，也是数学学习的捷径.综上所述，若广大数学教师与初中学生在学习过程中树立起牢固的数形结合意识，学习将会变得更有质量、更高效.Z