由博返约，追求简洁——一道“双曲线”综合题的命题过程

☉江苏省海安县教育局教研室 何 明

由博返约，追求简洁
——一道“双曲线”综合题的命题过程

☉江苏省海安县教育局教研室 何 明

在最近县级九年级学业水平测试命题活动中，我们设计了一道以“双曲线”为载体的综合题，测试完毕，试题被传播到网络，得到不少命题爱好者的热议，大家认为该题形式简洁、内涵丰富，是一道优秀的数学试题．本文呈现这道原创题的命题过程，并给出相关思考，供研讨．

一、命题过程

本地区使用的是人教版课标教材，反比例函数在九年级才学习，命题组拟在全卷最后的关键位置设计一道以反比例函数为载体的综合题，现给出该题的命制过程．

（1）求k的值.

（2）如图2，将∠MON绕点O旋转，射线OM始终在第一象限，交l1于点C，射线ON交l2于点D，连接CD交y轴于点Q，在旋转的过程中，∠OCD的大小是否发生变化？若不变化，求出tan∠OCD的值；若变化，请说明理由.

（3）在（2）的旋转过程中，当点Q为CD的中点时，CD所在的直线与l1有几个公共点？求出公共点的坐标．

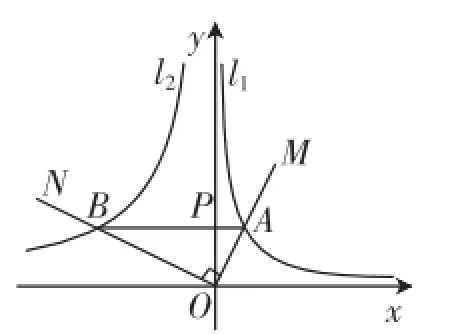
图1

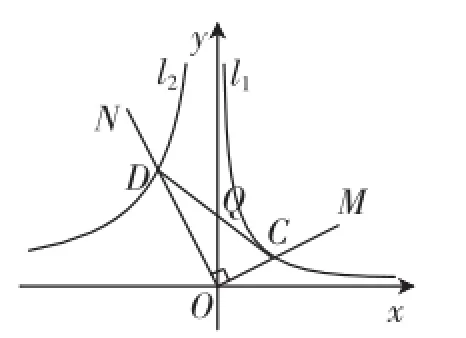
图2

由AB∥x轴，得AB⊥OP.又∠MON＝90°，则△OPA∽△BPO，则

（2）∠OCD的大小不变．

如图3，过点C作CE⊥x轴于点E，过点D作DF⊥x轴于点F.

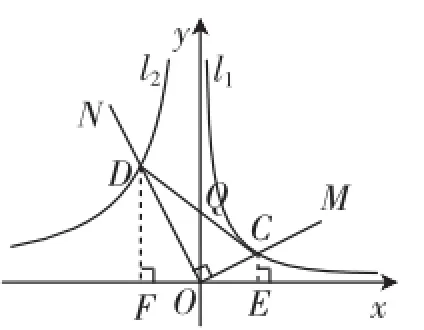
图3

（3）当点Q为CD的中点时，可得OE＝OF，结合（2）中的思考有又m>0，则m＝2.则C（2，1）、D（-2，4）．

则CD所在的直线与l1有两个公共点，分别是（2，1）

打磨意见：从第1稿及解法简述可以发现：试题涉及的知识点、数学方法很多，已达到了把关题的区分要求．然而，从试题追求简洁的角度出发，第1稿达到250个字符、包含两幅繁杂的图形，而且题干的叙述也显得啰嗦拖沓、不够简洁．经过构思，形成第2稿.

第2稿：如图4，在平面直角坐标系xOy中，射线OM、ON与曲线分别相交于点A、B，连接AB交y轴于点P．

（1）当AB∥x轴时，求△AOB的面积.

（2）如图5，当OM⊥ON时，记∠OAB＝α，∠OBA＝β．

①求证：tanα＝4tanβ；

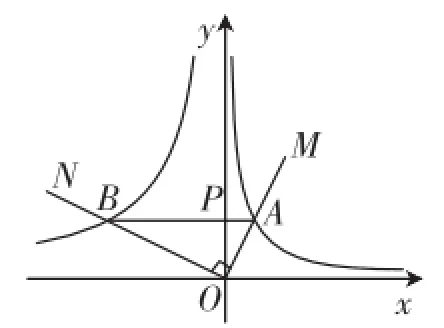
图4

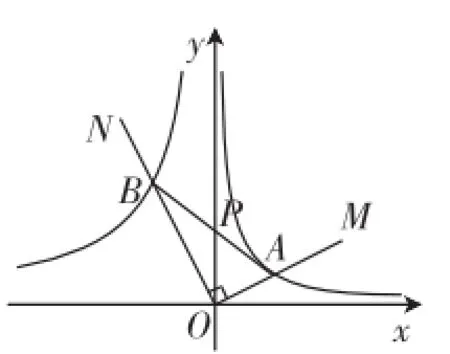
图5

打磨意见：与第1稿相比，试题从250字精减为130字，特别是题干叙述简洁、自然，带有一般性．把∠MON＝90°改为后两个问题中“小题干”中的条件“OM⊥ON”，并且把原来“求出tan∠OCD的值”改为“求证：tanα＝4tanβ”，追求了多样化的设问方式．然而第一问求一个变化的三角形的面积，这种设问方式也不够恰当，需要改进；第二问“小题干”中的“∠OAB＝α，∠OBA＝β”没有能在②中发挥价值；图4、图5呈现了两种特殊位置形式，对学生的暗示作用稍显太强；还有，不同问题之间条件的关联、呼应还不够紧密．于是形成第3稿．

第3稿：如图6，在平面直角坐标系xOy中，射线OM、ON与曲别相交于点A、B，连接AB交y轴于点P．

图6

（1）求证：当AB∥x轴时，△AOB的面积为定值.

（2）当OM⊥ON时，记∠OAB＝α，∠OBA＝β．

①求证：tanα＝4tanβ；

打磨意见：这一稿主要优化了第2稿中几个不足，而且只有一个图，使得问题呈现更加简洁.然而OM、ON这两条射线只是为了带来两个交点A、B，其他的价值并不是很大，克服这个不足，带来了根本的命题转向，问题立即简化成第4稿（考题）．

（1）求证：当AB∥Ox时，△OAB的面积为定值.

（2）若OA垂直于OB，

①求证：OB＝2OA；

②当线段AB的中点在y轴上时，求点A的坐标．

命题意图：删减了射线OM、ON的表述之后，就不用再给出图像辅助思考了，改为让学生自己构造图像分析，这样一道试题只剩下90个字符、没有图形.追求“好的题目”（见文1）的一个表征：简洁好懂、自然生长.（2）①删减了旁枝“正切函数”的干扰，削枝强干，回归对函数本质的考查.由于考生需要自己构思图像、变换图像分析，难度增加了，所以最后一问只求A点的坐标，这样也回避了初中阶段“课程课标”限制的求直线与曲线交点的方程组“超标”问题．

二、进一步思考

1.由博返约，追求简洁，凸显数学味道

从上面的命题过程能看出，我们经历了丰富的思考，比如想通过一道综合题把太多的数学知识或方法综合进来，正是这种追求“大、全、泛”的命题取向生成了第1稿那样的大容量综合题，在后续打磨和优化后，仅从字数上看，从250个字符到130个字符，再到90个字符，简洁的追求确实是这道试题不断得到优化的一种动力.再有，第1～3稿兼顾了射线、垂直、平行、锐角三角函数等几何元素，却使得试题成为“坐标系搭台，平面几何唱戏”的怪怪的试题（见文2），而第4稿则削枝强干，让问题回到函数主体，设问上也放弃了锐角三角函数，但求解时学生却可以思考相似、锐角三角函数等知识．

2．自然生长，内敛藏锋，追求教学导向

打磨到第3稿、第4稿时，基本追求了章建跃教授倡导的“好的题目”追求简洁好懂、自然生长的要求．值得一说的是，前面3稿的最后一问都需要分类讨论，为何第4稿却放弃了分类讨论？一方面是整卷上已有其他几处涉及分类讨论思想方法；另一方面，这种设问取舍也是基于一种“内敛藏锋”的命题取向，即命题者常常需要把对一个问题深入研究的探索成果经过取舍后设问，而不宜在试题上要求考生圆满解答命题者命制期间获得的太多结论．还有，除了追求试题的考查、区分功能，作为全卷的把关题，还需要认真构思试题的教学导向，像第4稿这样的试题，就导向重视函数概念的教学．

1.章建跃．发挥数学的内在力量，为学生谋取长期利益［J］．数学通报，2013（2）.

2.贺信淳．从多角度审视一道中考试题说开去——谈对初中数学教育现状之惑［J］．数学通报，2013（12）.Z