解题教学“慢一点”，“示错究错”做起来——以“二元一次方程组解决实际问题”为例

☉河北任丘华北石油机关中学 平同茹

解题教学“慢一点”，“示错究错”做起来
——以“二元一次方程组解决实际问题”为例

☉河北任丘华北石油机关中学 平同茹

近读专业刊物，关注到江苏省中学数学特级教师孙朝仁先生关于“慢教育”的系列文献，笔者受益颇多.作为一种实践跟进，最近有机会执教“二元一次方程组解决实际问题”的习题课，立足于“慢教育”的理念追求，笔者引领学生进行深度究错、有效用错、追求无错的数学体验.现将课堂中的几个重要教学片断梳理如下，并教后反思，供研讨.

一、教学片断及分析

课堂片断1：究错——这样做为什么不对

题目：（人教版七年级下第102页）用白铁皮做罐头盒，每张铁皮可制盒身25个，或制盒底40个，一个盒身与两个盒底配成一套罐头盒.现有36张白铁皮，用多少张制盒身，多少张制盒底？

（学生尝试进行独立思考，笔者通过巡视及关注弱势学生，收集典型错误或问题答案，并制成选项的形式，供学生进行究错）

设用x张铁皮做盒身，y张做盒底，可以使盒身与盒底正好配套.

师：请大家作为数学“医生”，诊断为什么这样做不对.

生1：A答案的方程（2），把x和y分别当成了盒身与盒底的个数.

师：一语道破！在列方程时，首先明确所设定的未知数的含义.

生2：B答案的方程（2），混淆了铁皮张数与盒身、盒底的个数的关系.

师：一针见血！那么铁皮张数与做成的盒身个数及盒底个数的关系是什么呢？

生3：盒身（底）个数=铁皮张数×每张铁皮能做的盒身（底）的个数

师：很好！也就是成品的总数量=原材料的总张数×每张原材料能做的成品个数.

生4：C答案的方程（2）中的25x和40y分别表示盒身的个数与盒底的个数，不能在题中找到它们的和，因此这样列不出来.

师：大家同意他的看法吗？

（大家异口同声表示同意）

生5：老师，我不同意，C答案的（2）能继续列出来，25x+40y表示所有的盒身与盒底的个数和，应该等于3× 25x.

（教师在学生5讲完后，画出来示意图）

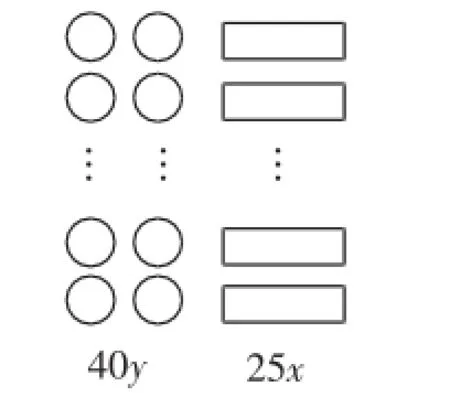
（学生恍然大悟）

生6：从老师画的示意图，可以看出来盒底是盒身的2倍，D答案中的方程（2）应该是2×25x=40y，这个答案弄错了倍数关系.

师：对于D中的错误，老师感觉有的同学不只是弄错倍数关系的问题，还有一种可能是审题时，根据两个盒底与一个盒身配一套这句话，（边讲边在题目中画出“两个”二字）就机械地在盒底前面乘以2，这种解题方式非常不可取，在分析问题时，一定要找到数量之间的关系.

课例片断解读：出示题目后，笔者没有按通常的模式由优秀生快而准地说出正确答案，而是注重课堂观察，呈现学生们的典型错误，将课堂生成资源作为本节课的切入点，同时也为全体同学搭建了一个良好的究错平台，通过此平台，那些顺利写出正确答案的同学不做冷眼旁观者，而是饶有兴致地走到题目深处去研究他人错误产生的原因，从多角度、多层面对题目进行剖析，借助他人的错误警醒自己.这种慢下来的驻足究因，不会使出错者出现假订正现象，而是引导出错者在理解了“我为什么这样做不对？”之后，自然而然地在个人的知识体系中对错误进行真订正.事实上，在课堂进行过程中，笔者注意到出错的同学不断地发出“噢！明白了”顿悟的声音，然后进行了自主订正，究错效果非常好.

课堂片断2：用错——你的错误，大家的财富

师：既然A、B、D三个答案都不是本题的正确答案，那么在保留这些答案的前提下，试着改改题目使这些答案成为正确的.

生7：我认为适合答案D的题目最好改，应该改成“用白铁皮做罐头盒，每张铁皮可制盒身40个，或制盒底25个，一个盒身与两个盒底配成一套罐头盒，现有36张白铁皮，用多少张制盒身，多少张制盒底？”

师：看来是个底大身小的盒子，非常好！

生8（抢答）：适合答案A的题目“用白铁皮做罐头盒，做盒底的铁皮是做盒身的铁皮的2倍，现有36张白铁皮，用多少张制盒身，多少张制盒底？”

生9：适合C的题目为“用白铁皮做罐头盒，每张铁皮可制盒身25个，或制盒底40个，现做成的盒底、盒身的总数为36个，且做盒底的铁皮是做盒身的铁皮的2倍，问：做成的盒底、盒身各多少个？”

师：以上同学都能紧紧抓住等式及各式的关系，正确地还原题目，说明能准确地理解各未知数及代数式的含义.这要感谢刚才出错的同学，正因为你们的错误，才让大家学到这么多，你们的错误，大家的财富！

课例片断解读：究错后，笔者没有就此停止，而是进一步借助错误资源，进行拨乱反正，要求学生为错误答案编出正确的题目.毫无疑问，此过程训练学生对数学符号语言和文字语言的相互转化能力，培养了数学基本素养.此过程中学生表现出了较高的积极性，优秀生的抛砖引玉，带动了中等生创新性思维的灵动，弱势生也没有出错的羞愧感，而是为自己的错误发挥了作用而自豪，这样为以后打开他们的心扉奠定了很好的心理基础.

课堂片断3：无错——给你力量，你一定不会错

问题改编：用白铁皮做罐头盒，每张铁皮可制盒身25个，或制盒底40个，一个盒身与两个盒底配成一套罐头盒，现有36张白铁皮，设做成的盒身x个，盒底y个，且正好配成套，可以列出哪些等量关系呢？

师：这个问题，我们采取特别的回答方式，由小组长推荐本组中做原题时出错的同学来回答，前提是要坚信这位同学一定能做出来！

（小组长们热情满满，纷纷推荐各组的弱势生，“老师，我相信我们组甲同学（暂时这样称呼）一定能做出来！”“老师，我相信我们组乙同学能做出来！”……被推荐的同学有的犹豫，有的跃跃欲试，最后选定了四名弱势生来完成）

师：不经老师任何引导能列出的，可以坐下试着在练习本上列出.

（生10坐下开始列方程）

教师第一步引导：x、y分别表示什么？题中有哪些等量关系？

（停顿片刻，生11坐下开始列方程.还有两位，仍然有些犹豫）

教师第二步引导：x、y分别表示盒身、盒底的个数，那么用来做盒身、盒底的铁皮张数如何表示呢？它们都满足什么关系呢？

（生12、13同时坐下开始列方程）

教师总结：这几位同学在小组的支持下，获得信心和力量，经过独立思考把题目准确地完成了，这说明你们很有潜力，同时也说明信任和支持是力量的源泉，大家以后要多多互相给出力量！

课例片断解读：在教学中笔者一直在思考这样的问题：（1）一节课后，学生的思维能力如何最大化地得到培养、提高？（2）作为完整的一节课，反馈和评价如何体现？（3）什么是真正的小组合作？仅仅是共同完成一件任务吗？基于以上思考，在这一环节，笔者将这些进行了有机结合，从直接设元变成间接设元（培养了发散思维），利用同伴间的鼓励和支持（发挥了小组合作作用），由引导弱势生巩固前面两个环节的成果进行提问式引导（挖掘了弱势生的学习潜能和信心），更重要的是笔者在此过程中尊重了学生个体的成长特点，真正体现了“慢教育”的涵义.

二、教后反思

1.向学生传递“出错不可怕”的思想认识

日本数学家米山国藏曾指出数学的一个特征就是“一步一步向上走”.学生在学习过程中，对一些新知识、新约定、新定理的理解出现偏差或错误是不可避免的，这时究错就是十分必要的一个教学环节.有效究错的关键是教师要帮助学生树立不怕错的意识.鼓励学生敢于暴露错误，这样才有机会变错误资源为有效资源，使错误成为学生共同成长的财富；其次，教师通过引导学生用错能进一步提升错误的价值，从而变废为宝，用错后，不但优秀生和中等生的认知和思维得到提高，弱势生也能深深地感到自己的错误的价值.这样，弱势生不逃避错误，中等生不无视错误，优秀生不鄙视错误，这样的课堂才会是真正和谐的课堂，这样的教学才是有效的教学，才是人人都能得到发展的教学.

2.从“简单纠错”到“深度究错”

一是接受“这样做对”的结果；二是理解“这样做为什么对”的原因；三是分析“那样做为什么不对”的成因.三个层次大致对应弱、中、优三类不同层次学生的学习习惯.前两个层次纠错是治标不治本的水平，是“假”纠错，“真”纠错是要厘清“为什么那样做不对”，称之为“究错”，只有这样，才能真正纠正错误认知和错误经验，否则只能是对错误暂时的掩盖，因此必须引导学生达到“究错”治本的第三层次水平，才能使学生的新、旧知识真正顺利对接.本节课中，笔者引领学生进行了第三层次的纠错，不但使学生清晰认识到这样做是错的，还进行了归因分析，即这样的错是怎样导致的，是题意理解有错，还是储备知识有错，还是思想方法不科学等.这种究错方式是最有效的学习方式，学生用这样的方式学习，人人都能在原有水平上得到提高.

1.邱广东.慢教育的“冷”思考［J］.中学数学（下），2014（1）.

2.钱卫江.做好错例点评强化正向引导——以一元一次方程的解法为例［J］.中学数学（下），2014（6）.Z