基于整体观的单元教学实践与思考——以“幂的运算”新授课为例

☉江苏省无锡市东北塘中学 顾燕萍

☉江苏省启东南苑中学 李卫星

基于整体观的单元教学实践与思考
——以“幂的运算”新授课为例

☉江苏省无锡市东北塘中学 顾燕萍

☉江苏省启东南苑中学 李卫星

文1概述了著名特级教师李庾南老师的“幂的运算性质”课例，让我们得以一睹专家教师对“幂的运算”教学内容的深刻理解．本着实践跟进的积极态度，笔者最近在一次教研活动中也执教了该课，本文整理教学设计，并教后反思，供研讨．

一、“幂的运算”教学设计

（一）教学目标

（1）演算、归纳并证明幂的运算性质（同底数幂的乘法、幂的乘方、积的乘方），在此过程中感受从特殊到一般的数学思想方法；

（2）应用幂的运算性质进行简单的运算，学会步步有据，表达运算背后的算理.

（二）重点、难点

重点：幂的运算性质的探究、证明与简单应用；

难点：幂的三种运算性质容易混淆，提醒学生注意辨别．

（三）教学流程

【数学现实】

题1：计算：（1）2x+3x；（2）3a2b-2a2b；（3）6a5-2a5．

题2：计算：（1）2x·3x；（2）3a2b·2a2b；（3）6a5·2a5．

设计意图：代数学习的一个重点是数式运算，从数到式，需要经历运算法则的归纳、法则的应用、运算律的简化运算这样的学习程序，然而整式的加减之后，学生并没有直接学习整式的乘除，这是什么原因呢？这就正好可以解释有些学生在计算上面的题2时会有困难或障碍的原因了．我们通过这两组计算题，启发学生对比、思考为什么整式的乘法还没有系统学习，为引入本课即将要学习的幂的运算性质提供了一组“数学现实”．

【性质教学】

问题：如何研究幂的运算性质呢？

预设：分三种可能的情况，比如同底数幂相乘、幂的乘方、积的乘方．可以安排学生讨论后交流、完善，梳理出三种情况，并依次探究不同类型的幂的运算性质．

1.探究同底数幂的运算性质

演算：25×22＝______；a3·a2＝______；5m·5n＝______.

归纳：am·an＝______（m、n为正整数）.

证明：略．

设计意图：从特例演算到归纳概括，再到一般意义上证明性质，让学生感受到同底数幂乘法的运算性质是如何来的，为什么正确．

例1（1）a2·a5；（2）x·x6；（3）（-2）2×（-2）3×（-2）4；（4）xm·x2m-1．

讲评预设：例1比较简单，可以安排班级中数学适应性不好的学生讲解他们的运算思路，追问他们每一步的算理，促进其他同学同步思考每一步的算理是什么.

例1的变式：（-2）2×（-23）×（-24）.

讲评预设：引导学生学会辨析这组运算的底数与前面的区别，让学生注意符号问题．

2.探究幂的乘方

演算：（32）3＝32×32×32＝36；（a2）3＝a2×a2×a2＝a6；（am）3＝am× am×am＝a3m；……

归纳：（am）n＝amn（m、n为正整数），即幂的乘方，底数不变，指数相乘．

证明：略．

设计意图：从特例演算到归纳概括，再从一般意义上证明性质，可以渐渐放开由学生参与，与“同底数幂的运算性质”的探究过程相比，这里更强调由学生给出一般意义上的证明，让学生感受到数学的严谨与理性．

例2（1）（103）4；（2）（a5）5；（3）（an）3；（4）-（a4）3．

讲评预设：这里4个例子都是直接使用幂的乘方运算性质计算，注意安排学生辨析（2）的运算与“a5·a5”之间的区别；（4）则需要引导学生看清底数与负号的关系．

例2的变式：计算-（a4）3·（-a4）3．

变式意图：进一步训练学生看清底数与负号的关系，同时又初步接触幂的运算的混合运算，还需要应用同底数幂的运算计算．教学时可以安排两名学生到黑板上板演，然后追问他们每一步的算理，以此强化算理意识．

3.探究积的乘法

演算：（ab）2＝（ab）·（ab）＝（a·a）·（b·b）＝a2b2；（ab）3＝（ab）·（ab）·（ab）＝（a·a·a）·（b·b·b）＝a3b3．

归纳：（ab）n＝anbn（n为正整数）.

证明：略，安排学生口述证明过程．

设计意图：演算安排学生讲述，归纳及证明也由学生口述，节约教学时间，这是因为通过前面两个幂的运算性质的总结思路学生已有相关经验，这里不必再耗费太多教学时间，重在后续法则应用．

例3（1）（2x）4；（2）（-5x）3；（3）（ab2）3；（4）（-2a2）5．

讲评预设：安排4个学生上台板演后，再安排另外4个学生评价前者的运算，并指出每一步的算理．

例3的变式：计算（ab2）3·（-2a2）5．

变式意图：其实是例3（3）、（4）两问的进一步相乘，增加了解题层次，使得问题一步一步向上走，成为一道幂的运算的混合计算题，也是后续将要学习的单项式的乘法．

【巩固训练】

题1：下列各式的运算结果为x6的是（）.

A．x9÷x3B．（x3）3C．x2·x3D．x3＋x3

题2：计算：m2·m3＝_________．

题3：计算：（-a2b2）2·a＝_________．

题4：计算：（1）（x2y）3=_________；

（2）（a2）4·（-a）3=_________.

【小结和作业】

引导学生回顾本课所归纳和证明出来的几种幂的运算性质，在具体应用时如何辨明类型、选准性质是计算的关键．布置作业，由教材改编设计两道题.

题目1：计算：

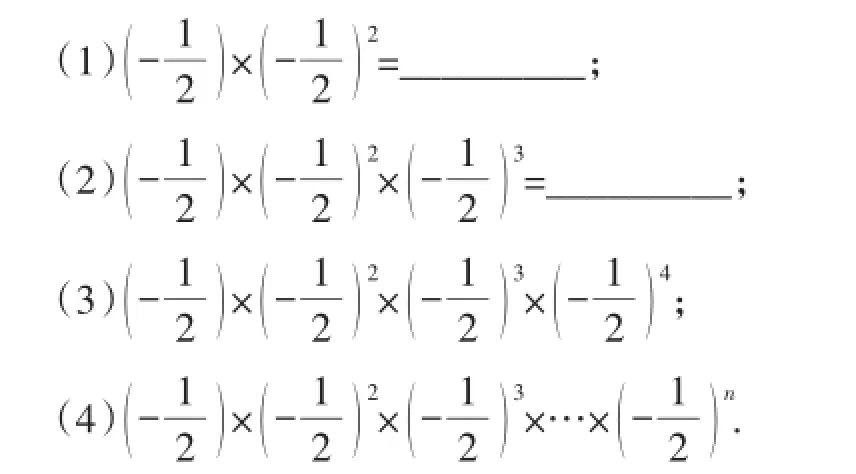
题2：计算：（1）（-2x）2＝________，（-3y）3＝________；（2）（-2a）3·9a2；（3）（-2b）3·（-3b）2；（4）练习上述题目后，你能积累怎样的计算经验？

二、教学立意的整体阐释

1.基于数学整体观，开展单元教学

受益于文1中的推介，笔者得以认真学习了李庾南老师对幂的运算性质的深刻理解，也反思了过去多少年都是按照教材上的顺序将同底数幂的乘法、幂的乘方、积的乘方分为三个课时开展教学，然后通过大量的习题训练来巩固．比较来看，基于数学整体观，实施幂的运算的单元教学显得更为合理，在后续教学时，再围绕幂的运算性质开展习题课，就可以避免本节课中训练量不够的问题．特别值得指出的是，在幂的运算性质单元教学的起始课中，需要十分重视法则发现、概括、证明，又要在例题应用时注意算理的掌握．

2.注重变式教学，在追问中将问题生长拓展

众所周知，中国数学教学中注意变式教学，然而变式教学如何开展，特别是例、习题教学时如何由例、习题出发，变式、生长、拓展，体现变式过程中自然而然是广大一线教师需要深入修炼的一项基本功，这涉及对教学内容、待变式的例题和习题的深刻理解．正如上文中我们在“小结和作业”环节设计题1，就是基于我们对幂的运算性质与七年级有理数一章所学的乘方之间的关联设计而成．此外，在例题变式环节，我们也注意了对部分例题进一步生长、拓展，又要注意这是单元教学的起始课，保持适度的变式，因为更加复杂的综合运算会在后续习题课中进行训练．

三、写在最后

客观上我们也看到，因为不同版本教材常常基于教学时间的限制，而将一些数学整体知识拆分成几个课时（标志是教材上常常用所谓的“练习”隔开），同时不少教辅资料上的课时划分也“尊重”了教材上的这种划分，使得不少初任教师也据此简单地理解教材，从而按此划分课时，将有些本可以整合后作为单元教学起始课的教学内容分隔开来，不能很好地向学生传递“数学是一个整体”这一认识，不能不说是一种遗憾．我们数学教师是专业技术人员，理应有自己的专业判断和专业行为，笔者也坚信，随着“课改一定要改课”理念的深入推进，会有更多的同行认同并践行整合教材内容后的“单元教学”模式．

1.汤志良．步步有据：推导幂的运算性质——李庾南老师“幂的运算性质”课例赏析［J］．中学数学（下），2015（5）.

2.刘东升．关联性：一个值得重视的研究领域［J］．中学数学（下），2013（12）.

3.李庾南．自学·议论·引导教学论［M］．北京：人民教育出版社，2013．

4.葛媛．基于“数学现实”，探索“未知领域”——李庾南老师“分式方程”课例赏析［J］．中学数学（下），2015（8）.Z