特征函数的梯度估计
2015-03-21李上达周振荣
李上达, 周振荣
(1.湖北中医药大学 信息工程学院, 武汉 430065;2.华中师范大学 数学与统计学学院, 武汉 430079)
特征函数的梯度估计
李上达1, 周振荣2*
(1.湖北中医药大学 信息工程学院, 武汉 430065;2.华中师范大学 数学与统计学学院, 武汉 430079)
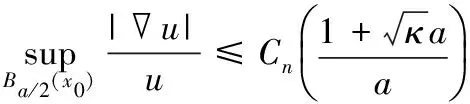
特征值; 特征函数; 梯度
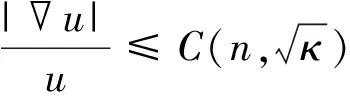
定理1如果M是n维黎曼流形,Ba(x)是M中以x为中心、以a为半径的球.对于充分小的a,如果在Ba(x0)上有Ric(M)≥-κ,κ≥0,Δu=-λu,u>0,则有
其中,x0∈M是任意一点.
1 定理的证明
证明分3步进行.
首先,运用Bochner 公式,有(Δu=-λu)
(1)
固定一点p,并在附近选取适当的标架,使得ui(p)=0(i≥2),u1(p)=(u)(p),所以有
故有
(2)
令
Δ|u|2=2|u|Δ|u|+2||u||2,
(3)
由(1)和(2)得
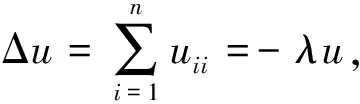
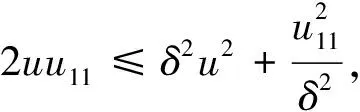
取δ2=mλ,其中,m>1,则
令m=n,则
于是有
(4)
直接计算得
(5)
Δ|u|=uΔφ+φΔu+2φu=
uΔφ-λφu+2φu,
由此得以及(4)得
对任意的ε>0,则由(6)得
(6)
代入(6)得
最后有
(7)
在Ba(x0)中考虑函数
其中,ρ是从x0算起的距离.注意F|∂Ba=0,如果u=/ 0,则F(x)必在Ba(x0)的内部达到极大值,并在极大值点上有u=/ 0.至于u≡0的情况,定理的结论自然成立.
设x1∈Ba(x0)为F(x)的极大值点.如果a充分小,则可使x1不是x0的割点,则由极大值原理有
F(x1)=0,
(8)
ΔF(x1)≤0.
(9)
在x1处,(8)为:
(10)
而(9)为:
(11)
将(10)代入(11)式得
(12)
(13)
其中,C是仅与n有关的常数.将上述估计代入(12)得
(14)
但在点x1处(10)成立,所以有
(15)
将(15)代入(14)得
(16)
把上式两端乘以(a2-ρ2)2,由于F=(a2-ρ2)φ,则在x1点有
其中,C1,C2是仅与n有关的常数,因此有
此时分两种情况计论:
(17)
因此当限制在Ba/2(x0)上时有
即
定理1得证.
2 推论
由定理1,很容易得到如下推论:
推论1如果M是n维黎曼流形,Ba(x)是M中以x为中心、以a为半径的球.如果在M上有Ric(M)≥-κ(κ≥0),Δu=-λu,u>0,则对于充分小的a有
其中,x0∈M是任意一点.
[1]ChoiHI,WangAN.Afirsteigenvalueestimateforhypersurfaces[J].JDiffGeom, 1983, 18: 559-562.
[2]KotaniM.Thefirsteigenvalueofhomogeneousminimalhypersurfacesinaunitsphere[J].TohokuMathJ, 1985, 37:523-532
[3] 丘成桐,孙理查.微分几何讲义[M].北京:高等教育出版社,2004.
An estimate of the gradients of some eigen-functions
LI Shangda1, ZHOU Zhenrong2
(1.Information Engineering College, Hubei University of Chinese Medicine, Wuhan 430065;2.School of Mathematics and Statistics, Central China Normal University, Wuhan 430079)
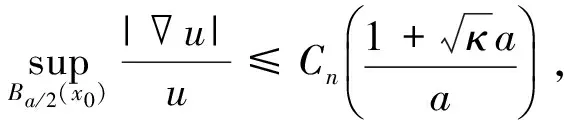
eigenvalue; eigenfunction; gradient
2014-08-29.
国家自然科学基金项目(10871149).
1000-1190(2015)02-0182-04
O186
A
*通讯联系人.E-mail:zrzhou@mail.ccnu.edu.cn.
