复合材料阻尼性能的测试与分析

武海鹏

(哈尔滨玻璃钢研究院，哈尔滨 150036)

复合材料阻尼性能的测试与分析

武海鹏

(哈尔滨玻璃钢研究院，哈尔滨 150036)

对复合材料的阻尼性能准确测试，实现对结构振动冲击、噪声和疲劳破坏的有效控制，有着极其重要的工程实际意义。本文从试验出发，通过Adams-Bacon法和Ni-Adams法对玻璃纤维和碳纤维复合材料单向板试件阻尼进行分析对比，讨论本文采用实验方法的可靠性。

阻尼；悬臂梁；纤维增强复合材料

1 引 言

先进的纤维增强复合材料由于高比强、高比模等优越性能，在航空航天、建筑、交通、机械等领域得到了愈来越广泛的应用。阻尼性能是先进复合材料应用中的重要组成部分，尤其在冲击、噪声领域中。在纤维增强复合材料阻尼性能分析及其预报方面，Schultz和Tsai[1]、Hashin[2]及Adams[3-5]进行复合材料阻尼开创性研究工作；其后德国的H.Oberst和法国的P.Lienard[6]对悬臂梁的结构损耗因子进行了理论分析和计算，其结构阻尼损耗因子可达到0.06～0.25左右；J.M.Berthelot和Y.Sefrani[6]对单向玻纤和芳纶纤维复合材料进行了研究，考察频率和纤维角度对复合材料损耗因子的影响。Adams&Bacon[4-5]以层合板阻尼性能实验结果为基础，提出了纤维增强复合材料阻尼元模型；Adams和Maheri[7]通过对不同铺设角度的层和板振动进行研究，得出铺设角度对于结构阻尼的耦合效应。Adams等[8-9]利用自由梁弯曲振动方法，研究了单向增强复合材料在不同温度下的动态特性和阻尼。冯文贤、陈新[10]等通过讨论振动系统的阻尼矩阵，构造了一个利用动态试验数据确定多项式的优化估计算法；丁康等[11]通过对自由衰减振动信号采集，利用离散频谱峰值，提出一种精确计算结构小阻尼的新方法；徐兴[12]等利用流变振动仪测设等截面杆的振动，来确定材料的阻尼，同样十分方便有效。 R.F.Gibson等[13]研究了短纤维增强复合材料中纤维相互作用、纤维长径比、界面结合状况等因素对材料阻尼性能的影响。

2 理论预测模型

预测正交各向复合材料梁的阻尼性能是由Adams et、Bacon[14]和Ni-Adams[15]开始研究的。Ni-Adams[15]通过考虑对称铺设复合材料梁的正应力σ1、正应变ε1、剪切应变γ1及其耦合的影响，对阻尼元的模型进行了修改，提高了预报的精度。主要考虑纤维角度和固有频率对于材料阻尼的影响。Adams和Maheri[7]同样使用了Adams-Bacon法对玻璃纤维和碳纤维层合板阻尼性能随着缠绕角度变化影响的研究。Yim-Jang[16]更多的使用了Adams-Bacon法研究各种类型的复合材料层合板面内剪切时的阻尼因子的情况。

2.1 Adams-Bacon法

对于正交各向异性材料的应力应变关系可表述为：

(1)

其中柔度系数：

(2)

材料的损耗因子ψ表达为：

(3)

其中δU：单元应变能存储可表达为：

δU=δU11+δU22+δU66

(4)

δ(ΔU)：单元应变能耗散表达为：

δ(ΔU)=δ(ΔU11)+δ(ΔU22)+δ(ΔU66)

(5)

单元在材料主轴方向的应力表达式：

σ1=σxxcos2θ

(6)

σ2=σxxsin2θ

(7)

σ6=-σxxsinθcosθ

(8)

所以：

(9)

(10)

与坐标轴成θ方向的能量损耗率即损耗因子ψx可表达为：

(11)

2.2Ni-Adams分析

取试件作悬臂梁，长度为a，宽度为b。自由端x方向上加载Mx的弯矩，且My=Mxy=0。根据经典层合理论，弯曲率为：

(12)

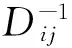
kx：沿x轴向的弯曲曲率；

ky：波松耦合曲率；

kxy：扭转弯曲耦合曲率。

对于悬臂梁结构，同样只σx考虑存在：

(13)

应力分量表达式为：

(14)

(15)

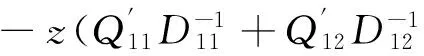
(16)

单元的耗散能量和总应变能表达式为：

ΔU=ΔU11+ΔU22+ΔU66

(17)

(18)

My和Mxy可忽略，则U的表达式：

(19)

则x坐标轴向的损耗因子：

ψ(θ) =ψx+ψy+ψxy

=ψ11a11(θ)+ψ22a22(θ)+ψ66a66(θ)

(20)

其中：

(21)

(22)

(23)

3 实验分析

复合材料阻尼性能与纤维角度、振动频率、树脂含量等多种因素有关，常用的测试方法有自由衰减法、相位法、振动法等。

3．1 自由衰减法

将所测试复合材料制成试样，测定试样底部响应衰减曲线，自由振动的振幅衰减速度和阻尼直接相关，用来衡量系统的阻尼特性。以自由振动时相继两次振动振幅比值的自然对数表示阻尼[17]：

(24)

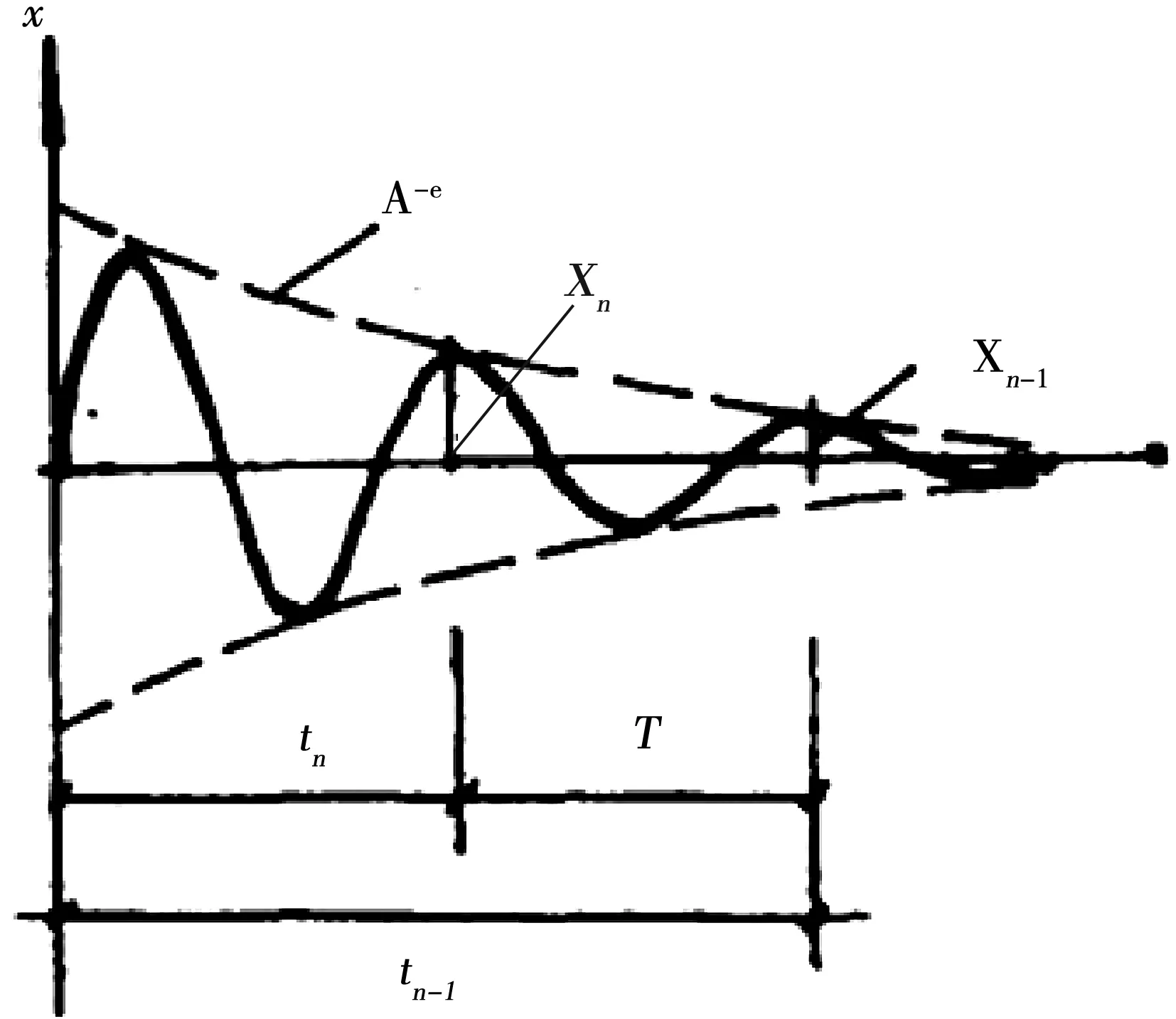
图1 自由衰减法振幅-时间典型曲线Fig.1 Free attenuation Curve

自由衰减法的测设系统主要包括试样端部装置[16]，激励信号系统和接受信号部分，由信号发生器通过电磁能转换器对试样施加激振力，然后由检测装置经信号放大器送入记录和分析仪器进行数据处理，计算阻尼因子。

3.2 相位法

通过测量频率而变化的相位差求的材料损耗因子的连续频率谱线。系统在运动每周振动所消耗的能量(ΔW)与其最大应变能(W)的比值，即耗能比(Ψ)表征阻尼大小：

(25)

粘弹性材料的阻尼，当其受到的外力与角频率为ω有关时，材料的应力应变会有滞后现象，即应力-应变曲线为椭圆形的滞回曲线。

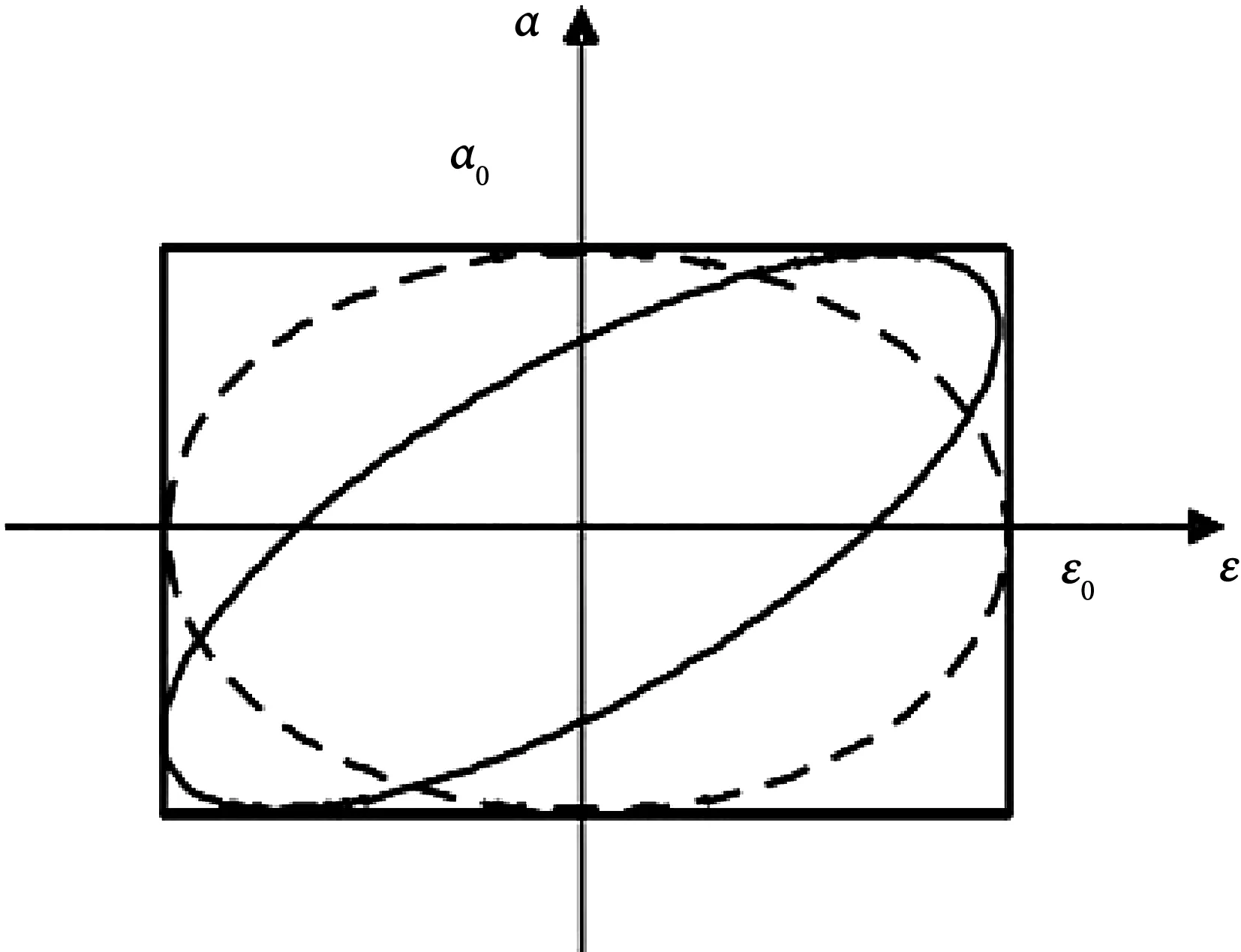
图2 相位法-滞回曲线Fig.2 Stagnant Curve

相位法主要采用扭摆仪测设各类材料的机械振动能吸收谱[17]。扭摆仪主要由试样、夹头和惯性体组成，试样的一端用工装固定，另一端通过工装和自由转动的惯性体相连。

3.3 振动法

将测试的复合材料制成梁，测定梁的振幅-频率曲线，可得到相应的结构损耗因子。

悬臂梁法测设阻尼因子的实验装置最初是由和Adams-Bacon与AdamsAdams[4-5]共同发展的。测试阻尼的悬臂梁振动频率一般在30-1 000Hz。在悬臂梁中间放传感器，通过电荷放大器将测力计所测数据传递给数据分析仪。这套装置与Gibsonetal[18]测试玻璃纤维/DX310树脂试件相同，所测实验结果阻尼的峰值出现在缠绕角30°左右。

本文试件参照中国国标GB/T18258-2000[19]，美国国标ASTME756-04[20]，采用振动法进行实验。实验装置如下：

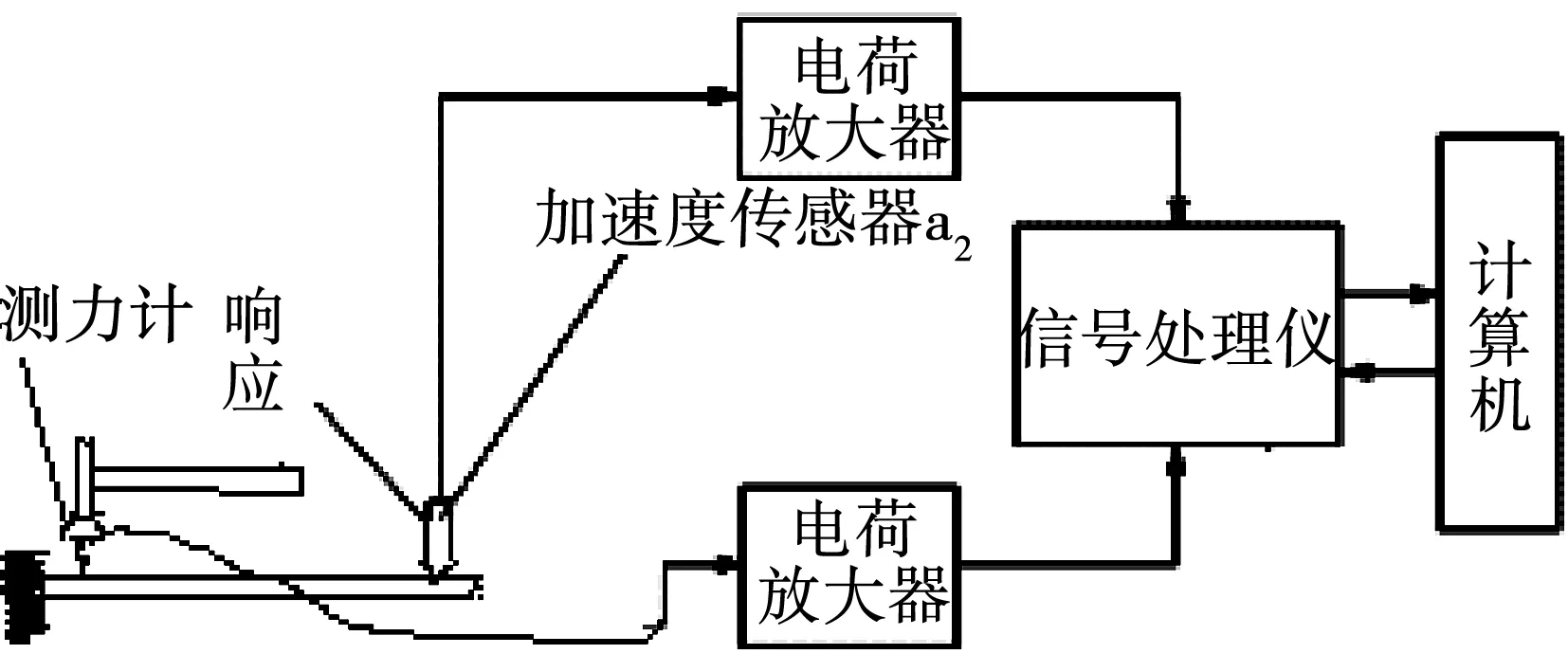
测试系统的仪器由激励部分和检测部分组成，对试样一端施加激振载荷。由检测传感器检测试样的振动响应信号，经信号放大器后送入显示与记录仪。输出信号计算得到频率-响应函数曲线。根据半功率带宽法计算阻尼比ζ，通过公式间接求出材料的结构阻尼(损耗因子η)。

试件为纤维单向角度，试件尺寸分为200×10×2 mm、180×10×2 mm，目的在于获取不同的频率对于阻尼结果的影响。试件纤维与主轴方向取7种角度：0°，15°，30°，45°，60°，75°，90°。

本次实验中使用的试件材料为玻璃纤维、碳纤维(T700)和环氧树脂，纤维体积分数60%。

4 阻尼与频率的关系

静力实验中测得玻璃纤维单向板工程常数：

EL=46 GPa,，ET=10 GPa，GLT=4.6 GPa，

ν=0.3

Q11=50.5 GPa，Q12=2.57 GPa，Q16=0

Q22=11 GPa，Q26=0，Q66=4.6 GPa

碳纤维单向板工程常数为：

EL=144 GPa,，ET=12 GPa，GLT=4 GPa，

ν=0.3

Q11=158.2 GPa，Q12=2.32 GPa，Q16=0

Q22=13.2 GPa，Q26=0，Q66=4 GPa

图3-图5为玻璃纤维复合材料的不同角度试件损耗因子与频率变化时的曲线关系。

从图3-图5可以看出，玻纤复合材料的损耗因子与测设频率变化相关，频率增，损耗因子反而减小。损耗因子的峰值是出现在f=50 Hz，θ=30°左右。从图3可以明显的得出，f=50 Hz在时比100 Hz和300 Hz时，损耗因子Ψ大些。从而可以得出，如果提高材料或结构的损耗因子，可以通过降低频率来实现。

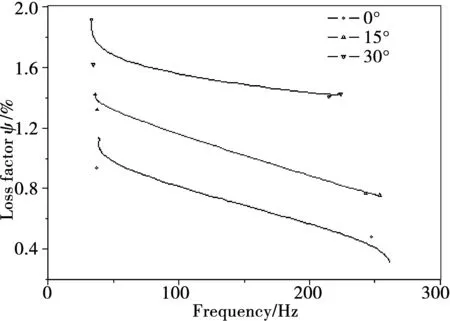
图3 玻璃纤维复合材料频率与损耗因子的实验结果Fig.3 Experimental results obtained for the damping as function of frequency for different fibre orientation of glass fibre composites

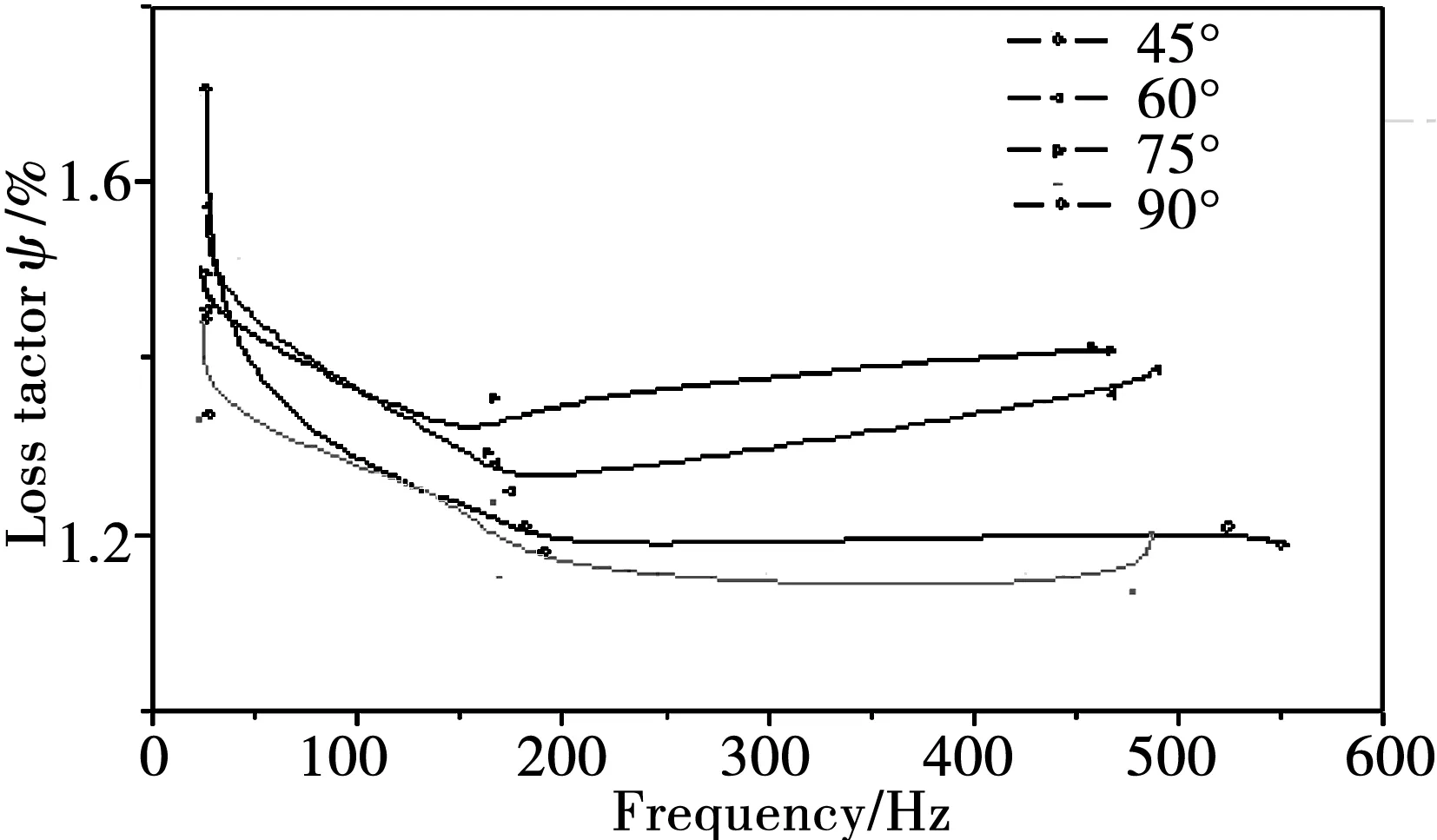
图4 玻璃纤维复合材料频率与损耗因子的实验结果Fig.4 Experimental results obtained for the damping as function of frequency for different fibre orientation of glass fibre composites

图6-图7所示为玻纤和碳纤维复合材料单向试件阻尼与Adams et-Bacon模型、Ni-Adams模型与实验结果的对比。从图中可以得出，复合材料的阻尼性能受到纤维角度影响比较明显。玻璃纤维数值结果ψ峰值出现在θ=35°时，ψ=2.09%，实验值为θ=30°时，ψ=2.236%；碳纤维数值结果ψ峰值出现在θ=35°时，ψ=1.78%，实验值为θ=30°时，ψ=1.77%。

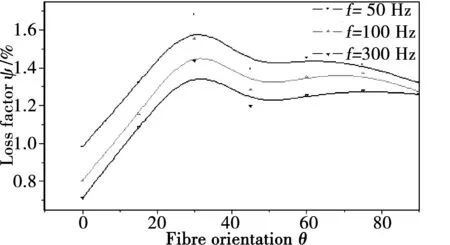
图5 玻璃纤维复合材料频率与纤维绕角度与损耗因子的关系Fig.5 Variation of damping as function fibre orientation,in the case of glass fibre composite

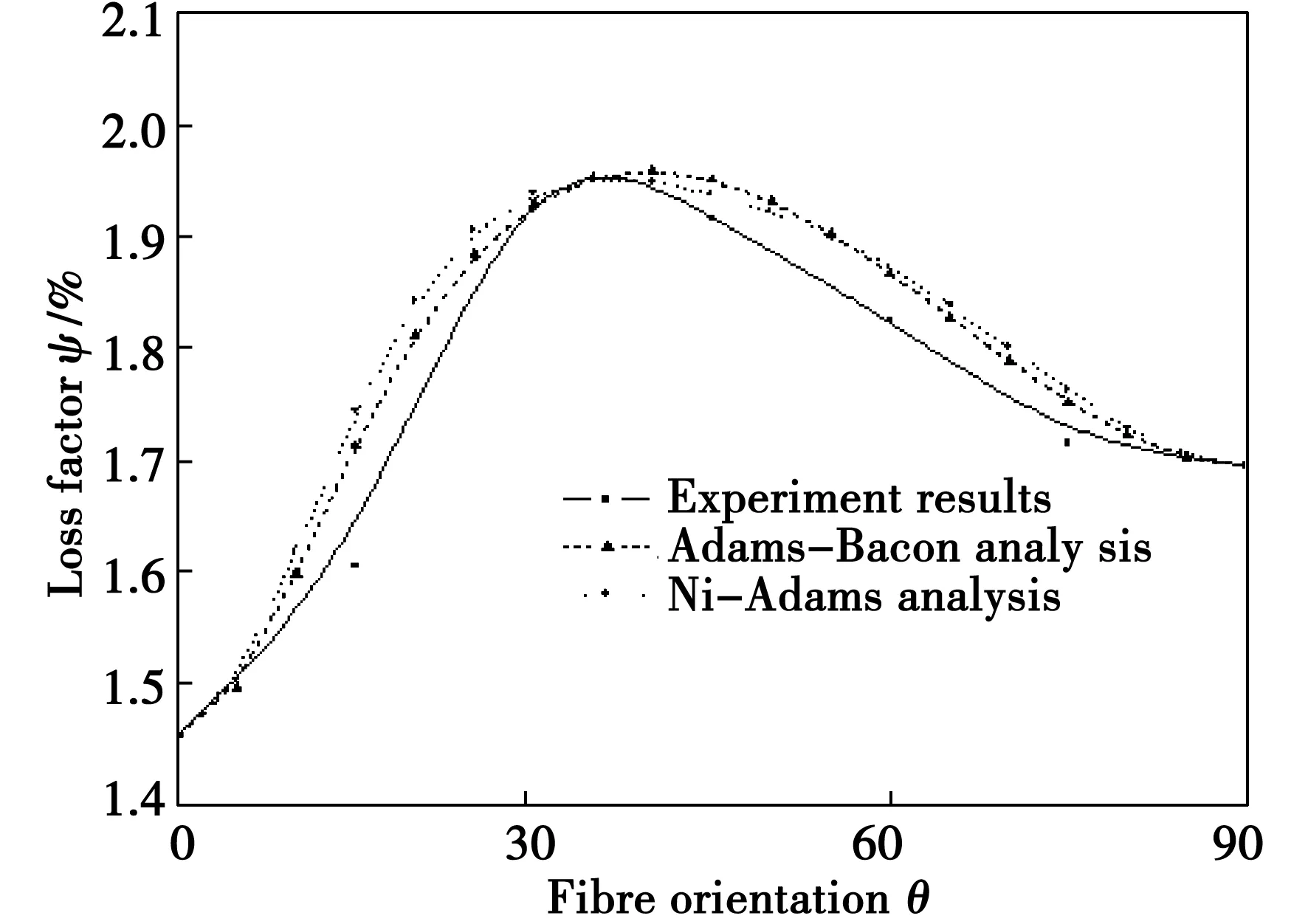
图6 玻璃纤维复合材料纤维角度与损耗因子的实验与数值结果对比Fig.6 Comparison between the experimental damping results and the numerical results,in the case of glass fibre composite

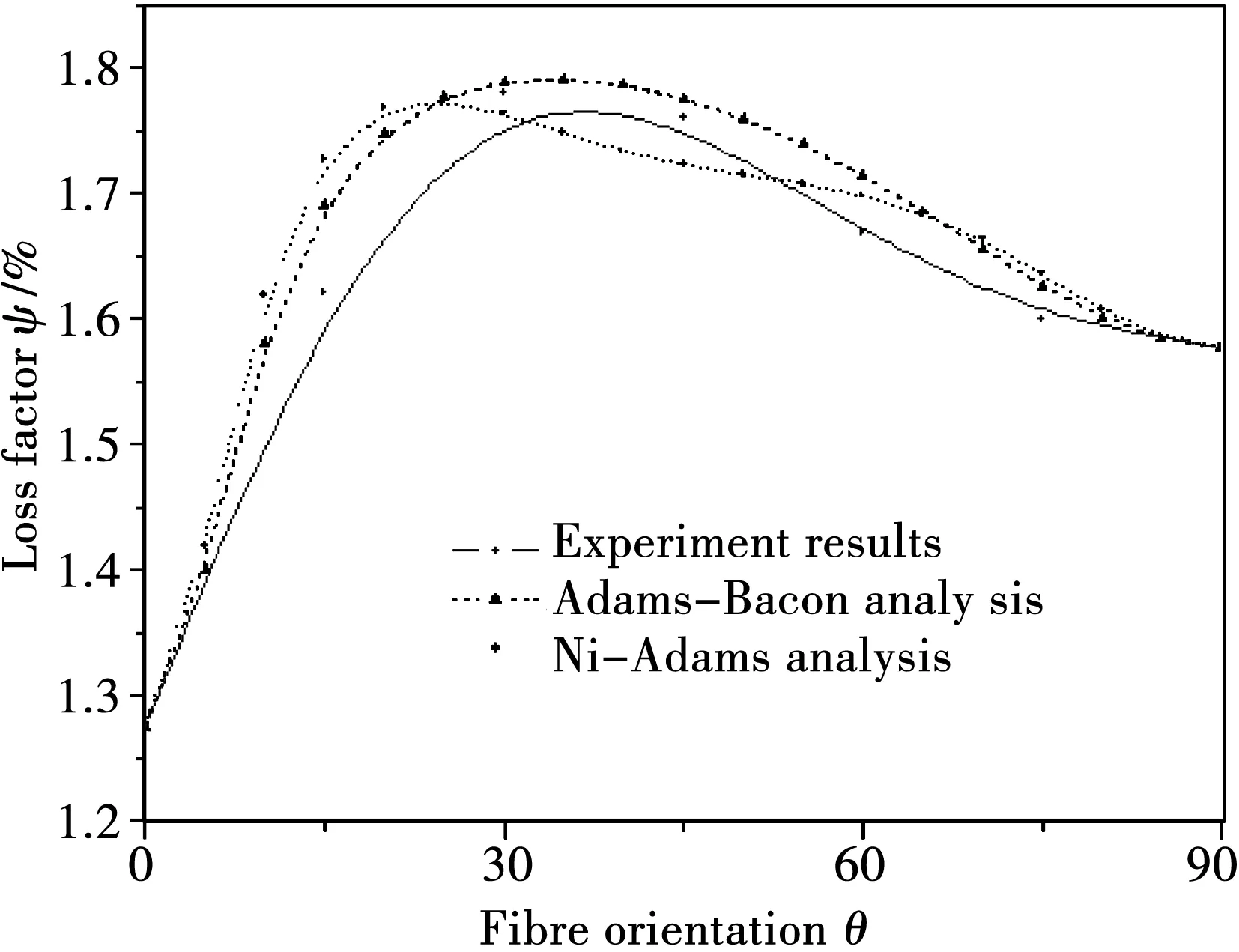
图7 碳纤维纤维角度与损耗因子的实验与数值结果对比Fig.7 Comparison between the experimental damping results and the numerical results,in the case of Carbon fibre composite

5 结 语

通过对玻纤和碳纤维复合材料试件损耗因子的两种预测结果与实验数据对比，可得出如下结论：

(1)复合材料的损耗因子有很多影响相关因素，比如纤维的角度θ、纤维体积分数、测试频率等。通过实验可以得出，降低测试频率有利于提高复合材料的阻尼性能；

(2)不同的复合材料损耗因子出现的峰值不同，这主要是由材料本身阻尼性能不同引起的。纤维体积分数相同时，玻纤比碳纤维复合材料阻尼性能更优越；

(3)本文所选用的振动法测试复合材料阻尼，与Adams et-Bacon法和Ni-Adams法2种理论预测结果符合，可以准确的得到复合材料材料单向板的阻尼性能。

[1] Schultz AB,Tsai SW.Dynamic moduli and damping ratio in fiber-reinforced composites[J].J Composite Materials,1968(2):368-379.

[2] Hashin Z.Complex moduli of viscoelastic composites General theory and application to particulate composites[J].Int J Solids and Struct,1970(6):539-552.

[3] Adams RD,Fox Mao,Flood.The dynamic properties of unidirectional carbon and glass fiber-reinforced plastics in torsion and flexure[J].J Comp Mater,1969(3):594-603.

[4] Adams RD,Bacon DGC.Measurement of flexural dynamic capacity and dynamic Young’s modulus of metals and reinforced plastic[J].J Phys D: Appl Plys,1973(6):27-41.

[5] Adams RD,Bacon DGC.Effect fiber-orinentation and laminate geometry on properties of CFRP[J].J Comp Mater,1973(7):402-428.

[6] Berthelot JM,Sefrani Y.Damping analysis of unidirectional glass and Kelvar fibre composites[J].Composites Science and Technology,2004,64(9):1261-1278.

[7] Adams RD,Masheri MR.Dynamic flexural properties of anisotropic fibrous composites beam[J].Comp Sci Technol,1994(50):497-514.

[8] Adams RD,Maheri MR.Damping in advanced polymer-matrix composites[J].Journal of Alloys Compounds,2003,355(1):126-130.

[9] Maheri MR,Adams RD.Modal vibration damping of anisotropic FRP laminates using the Ray-Ritz energy minimization scheme[J].Journal of sound and vibration ,2003,259(1):17-29.

[10] 冯文贤，陈新.结构振动系统阻尼矩阵的估计方法[J].广东工业大学学报，2006,18(3):57-60.

[11] 丁康，谢明，苏向荣.一种精确计算结构小阻尼的新方法[J].西安交通大学学报，2009,37(9): 17-20.

[12] 徐兴，凌道盛，吴强.阻尼材料复模量测设中的动力学分析[J].振动工程，1996，9(4):20-21.

[13] Gision RF.The use of strain energy-based finite element techniques in the analysis of various aspects of composite materials and structures[J].Journal of Composites Materials,1992,26(17):2585-2605.

[14] Adams RD,Bacon DGC.Effect of fiber orientation and laminate geometry on the dynamic properties of CFRP[J].J Comp Mater,1973(7):402-408.

[15] Ni RG,Adams RD.The damping and dynamic moduli of symmetric laminated composite beams theoretical and experimental results[J].Comp Sci Technol ,1984(18):104-121.

[16] Yim JH,Jang BZ.An analytical method for prediction of the damping in symmetric balanced laminates composites[J].Polym Comp,1990(20):192-199.

[17] Adams RD,Fox Mao,Flood RJL.The dynamic properties of unidirectional carbon and glass fiber reinforced plastics in torsion and flexure[J].J Comp Master,1969(3):594-603.

[18] Gibson RF,Yau A,Reigner DA.An improved forced -vibration technique for measurements of materials damping[J].Exp Techn,1982,6(2) :10-14.

[19] GB/T 18258-2000，阻尼材料-阻尼性能测试方法[S].2001.

[20] ASTM E756-04，Standard test method for measuring vibration-damping properties of materials [S].2005.

Damping Test and Analysis of Fibre Composites

WU Haipeng

(Harbin FRP Institute,Harbin 150036)

Damping is an important feature of engineering meaning.It’s behavior helpful control structure impact and yawp and fatigue.The experiment results compared with literature model: Adams-Bacon analysis and Ni-Adams analysis.Final,the paper discussed the dependability of experiments.

damping；cantilever；fibre reinforced composite

2014-10-19)

武海鹏(1977-)，男，河北人，硕士，工程师。研究方向：复合材料力学结构设计与工艺、有限元计算。E-mail：wu_effort@163.com.