短螺距手性液晶热敏旋光特性的研究
2015-03-21黄子强
李 君,黄子强
(电子科技大学 电子科学技术研究院,四川 成都610054)
1 引 言
手性液晶是指以螺旋方式排列的一类液晶,不同螺距的手性液晶分别具有旋光性、布拉格反射特性和光波导效应等光学特性。当入射光波长λ<n-p(n-为液晶的平均折射率,p 为螺距)时,光偏振面随着液晶分子的扭曲而转动,出射光矢量转过的角度与扭曲角相同,称为光波导作用;当λ=n-p 时,手性液晶液晶反射与其旋转方向相同的光,透射与其旋转方向相反的光,这一特性称为布拉格反射;短螺距手性液晶指λ>n-p 的手性液晶,入射光透过液晶相,其偏振面会转动一个角度,即旋光现象。旋光率的大小与手性液晶的螺距有关,其螺距受温度影响会发生规律性的变化[1],从而手性液晶的各项光学特性包括旋光率也将发生改变,通过测量手性液晶的光学特性变化可得到温度的改变情况,所以手性液晶可作为一种热敏材料应用于温度传感技术中。
国外已将热敏液晶测温技术大量应用于温度传感领域中,但国内这项技术还处于起步阶段[2]。1987年史永基提出了利用手性液晶来制作热色液晶温度传感器和数字液晶温度传感器[3]。热色温度传感器指利用手性液晶的布拉格反射,当螺距随温度变化时,反射不同颜色的光波,从而根据液晶的温度分布来检测物体表面的温度分布。2005年韩振兴建立了基于色调技术的热敏液晶定量测温系统,并把其应用于平板气膜冷却实验中,将热敏液晶所呈现色彩的色调与温度之间的关系用六次多项式进行拟合,使测量精度在95%置信区间内可达0.8℃[2]。数字温度传感器是利用测量短螺距手性液晶的旋光率来得到温度的变化情况,这种方法可以用来测量温度的微小变化,但其研究未给出旋光率的热敏规律。
为了得到旋光率随温度的具体变化情况,提供短螺距手性液晶热敏旋光特性应用于温度传感中的实验依据。本论文针对入射光波长远大于手性液晶螺距时,手性液晶旋光效应的理论计算,旋光率随螺距、盒厚、入射角等因素的变化特点及其热敏旋光特性进行了详细的阐述和研究。
2 原 理
2.1 手性液晶的旋光效应
手性液晶分子呈螺旋状排列,光沿螺旋轴通过手性液晶相时,不同螺距会有3种可能:光波导效应,布拉格反射效应和旋光效应。旋光效应是在入射光波长远大于手性液晶的光学螺距时,由于液晶分子的扭曲排列,使线偏振光的左旋和右旋分偏振光在液晶相中的传播速度不同而导致透射出来的合振动面发生了一定程度的转动[4],这样就可以使入射的线偏振光的偏振方向发生一定角度的偏转,这一偏转角度可通过旋光仪进行测量。
随着手性液晶的螺距、液晶盒盒厚和入射光角度等因素的变化,旋光的角度也会改变。由于手性液晶的螺距随温度变化较敏感,所以手性液晶的旋光率可随温度变化而发生变化。
2.2 4×4矩阵法
利用麦克斯韦方程旋转坐标系求解计算可以近似得到手性液晶的旋光角公式[5]为:
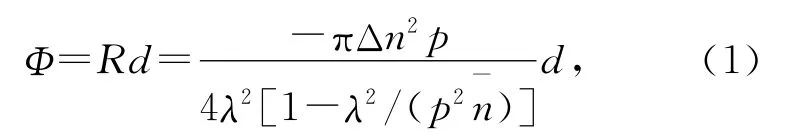
但这一公式只能得出旋光率的大致变化,与实际测量结果相差较大。Berremanrr 4×4矩阵方法利用麦克斯韦方程组进行计算,并考虑了多重反射,无论对于反射式还是透射式的液晶器件都可得到精确解[6-8],因此我们使用Berreman 4×4矩阵方法进行旋光率的计算。其原理如下所述。

图1 光线入射液晶薄层Fig.1 Light incident on the liquid crystal layer
将玻璃基板中间的液晶相分为很多如图1的薄层,入射光逐层入射。假设液晶层两边为各向同性介质,设光线与z 轴成θ0角斜入射,入射光场可表示为:
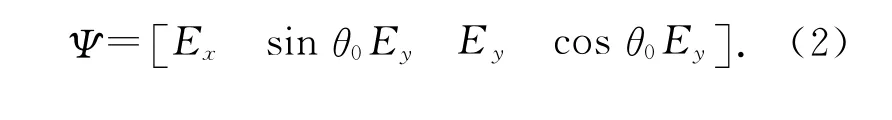
根据Berreman 4×4矩阵方法[8],麦克斯韦方程组可以用下式表示:

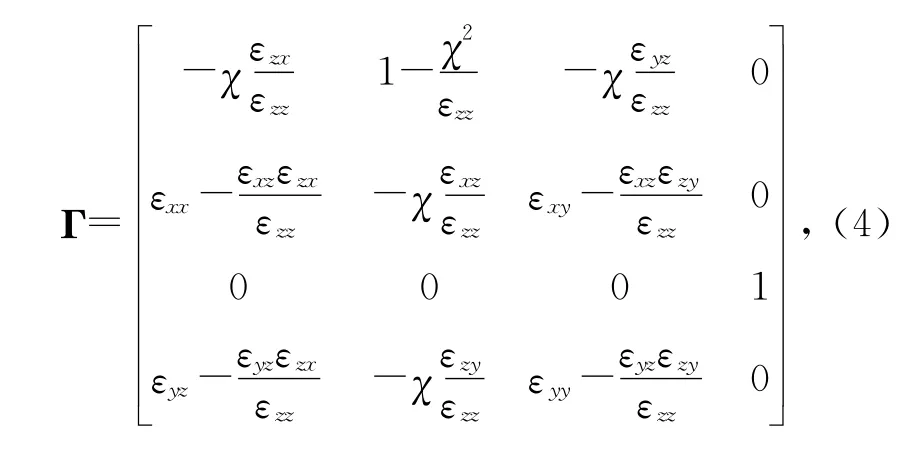
称为Berreman矩阵[9]。
ε为液晶的介电张量。将薄层视为均匀分布,每层厚度为Δz,每一层的介电张量随z 轴变化。介电张量随液晶指向矢的不同而改变,对于未加电场的手性液晶,以螺旋轴为z轴,介电张量ε()z 可由式(5)[9]计算得到:
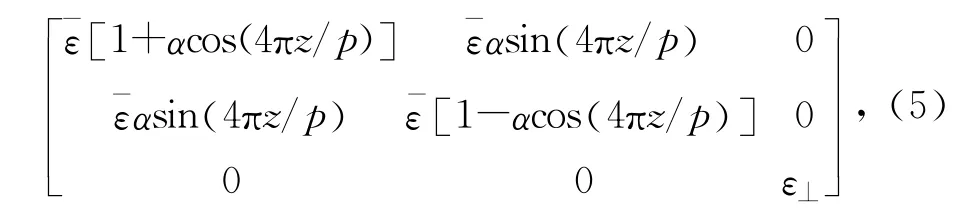
任意相邻的网格间Ψ 有近似解:
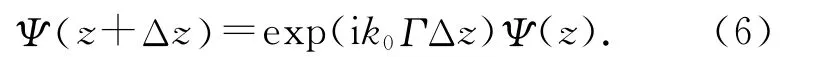
第i层的Qi=exp(i k0ΓΔz)值随z 的改变而不同,最终的透射光场可由式(6)决定:
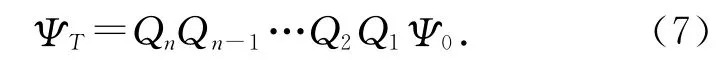
2.3 旋光的理论求解
根据4×4矩阵方法得到透射光场后,设透射光场为T=[TxTy]T,为计算旋光角度,可以通过比较光场透过检偏器后的光强寻找最大消光位置得到。
如图2所示,设作为检偏器的偏振片与x 轴的夹角为φ0。

图2 偏振片方向坐标Fig.2 Coordinate of polarizer’s orientation
根据马吕斯定律,可得此层琼斯矩阵如式(7)[10]:
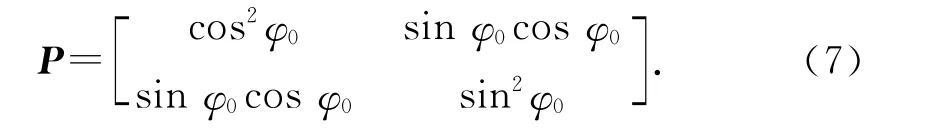
通过检偏器后的透射光场电场分量即为:

可得光强为下式:

使光强A 最小的φ0 就是最大消光位置,即可得到旋光角。例如入射光电场分量为[1,0],若当φ0=120°时A 最小,可得此时的旋光角为30°,如果是左旋手性液晶,旋光角则为-150°,即左旋150°。
3 实验与测量
3.1 实验方法
使用MATLAB 利用4×4矩阵方法改变入射角,螺距、盒厚等条件对手性液晶旋光率进行数值计算。不同螺距的手性液晶由手性剂CB15以不同比例与YM8型向列型液晶进行配比得到。CB15为右旋手性剂,其HTP值为7.9/μm。
3.2 测量系统
本论文使用上海光学仪器五厂生产的WXG-4型圆盘旋光仪进行实验测量。WXG-4 圆盘旋光仪,光源为中心波长589.3nm 的钠光灯,采用三分视界法来确定光学零位。
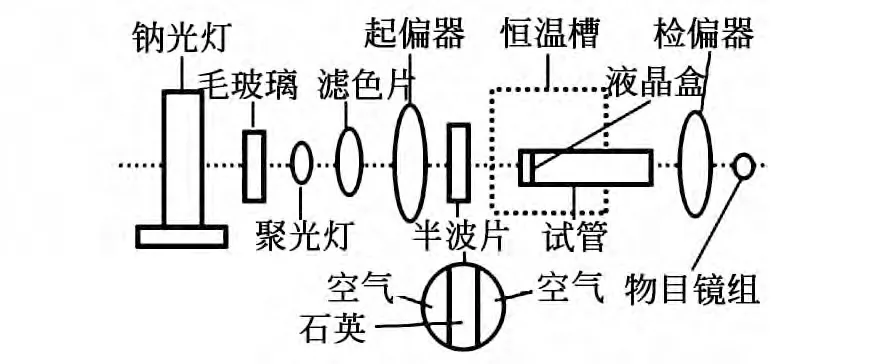
图3 WXG4型旋光仪光路图Fig.3 Measurement system of WXG-4polarimeter
旋光角测量光路如图3所示,恒温槽为测量时控制温度的附加器件。物目镜看到的视场被长方形石英片分为三视界,旋转检偏器会产生连续的亮暗变化,通过对比中间视场与两边视场的明暗程度来确定最大消光位置。当中间视场与两边视场一样暗时,即为最大消光位置,度盘上的读数即为此时的旋光角[11]。
4 结果与分析
4.1 不同条件下旋光率的计算及验证
使用旋光仪测得不同厚度旋光率随螺距变化的结果,与MATLAB 仿真结果进行比较。图4为垂直入射条件下,盒厚为6μm 和11μm 时旋光角随螺距变化的理论结果和实测结果比较曲线。图中实线为理论结果,实点为测量数据。

图4 盒厚6μm及11μm时旋光角随螺距的变化曲线Fig.4 Optical rotation angle versus pitch curve of 6μm and 11μm thickness
垂直入射时,250~310nm 螺距段的手性液晶旋光角随螺距及盒厚的增大而减小,验证结果与MATLAB的仿真结果相吻合。可以得出,随着螺距增加,这一波长下,的旋光率呈减小趋势。
斜入射时,如果使用中心波长进行计算,由于单一波长的高相干性对旋光有较大影响,得到的旋光率随入射角变化曲线会有大幅度的震荡,但实际使用的光源波长并不单一,曲线相对平滑的多,因此理论结果与实测结果出入很大。为避免这一问题,采用如下方法:由于钠黄光为589.0和589.6nm 的钠双线,分别计算589.0nm,589.6 nm 和中心波长589.3nm 时旋光角,使用这3种波长计算结果的平均值来近似实际情况,得到结果如图5中实线所示,图5为6μm 盒厚下螺距为290nm 时,斜入射条件下验证结果与理论曲线比较图。
结果显示,斜入射时,旋光率随入射角的增大而增大,这是因为当入射光角度不为零时,液晶分子对光矢量的旋转强度取决于液晶分子在与入射光法线垂直的平面上的投影,改变入射角相当于改变了手性液晶的螺距,所以入射角不同旋光率也会发生变化。随着入射角的增大,玻璃表面的衍射对旋光效应的影响越发明显,当入射角增大到60°左右时无法再观察到明显的旋光现象。

图5 斜入射时旋光角随入射角变化曲线Fig.5 Optical rotation angle versus incident angle curve of oblique incidence
4.2 旋光率热敏特性的实测结果
控制温度,进行不同温度下的旋光角测量。图6为盒厚6μm 时不同螺距下旋光角随温度变化的曲线。
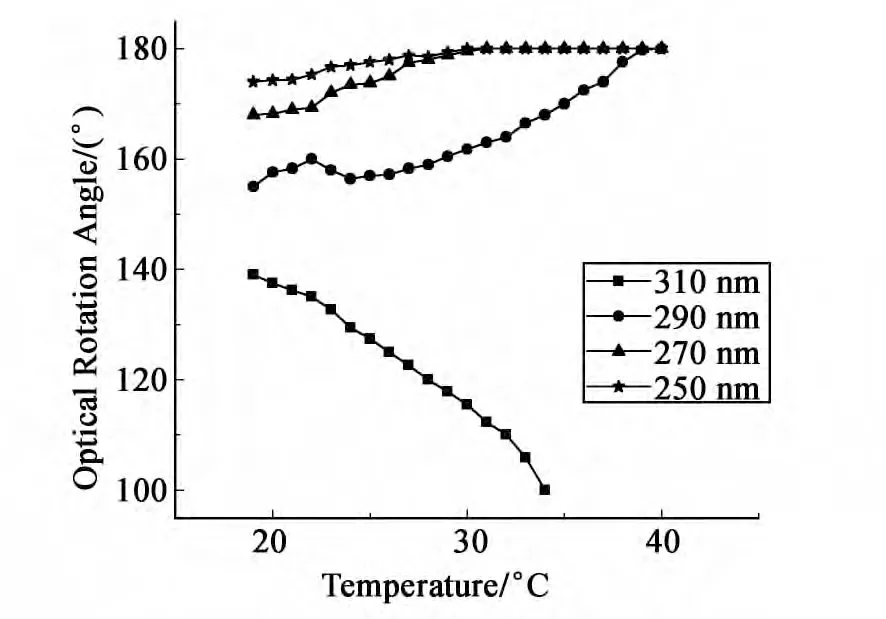
图6 旋光角随温度变化曲线Fig.6 Optical rotation angle versus temperature
螺距250~270nm 的手性液晶,旋光率随温度的升高而增大,直到旋光角增大为180°(测量时180°与0°为同一位置,所以实际是变为0°),由于温度升高使得螺距减小。由图4得到的规律可知,液晶分子入射光的旋光率逐渐变大,直到到达液晶清亮点[12],液晶变为各项同性的液体,这时液晶对光矢量没有旋光作用,出射光的偏振方向与入射光相同,因此测得的旋光率为零。
螺距为290nm 的液晶旋光率随温度升高总趋势为增大,但在某些温度下有波动,这是由于这一螺距段的液晶因为液晶盒取向,基板附近的液晶分子在加热到某一温度时指向矢发生180°的跳变,而不是连续变化导致。
螺距为310nm 的手性液晶,旋光率随温度的升高而减小,直至无法观察到最大消光,这是因为处于这一螺距的液晶在温度升高的过程中,螺距逐渐增大,当螺距足够大到超出旋光效应的螺距范围时,液晶对此波长的光不具有旋光效应,出射光不再是线偏振光,所以无法观察到旋光现象。
图6中,不同螺距的手性液晶旋光率随温度具有明显不同的变化趋势,这是因为由式(1)可以得出,手性液晶的旋光能力取决于螺距p,Δn 以及此时的入射波长λ,而对于不同螺距的液晶,温度变化可能引起螺距增大也可能减小[3]。如图6中所示螺距为250~290nm 的手性液晶,随温度的升高螺距p 减小,由公式(1)或Berreman4×4矩阵法可得此波长时,随着p 减小旋光率变大(如图4),这便导致了随温度的升高旋光率增大,相反螺距为310nm 的手性液晶随温度升高p 增大,所以呈现与其他螺距相异的热敏曲线。
不同厚度时旋光角随温度变化曲线如图7所示,螺距相同时,不同盒厚的液晶盒旋光率随温度变化的规律是相同的,因为温度只是是通过改变液晶螺距、双折射率等因素从而更改旋光率的,当入射光波长和液晶参数不变时,旋光率随温度的变化规律是一定的。

图7 不同厚度旋光角随温度变化曲线Fig.7 Optical rotation angle versus temperature of different thickness(6μm and 11μm)
结果表明,不同螺距的手性液晶旋光率随温度的变化规律不尽相同,这是因为对于不同螺距的液晶温度变化可能引起螺距增大也可能减小,且不同螺距段的螺距变化引起的旋光率改变方向不同。尽管不同螺距会呈现出不同热敏规律,但每种螺距下旋光角随温度的变化显著且有一定的规律。
4.3 热敏稳定性研究
上一节探究了手性液晶旋光率随温度的变化规律,然而若要将手性液晶的这一规律用于热敏材料中,则需要验证在各个温度下旋光角是否稳定在某个值的误差范围内。表1 为6μm 盒厚下,螺距为270nm 的手性液晶旋光率随温度变化的3次测量结果记录。
从表中可以看出,3 次实验结果相差较小,3组数据的方差仅为0.021°,波动很小,说明手性液晶的旋光率在温度不变的情况下基本稳定。

表1 手性液晶旋光率热敏稳定性Tab.1 Result of the stable study on optical rotatory of CLC (°)
5 结 论
本论文利用Berreman 4×4传输矩阵结合偏振光传播定律得到可准确计算手性液晶旋光率及其随外界因素(入射角,螺距,盒厚等)变化的方法,使用MATLAB 用此方法对手性液晶的旋光率进行建模与仿真,并通过测量CB15和YM8液晶配置得到的手性液晶多种条件下的旋光率对仿真结果进行了验证,实验结果表明,Berreman 4×4矩阵方法可以准确计算垂直入射和斜入射条件时的旋光角。结果表明在入射角大于一定角度时,不再具有明显的旋光效应。
通过对手性液晶热敏效应的实验研究,得出螺距为250 ~310nm 的手性液晶旋光率随温度变化情况虽不同,但旋光强度随温度都有明显且规律性的变化。论文同时验证了手性液晶旋光率的温度稳定性,得出对热敏特性的多次测量方差仅为0.021°,说明手性液晶温度不变时,旋光率稳定于某一数值,因此将手性液晶的旋光率可随温度规律性变化这一特性用于热敏材料中是可行的。
[1] 谢毓章.液晶物理学[M].北京:科学出版社,1998:568.Xie Y Z.The Physics of Liquid Crystals[M].Peking:Science Press,1998:568.(in Chinese)
[2] 韩振兴.热敏液晶测温技术及其在平板气膜冷却实验中的应用[D].北京:中国科学院研究生院,2005.Han Z X.Liquid crystal thermography and its application in flat plate film cooling experiments[D].Peking:University of Chinese Academy of Sciences,2005.(in Chinese).
[3] 史永基.液晶温度传感器[J].自动化仪表,1987(6):22-24.Shi Y J.Liquid crystal temperature sensor[J].Process Automation Instrumentation,1987(6):22-24.(in Chinese)
[4] 黄子强.液晶显示原理[M].北京:国防工业出版社,2008:98.Huang Z Q.Principle of Liquid Crystal Display [M].Peking:Nation Defense Industry Press,2008:98.(in Chinese)
[5] 刘厚通,李国华,郝殿中.螺状相液晶旋光特性理论模拟与实验研究[J].光学学报,2007,27(2):329-334.Liu H T,Li G H,Hao D Z.Theoretical simulation and experimental research of cholesteric liquid crystal optical rotatory characteristic[J].Acta Photonica Sinica,2007,27(2):329-334.(in Chinese)
[6] Hiap L O.Reducing the Berreman 4×4propagation matrix method for layered inhomogeneous anisotropic media to the Abeles 2×2matrix method for isotropic media[J].Journal of the Optical Society of America,1991,8(2):303-305.
[7] Wóhler H,Hass G,Fritsch M,et al.Faster 4×4matrix method for uniaxial inhomogeneous media[J].Journal of the Optical Society of America.A,1988,5(9):1554-1557.
[8] Berreman D W.Optics in stratified and anisotropic media:4×4-matrix formulation[J].Journal of the Optical Society of America,1972,62(4):502-510.
[9] WuJ W,Jisoo H,Ha N Y,et al.Nonlinear optical changes in 1-D photonic band gaps of cholesteric liquid crystal[C]//Photonic Band gap Materials and Devices,Proceedings of SPIE,2002,4655:303-308.
[10] 叶玉堂,饶建珍,肖峻,等.光学教程[M].北京:清华大学出版社,2005:346-348.Ye Y T,Rao J Z,Xiao J,et al.Optical Tutorial[M].Peking:Tsinghua University Press,2005:346-348.(in Chinese)
[11] 于晓红,连洁,龙爱群,等.WXG-4型旋光仪三分视场亮暗调节[J].物理实验,2010,30(3):32-24.Yu X H,Lian J,Long A Q,et al.Adjustment of bright vision and dark vision of WXG-4Polarimeter[J].Physics Experimentation,2010,30(3):32-24.(in Chinese)
[12] 杨磊,刘洋,郑永磊,等.胆甾相液晶盒贝纳德效应实验[J].液晶与显示,2012,27(3):288-291.Yang L,Liu Y,Zheng Y L,et al.Bernard effect experiment of cholesteric liquid crystal cel[J].Chinese Journal of Liquid Crystal and Display,2012,27(3):288-291.(in Chinese)
