基于Wu反走样的三角形光栅化边缘反走样算法

吴连慧，周建江，夏伟杰，陈雅雯

（南京航空航天大学 电子信息工程学院，江苏 南京210016）

1 引 言

在机载显示系统中，图形显示占据重要地位。传统的机载图形显示大多通过处理器（CPU）和软件方法实现。为了进一步提高图形的实时性，考虑到FPGA 具有强大的逻辑资源和丰富的IP核，利用FPGA 来代替CPU 完成图形处理的大量显示运算任务，实现图形硬件加速。

三角形光栅化［1－2］是图形光栅化模块中重要组成部分，许多复杂多边形的光栅化都可以在CPU 端分解为多个三角形光栅化命令，通过调用三角形光栅化模块来实现。由于三角形光栅化的边缘会出现明显锯齿现象，因此需要对其进行反走样处理。

本文基于水平线扫描转换设计了一种快速的三角形光栅化硬件加速算法。同时利用Wu直线反走样思想，研究三角形边缘反走样，提出了一种计算量小、显示效果良好的边缘反走样算法。并在FPGA 上实现了该算法。

2 三角形光栅化硬件加速算法

图形加速系统框图如图1所示，用户接口模块接收上层CPU 解析的图形命令，由图形光栅化模块来实现基本图元光栅化，并通过缓存管理模块将其存储到外部存储器中。

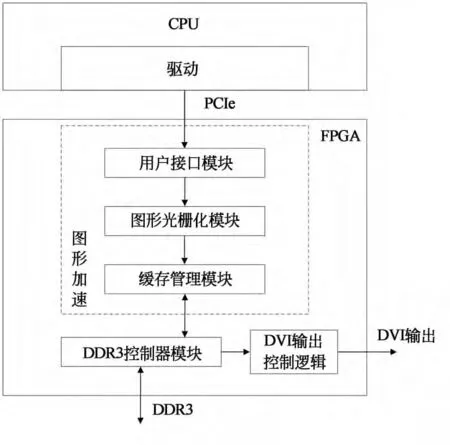
图1 图形加速系统框图Fig.1 Diagram of graphics acceleration

光栅化是指把物体的数学描述及其相关的颜色信息转换为屏幕上的像素的过程。三角形光栅化算法思想是，将三角形分解为水平直线顶点信息；再调用水平直线光栅化模块进行逐行扫描转换，从而实现光栅化。难点在于如何将三角形依次分解为水平直线端点。

三角形光栅化示意图如图2 所示。步骤如下：

图2 三角形光栅化示意图Fig.2 Schematic of triangle rasterization

（1）根据三角形顶点的纵坐标将3个顶点从小到 大 重 新 排 列，记 作（xmin，ymin），（xmid，ymid），（xmax，ymax），其中ymin≤ymid≤ymax，横坐标之间不存在大小关系。根据ymid所在水平直线将普通的三角形分解成上三角形和下三角形。同时计算出3条边的斜率：

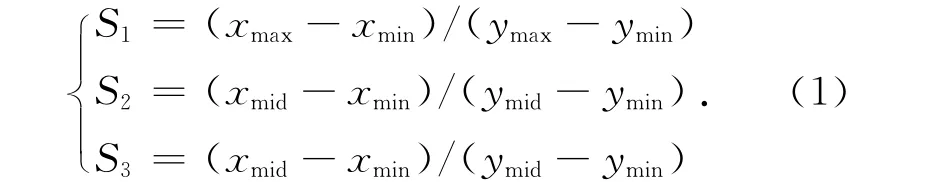
（2）对上三角形进行水平直线端点的分解，其中i是从1到（ymid－ymin）依次遍历的整数，则：

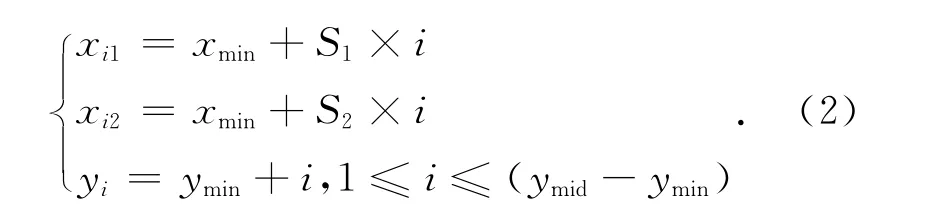
（3）对下三角形进行水平直线端点的分解，其中j是从0到（ymax－ymid－1）依次遍历的整数，则：

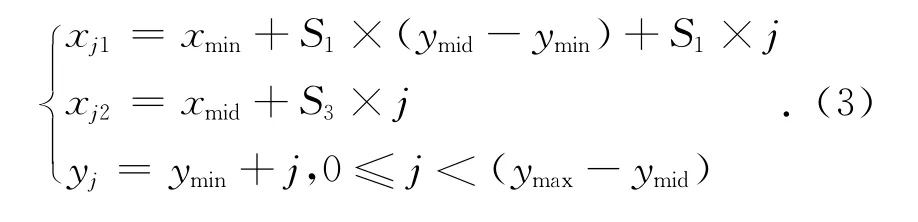
图3为三角形和四边形光栅化Matlab仿真图，可以看出，两者的边缘存在明显锯齿状的失真现象，所以需要进行反走样处理。

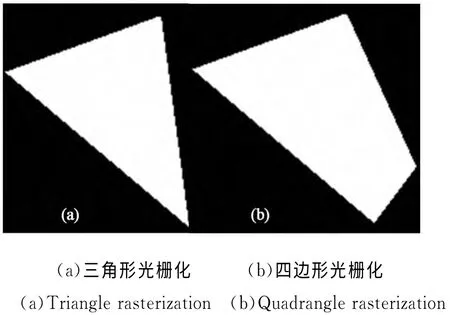
图3 光栅化仿真图Fig.3 Simulation of rasterization

3 基于Wu算法的边缘反走样

常见的三角形光栅化反走样算法有超级采样、多级采样和自适应采样等［3］，共同点是通过采样更多的子像素来反走样，在提高图形质量的同时，花费了较大的资源代价和时间消耗。考虑三角形内部像素点完全被三角形像素区域覆盖，不需要反走样，因此只需要对三角形边缘区域进行反走样，而三角形边缘是三条直线，因此考虑可以借鉴直线反走样算法对三角形边缘进行反走样处理。

3.1 Wu直线反走样算法

Wu直线反走样算法［4］是一种基于区域采样原理的简单有效且硬件易实现的直线反走样算法，其算法思想是：沿着长轴方向每前进一个像素单位，在短轴方向上距离理想直线距离最近的两个像素都点亮，两者亮度之和等于待绘制直线的亮度值，且距离理想直线远的亮度低，距离近的亮度高。Wu反走样算法原理如图4所示。

假设绘制颜色的亮度值为color，相邻像素坐标距离为1，若坐标（x，y）在从轴方向上与理想线段之间的距离为d（0≤d≤1），坐标（x，y）上像素点的亮度值表示为G（x，y），则：

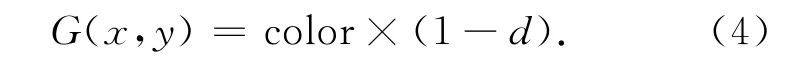
Wu反走样算法降低了直线光栅化时候的锯齿现象。借鉴这种算法思想对三角形边缘单独处理。

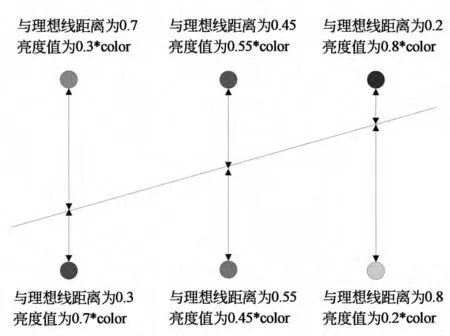
图4 Wu直线反走样算法示意图Fig.4 Schematic of Wu anti－aliasing algorithm

3.2 水平直线外侧直接添加插值点

由于三角形光栅化是基于水平直线扫描的，考虑每次生成水平直线时，直接利用Wu反走样的思想对水平直线端点进行反走样处理。

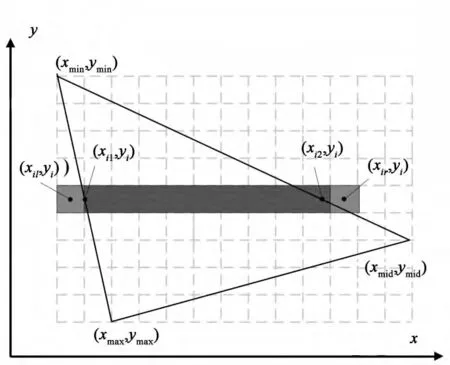
图5 水平直线外侧添加插值点示意图Fig.5 Schematic of adding interpolation points outer the horizontal line

图5为水平直线外侧直接添加插值点示意图。图中以上三角形水平直线外侧添加插值点为例，水平直线左侧的插值点坐标为（xil，yi），对应的像素点的亮度值表示为G（xil，yi），且插值点坐标（xil，yi）到 浮 点 坐 标（xi1，yi）的 距 离 表 示 为dli。则：

其中，? 表示向下取整。水平直线右侧的插值点坐标为（xir，yi），对应的像素点的亮度值表示为G（xir，yi），且 插 值 点 坐 标（xir，yi）到 浮 点 坐 标（xi2，yi）的距离表示为dri。则：

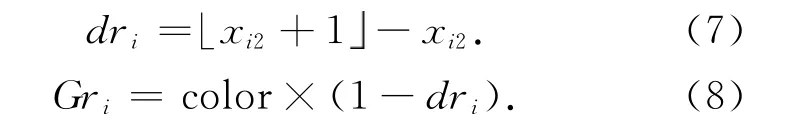
图6为三角形和四边形光栅化时水平直线外侧添加插值点仿真图。从图中可以看出当斜率k较大（｜k｜＞1／2）时，图形边缘反走样效果较好；但图形边缘斜率k较小（｜k｜≤1／2）时，反走样效果不好；且用三角形拼接成多边形填充时，拼接处会有虚化现象。不同斜率显示效果有差异的原因是，Wu算法是分长轴短轴的，按照长轴遍历和按照短轴遍历，效果是不一样的。而三角形分解成的水平直线是统一在水平直线端点两侧添加插值点的，本身不好区分长短轴，因此会影响反走样效果。三角形拼接处出现虚化现象是因为拼接处没有判断出是多边形内部的值，反而按照三角形边缘进行了插值处理，既浪费了时间又影响显示效果。

图6 水平直线外侧添加插值点仿真图 Fig.6 Simulation of adding interpolation points outer the horizontal

水平直线外侧直接添加插值点的方法比较简单，但缺点是，没有考虑长短轴的问题，当斜率较小时，效果不好；且拼接成多边形时，拼接处会有虚化现象。

3.3 三角形三边外侧反走样

水平直线外侧添加插值点的方法是对每次分解的水平直线端点进行处理，而不是将三角形3条边缘看作3条直线单独处理。考虑直接将其当作3条直线用Wu算法对直线进行单侧的反走样处理。图7为不反走样、水平直线外侧添加插值点、三边外侧反走样对比仿真图。从图中可以看出，当直线与水平线夹角在±30°之内时，该直线外侧反走样插值效果比水平直线外侧直接添加插值点效果好；其他情况下两者的效果相同。

图7 反走样前后仿真对比图Fig.7 Comparison of anti－aliasing effect

最终显示效果与图8右侧所示效果相同，三角形三边外侧反走样优点是显示质量好。缺点是，对于3条边本身来说，已经脱离了三角形的关系，很难判断哪边是外侧；对于同一条边，不同的三角形内外侧也不尽相同；对于同一条边，端点的顺序不同，内外侧是相反的。因此，对三角形三条边单独进行单侧反走样判断情况过于复杂。

4 改进的边缘反走样算法

分析上述两种方法的优缺点如表1所示。综合两者的优点，提出一种算法能够有较好的显示效果，同时实现简单且没有虚化现象。

表1 边缘反走样算法优缺点对比Tab.1 Advantages and disadvantages of different edge anti－aliasing algorithms

4.1 算法思想

4.1.1 边缘叠加Wu反走样直线

由于三角形三边外侧反走样效果好，但对于边缘直线本身，内外侧的判断比较复杂，所以考虑直接在三角形光栅化的基础上进行3条边的反走样绘制。直线和三角形命令都是由上层CPU 发送的，但底层FPGA 并行处理时，先后顺序是不定的。如果先绘制三角形填充再绘制直线，效果如图8（a）所示；如果先绘制直线，再绘制三角形填充，效果如图8（b）所示。从图8（b）看出，此方法效果比水平直线添加插值的方法好，与三边外侧反走样效果相同，但不需要进行内外侧的判断。考虑如何解决叠加顺序不定带来的影响。

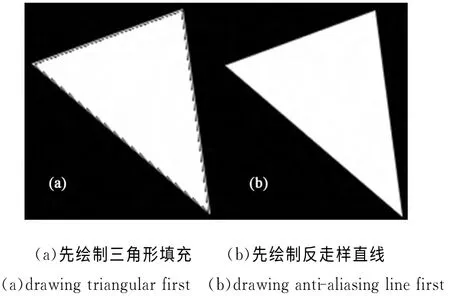
图8 边缘叠加Wu反走样直线仿真图Fig.8 Simulation of overlaying Wu anti－aliasing line for the edge

4.1.2 插值考虑背景值

为了解决叠加顺序不同带来的显示效果差异，在用单线宽直线反走样对边缘处理时，考虑当前坐标的背景颜色值对插值后颜色值的影响。假设坐标（x，y）在从轴方向上与理想线段之间的距离为d（0≤d≤1），坐标的背景颜色亮度为GB（x，y），当前图形颜色值为G，若坐标（x，y）上像素点的亮度值表示为G（x，y），则：

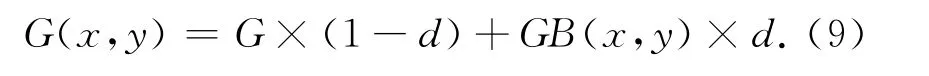
先绘制直线，再绘制三角形填充时，在两者重叠的坐标处，将三角形填充颜色值color直接写入到当前坐标对应的DDR3地址中，覆盖掉之前的插值结果。最终显示效果与图8（b）相同。

先绘制三角形填充，再绘制直线时，在两者重叠的坐标处，将背景值color从DDR3 对应地址中读回，代入公式进行计算，则

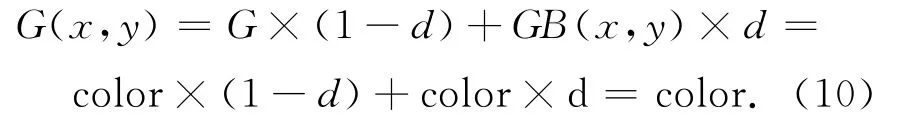
从公式可以看出，对于颜色值为color时，重叠部分读回背景值也是color，最终结果还是color，不会出现虚化现象。最终显示效果也与图8（b）相同。

当前方法效果好，简单易行，且不反走样三角形和反走样边界直线的顺序是任意的。多边形光栅化时，只需要发送多边形的边缘直线进行反走样，而不需要将分解的三角形各边都进行反走样。

此外，由于三角形光栅化是图形加速模块的子模块，图形加速模块也包括基本的反走样直线，可以调用现有的反走样直线算法，不需要另外编写程序。

4.2 FPGA仿真和硬件实现

在Xilinx的Kintex－7FPGA 上对不反走样三角形填充和边缘反走样进行ModelSim 仿真［5］和FPGA 硬件实现，对比边缘反走样前后的三角形光栅化效果。

4.2.1 ModelSim 仿真

三角形填充仿真时，令输入坐标为（280，100）；（300，250）；（170，140），对应的Matlab仿真效果如图3（a）所示。每解析出一条水平直线端点信息，就调用水平直线光栅化程序绘制出来。从图9可以看出，绘制时，水平直线的长度由短到长，后又由长到短。本文系统输出分辨率为1 920×1 080，帧速率为60 Hz，时钟频率为400 MHz。用新算法绘制该三角形光栅化时，耗时约33.75μs。三条边反走样绘制，耗时约2.16μs。相对于三角形光栅化消耗的时间，反走样处理占用时间少，且效果改进明显。

图9 三角形光栅化ModelSim 仿真图Fig.9 Simulation of triangle rasterization by ModelSim

图10 三角形光栅化及其反走样屏幕显示对比图Fig.10 Display comparison of triangle rasterization and its anti－aliasing

4.2.2 FPGA 硬件实现

新算法由于计算量小，适合于硬件实现。三角形光栅化及其反走样显示效果如图10 所示。可以看到反走样后显示效果比不反走样效果好。且用新算法绘制耗时远低于一帧图像的最大处理时间（16.7ms），满足系统设计要求，故可以用于机载图形显示系统。

5 结 论

介绍了三角形光栅化硬件加速算法，由于其边缘存在明显锯齿状的失真现象，所以需要进行反走样处理。基于Wu反走样算法的思想，考虑了水平线外侧加插值点和三边外侧反走样直线的算法。综合两者的优缺点，提出了一种改进的边缘反走样算法。该算法在绘制光栅化的三角形的同时，叠加考虑背景像素作用的Wu反走样直线。且用于多边形光栅化时只需要发送多边形的边缘直线进行反走样而不需要将分解的三角形各边都进行反走样。后续研究中可以进一步改进反走样直线的算法［6－7］，从而改进三角形反走样的效果。

经过对比，本文提出的三角形光栅化的边缘反走样算法有效提高了三角形光栅化后边缘的显示效果，计算量小、效果好，且易于FPGA等硬件实现。

［1］ 黄锐，付宇卓，赵峰.基于FPGA 的三角形光栅化模块［J］.计算机工程，2008，34（22）：242－244.Huang R，Fu Y Z，Zhao F.FPGA－based triangle rasterization module［J］.Computer Engineering，2008，34（22）：242－244.（in Chinese）

［2］ 饶志恒.图形处理器图形管线的研究与实现［D］.长沙：湖南大学，2011.Rao Z H.Research and implementation on graphics pipeline of graphic processing unit［D］.Changsha：Hunan University，2011.（in Chinese）

［3］ 黄锐.实时嵌入式图形系统中的三角形光栅化研究与设计［D］.上海：上海交通大学，2008.Huang R.Study and design of triangle raster in real－time embedded graphics system［D］.Shanghai：Shanghai Jiaotong University，2008.（in Chinese）

［4］ Wu X.An efficient anti aliasing technique［J］.Computer Graphics，1991，25（4）：143－152.

［5］ 王文华，何斌，任建岳.线阵CCD 成像系统自校图形设计［J］.光学精密工程，2009，17（8）：2011－2016.Wang W H，He B，Ren J Y.Design of self－check figures in linear CCD imaging system［J］.Optics and Precision Engineering，2009，17（8）：2011－2016.（in Chinese）

［6］ Xian Z，Xiaobing L.Improved DDA line drawing anti－aliasing algorithm based on embedded graphics system［C］.2010 3rd International Conference on Advanced Computer Theory and Engineering （ICACTE），IEEE，2010，2：V2－497－V2－499.

［7］ Yong J，Lu－ya W，Yue－yue C.The research and implementation of line anti－aliasing algorithm based on coordinate system rotation［C］.2010 International Conference on Audio Language and Image Processing（ICALIP），IEEE，2010：180－184.