拼接式编码器测角误差分析及试验
2015-03-21马文礼黄金龙
黄 龙,潘 年,马文礼,黄金龙
(1.中国科学院 光电技术研究所,四川 成都 610209;
2.中国科学院大学,北京 100049)
拼接式编码器测角误差分析及试验
黄龙1,2,潘年1,2,马文礼1*,黄金龙1
(1.中国科学院 光电技术研究所,四川 成都 610209;
2.中国科学院大学,北京 100049)
摘要:根据望远镜测角系统的精度需求,分析了影响拼接式编码器测角精度的误差源,以及多读数头测角消差原理,确定了采用相位相差90°的4读数头的测角方式。在某望远镜方位轴系转台进行了逆时针和顺时针方向的测角试验,通过对测角数据进行谐波分析并补偿后,得到两组实验测角误差RMS分别为0.34″、0.38″。实验表明,相位相差90°的均布4读数头的测角方式消除了由轴系误差、编码器安装位置误差和钢带安装盘部分圆度误差对测角精度的影响,实现了亚角秒级测角的目的。研究结果可用于大口径望远镜设计阶段的误差分析与分配、预估测角精度,为降低设计和加工误差提供参考。
关键词:拼接式编码器;测角精度;谐波分析;望远镜
Error analysis and experimentation of scale tape encoder
1引言
光电编码器具有高分辨率、系统精度、重复性能好、动态响应快、环境适应性强等优点,广泛应用于高精度测量角度的仪器设备中。光电编码器作为角度测量元件,主要应用在望远镜上,其测量精度直接影响望远镜的指向和跟踪精度[1]。现代光电望远镜的轴系尺寸较大,使得传统的玻璃圆光栅编码器不再适用,拼接式钢带光栅编码器由于具有精度高、装调简单、能灵活调整自身尺寸等优点,作为新一代测角编码器被广泛应用于现代大型望远镜测角系统中。近年来,随着测控技术的迅速发展,对光电轴角编码器的测角精度、分辨力和可靠性提出了更高的要求。光电编码器误差主要包括码盘制造误差、轴系晃动误差、码盘偏心误差、细分误差、量化误差、检测误差等[2-4]。这些误差来自于编码器的码盘刻划、机械装调、电子学处理等过程,其结果都会对编码器的测量精度产生影响。因此,对编码器的精度分析和误差补偿技术的研究有助于提高编码器精度[5-7]。
然而,编码器的测角性能常常会受到各种机械装调误差、零部件加工误差、测量过程随机误差等各类误差因素的影响[8],在系统测角精度要求为角秒或亚角秒级情况下,往往不能满足要求。为了减小编码器测角误差,需要研究其误差的来源,有针对性地控制误差源,提高系统的精度。国外很多望远镜项目如Very Large Telescope(VLT)、Large Binocular Telescope(LBT)、William Herschel Telescope(WHT)[9-11]等都对编码器类型、测角方案、测角误差源以及校正方案都做出了详细地理论分析和实验验证。通过对测量误差谐波特性的分析[12],正确认识误差的来源和特征可以有效消除或减小误差。本文基于拼接式钢带编码器的误差源进行分析,在文献[5]的基础上做了进一步的分析,提出了谐波分析幅值补偿方法。
2拼接式编码器测角误差分析与修正
根据编码器安装方式以及测角基本原理,可以将影响拼接式编码器测角的因素分为:系统误差,机械安装、零件加工误差及其它误差。温度不均匀引起的光栅尺不规则变形对测角误差影响较小,可忽略不计[13]。
2.1 机械加工和安装误差
机械加工和安装误差主要包括圆盘安装偏心、钢带安装圆环不圆度、光栅安装盘倾斜等,引入的测角误差谐波主要集中在低频区域。
2.1.1安装偏心引起的测角误差
偏心指钢带安装盘的几何中心与实际旋转中心之间的距离,图1为光栅偏心示意图。设光栅半径为R;光栅中心相对于旋转中心的偏心距为e;偏心与参考零位的夹角为0°。理想情况下(光栅中心与旋转中心重合),光栅转过角度φ时,读数头扫描区域应为理想圆上的一段圆弧S。
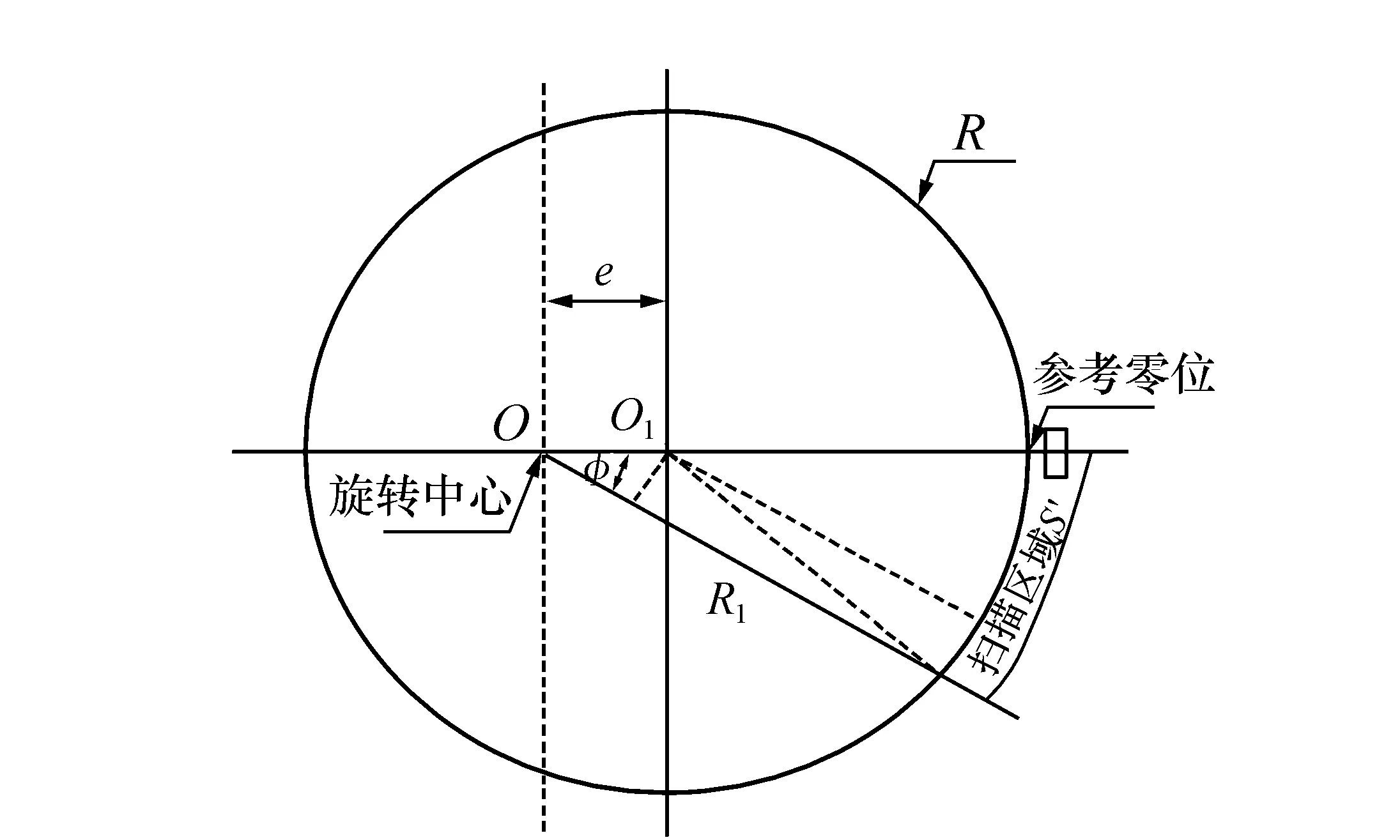
图1 安装偏心原理图 Fig.1 Schematic diagram of mechanical installation eccentricity
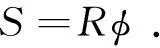
(1)
存在偏心时,读数头扫描区域S′已非理想状态下的圆弧。弧长等于半径乘以弧度,易知dS′=R1dφ,故采用积分法求这段弧长,R1为旋转中心至光栅表面的距离。对于任一转动角度φ,R1有如下表达式:
(2)
读数头扫描区域S′为:
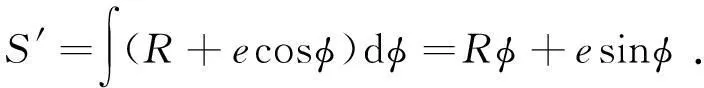
(3)
故由偏心引入的扫描区域弧长误差为:
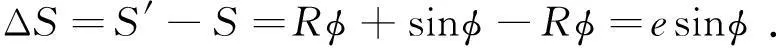
(4)
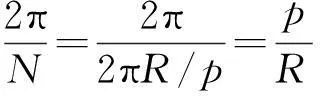
(5)
光栅尺直径为D=550 mm时,此时由于机械安装偏心e=5 μm,引起的测角误差为3.75″。
2.1.2钢带安装环圆度引起的测角误差
由于加工制造和安装的原因,拼接钢带安装后会产生圆度误差。受其影响,旋转中心至光栅表面的距离Rθ中增加了二阶以上的高次谐波,综合偏心作用,Rθ用谐波可表示为:
(6)

图2 钢带安装环椭圆度原理图 Fig.2 Schematic diagram of roundness error with cirque
则由光栅圆度引入的读数头扫描区域弧长误差为:
(7)
则由光栅圆度引入的测角误差为:
(8)
则各阶谐波产生的测角误差幅值为(单位:″):
(9)
由上可知,光栅圆度引起的误差谐波阶次越高,幅值越小,对光栅测角精度影响也越小。故这类误差主要集中在低频区域。
2.2 多读数头消差原理
采用多读数头消差技术,即沿光栅编码器圆周均布n个读数头,以消除由轴系晃动、光栅安装偏心和圆度等引起的中低频测角误差。在精密测角场合中,它是提高测角精度最普遍最有效的手段,而且具有实时补偿性。设被测轴的转角真值为θ,各读数头读出的角度值分别为θj,j=1,2,…,n,那么各读数头的测角误差Δθj:
(10)
由上式可知,编码器的测角误差可以表示为各次谐波量的合成。于是,各读数头的测量误差Δθj可表示为傅氏级数:
或
(11)
式中,M为测角误差谐波的最高阶数;Ai、Bi为第i阶谐波误差系数;Ci为第i阶谐波误差的振幅;φi为第i阶谐波的初相角。
均布n个读数头的读数平均值为:

(12)

(13)
交换求和次序,并应用两角和的三角公式,整理后得:
(14)
因为:
(15)
(i为≥1的任何整数)
则:
或
(16)
式中,m为≤M/n的正整数。
上式即是经多读数头消差技术后的测角误差。它只含有kn阶误差,已不再含有kn阶以上的各阶误差成分。因此,对径两读数头可以消除由偏心引入的一阶误差;均布四读数头可消除机械安装偏心误差和钢带安装圆环椭圆度误差。
在机械安装误差中一阶谐波与二阶谐波起主导作用,而对径读数主要用于消除一阶误差;两垂直读数头主要用于消除二阶误差。
(1)读数头不对径时消除一阶误差谐波的效果
设一阶误差幅值为C1,两读数头之间的角度为180°+ε,则经读数平均后的一阶谐波误差变为:
(17)
(2)读数头不垂直时消除二阶误差谐波的效果
设一阶误差幅值为C2,两读数头之间的角度为90°+ε,则经读数平均后的二阶谐波误差变为:
(18)
此时不垂直读数并未完全消除二阶误差谐波,幅值变为2sinε×C2。若ε=1°,则幅值为0.035C2。
3测角实验与分析
实验在某望远镜方位轴系转台上进行,测角组件由海德汉ERA8400C型拼接式钢带光栅尺和均布四个读数头组成,光栅直径为550 mm,系统分辨力为0.05″。标校系统采用23面体和自准直仪,如图3所示,对各读数头进行了编号,其中读数头1提供零位信号。

图3 测角实验原理图 Fig.3 Schematic diagram of angle measuring experiment
使方位转台沿逆时针和顺时针方向旋转分别测量钢带编码器的测角误差,其测角误差曲线如图4、图5,两组测角误差数值最大分别为8.51″、9.45″,两组测角实验合成误差的RMS分别为0.42″、0.59″。
根据前述理论分析可知,均布多读数头可以消除除kn阶以外的所有阶次误差谐波。故采用对径双读数头时合成误差谐波应呈现出阶次为1、3、5、7、9、11的谐波幅值明显降低;采用均布四读数头时合成误差谐波应呈现出阶次为1、2、3、5、6、7、9、10、11的谐波幅值明显降低。通过表1对顺时针方向测量的数据分析可以看出:除幅值显著较大的一阶和二阶谐波外,其余幅值较小的阶次似乎并不明显甚至不符合上述的消谐波特性。这里必须考虑到导致这种结果的原因:第一,受测量点数的限制,谐波分析法本身会带来谐量混杂影响,计算得出的每一阶次谐波按照一定规律混杂了其他阶次谐波。那么幅值较小的谐波,受其它谐量影响就较大。第二,幅值小的谐波易受到随机误差等因素影响。
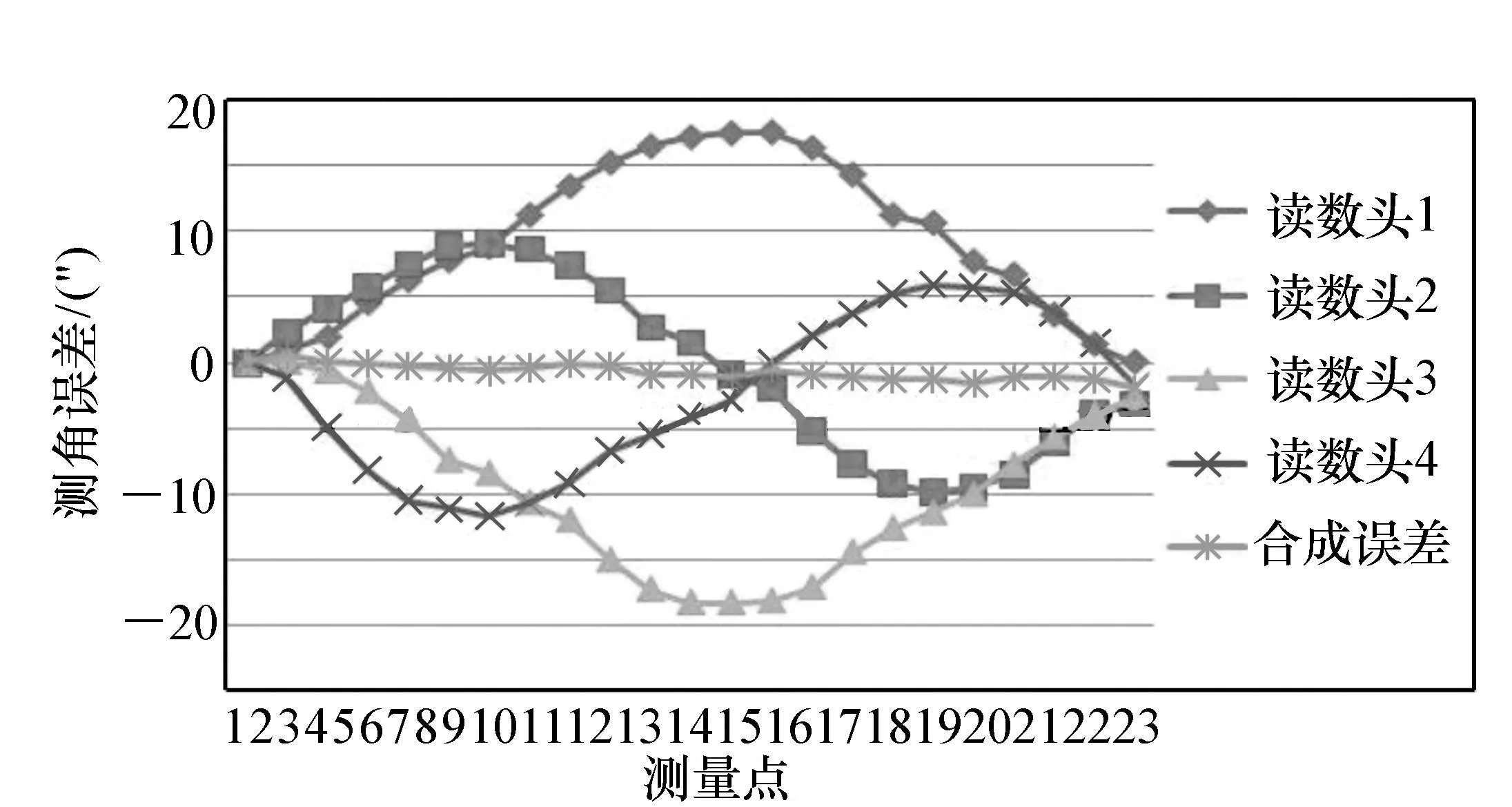
图4 逆时针方向读数头测角误差曲线 Fig.4 Angle measurement error curve for counterclockwise

图5 顺时针方向读数头测角误差曲线 Fig.5 Angle measurement error curve for clockwise
表1顺时针旋转不同读数头数目下的误差谐波幅值表
Tab.1Harmonic amplitude of different reading heads for clockwise rotation

(单位:〃)
下面选取顺时针旋转数据,分析读数头1与其余读数头之间的初相位关系,来验证各读数头的测角误差理论模型,进一步证明其消谐波特性[14]。由式(11)知,对于同一阶次谐波,读数头1与其余读数头的初相位差值为i×(j-1)×2π/4,其中i指谐波阶次,i=1,2;j指读数头序号,j=2,3,4。考察初相位表,比较读数头1与其余读数头的一、二阶谐波初相位。计算结果见表2,各读数头的一、二阶谐波曲线见图6、7。

表2 初相位理论差值与实际差值比较表

图6 顺时针方向读数头测角误差一次谐波 Fig.6 First harmonic of angle measurement error for clockwise

图7 顺时针方向读数头测角误差二次谐波 Fig.7 Second harmonic of angle measurement error for clockwise
由表2可知,对于一、二阶谐波,读数头1与其余读数头的初相位理论差值与实际差值较大。首先从谐波特性来考察光栅1的误差曲线图。若仅存在一阶误差谐波,那么读数头1的误差曲线应该与读数头3的误差曲线对称,读数头2与4的误差曲线应该对称。但是从图6、7中易看出,上述误差曲线并不对称,出现明显的相位偏差。因此我们推测测角误差含有幅值较大的二阶以上的谐波,导致了相位关系发生改变。分析误差谐波特性,观察表1,可以看到二阶谐波幅值远大于除一阶以外的其他阶次幅值,这种结果与上述推测一致。假定测角误差仅由一阶与二阶误差谐波组成,利用谐波分析拟合误差曲线,此时各读数头的误差曲线见图8。

图8 顺时针方向读数头测角误差拟合曲线 Fig.8 Fitted curves of angle measurement error for clockwise
4结论
本文采用相位差为90°的均布4读数头测角方式,从理论角度分析了拼接光栅机械安装偏心、圆度误差等对编码器测角的影响,然后分析了4读数头的消差原理。最后在某望远镜方位轴系转台上进行了逆时针和顺时针方向测角实验,对两组测角实验误差进行谐波分析,通过幅值补偿后RMS值分别为0.34″、0.38″,与未进行幅值补偿(文献[5])相比有明显改善。实验表明该方案和校正方法能消除由于钢带安装盘安装偏心、钢带安装盘圆度误差及部分系统误差等引起的测角误差,实现了亚角秒级精度的测角。由于读数头安装位置精度原因,使得分离出的高次谐波相位相差较大,还有待进一步研究,并进行相位补偿。本文可为未来大口径望远镜设计阶段的测角方案和误差分析与分配、预估测角精度,为降低设计和加工误差提供参考。
参考文献:
[1]MEEKS R L. Improving telescope mechanical error estimates using pointing data[D]. Fort Collins:Colorado State University,2003.
[2]王显军.反射式光电编码器[J].光学 精密工程,2013,21(12):3066-3071.
WANG X J. Reflection photoelectric encoder[J].Opt.PrecisionEng.,2013,21(12):3066-3071.(in Chinese)
[3]徐晓丹.增量式光电编码器细分技术研究[D].长春:长春理工大学,2009.
XU X D. Research of electronic subdivision of incremental shaft encoder[D]. Changchun:Changchun University of Science and Technology,2009.(in Chinese)
[4]高旭,万秋华,赵长海,等.莫尔条纹光电信号正交性偏差的实时补偿[J].光学 精密工程,2014,22(1):213-219.
GAO X,WAN Q H,HAO CH H,etal.. Real-time compensation of orthogonality deviation for Moire fringe photoelectric signal[J].Opt.PrecisionEng.,2014,22(1):213-219.(in Chinese)
[5]潘年,马文礼.拼接式钢带光栅编码器测角误差分析与修正[J].中国光学,2013,6(5):788-794.
PAN N,MA W L. The error analysis and correcting of scale tape grating encoder[J].ChineseOptics,2013,6(5):509-513.(in Chinese)
[6]王显军.光电轴角编码器细分信号误差及精度分析[J].光学 精密工程,2012,20(2):379-386.
WANG X J. Errors and precision analysis of subdivision signals for photoelectric angle encoders[J].Opt.PrecisionEng.,2012,20(2):379-386.(in Chinese)
[7]冯英翘,万秋华,王树洁.小型光电编码器长周期误差的修正[J].光学 精密工程,2014,22(9):2491-2497.
FENG Y Q,WAN Q H,WANG SH J. Correction of long-period error for small photoelectric encoders[J].Opt.PrecisionEng.,2014,22(9):2491-2497.(in Chinese)
[8]MANCINI D,CASCONE E,SCHIPANIL P. Galileo high-resolution encoder system[J].SPIE,1997,3112:328-334.
[9]RAVENSBERGEN M,MERINO R,WANG C P. Encoders for the altitude and azimuth axes of the VLT[J].SPIE,2479:322-328.
[10]CALLAHAN S,ASHBY D,HAIR T,etal.. The Large Binocular Telescope main axis encoders:mounting hardware, read heads, and tape installation[J].SPIE,2006,6267:3B1-3B11.
[11]FISHER M. A high resolution incremental tape encoder on the William Herschel Telescope[J].SPIE,1994,2199:889-900.
[12]赵人杰,马文礼.利用误差谐波补偿法提高拼接式钢带编码器测角精度[J].仪器仪表用户,2009,16(3):69-71.
ZHAO R J,MA W L. Improving the accuracy of new-type encoders using error harmonic compensation[J].ElectronicInstrumentationCustomer,2009,16(3):69-71.(in Chinese)
[13]张玉莲.传感器与自动检测技术[M].北京:机械工业出版社,2012.
ZHANG Y L.SensorwithAutomaticDetectionTechnology[M]. Beijing:China Machine Press,2012.(in Chinese)
[14]王明佳,武治国,徐大鹏,等.精确自动识别莫尔条纹方向的算法[J].中国光学,2011,4(5):509-513.
WANG M J,WU ZH G,XU D P,etal.. Accurate and automatic recognition of Moire fringe angle[J].ChineseOptics,2011,4(5):509-513.(in Chinese)

黄 龙(1990—),男,四川巴中人,博士研究生,主要从事大型望远镜轴系技术方面的研究。E-mail:cdhuanglong@163.com

潘 年(1987—),男,重庆忠县人,博士研究生,主要从事大尺寸光栅测角技术方面的研究。E-mail:wopannian@163.com

马文礼(1962—),男,吉林四平人,研究员,博士生导师,主要从事望远镜系统、微电子检测设备、线阵和面阵CCD光学拼接、低温光学系统、真空远红外光谱测量仪、空间相机内方位元素测量仪等方面的研究。E-mail:mawenli@ioe.ac.cn

黄金龙(1982—),男,四川渠县人,硕士,助理研究员,主要从事大型望远镜结构设计方面的研究。E-mail:huangjinlong8080@163.com
HUANG Long1,2, PAN Nian1,2, MA Wen-li1*, HUANG Jin-long1
(1.InstituteofOpticsandElectronics,ChineseAcademyof
Sciences,Chengdu610209,China;
2.UniversityoftheChineseAcademyofSciences,Beijing100049,China)
Abstract:According to the accuracy specifications of telescope goniometry, error sources of sacle tape grating encoder and the angle measuring principle of multi reading head are analyzed. A 4-reading heads angle measurement program which have 90° phase difference, have been developed. And we make counterclockwise and clockwise angle measuring experiments on an azimuth turntable of telescope through harmonic processing and error compensation, and two sets of experiments measuring angle error RMS values of 0.42″ and 0.41″ are obtained. Experiment results show that the effect of shafting errors, processing error of installation position and partly roundness error for installation torus on the angular measurement accuracy is eliminated by harmonic processing and phase difference method, and high precision angle measurement with sub-arc-second-accuary is achieved. The research results are useful for analyzing and distributing errors, forecasting angle measuring accuracy and reducing design and machining errors in the design of large aperture telescopes.
Key words:scale tape grating encoder;angular measurement accuracy;harmonic analysis;telescope
作者简介:
*Corresponding author, E-mail:mawenli@ioe.ac.cn
中图分类号:TH741; TP762
文献标识码:A
doi:10.3788/CO.20150803.0464
文章编号2095-1531(2015)03-0464-07
基金项目:国家自然基金资助项目(No.60978050)
收稿日期:2014-12-15;
修订日期:2015-02-19
