云南地区中强地震前应变释放特征

钱晓东 李 琼 洪 敏

（中国昆明650224云南省地震局）



云南地区中强地震前应变释放特征

（中国昆明650224云南省地震局）

利用云南区域台网地震目录资料， 以地震应变能作为地震释放量度， 基于应变释放加速模型对前兆地震序列进行非线性模拟． 结果表明: 云南地区1966—2013年发生的115例MS≥5.0地震中， 具有加速特征的有79例， 占69%； 具有减速特征的有28例， 占24%； 数据太少无法判断加减速特征的有8例， 占7%． 主震为孤立型的前兆地震序列， 其减速或数据少类型所占比例远大于加速型； 主震为走滑型的前兆序列， 其加速型序列要比主震为正断型或逆冲型序列多15%左右． 搜索半径与前兆序列持续时间呈反比关系． 对前兆地震序列模拟结果表明， 主震的预测震级和时间误差为±0.3和0.5年．

应变释放加速 幂指数 中短期预测 云南地区

引言

类临界破裂点模型是将地震孕育过程看作是地球内部的一种临界破裂现象， 近年来得到国外地震学家的广泛关注（Main， 1995; Ben-Zionetal， 2003）． 作为临界性的表现， 大地震前会出现地震能量或地震矩释放加速过程， 其表现与凝聚态物理中某些参量在临界点附近的变化相似（Sornette， Sammis， 1995； Jaumè， Sykes， 1999）. 采用这种破裂模式对一些震例进行研究已取得明显效果， 并在地震预测预报领域显现出其应用潜力（Sykes， Jaumé， 1990； Bufe， Varnes， 1993; Bowmanetal， 1998； Brehm， Braile， 1998， 1999）． 国内相关研究成果的报道也逐渐增多． 蒋长胜和吴忠良（2009）以及蒋长胜等（2004）对中国大陆1978年以来109例M≥5.7地震进行加速矩释放（accelerating moment release， 简写为AMR）模拟， 发现震前矩加速释放是一种普遍现象， 并认为AMR现象可以作为一种可靠的、 带有普遍性的地震前兆用于地震预测实践； 蒋海昆等（2009b）将中国大陆M7.0地震前中小地震应变释放细分为5类， 详细分析了这些大地震前的应变释放特征， 结果显示呈加速特征的前兆序列所占比例最高； 杨文政等对中国大陆M≥5.0地震前兆事件的非线性加速现象进行研究（杨文政， 马丽， 1999； 杨文政等， 2000）， 该研究结果对主震震级和发震时间的预测取得较好效果； 秦嘉政和钱晓东（2004）采用破裂时间法对云南地区破坏性地震的研究结果表明， 震前出现加速现象的前兆序列所占比例高达80%． 在应变加速释放机理研究方面， 蒋海昆等（2009a）利用花岗岩实验数据， 研究声发射事件的应变释放特征， 模拟地球内部温度和压力环境， 结果表明深部环境下有应变释放加速现象， 幂指数m值明显低于浅表地层温压环境; 左兆荣等（1996）认为地震释放加速是成核过程的一个属性， 是地震失稳破裂的一个必要条件．

国内外地震科研人员对地震临界破裂模型的研究取得了丰富的成果， 在地震应变的加速释放机理、 加速释放的普遍性、 幂指数m值的特性、 资料时空范围的选取、 加速释放与后续强震的关系等方面均有涉及． 如何基于这一模型进行预测研究， 使之成为一种可靠的强震中短期预测方法， 尤其是应变加速释放与后续强震关系方面的研究尚需从多方面进行深入、 持续的探索．

本文拟通过对云南地区大量M≥5.0中强地震的应变释放临界破裂特征进行回溯， 详细研究应变加速释放理论， 给出具体操作步骤， 并对一些基本问题进行深入探讨， 力求在一定程度上揭示前兆地震事件活动的某些特征， 尝试开展地震中短期预测实验．

1 应变释放加速模型

破裂时间理论由Das和Scholz（1981）根据材料力学理论提出， 之后Varnes（1989）根据破裂时间理论将破裂时间函数定义为

（1）

式中Ω为地震活动性的量度， 可以是地震频度、 地震能量、 地震矩等表示地震强弱状态的量度；t为地震的发生时间；tf为主震发生时间， 亦称为破裂时间， 表示临界点时间；k和n为常数． 对式（1）积分， 给出方程的一般形式（Bufe， Varves， 1993）为

∑Ω=A+B（tf-t）m，

（2）

式中用累积量∑Ω表示地震活动的强弱程度，A和B为常数， 幂指数m称为标度常数．

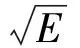
lgE=1.5MS+4.8，

（3）

应变释放加速模型表示为

（4）

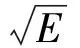
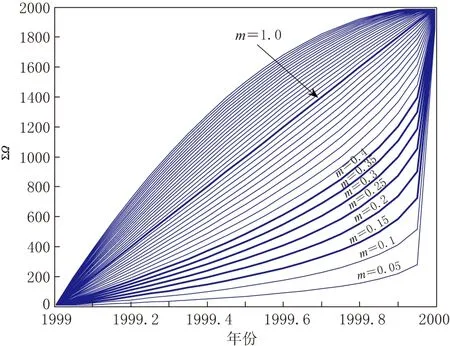
图1 ∑Ω-t曲线图

式（2）中标度常数m是一重要参数， 它表征了地震应变释放曲线的类型． 图1给出了不同m值时∑Ω-t曲线的形态， 可以看到m<1时曲线为加速形态，m>1时为减速形态，m=1时曲线变为直线． 进一步讨论曲线为加速形态的情况： 当m<1时， 不同m值所对应曲线的加速程度不同，m<0.1时曲线虽然表现为加速， 但是曲线较为平缓， 表明曲线加速程度较低， 因此可以认为m<0.1时表明地震相对平静， 地震释放间隔相对较长， 释放量较低， 这种情况下序列加速不理想；m>0.4时， 曲线向直线靠拢， 表明虽然地震较为活跃， 但地震的释放量均匀、 增长不明显， 这种情况与m<0.1时一样， 序列加速不理想； 当0.1≤m≤0.4时加速曲线的曲率最大， 表明随着时间的推移， 地震释放的时间间隔越来越短， 释放量越来越大， 这种情况下序列加速较为理想， 尤其是0.15≤m≤0.3时曲线加速现象更为明显．

2 资料和模拟结果

2.1 资料选取

云南是多震地区， 平均每年发生M≥5.0地震3次． 1966年1月—2013年12月的48年间， 云南发生M≥5.0地震155次， 其中包括双震的后一次地震和震群的第二次及以后地震． 将双震、 震群看作一次独立主震事件， 以本文得到的115次M≥5.0地震作为震例进行研究， 震中分布见图2中蓝色大圆圈， 这些地震涵盖了这一时期独立的M≥5.0主震事件.

为保证模拟结果的可靠性， 统计样本的选取原则和限定条件约定如下：

1） 本文使用的地震资料是云南省地震局提供的1965年以来云南及附近地区的中小地震正式地震目录， 并且已进行了地震目录的完整性分析． 根据苏有锦等（2003）对该地震目录的研究， 金沙江断裂、 红河断裂带以西的滇西、 滇西南地区的腾冲、 龙陵、 澜沧、 耿马、 思茅、 普洱地区， 1981年以前控制震级为Mc3.0， 1982年以后为Mc2.5， 其余地区控制震级为Mc2.5． 图3为当时震级控制能力较低的滇西、 滇西南地区1970年1月—1979年12月的G-R关系图， 可见累计频度与震级关系的拐点在M2.5处， 但单一震级频度与震级关系却显示控制震级为Mc3.0． 根据Brehm和Braile（1998）提出的地震序列控制震级判别准则， 地震目录完整震级至少要包括比主震震级小2个震级单位的地震． 因此， 本文考察的主震（MS≥5.0）若处于滇西和滇西南地区且发震时间在1981年以前， 则前兆序列的控制震级最小取Mc3.0．

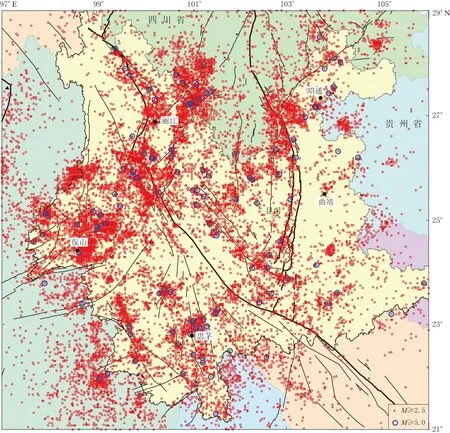
图2 1965年1月—2013年12月云南地区的地震分布

图3 1970年1月—1979年12月滇西和滇西南地区G-R关系

通过统一震级标度将震级统一到MS．MS≥5.0地震都有MS震级可直接选取， 目录中既有MS又有ML的地震取MS， 目录中无MS的M<5.0地震按适用云南地区的地震标定律进行转换（秦嘉政等， 2005）：

MS=1.5ML-2.4.

（5）

2） 要有足够的地震数， 即规定前兆序列地震次数大于10， 且在前兆时间段内最好均匀分布．

3） 前兆地震序列持续时间的确定． 当主震震级与序列中除主震之外的最大地震震级之差大于等于0.6时， 此最大地震后一地震至主震时间称为前兆地震序列持续时间， 即前兆序列中不允许有与主震震级相差小于0.6的地震出现， 否则作为新的序列考虑． 本文将震级差0.6作为序列截断依据， 主要根据中国地震局（1998）对主震余震型、 双震型等地震序列的判定以震级相差0.6为标准的定义． 此外，Brehm和Braile（1999）也将震级差0.6作为前兆地震序列持续时间的序列截断震级．

4） 由于云南地区地质构造纵横交错， 地震类型复杂， 不同区域余震的持续时间、 分布范围存在较大差异， 故本文采用比较可靠的手工删除余震方法来删除MS>5.0地震的余震. 一般规则和操作方法为： 首先确定余震的空间范围， 可从序列震中分布图直接目测获得； 其次， 确定序列的持续时间， 将余震区震前和震后的地震取出， 绘制日频度， 对于震前地震活动相对活跃的地区， 序列衰减至主震前活动水平所对应的时间即为余震持续时间， 而对于震前地震活动相对较弱的地区， 当序列频度衰减至每日仅发生1次地震时的相应时间则可作为余震序列的持续时间（周蕙兰等， 1982）； 最后， 删除余震空间范围在余震持续时间内的地震． 图2中红色圆圈为删除余震后的地震．

2.2 模拟结果

表1给出了1966年1月—2013年12月云南发生的主震事件的基本参数和模拟结果． 对于每一次主震事件， 围绕主震震中进行前兆中小地震时间和空间搜索． 空间区域搜索半径R范围为30—300 km， 10 km为步长． 30 km约为一次MS5.5地震破裂半径的3倍， 约相当于一次MS5.0地震的余震分布范围． 搜索时间t的范围为1965年到主震发生的时间， 步长为1个月． 具体步骤如下：

表1 主震事件参数和模拟结果Table 1 Parameters of main shock events and simulation results

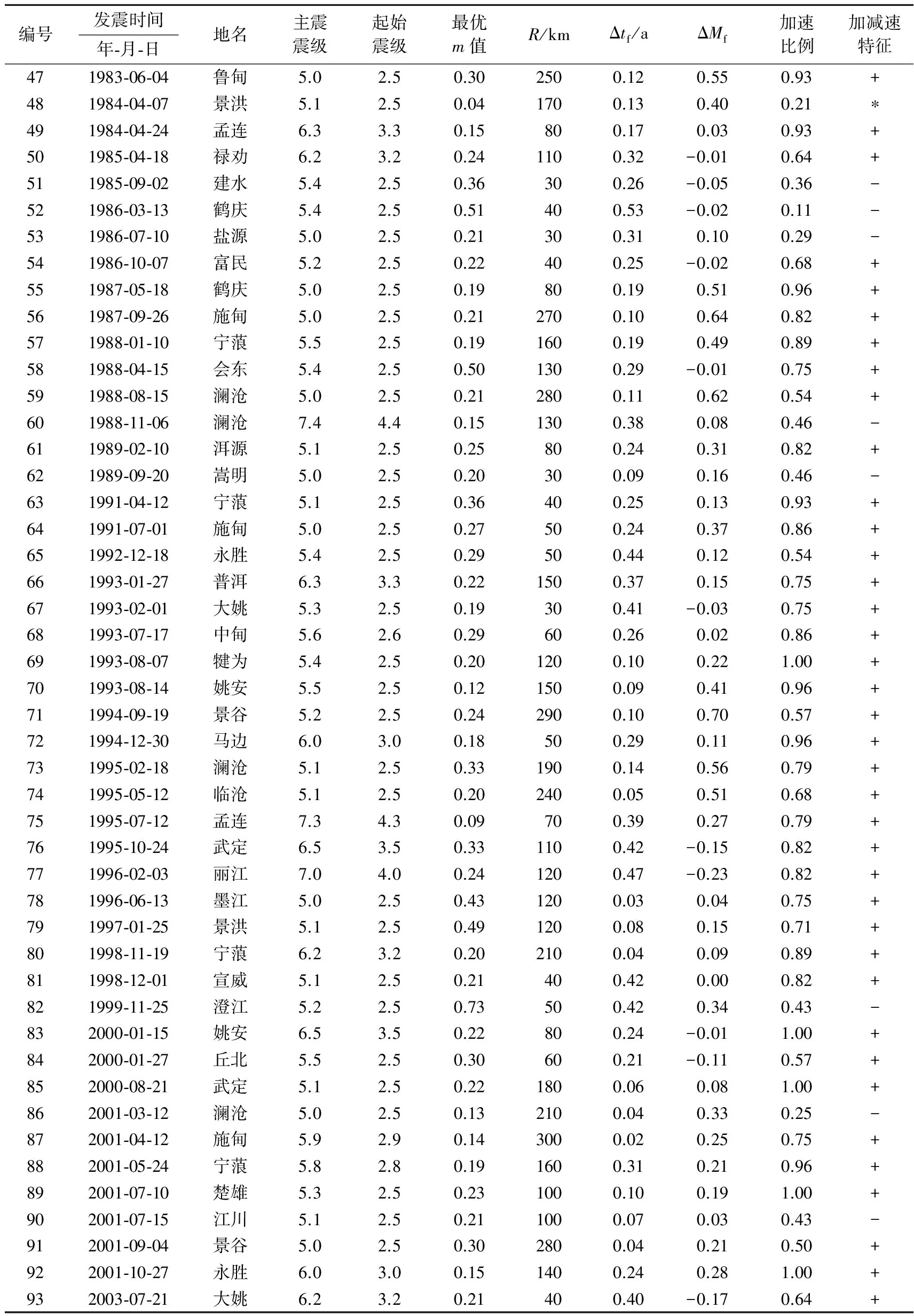
续表1

续表1

1） 搜索出一定空间区域的起始时间． 取一定搜索半径R， 以1个月为步长滑动， 在资料起始时间至主震时间范围内进行应变释放曲线模拟． 不同搜索时间得到相应标准差S， 其最小值对应的时间即为最佳搜索时间t． 标准差S定义为

（6）

根据应变释放加速模型式（4）进行模拟， 采用穷举非线性最小二乘求解方法． 指定m∈[0， 5]， 以0.01为步长进行穷举. 对于每一个固定的m， 使式（4）变为直线， 从而求得相应的常数A和B及标准差S， 取最小标准差对应的曲线为拟合结果．

2） 搜索出全部时空范围内的最终拟合曲线． 由第一步得到一定搜索半径R所对应的最佳搜索时间t，R在30—300 km范围内取值， 以10 km为步长滑动， 得到每一次搜索半径R对应的一系列最佳搜索时间t， 如图4a所示． 为了从众多曲线中挑选出最优的一条， 采用m值结构分析与曲线曲率参数C值相结合的方式．C值定义为（蒋海昆等， 2009b）

（7）

式中SL为直线标准差，SC为曲线标准差. 当C=1时前兆序列应变释放为直线； 当C>1时， 表明幂律（曲线）拟合结果优于直线拟合，C越大， 曲线弯度越大， 曲线加速愈明显； 当C<1时表明幂律拟合结果较直线拟合误差大．

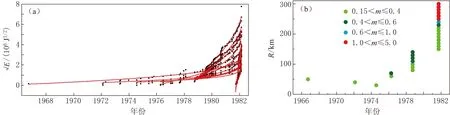
图4 1982年2月20日江城MS5.0地震前时间搜索得到的应变释放曲线及其参数实例

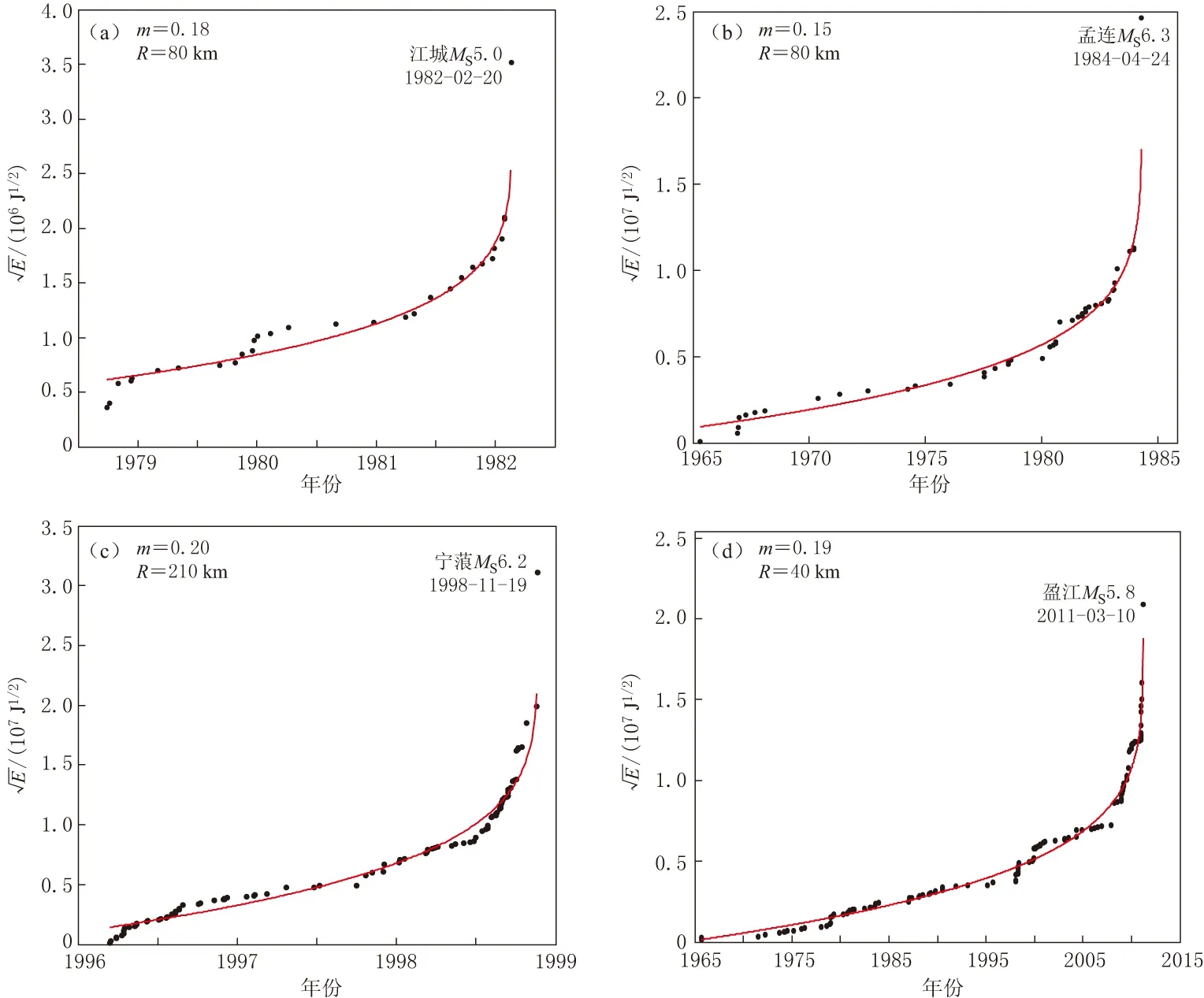
图5 4次应变释放加速曲线震例

由于本文采用的时间、 空间自动搜索得到许多拟合结果， 加之不同组数据分布差异较大， 对C值的影响较大． 若单纯取最大C值所对应的曲线为最优曲线， 得到的结果则不甚理想． 因此， 需先对获得的一系列不同m值的分布特征进行分析， 确定m值的分布范围， 然后再选取这一范围内最大C值对应的曲线为最终拟合曲线．

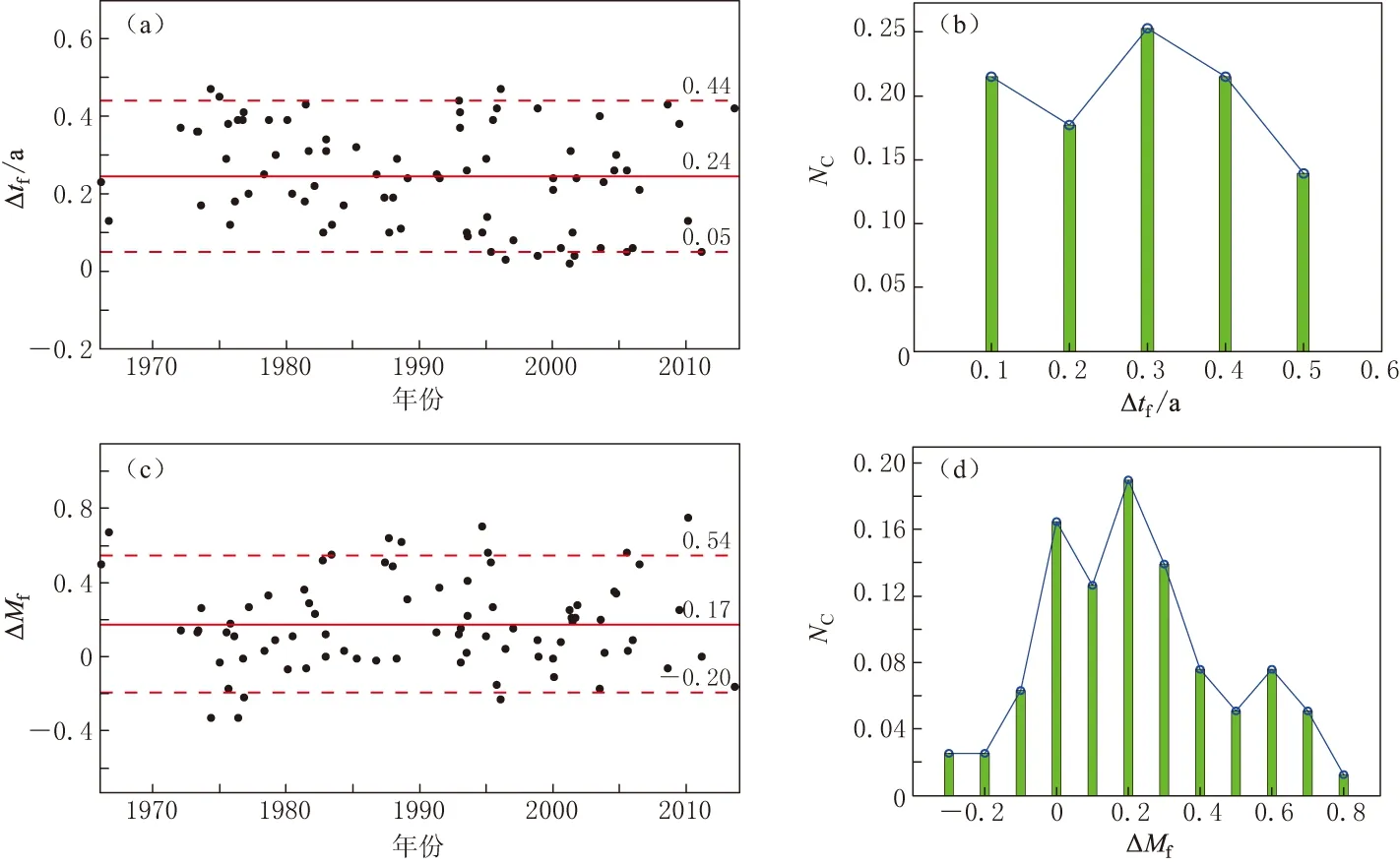
根据上述分析， 当0.1≤m≤0.4时加速曲线的曲率较大， 尤其是0.15≤m≤0.3时曲线加速比较明显． 从图4a江城MS5.0地震震例看到， 当搜索的起始时间t在1978年之前时， 虽然也能得到m值处于理想范围的曲线， 但这样的曲线较少且分散， 搜索范围也较小（R<100 km）（图4b）; 当搜索的起始时间达到1978年时，m值处于理想范围的曲线大量密集出现， 当0.1

3 主震时间和震级的预测

3.1 预测时间tf和预测震级Mf

图5是在主震震级和发震时间不变的情况下构建的应变释放加速曲线， 当主震震级和发震时间发生改变时曲线是否会发生相应变化呢？ 换言之， 在前兆地震事件不变的情况下， 改变主震发震时间和震级得到的加速曲线的误差， 与实际主震情况下的误差之间相差多少呢？ 这是应变释放加速模型进行实际地震预测的关键．

回答上述问题采取主震震级和时间扫描方法． 预测震级Mf和预测时间tf定义为每次扫描的震级和时间． 每次扫描可以构建标准差S误差图．Mf取值为主震震级±2， 步长为0.1；tf取值为主震后1年， 步长为10天． 根据不同tf和Mf值以及式（4）可以求得应变释放曲线， 并从式（5）计算出相应的标准差S， 进而得到标准差S等值线图（图6Ⅰ）． 低S区域代表最佳拟合解集， 其形状总体呈“V”字形或“带”状形， 从图6Ⅰ中可以看到， 最小S区域范围过大， 收缩、 指向性不明显， 最小值区域与实际主震事件发生的时间和震级的关系难以进行定量化评估， 与Brehm和Braile（1998）的研究结果相类似．

为了改善预测效果， 我们重新构建每次主震事件预测时间和预测震级的S值等值线图． 虽然图6Ⅰ中S最小值区域面积大、 空间收敛性不强， 但实际上S最小值区域内的每个点都对应于一条从众多拟合曲线中挑选出来的曲线， 因而可以取S最小值区域几何中心点坐标作为初始预测时间和震级， 通过固定相应m值的方式重新计算S值等值线图（图6Ⅱ）． 可以看出， 图6Ⅱ中S最小值区域收缩性更好， 模拟主震的实际值几乎落入所构建的标准误差图最小值区域内， 图像形态与Wang和Shieh（2004）结果相似． 图6Ⅱ中全局最小值时间和震级与实际主震时间和震级之差定义为预测时间误差Δtf和震级误差ΔMf， 详见表1．

图6 归一化标准差S等值线影像图

3.2 预测时间和预测震级的误差

表1所给出的115次主震事件用应变释放加速模型模拟的预测时间tf和预测震级Mf的误差结果， 代表的是固定指数m为约束的拟合结果（图6Ⅱ）． 由于所有主震前均能搜索出应变释放加速曲线， 表1也给出了减速、 数据少序列的预测结果， 减速、 数据少序列选取的是其加速曲线中曲率较大的曲线． 时间和震级的预测误差为预测值减去实际值．

图7给出了所有模拟加速序列的预测时间和预测震级的误差统计图， 实线为均值， 虚线为均值加减1.5倍方差． 从预测时间来看（图7a， b）， 均值为0.24年， 数据分布在0.1—0.5年之间. 由于误差为预测值减实际值， 预测误差分布表明预测值比实际值大， 误差在0.5年以内．

从预测震级来看（图7c， d）， 均值为0.17， 数据主要分布在-0.2—0.5之间， 与均值偏差约±0.3． 秦嘉政和钱晓东（2004）采用k/m经验关系限制m值的方法对云南30次主震事件用破裂时间法模拟预测时间和预测震级， 得到的时间误差约±0.64年、 震级误差约为±0.57， 本文结果预测时间和预测震级的精度在此基础上有所提高， 因此对半年尺度的中短期预测是有效的．

图7 预测时间和预测震级的误差统计

4 应变释放的加速和减速

从本文关于云南地区MS≥5.0地震应变释放的模拟结果来看， 以主震为中心进行震前应变能曲线的时间、 空间扫描和模拟， 所有主震前均能搜索出应变释放加速曲线， 也能够得到唯一m值（表1）以及各项模拟参数． 但是， 不同主震搜索出的加速曲线的数量却存在较大差异． 对于不同搜索半径R， 当m<1的加速曲线数量占全部搜索数量的比例NC>50%时， 表明加速曲线占较多数， 这次地震则称为加速序列（表1中用“+”表示）； 当m≥1的曲线数量占全部搜索数量的比例NC>50%时， 表明减速曲线占较多数， 这次地震序列则称为减速序列（表1中用“-”表示）； 由于震前地震较少（小于10次）或有干扰事件影响不能很好拟合出结果， 这种情况出现的比例NC>70%时， 这次地震序列则称为数据少序列（表1中用“*”表示）．

图8给出了地震序列分别为加速、 减速和数据少的例子． 图8a为1982年2月20日江城MS5.0地震， 当搜索半径R从30 km变化至300 km， 步长为10 km， 共进行了28次搜索， 每一次搜索再进行时间扫描可得到一个m值． 可以看到： 当搜索半径R<230 km时， 绝大多数m值在0.2—0.6之间，m<1的点有22次； 当R>230 km时，m>1，m值显示序列加速的比例为22/28=79%， 因此判定此次序列为加速序列． 图8b为1999年11月25日澄江MS5.2地震， 可以看到m值整体偏大，m<1的点多数在0.8附近（12次）， 加速比为43%， 故判定此次序列为减速序列． 图8c为1968年6月13日麻栗坡MS5.2地震， 当R值在200 km以内搜索时， 由于地震较少， 未达到10次， 因此不能得到有效m值； 随着R的增大， 地震逐渐增多， 得到5次加速曲线； 当R>260 km时， 1967年1月14日中越边境（震中位置为21.8°N、 103.2°E， 与主震相距260 km）发生MS4.7地震， 由于其震级与主震震级相差0.5， 被视为干扰事件， 因而无m值， 该次震例不能获得结果的情况所占比例高达82%， 故判定此次序列为数据少序列．

图8 加减速序列搜索半径R与m关系

根据上述判定原则， 115次震例中， 加速序列为79次， 占69%； 减速序列为28次， 占24%； 数据少序列为8次， 占7%． 蒋长胜等（2004）对中国大陆109例M≥5.7地震进行矩释放加速研究， 保守估计50%、 乐观估计77%具有加速释放现象， 具有减速特征的占21%， 数据太少无法判断的占8%． 本文研究与其结果相近．

5 讨论与结论

准确地识别前兆序列持续时间十分困难， 本文采用的时间扫描最优m值方法， 虽然能做到在人工无干预情况下给出定量唯一的开始时间， 但是这一结果是基于对一定范围m值搜寻和加速曲线分布结构的分析而得到的， 最终结果势必舍弃一些存在加速现象的起始时间． 一般认为， 大震级地震需要更多的能量积累， 期望获得的持续时间较长， 但根据我们得到的云南地区应变释放持续时间与主震震级关系来看， 震级越大持续时间越长的现象并不明显， 持续时间最短1年， 最长可达30—40年， 持续时间较长的地震震级为MS5.5—6.5，MS≥7.0地震除1970年通海MS7.8地震由于资料时间短以外， 持续时间均在10—30年之间， 未出现低于10年的情况， 似乎有MS≥7.0地震的前兆序列持续时间不会太短的现象．

从搜索半径与主震震级关系分析， 一般认为地震越大， 孕震区域范围越大， 期望得到搜索半径与主震震级成正比现象， 但从本文得到的结果来看， 这种现象并不明显， 震级在MS5.5—6.5范围时搜索半径在50—300 km均有分布， 小震大范围或大震小范围现象均会出现． 当MS>6.6后， 除了1995年7月12日孟连MS7.3地震以外（搜索半径70 km）， 其它地震的搜索半径都大于130 km， 表明强震、 大震的孕震区域不会太小． 孟连MS7.3地震出现较小搜索半径， 可能与该地震有较多前震有关（震前在震中附近分别发生1995年6月30日MS5.5、 7月10日MS6.2两次较大前震）， 使得该前兆序列不需进行太多搜索就能获得较多应变释放加速曲线．

出现主震震级与前兆序列持续时间和搜索半径线性关系不明显的现象， 其主要原因可能与当地地震活动强弱有直接关系． 若某一地区地震活动较强， 或震前有明显地震活动甚至有前震， 则搜索半径将会较小， 与主震震级无关． 云南的地震活动不同区域、 不同时间差别很大． 对同一区域相同震级的主震而言， 有的时间段主震前小震活动频繁， 有的时间段则平静后发震； 而对不同区域相同震级的主震而言， 有的区域主震前小震活动频繁， 有的区域则平静发震． 因此容易出现主震震级与前兆序列持续时间和搜索半径线性关系不明显的现象．

图9 搜索半径R与持续时间Δt关系

搜索半径R与前兆序列持续时间Δt呈反比关系（图9）． 当搜索半径R较小（R<80 km）时， 会出现较多的持续时间较长的前兆序列（Δt>30年）; 当R增加至90—130 km时， 持续时间减小至10—20年;当R进一步增加（R>130 km）时， 除3次序列持续时间在10年左右外， 绝大多数前兆序列持续时间均在5年以内．

应变释放加速机理和成因有待进一步研究． 从本文震例初步研究来看， 应变释放模式与主震破裂机制（走滑型、 正断型、 逆冲型）或地震序列类型（主余型、 孤立型、 震群型）有一定相关性． 例如， 主震为孤立型的前兆地震序列， 应变释放为加速型的比例较少（14%）， 反而减速型或数据少类型占较大比例（86%）; 主震为走滑型的前兆序列， 加速型所占的比例要比主震为正断或逆冲型多， 前者所占比例为70%， 后者为55%． 由于资料和震例数量的限制， 这样的统计可能并不全面． 整体来看， 与应变加速释放机理相关的突出因素， 目前尚未得到明确认识．

大量岩石破裂实验（余怀忠等， 2004; 蒋海昆等， 2009a）表明， 岩石破裂前应变能会出现加速过程， 这种现象与地震前出现的能量加速现象相似. 本文所研究的应变释放加速模型， 是定量化研究震前应变能加速释放的重要手段， 在地震预测预报方面具有广阔前景， 但要真正实现有效预测预报还有很多困难． 此外， 对于约20%的震前能量均匀或减速释放的序列， 本文方法并无预测能力， 这是今后研究的一个方面. 该方法在预测上具有不唯一性， 目前研究认为震前围绕震中附近地震的应变能会普遍出现加速现象， 但是， 是否只要出现较为理想的应变加速释放就一定会发生地震呢？ 该方面的研究进展相对较缓， 对其进行深入研究是长期面临的课题．

本文采用应变加速释放方法对云南100多次地震进行总结， 是建立在实际主震已知的基础上， 在未知主震情况下的实际地震预测预报中如何应用呢？ 由于对固定的前兆地震事件而言， 主震震级不同， 其对应的加速曲线不同， 因而可先确定要预测区域范围的震级大小， 再进行空间扫描求出各空间点的m值， 而后根据m值的特性， 判断地震危险性较高的潜在地区． 另外， 还可基于应变加速释放模型建立空间网格搜索技术， 根据已发生的中小地震资料拟合一系列搜索半径， 通过分析搜索半径的空间分布特性， 确定未来主震可能发生的危险地点．

本文研究结果表明， 在115例震例中， 存在应变释放加速现象的震例有79例， 占69%； 因数据少无法判断序列为加速或减速的有8例， 占7%； 出现减速现象的有28例， 占24%． 由此可见， 云南地区MS≥5.0地震前， 中小地震出现应变释放加速现象具有一定普遍性． 此外， 通过降低曲线拟合误差对主震发生的时间和震级进行预测， 预测震级和预测时间误差为±0.3和0.5年．

蒋长胜， 吴忠良， 史勇军. 2004. 中强震前地震活动矩释放加速现象（AMR）的普遍性问题[J]. 中国地震， 20（2）: 119--125.

Jiang C S， Wu Z L， Shi Y J. 2004. Generality of accelerating moment release （AMR） before moderately strong earthquakes[J].EarthquakeResearchinChina， 20（2）: 119--125 （in Chinese）.

蒋长胜， 吴忠良. 2009. 强震前“加速矩释放”（AMR）现象: 对一个有争议的地震前兆的回溯性震例研究[J]. 地球物理学报， 52（3）: 691--702.

Jiang C S， Wu Z L. 2009. Accelerating moment release （AMR） before strong earthquakes: A retrospective case study of a controversial precursor[J].ChineseJournalofGeophysics， 52（3）: 691--702 （in Chinese）.

蒋海昆， 吴琼， 董祥， 苗青壮， 宋金. 2009a. 不同温压条件下声发射应变能释放特征： 加速模型参数物理含义的初步讨论[J]. 地球物理学报， 52（8）: 2064--2073.

Jiang H K， Wu Q， Dong X， Miao Q Z， Song J. 2009a. Behaviors of AE strain release under the different temperature and pressure condition: Discussion on the physical meanings of ASR model parameter[J].ChineseJournalofGeophysics， 52（8）: 2064--2073 （in Chinese）.

蒋海昆， 苗青壮， 董祥， 吴琼， 黎明晓， 宋金. 2009b. 中国大陆7级强震前中小地震应变释放特征[J]. 地震， 29（3）: 1--11.

Jiang H K， Miao Q Z， Dong X， Wu Q， Li M X， Song J. 2009b. Characteristics of strain release beforeM7 earthquakes in mainland China[J].Earthquake， 29（3）: 1--11 （in Chinese）.

秦嘉政， 钱晓东. 2004. 利用前兆事件对云南地区地震进行中短期预测研究[J]. 地震学报， 26（2）: 140--150.

Qin J Z， Qian X D. 2004. Study on medium-short term earthquake forecast in Yunnan Province by precursory events[J].ActaSeismologicaSinica， 26（2）: 140--150 （in Chinese）.

秦嘉政， 皇甫岗， 钱晓东. 2005. 云南强震活动与预测方法研究[M]. 昆明: 云南科技出版社: 310--315.

Qin J Z， Huangfu G， Qian X D. 2005.StudyonStrongEarthquakeActivityinYunnanandPredictionMethods[M]. Kunming: Yunnan Science and Technology Press: 310--315 （in Chinese）.

苏有锦， 李永莉， 李忠华， 易桂喜， 刘丽芳. 2003. 川滇地区区域地震目录完整性最小震级分析[J]. 地震研究， 26（增刊）: 10--16.

Su Y J， Li Y L， Li Z H， Yi G X， Liu L F. 2003. Analysis of minimum complete magnitude of earthquake catalog in Sichuan-Yunnan region[J].JournalofSeismologicalResearch， 26（Suppl）: 10--16 （in Chinese）.

杨文政， 马丽. 1999. 地震活动加速模型及其在中国的应用[J]. 地震学报， 21（1）: 32--41.

Yang W Z， Ma L. 1999. Seismicity acceleration model and its application to several earthquake regions in China[J].ActaSeismologicaSinica， 21（1）: 32--41 （in Chinese）.

杨文政， Vere-Jones D， 马丽， 刘杰. 2000. 一个关于临界地震的临界区域判别的方法[J]. 地震， 20（4）: 28--38.

Yang W Z， Vere-Jones D， Ma L， Liu J. 2000. A method for locating the critical region of a future earthquake using the critical earthquake concept[J].Earthquake， 20（4）: 28--38 （in Chinese）.

余怀忠， 尹祥础， 夏蒙棼， 许昭永， 李敏， 梁乃刚， 彭克银， Kukshenko V， Elizarov S. 2004. 地震临界点理论的实验研究[J]. 地震学报， 26（增刊）: 122--130.

Yu H Z， Yin X C， Xia M F， Xu Z Y， Li M， Liang N G， Peng K Y， Kukshenko V， Elizarov S. 2004. Experimental research on critical point hypothesis[J].ActaSeismologicaSinica， 26（Suppl）: 122--130 （in Chinese）.

中国地震局. 1998. 地震现场工作大纲和技术指南[M]. 北京: 地震出版社: 25--26.

China Seismological Bureau. 1998.Outlinesofon-the-SpotWorkonEarthquakesandTechnologyGuide[M]. Beijing: Seismological Press: 25--26 （in Chinese）.

周蕙兰， 房桂荣， 章爱娣， 姜长宁. 1982. 余震序列的持续时间[J]. 地震学报， 4（1）: 45--54.

Zhou H L， Fang G R， Zhang A D， Jiang C N. 1982. The duration of the aftershock sequence[J].ActaSeismologicaSinica， 4（1）: 45--54 （in Chinese）.

左兆荣， 张国民， 吴建平. 1996. 1976年云南龙陵7.4级地震序列分析[J]. 地球物理学报， 39（5）: 653--659.

Zuo Z R， Zhang G M， Wu J P. 1996. Analysis of the 1976 Longling， Yunnan， earthquake sequence ofMS7.4[J].ChineseJournalofGeophysics， 39（5）: 653--659 （in Chinese）.

Benioff H. 1951. Earthquakes and rock creep. Part Ⅰ: Creep characteristics of rocks and the origin of aftershocks[J].BullSeismolSocAm， 41（1）: 31--62.

Ben-Zion Y， Eneva M， Liu Y F. 2003. Large earthquake cycles and intermittent criticality on heterogeneous faults due to evolving stress and seismicity[J].JGeophysRes， 108（B6）: 2307. doi:10.1029/2002JB002121.

Bowman D D， Ouillon G， Sammis C G， Sornette A， Sornette D. 1998. An observational test of the critical earthquake concept[J].JGeophysRes， 103（B10）: 24359--24372.

Brehm D J， Braile L W. 1998. Application of the time-to-failure method for intermediate-term prediction in the New Madrid seismic zone[J].BullSeismolSocAm， 88: 564--580.

Brehm D J， Braile L W. 1999. Intermediate-term earthquake prediction using the modified time-to-failure method in southern California[J].BullSeismolSocAm， 89（1）: 275--293.

Bufe C G， Varnes D J. 1993. Predictive modeling of the seismic cycle of the Greater San Francisco Bay region[J].JGeophysRes， 98（B6）: 9871--9883.

Das S， Scholz C H. 1981. Theory of time-dependent rupture in the earth[J].JGeophysRes， 86（B7）: 6039--6051.

Gutenberg B， Richter C L. 1956. Magnitude and energy of earthquakes[J].AnnGeofis， 9（1）: 1--15.

Jaumé S C， Sykes L R. 1999. Evolving towards a critical point: A review of accelerating seismic moment/energy release prior to large and great earthquakes[J].PureApplGeophys， 155（2/3/4）: 279--305.

Main I G. 1995. Earthquakes as critical phenomena: Implications for probabilistic seismic hazard analysis[J].BullSeismolSocAm， 85（5）: 1299--1308.

Sornette D， Sammis C G. 1995. Complex critical exponents from renormalization group theory of earthquakes: Implications for earthquake predictions[J].JPhysIFrance， 5（5）: 607--619.

Sykes L R， Jaumé S C. 1990. Seismic activity on neighbouring faults as a long-term precursor to large earthquakes in the San Francisco Bay area[J].Nature， 348（6302）: 595--599.

Varnes D J. 1989. Predicting earthquakes by analyzing accelerating precursory seismic activity[J].PureApplGeophys， 130（4）: 661--686.

Wang J C， Shieh C F. 2004. Investigation of seismicity in central Taiwan using the accelerating seismic energy release model[J].TerrAtmosOceaSci， 15（1）: 1--13.

Characteristics of strain release before moderate-strong earthquakes in Yunnan region

（EarthquakeAdministrationofYunnanProvince，Kunming650224，China）

Referring to the earthquake catalogues produced by the Yunnan Regional Seismic Network， and setting the seismic strain energy as a scale of the seismic energy release， this paper conducts a nonlinear simulation for the precursory earthquake-sequences based on the accelerating strain release model. In the period from 1966 to 2013， 115 earthquakes withMS≥5.0 occurred in Yunnan region. Among them， 79 events are characterized by accelerating strain release， accounting for 69%. And 28 events are featured as decelerating strain release， accounting for 24%. The strain releases of the rest eight events accounting for 7% fail to show the features of acceleration or deceleration due to the less seismic data. As to the precursory earthquake sequences whose main shocks belong to the single-shock type， the ones whose earthquake strain releases are accelerating， or the ones lacking seismic data， are far more than the ones whose strain releases are accelerating. As to the precursory earthquake sequences whose main shocks belong to the strike-slip type， the ones whose earthquake strain releases are accelerating are 15% more than the ones whose main shocks belong to the normal-fault type， or 15% more than the thrust-fault type ones. The searching radius has an inverse relation with the duration of the precursory earthquake sequence. The simulated results for the precursory earthquake-sequences indicate that the error of the main shock’s magnitude is ±0.30， and the error of the main shock’s occurrence time is ±0.5 year.

accelerating strain release; power exponent; mid-short term prediction; Yunnan region

10.11939/jass.2015.03.002.

云南省重点项目 （2014JCYB04）资助.

2014-07-14收到初稿， 2014-11-05决定采用修改稿.

e-mail: qxd13@163.com

10.11939/jass.2015.03.002

P315.72+7

A

钱晓东, 李琼, 洪敏. 2015. 云南地区中强地震前应变释放特征. 地震学报, 37（3）: 386--401.

Qian X D, Li Q, Hong M. 2015. Characteristics of strain release before moderate-strong earthquakes in Yunnan region.ActaSeismologicaSinica, 37（3）: 386--401. doi:10.11939/jass.2015.03.002.