城市工业的结构调整与空间分布变化耦合度评价——以武汉市为例<br/>

城市工业的结构调整与空间分布变化耦合度评价——以武汉市为例

2015-03-20郑文升蒋华雄曾菊新朱丽霞王晓芳

地域研究与开发 2015年2期

郑文升，蒋华雄，曾菊新，朱丽霞，王晓芳

(1.华中师范大学 a.地理过程分析与模拟湖北省重点实验室，b.武汉城市圈研究院武汉430079;2.北京大学城市规划与设计学院，广东深圳518055)

0 引言

经济发展在很大程度上来源于产业结构的调整［1］，产业结构调整是生产要素在各行业和空间上的有效组合。为此，衡量一个地区产业结构对了解该地区的经济发展作用很大。主流经济学在强调产业结构变动时，基本是根据产业在国民经济总值中所占比例进行计量研究［2-4］，也有经济学家提出用转移-份额法［5］、马尔科夫链［6］等模型来描述产业内部结构的变化情况;产业的空间结构调整深刻影响着生产要素规模效应和集聚经济的发挥，有学者采用区位因子模型［7］、专业化指数［8］、集中指数［9］等模型探讨产业空间区位选择，以期更科学地研究产业空间的最优分布问题。

实际上，产业结构调整和产业空间分布变化是两个相互独立又相互影响的系统变量，以生产要素的组合与分布为衔接，两者之间存在密切的交互影响。在工业生产中，工业结构变化是不同类型工业发展比例的调整，不同工业的区位要求不同，工业结构的变化必然改变工业空间分布;反之，工业空间分布的变化会改变一定空间范围内工业生产的供需结构与集聚环境，从而影响到相关产业行业的发展，进而影响工业结构调整。这种交互关系可以用耦合来描述，耦合是从物理学引入的概念，是指两个或两个以上的系统或运动形式通过各种相互作用而彼此影响的现象。在实践中，如果工业结构调整能够带来工业空间分布的及时优化，而工业空间分布的变化又能够对工业结构调整发挥充分的支撑引导作用，使生产要素的组合利用最优化、集聚效应最显著，则二者之间就能实现较强耦合，反之，则说明耦合程度较弱。在理论认识中，如何测度二者的耦合程度是研究难点。对工业结构调整的评价可以通过各行业占工业总产值比例的变化程度来反映，但是对工业空间分布变化则不容易进行评价。本研究提出，对工业空间分布变化的评价关键是看各空间单元内生产要素是否得到合理组合与充分利用，即工业空间分布相对生产要素的均衡性，以及是否在各空间单元实现了合理集聚，即工业空间分布相对生产要素的集中性。

以武汉市为例，采用结构调整系数评价工业结构调整度，并引入地理联系系数(coefficient of geographic association)和地理集中指数(index of geographic concentration)分别考察工业空间分布相对生产要素的均衡性和集中性，建立工业结构调整系数和工业空间分布变化评价指标之间的耦合模型，分析两者之间的耦合强度和耦合协调度，划分耦合关系所处阶段。

1 耦合度评价模型

1.1 结构调整系数

工业结构调整反映了各行业所占工业总产值比例的变化情况。采用结构调整系数来综合描述某一时段各行业占工业总产值比例的变化程度，计算公式为:

式中:R表示时期2与时期1的工业结构调整系数，取值范围为0到1，取值越大，表示工业结构波动越大，反之亦然;wj，1，wj，2分别表示时期 1 与时期 2 行业 j的产值占整个工业产值的比例，由于前后两期产值比例变化有正负，取绝对值加总除2就可以消除正负影响，反映整体结构变动情况。

1.2 地理联系系数

地理联系系数主要反映两个地理要素在空间中的吻合程度，间接测度某要素空间分布的均衡性［23］。系数取值范围在0到100之间，值倾向于0表示两个地理要素在空间的分布偏向于分散的非均衡状态，若值越趋近于100表示两个地理要素在空间中的分布越趋于一致，处于相对均衡的状态。从经济学上评价工业空间分布变化的参照物应是生产要素的分布，以判断其对生产要素的利用状况。在柯布-道格拉斯生产函数中，影响工业生产的主要因素可以简化为劳动力与资本，资本可以视为工业生产剩余的再投入。在简化分析框架下，可以将劳动力作为最基本的生产要素［24］，而人口存量与劳动力供给存在正相关关系，因此，可以使用人口数据替代劳动力数据(在一个超大城市内各城区的劳动适龄人口比例不会有太大差距，这种替代并不会显著影响分析结果)。选择规模以上工业企业总产值和人口两个地理要素进行分析，建立地理联系系数公式如下:

式中:I1表示研究区域地理联系系数值;n表示该区域共有n个次级区域;Gi表示某个次级区域的规模以上企业工业总产值表示某个次级区域的规模以上企业工业总产值占全区的比例;Pi表示某个次级区域的人口数量表示某个次级区域的人口占全区的比重。

1.3 地理集中系数

对工业空间分布的研究，还需判断其相对于生产要素的集聚分布状况。基于地理联系系数的分析，同样使用人口作为简化分析下最基本的生产要素。使用地理集中指数能够反映工业生产在空间上的集中程度，同时还可以进一步考察工业在具体哪些次级区域分布集中，该指数表示某个地理要素占全区一半的各地区人口数量在总人口中的比例。指数值的范围在0到100之间，值倾向于0表示该地理要素在空间分布中处于较为分散状态，值倾向于100表示该地理要素在空间分布中趋于集聚状态。选择规模以上工业企业总产值和各区人口来衡量某地区工业地理集中程度，计算公式如下:

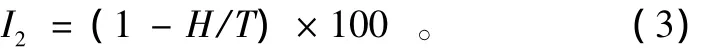
式中:I2表示地理集中指数;H表示当各地区规模以上工业企业总产值占到全区一半所集中的人口数量;T表示全区的总人口数量。

当前，我国正处在由大向强的关键阶段，随着经济总量、综合实力不断上升，各种风险挑战也在增多。人武部应协调宣传部门，搞好传统宣传模式与现代传媒的“无缝衔接”，做好全民国防普及教育。尤其是要抓住高校新生入学军训时机，开展形式多样的国防教育活动，提高青年学生热爱国防、献身国防的自觉性和主动性。

1.4 耦合模型

1.4.1 耦合强度模型。采用物理学中描述两个或两个以上系统相互影响程度的容量耦合模型来分析工业结构调整与工业空间分布变动之间的耦合强度。公式为:

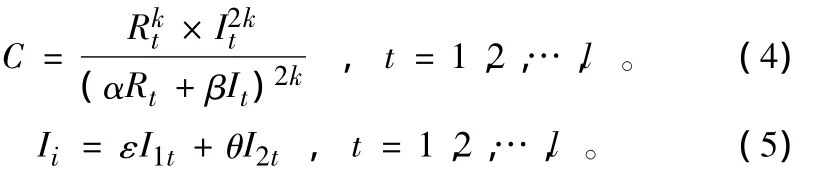
式中:C表示工业结构调整与工业空间分布变化(工业地理联系系数、工业地理集中系数)的耦合强度，且C∈(0，1)，当C倾向于0时，耦合强度极小，系统或系统内部要素之间将趋于非相关无序状态，当C趋于1时，系统或内部要素之间将趋于有序高度相关状态;α和β，ε和θ为待定系数，且α+β=1，ε+θ=1。由于工业结构调整与产业的空间分布变化相互独立又相互影响，取α=β=0.5，ε = θ=0.5;εI1t+ θI2t表示工业空间分布变化的综合系数;k值为调节系数，且k∈(2，8)，k取中值5;t表示以1995年为基年的年份序数。理想情况应是工业结构调整程度与工业空间分布变动呈有序相关，但根据耦合强度C的取值，可以将两者的耦合强度划分为3个阶段:0≤C≤0.3为低强度耦合阶段;0.3＜C≤0.5为中强度耦合阶段;0.5＜C≤1为高强度耦合阶段。

1.4.2 耦合协调度模型。C能够很好反映工业结构调整与工业空间分布变化的耦合强度及时序关系。然而，耦合强度在进行多个区域对比研究时却很难反映出两个子系统对系统的整体“功效”和“协同”效应［25］，因而构造工业结构调整与工业空间分布变化系数的耦合协调度模型，判断地区工业结构调整与工业空间集聚分散的交互耦合协调程度，公式为:

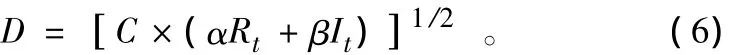
式中:D为耦合协调度，且D∈(0，1)。根据耦合协调度D的取值范围，可以将工业结构调整与工业空间均衡性划分为4个阶段:0≤D≤0.3时为低水平耦合，即工业结构调整程度相对较低，工业空间分布过度分散，传统工业占据主导且不能在空间上发挥集聚效益，工业发展缓慢;0.3＜D≤0.55时为拮抗阶段，工业结构发生较大变动，改变原有传统的工业模式，工业空间聚集明显，集聚经济效益得以发挥，但此时工业结构的优化并不能与工业空间调整取得一致，二者对系统整体的推动作用较差;0.55＜D≤0.8时为磨合阶段，结构的调整和工业空间集聚所取得的效益趋于一致，能够形成促进经济发展的合力;0.8＜D≤1为高水平耦合阶段，工业结构的调整和工业生产空间分布产生了叠加双重经济效益，既取得了结构优化效益，又取得了工业空间效益，但是两者的关系在内外力作用下仍面临退化风险。

1.4.3 耦合阶段划分。前文C值反映了两子系统之间的作用强弱，而两系统间协同程度则是系统优化的过程，根据耦合交互协调度D值［26］，在长时间尺度上可划分为低水平协调、拮抗、磨合和高水平协调4个耦合阶段(表1)。

表1 工业结构调整和工业空间分布的耦合协调度划分Tab.1 Divided stage of coupling coordination degree between industry-structure change and space distribution

2 实证研究区域和数据说明

以武汉市作为研究对象，以武汉市13个区作为基本研究单元(能够获取数据的最小单元)，其中心城区分别为江岸区、江汉区、硚口区、汉阳区、武昌区、青山区、洪山区，郊区分别为东西湖区、汉南区、蔡甸区、江夏区、黄陂区、新洲区，这种以行政区为单位的划分也和武汉市实际的中心城区和郊区分布一致。研究数据采用1996—2014年《武汉市统计年鉴》的分区规模以上工业企业产值数据、分行业规模以上工业企业产值数据及分区人口数据。1995—2013年是武汉市改革开放以来工业结构调整最为显著的时期，传统的钢铁、造船、重机、纺织等产业地位逐渐下降，新兴的汽车、光电、化工、医药等产业迅速壮大，也是武汉的开发区建设、老工业区改造、“退二进三”等工业布局调整最为突出的时期，能够比较典型地反映20世纪90年代以来我国老工业城市工业结构调整与工业空间分布变化的相互关系。

3 耦合度评价

3.1 武汉市工业结构调整系数

武汉市作为全国重要的工业中心，近十几年来，形成了以钢铁、汽车、光电子、化工等产业为主导的工业体系。1995年，武汉市分区规模以上工业企业产值总和不到150亿元，到了2013年，分区规模以上工业企业产值超过6 000亿元，期间平均增长率为25.11%，规模以上企业的平均产出超过3亿元，企业的效益和规模都得到了巨大的提升。同时，武汉市工业结构发生了巨大变化，1995年冶金行业占武汉市工业产值的比例最大，达到了38.20%，产业层次相对较低;到2013年，通信电子、交通电气、医药等高端行业占工业总值比例超过了50%，产业结构得到明显提升。

采用武汉市规模以上企业工业产值，计算武汉市工业结构的同比结构调整系数和累计结构调整系数(以1995年为基期)，可以发现从1995年开始武汉市工业结构调整显著，在各阶段呈现不同特征。同比结构调整系数显示，武汉市工业结构1998—2002年经历了剧烈变化，系数值从0.08急剧上升到1999年的0.28，累计上升0.20，随后又突降到2002年的0.06，之后进入到平稳波动的发展阶段;2007年，系数值达到最低，为0.05，随后波动上升到2010年的一个小高峰0.16，之后工业结构呈现波动变化，达到2013年的0.14。从累计结构调整系数来看，武汉市工业结构调整程度在逐渐加大，系数值由1995年的0.12上升到2000年的0.30，之后短暂地下降到2004年的0.22，之后又波动上升到2011年的最大值0.40，随后又大幅波动上升，达到2013年的0.77;分析表明，武汉市各工业行业产值占总产值的比例较初期发生了较大的变动，间接反映了市场和政策对武汉市工业所作出的调整(图1)。

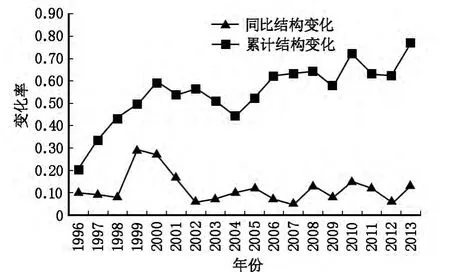
图1 1996—2013年武汉市工业结构变化Fig.1 The change of industry-structure in Wuhan City during 1996—2013

3.2 武汉市工业分布地理联系系数

武汉市工业总体发展较快，但是空间分布波动较大。利用公式(2)计算武汉市规模以上工业产值和人口的地理联系系数表明，武汉市工业空间分布长期呈现非均衡性，即规模以上工业企业产值在各区的比例和其相应区域的人口比例差异较大，联系系数在2005年之前一直低于40，间接反映出了武汉市就业空间和居住空间相分离的态势。2005年后这种态势有所缓和，武汉市工业空间分布的均衡性得到了显著地提高，地理联系系数由2005年的21上升到2009年的49，然后缓慢波动后又急剧上升到2013年的65。这种工业空间分布均衡性的反复波动，不仅是其对工业结构调整所做出的反应，也是其自身寻求空间区位最优的过程体现(图2)。

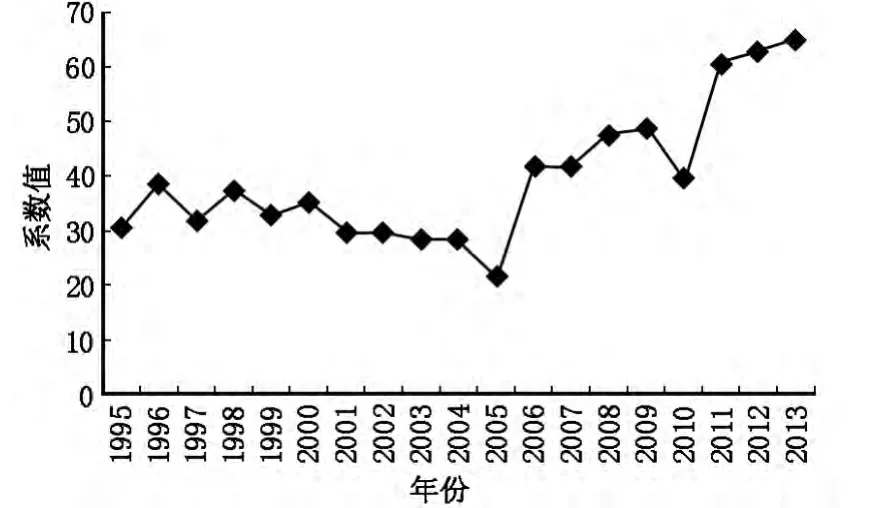
图2 1995—2013年武汉市工业地理联系系数值Fig.2 Coefficient of geographic association of industry section in Wuhan City during 1995—2013

3.3 武汉市工业分布地理集中指数

为了进一步弄清楚工业空间非均衡性的空间表现形式，利用公式(3)分析武汉市工业具体在哪几个区集聚，在这些区的集中程度如何。采用武汉市1995，2000，2005，2013年规模以上企业的工业产值(简称工业产值)数据计算地理集中指数，各个指数代表了武汉市工业在这些集聚区的集中程度。

1995年武汉市东西湖区、黄陂区、江夏区和新洲区28.3%的工业产值占到了整个武汉市的一半，该时期武汉市的工业相对集中在外围的郊区，集中指数为70。到2000年，蔡甸区、洪山区、汉南区和东西湖区68.5%的工业产值占到武汉市的一半，其中江夏区、黄陂区和新洲区被蔡甸区、洪山区和汉南区代替，东西湖区排名后退，工业发展在郊区集聚的趋势得到增强，集中指数上升到82;值得注意的是，洪山区成为第一个进入累计工业产值占武汉50%的城区。到2005年，武汉市工业发展呈现2个趋势:①工业空间分布相对分散，武昌区、洪山区、东西湖区、青山区和汉阳区5个区30.9%的工业产值占到武汉市的一半，地理集中指数下降到66;② 相对于2000年工业产值占武汉50%的区域，2005年城区个数共有4个，郊区只有东西湖区1个。到了2013年，武汉市工业产值向城区集中的趋势更加明显，青山区、汉阳区和洪山区3个区的工业产值比例已经超过了武汉市50%，集中指数高达76。可以看出，从1995年以来，武汉市工业发展经历了由郊区逐步向城区转移的过程，这种转移反映了城区良好的区位、高素质的劳动力等要素对工业发展的推动。值得说明的是，2013年以来，占武汉市工业产值4～8位的都是郊区，可以预见，随着未来武汉市对郊区和城区工业发展新的功能定位，工业布局将在空间上进行新优化调整，工业定会在全区得到协调发展(图3)。

3.4 耦合强度与耦合协调度

利用公式(4)和(6)计算耦合强度C值和耦合协调度D值表明，1995年以来，武汉市工业结构调整和工业空间分布变化的作用强度和交互协调关系的变化趋势基本一致，即两系统要素作用较强的时候，交互协调性较好，当两系统要素作用较弱的时候，两者交互协调度较差。

在15个年份中，武汉市的耦合协调类型没有出现较高水平耦合阶段，大部分时期处于拮抗阶段。如1996—1998年武汉市工业结构调整和工业空间分布变化的作用强度适中，部分工业在收缩扩张过程中努力寻找空间布局上的最优，但协调性一般;1999—2000年耦合协调度处于较高水平，两系统要素的相互作用较强，工业结构的大力调整推动了工业在空间布局的变化，这与当时武汉市国企改革、进行大规模的产业结构调整和空间分布变化有关;同时，低水平耦合的前后阶段通常是工业结构调整和工业空间分布变化作用较强、协调较好的时期。如武汉市工业结构和工业空间分布变化的C值和D值在2002和2007年都比较低，但2002年前后，武汉市工业结构调整和工业空间分布变化都处于中等强度的拮抗或高协调的磨合阶段，2007年前后处于中等强度的拮抗阶段。2010年之后，工业结构和工业空间分布变化的C值和D值呈现大幅下降趋势，两个值分别下降到2012年的0.22和0.29，两者相互作用强度及协调性都较低，而此时工业增长率较为缓慢。2013年虽然C值和D值上升到0.55和0.48，但工业短期调整较慢，增长率较低。工业结构和工业空间的耦合关系与一个地区工业发展的规律联系紧密，当一个地区工业结构和空间布局经过前一阶段的巨大波动，必然需要一段时间进行消化吸收，完成工业结构的自我优化和工业空间布局的自我调整，从而引起下一个阶段的工业的快速增长。

当一个地区工业结构调整和工业空间分布变化的耦合强度和耦合协调度较大时，工业结构调整和工业空间分布变化相互作用较强，协调较好，共同推动工业的发展。通过比较武汉市工业耦合强度C值、耦合协调度D值和武汉市工业增长速度发现，随着两个值不断变大，工业增长的速度明显加快，当两个值较小时，工业增长的速度也相对较慢。这也直接体现了表1所反映的工业耦合协调的阶段特征，即当工业结构变动与空间分布变化作用较强、协调性较高时，工业发展的集聚经济和结构效益得到双重发挥，共同推动经济的发展(图4)。

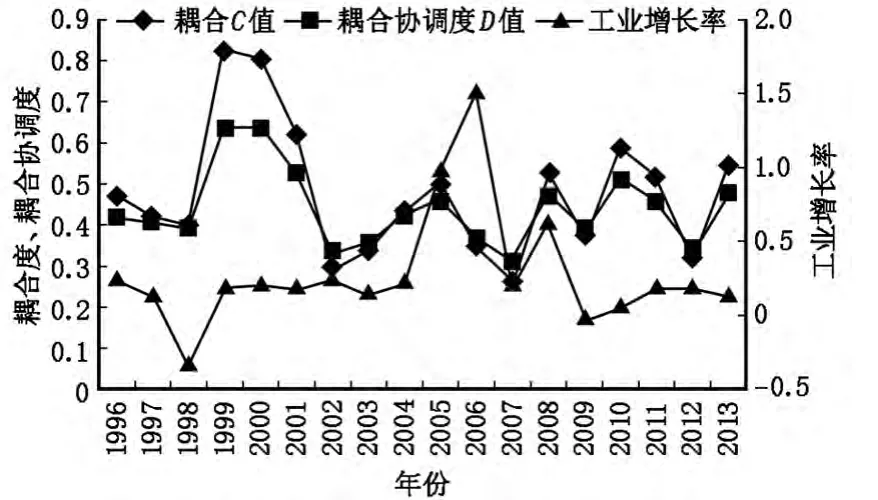
图4 1996—2013年武汉市工业耦合协调值及增长情况Fig.4 Coupling coordination degree and industrial growth in Wuhan City during 1996—2013

近十几年武汉市工业结构调整和工业空间分布变化相互作用推动工业增长，呈现反复波动、交替变化的过程，反映了地区政策所发挥的阶段性作用。如武汉市政府在2002年建立区级经济开发区16个、镇级工业园22个，加大对电子信息、化工、汽车等行业的投资，推动工业结构发生较大变化，工业空间摩擦较为剧烈;经过一段稳定期后，2006年后随着“十一五”规划的实施，武汉市加强了东湖、武汉和吴家山三大经济技术开发区和6个远郊工业集聚区的建设，大力发展信息技术、生物和新能源等高新技术产业，工业结构和工业空间分布又经历了新一轮的剧变。这说明，一个地区在进行工业结构的优化过程中，需要工业在空间布局上做出积极反应;同样，工业在进行空间区位最优化时也需要工业结构做出积极的调整，这样才能形成集聚和结构的双重效益，推动地区经济的发展。

4 结论与讨论

采用结构调整系数定量描述工业结构调整度，引入地理联系系数和地理集中指数考察工业空间分布变化，同时，通过建立耦合关系模型，结合武汉市的工业结构调整和工业空间分布变化，探讨两系统要素之间的交互耦合协调关系。与耦合关系模型在解释两个系统要素的一般特征一样，工业结构调整和工业空间分布变化在时序上存在有序与无序、协调与不协调两种关系，根据D值可以划分为低水平协调、拮抗、磨合和高水平协调四个耦合协调阶段。

1)对武汉市工业结构调整、工业空间布局的变化和工业集中度进行分析表明:武汉市各工业行业产值占总产值的比例较初期发生了较大的变动，工业结构发生了较大变化;工业长期呈现非均衡性分布，工业发展经历了由郊区逐步向城区转移的过程;工业耦合协调类型大部分时期处于拮抗阶段，工业增长和工业结构调整与工业空间分布变化之间的作用强度、协调关系紧密相连。

2)工业结构变动和工业空间分布变化作用强弱与两系统要素的协调性高低联系较为密切。当C值很高时，通常情况下存在较高的D值，即朝着结构最优的工业变化很大程度上引起工业追求空间分布的最优;反之，工业结构调整和工业空间分布变动在协调性较好时，两系统要素的作用强度相对较高。武汉市工业结构调整和工业空间分布变动耦合作用较强时，二者的交互协调性也较高。

3)耦合强度C值和耦合交互协调度D值的高低影响工业总体的发展速度。若武汉市工业结构变动和工业空间分布变化的耦合C值和耦合交互协调D值较低时，工业增长速度相对较慢，而两个值较高时，工业增长相对较快。这说明，当某一地区在某时段工业结构变动和工业空间变化作用强度较大，协调性较好的时候，形成了一股合力，不仅会促进工业的发展，而且会推动工业本身结构的完善和空间的优化。

［1］金碚，吕铁，邓洲.中国工业结构转型升级:进展、问题与趋势［J］.中国工业经济，2011(2):5-15.

［2］罗斯托.从起飞进入持续增长的经济学［M］.贺力平，译.成都:四川人民出版社，1988.

［3］库兹涅茨.各国的经济增长［M］.2版，常勋，译.北京:商务印书馆，1999.

［4］钱纳里，塞尔昆.发展的格局(1950—1970)［M］.李小青，译.北京:中国财政经济出版社，1989.

［5］ Knudsen D C.Shift-share Analysis:Further Examination of Models for the Description of Economic Change［J］.Socio-Economic Planning Sciences，2000，34(3):177-198.

［6］ Chin S，Greenberg E.Markov Chain Monte Carlo Simulation Methods in Econometrics［J］.Econometric Theory，1996，12(3):409-431.

［7］李小建，李国平，曾刚，等.经济地理学［M］.2版.北京:高等教育出版社，2006.

［8］ Leigh R.The Use of Location Quotients in Urban Economic Base Studies［J］.Land Economics，1970，46(2):202-205.

［9］ Schmalensee R.Using the H-Index of Concentration with Published Data［J］.The Review of Economics and Statistics，1977，59(2):186-193.

［10］李娜，孙才志，范斐.辽宁沿海经济带城市化与水资源耦合关系分析［J］.地域研究与开发，2010，29(4):47-51.

［11］刘耀彬，宋学锋.城市化与生态环境耦合模式及判别［J］.地理科学，2005，25(4):408-414.

［12］吴玉鸣，柏玲.广西城市化与环境系统的耦合协调测度与互动分析［J］.地理科学，2011，31(12):1474-1479.

［13］刘耀彬，李仁东，宋学锋.中国区域城市化与生态环境耦合的关联分析［J］.地理学报，2005，60(2):237-247.

［14］赵雪雁，周健，王录仓.黑河流域产业结构与生态环境耦合关系辨识［J］.中国人口·资源与环境，2005，15(4):69-73.

［15］李边疆，王万茂.区域土地利用与生态环境耦合关系的系统分析［J］.干旱区地理，2008，31(1):142-148.

［16］刘浩，张毅，郑文升.城市土地集约利用与区域城市化的时空耦合协调发展评价——以环渤海地区城市为例［J］.地理研究，2011，30(10):1806-1817.

［17］张燕，吴玉鸣.中国区域工业化与城市化的时空耦合协调机制分析［J］.城市发展研究，2006，13(6):46-51.