朗之万方程在布朗运动数值模拟中的时间尺度分析

郭颖旦，丁望峰，杨建宋

(杭州师范大学理学院，浙江 杭州310036)

0 引 言

布朗运动是指悬浮于气体或液体中的微小颗粒受到周围分子热运动产生的撞击而做永不停息无规则运动的现象.1827年，植物学家罗伯特·布朗首次对布朗运动进行了系统的描述，但直到1905年才由爱因斯坦根据统计理论给出定量的解释［1］. 与此同时，M. von Smoluchowski 也独立发展出一套理论来解释布朗运动，并给出了相似的结果［2］.1908年，Paul Langevin 采用了一种更为直观的方法来描述布朗运动，即在牛顿第二定律的方程中引入随机力作用项，即著名的“朗之万方程”［3］:

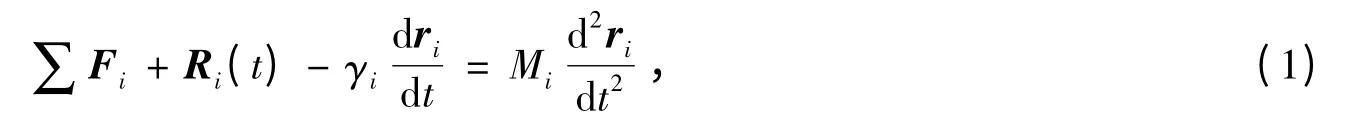
其中Mi为布朗颗粒质量，ri为位置矢量.等式左边第一项是布朗颗粒受到的其它颗粒或外场的作用力之和;第二项把周围流体分子对布朗颗粒撞击作用等效表示为一个随机作用力;第三项是微粒在流体中运动受到的黏滞阻力，其中γi是颗粒i 的阻力系数，对于半径为a 的球形颗粒，按Stokes 公式计算其摩擦系数γ 为

其中η 是液体在一定温度下的黏度.

根据随机耗散理论，随机作用力Ri(t)与摩擦系数满足如下关系

其中kB是玻尔兹曼常数，T 是环境温度.

在实际模拟中，往往假定随机作用力在不同时刻是不相关的，即式(4)可采用如下式

该等式把布朗粒子受到的随机热扰动与体系温度及摩擦系数关联起来.

当液体的黏滞阻力很大时，布朗颗粒的质量可以忽略，其运动轨迹类似于无质量的粒子.这时式(1)等式右边可近似等于零，即

该等式也被称为位置朗之万方程，是朗之万方程的“过阻尼”形式［4］.基于式(6)进行的模拟称为布朗动力学(Brownian Dynamics，BD)模拟，而通过式(1)进行的模拟称为朗之万动力学(Langevin Dynamics，LD)模拟.

分子动力学一般以原子为最小研究单元，在模拟过程中需考虑原子与原子之间的相互作用力.而在布朗运动的模拟过程中，分子水平的作用力被简化成一项随机作用力，解决了分子动力学直接以牛顿运动方程追踪系统中所有布朗粒子与流体分子轨迹的困境，因而被广泛应用于胶体科学和生物物理领域［5］. 然而这种简化是基于大量流体分子撞击前提下的，即需要一定的时间以保证足够次数的撞击发生，这也是布朗颗粒动量发生明显变化所需要的弛豫时间，定义为

最近实验研究显示，在极小的时间尺度下，布朗颗粒受到流体分子的等效作用并非是完全随机的白噪声［6］.计算机数值化模拟实际上是把连续的过程分割成时间间隔为Δt 的一系列状态点，通过计算从t 时刻到t+Δt 时刻状态点的演化来模拟真实的物理过程.当Δt≪τp时，把流体分子的作用等效成随机作用项Ri(t)将不能反映真实物理过程. 而在实际模拟过程中，Δt 的取值往往由颗粒之间的势能曲面形貌所决定，所以讨论不同Δt 的取值对模拟结果的影响有着重要意义.

本文对单个布朗颗粒的运动轨迹分在不同时间步长Δt 下分别进行了LD 模拟和BD 模拟，并对结果做出比较分析.根据爱因斯坦理论，通过测量布朗运动的轨迹可以计算出阿伏加德罗常数值，我们以此为依据对LD 和BD 模拟所得轨迹的物理真实性进行验证.

1 朗之万方程的数值化

这里记位矢ri的三维坐标为(x1，x2，x3)，三维速度矢量(v1，v2，v3)，则在根据式(1)，xα(α=1，2，3)方向上粒子i 从时间t 到t+Δt 基于Euler 算法的演化方程为［7］

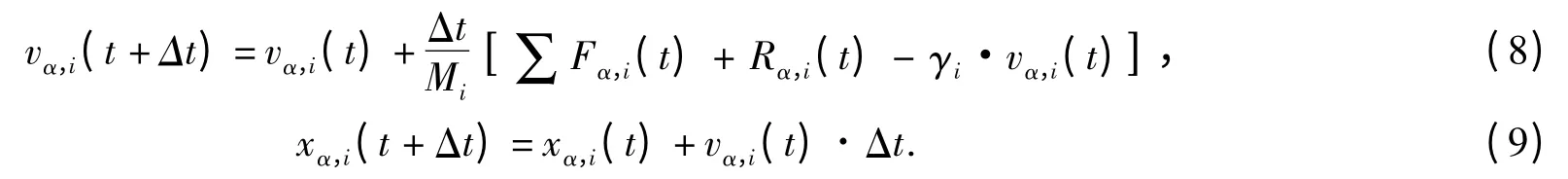
相应的位置朗之万方程可以写成

从上式可以看出，位置朗之万方程中并不出现速度，粒子下一步的走向完全取决于粒子此刻受到的作用力(当Δt 足够小时可看成恒力)和热扰动产生的随机作用力.

为了满足式(3)和(4)要求，这里的随机作用力Rα，i(t)可以取一个期望值为0、标准差为的高斯分布，记为

如果再记布朗扩散系数D 为

则式(9)可写成

通过上式不难发现，在不考虑颗粒间相互作用和外场影响时，位移的平均平方差满足布朗运动理论的推导结果

相对而言，从式(7 -8)并不能直接得到位移的平方差表达式，我们将在下面具体的模拟中做进一步分析.

在下面的结果与讨论中，LD 模拟与BD 模拟将分别基于式(8 -9)和式(10)来实现.

2 结果与讨论

我们选取悬浮在室温纯水中的球形SiO2颗粒作为研究对象，模拟其在二维平面内的布朗运动轨迹，具体参数见表1.

2.1 不同模拟时间步长对比

为了便于比较，每次模拟均采用一串相同的“伪随机数”，即颗粒在t 时刻受到相同的随机作用力. 如果模拟的参数相同，则布朗颗粒的“随机”运动轨迹完全相同.

计算过程中积分的时间步长选择一般由颗粒之间的作用势所决定，越“陡峭”的势能曲面需要越小的时间步长.由于这里只考虑单个布朗颗粒的运动，不涉及颗粒之间的作用力，因而时间步长可以在一个较大的范围内选择.图1 是在保证其他参量相同的前提下，使用不同的模拟时间步长Δt 分别进行LD 和BD 模拟得到的单颗粒布朗运动轨迹图，每条轨迹代表模拟中最初250 步随机行走.

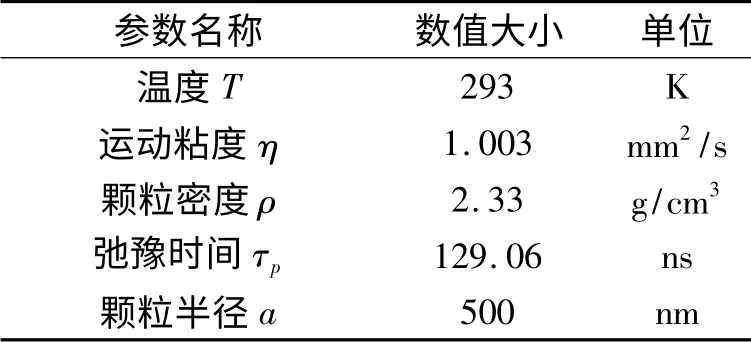
表1 SiO2 颗粒在水中作布朗运动的模拟参数Tab. 1 Parameters for the Brownian simulation of SiO2 spheres in water

由图1 可见，随着时间步长Δt 的增大，模拟的总时间增大，因而行走的空间距离也相应增大.不同的是，BD 轨迹除了空间尺度的变化外，轨迹形状完全相同.这从式(10)中也可以看出，时间步长Δt 仅线性地改变了行走的步长.而对于LD 模拟而言，Δt 越小，颗粒本身的惯性质量越突显，模拟轨迹就越接近于宏观物体的实际运动轨迹，是一条较为平滑的曲线.随着Δt 的增大，像所有的分子动力学模拟一样，每步行走的步长增加，LD 的轨迹变得越来越跳跃，并最终导致模拟数据溢出，如图1(A)最下面一幅图所示. 对更多的Δt 值进行比较，我们发现当Δt 接近于颗粒的弛豫时间τp时，BD 和LD 轨迹最相似.

BD 是LD 的简化，进行BD 模拟的前提条件是物理过程必须满足布朗运动的特征，只要条件满足，模拟的时间步长可由其它因素决定.而LD 模拟的Δt 取值受实际物理条件制约，存在上限值.这就会出现这样的矛盾:随机作用项Ri(t)引入的条件是时间步长Δt 足够大(Δt ≫τp)，使流体分子的作用可以简化为一个随机作用力;而对于普通的布朗颗粒，动力学模拟中势能曲面要求的时间步长远小于其弛豫时间τp.所以在实际计算中，Δt 的取值往往比弛豫时间小很多.那么这样的处理方式是否科学，下面通过对输出轨迹的定量计算进行讨论.

2.2 布朗运动轨迹的定量分析

1905年，爱因斯坦首次发表了布朗运动的定量分析理论，在文章的最后，他给出了验证理论正确性的方法，即

其中NA是阿伏加德罗常数，Δt 是运动轨迹上邻近两个记录点的时间间隔，R 是气体常数，T 是实验温度，η 是实验温度下液体的黏度，a 是球形微粒的半径.通过测量轨迹图上颗粒在x 方向上位移的平均平方值就可以计算出阿伏加德罗常数的实验测量值.这里用此公式对模拟轨迹图进行定量分析，并用计算所得的NA值与标准值相比较来对模拟的物理真实性进行评判.

这里所用的“伪随机数列”以每次运行时计算机时间为种子产生，从而保证了轨迹的随机性.对于每个时间步长Δt，我们共计算了n = 105步随机行走的平均位移平方＜λx2 ＞，并得到了如图2 所示的计算结果. 需要注意的是，当Δt ＞300 ns 时，LD 模拟数据已经溢出.所以对于此时间步长范围内的LD 模拟，采用Δt = Δt′ × N的模式，即实际模拟时间步长为较小的Δt′，但间隔N 步输出一次坐标，这样输出轨迹上点之间的时间步长为Δt.例如Δt =1000 ns 时，实际Δt′ =10 ns，N=100.计算表明，只要Δt 的取值不变，不同Δt′和N 的取值对结果几乎没有影响.

从图2 可以看到，BD 轨迹与Δt 无关，由此计算得到的阿伏加德罗常数值非常接近其标准值6.022 ×1023.而LD 模拟在Δt 较小时得到的NA值明显偏大，这是因为在很短的时间内要保证流体分子对布朗颗粒作用的热力学统计性，势必需要更大量的分子，这就表现为NA值偏大.上面提到，布朗颗粒的弛豫时间τp是其受微观分子撞击引起动量变化的特征时间，当时间步长小于该特征时间时，就需要更大量的分子撞击使之产生动量上的变化，即对应更大的阿伏加德罗常数值;当时间步长大于τp时，足够数量的分子撞击符合热力学统计要求，由此可得到正确的NA值.图2 中的LD 曲线的趋势也证实了布朗颗粒的弛豫时间(τp=129.06 ns)是NA取值是否正确的“分水岭”.同时，计算结果也证实了在LD 模拟中，即使时间步长小于弛豫时间，对于长时间的宏观观测而言该模拟也是符合真实物理规律的.

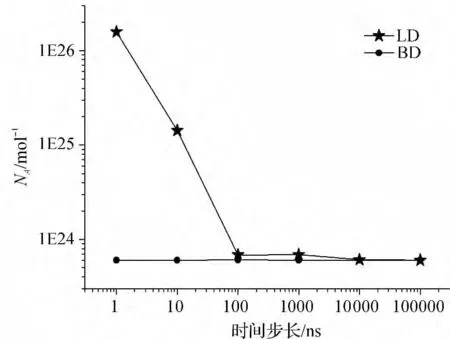
图2 用不同时间步长分别进行LD 和BD 模拟，并对其输出轨迹进行计算得到的阿伏加德罗常数值NAFig. 2 Values of the Avogadro constant calculated from traces of Langevin dynamics and Brownian dynamics simulations performed with different time-steps

3 结 论

本文从朗之万方程出发，分别用朗之万动力学(LD)和布朗动力学(BD)方法对单颗粒的布朗运动进行了数值化模拟，并重点讨论了不同时间步长对模拟结果的影响.LD 是在牛顿动力学的基础上加入了随机作用项以等效流体分子对布朗颗粒的碰撞，必须满足热力学的大数量统计.当时间步长太短时，分子碰撞次数不足以等效成随机作用，所以在较小的时间尺度下，这样的等效是不符合物理事实的;然而在宏观时间尺度下，发现LD 模拟轨迹并不违背物理规律.BD 是对LD 的简化，其成立条件是体系满足布朗运动的所有特征，因而在具体模拟过程中与时间步长无关.

［1］Einstein A. Investigations on the Theory of the Brownian Movement［M］. New York:Dover Pulieation Inc，1956.

［2］Smoluchowski M von. Zur kinetischen Theorie der Brownschen Molekularbewegung und der Suspensionen［J］. Annalen der Physik，1906，326(14):756-780.

［3］Langevin P. Sur la théorie du mouvement brownien［J］. CR Acad Sci Paris，1908，146:530-533.

［4］Coffey W T，Waldron J T，Kalmykov Y P. The Langevin Equation［M］. Singapore:World Scientific，2004.

［5］王子瑜，曹恒光.布朗运动、朗之万方程式、与布朗动力学［J］.物理双月刊，2005，27(3):456-461.

［6］Li T C，Raizen M G. Brownian motion at short time scales［J］. Annalen der Physik，2013，525(4):281-295.

［7］Leach A R.分子模拟的原理和应用［M］.2 版.伦敦:世界图书出版公司，2001.