Two Kinds of Improved Fourth-order Iterative Methods for Solving Nonlinear Equations

WANG Xiaoya，MA Guochun

(1.School of Science，Hangzhou Normal University，Hangzhou 310036，China;2.Tonglu Experimental Junior Middle School，Hangzhou 311501，China)

1 Introduction

In this paper，we consider the following nonlinear equation，

Let x=(x1，x2，…，xn)T∈ℝn，F(x)=(f1(x)，f2(x)，…，fn(x))T∈ℝn，then (1)can be written as F(x)=0，where F:D⊂ℝn→ℝnis continuously differentiable.

By the Taylor expansion，we get

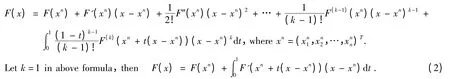
Employing the Left Rectangular integral formula，we obtain

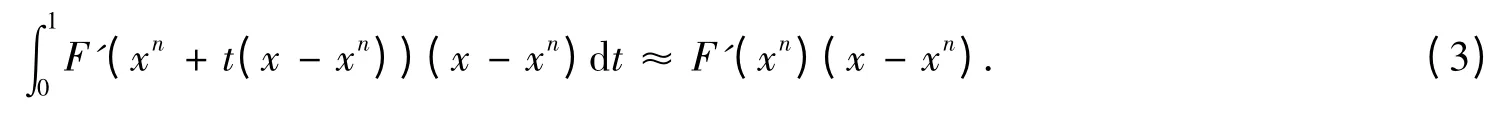
Combining (2)and (3)，we have F′(xn)(x-xn)≈-F(xn).

Hence，there is Newtons iterative formula［1］

which has quadratic convergence［2］.

It is well known that there are plenty of methods，for example，quadrature formulas，Taylor series，decomposition techniques and so on to solve the nonlinear equation(1). Among these methods，the most common of one is Newton′s iterative methods.Because of rapid convergence，people are interested in high-order Newton′s iterations［3］.

In 1967，Šamanskiǐ V. E. put forward the Modified Newton method［4］，he simplified m Newton step to single Newton step:，i=1，2，…，m;n=0，1，2，….

When m=1，it is Newton′s iterative formula;when m=2，it can be changed into

In 2010，(5)was proved to be the third-order of convergence［5］.

Back to (3)，employing different numerical integral formulas，we can obtain a series of improved iterative formulas.

In 2007，based on the Adomian decomposition method［6-7］，M.T.Danvishi and A.Barati obtained two-step iterative formula to solve nonlinear equation(1):

and they proved that it has third-order convergence.

In 2009，Muhammad Aslam Noor and Muhammad Waseem［8］use two-point Newton-cotes formula to approximate (3)，at the meantime，regarding Newton′s iterative formula as first iterative step，they get two kinds of improved two-step iterative formulas as follows to solve nonlinear equation(1):

and they proved they have third-order convergence.

In 2010，employing the Gauss quadrature formula［9］to approximate (3)and combining Newtons iterative formula，Renduan Gao get the Gauss-Newton iterative formulas:

one-point G-N iterative formula:

two-point G-N iterative formula:

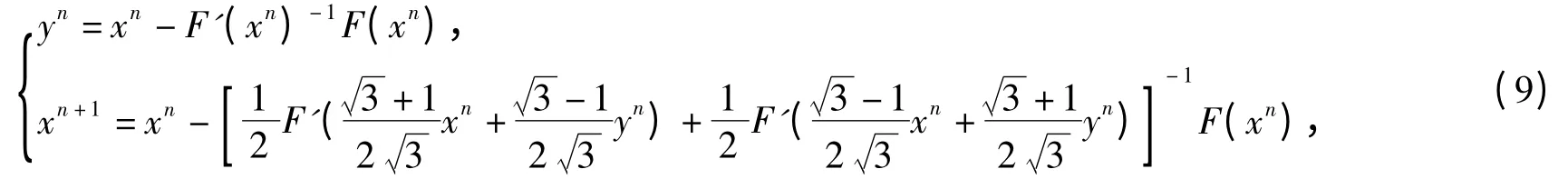
and he proved that they have third-order convergence.

In 2012，Lulu Dai and Jieqing Tan［1］put forward two kinds of iterative methods to solve nonlinear equation(1)which are based on the Adomian decomposition method and Newton-Cotes formula:

the first iterative formula:

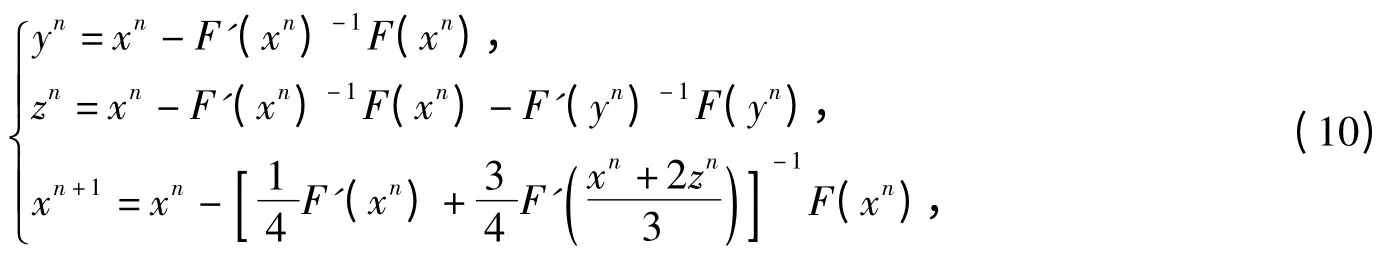
and they proved that it has fourth-order convergence;

the second iterative formula:

and they proved that it has third-order convergence.

Inspired by［1］，based on the previous methods of solving nonlinear equation(1)，we come up with two kinds of improved fourth-order convergence iterative methods，which employ two-point Gauss quadrature formula as the last step of the iteration. On the one hand，both of them are three-step iterative schemes. On the other hand，their convergence speeds are good. Furthermore，we use the Taylor’s expansion to prove our results mainly. Because the difficulty of the proof of three-step iterative schemes，we prove the order of the first two-step first，and then we give the proof of our results.

In the rest of this paper，we give our results firstly and prove the results then. At last，numerical experiments are demonstrated to show the two new iterative schemes comparing with Newton′s iterative method，especially the second iterative scheme have better convergence speed. The convergence speeds of different iterative schemes in each iteration between the approximate solution and exact solution of the equation shows the superiority of the iterative schemes in our paper.

2 Main results

The Trapezoidal integral formula is a mechanical quadrature method，the geometric meaning of it is to use trapezoid area to replace the curved trapezoid area which for the top of y=f(x)approximately.

Employing the Trapezoidal integral formula:

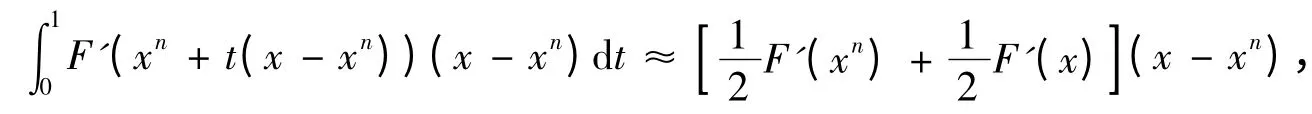
and two-point G-N iterative formula of Renduan Gao［9］，using Newton′s iterative formula as the first iterative step so that we can get an improved three-step iterative scheme to solve nonlinear equation(1).

Theorem 1Assume F:D⊂ℝn→ℝnis third-order differentiable in D，if there exists x*∈D，such that F(x*)=0，then the following iteration

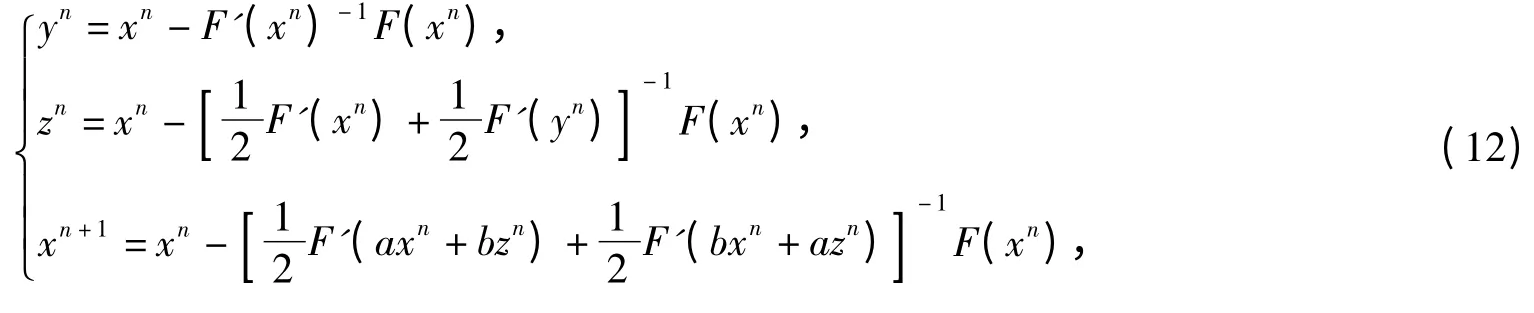
The Adomian decomposition method is a powerful tool to investigate the approximate or even closed-form analytical solutions of nonlinear differential equations.It provides more realistic solutions by solving the nonlinear problem without simplification.The main idea of it is to decompose the equation into several parts appropriately，the solution of equation is decomposed into infinite amount of decomposition，then generated with the equation of the nonlinear terms equivalent polynomial and inverse operator is used by low-order solution components to introduce high-order solution components so as to obtain high-precision approximation solution even the exact solution［10-11］.

Combining the Adomian decomposition method and two-point G-N iterative formula，using Newton′s iterative formula as the first iterative step so that we can get another improved three-step iterative scheme to solve nonlinear equation(1).

Theorem 2Assume F:D⊂ℝn→ℝnis third-order differentiable in D，if there exists x*∈D，such that F(x*)=0，then the following iteration

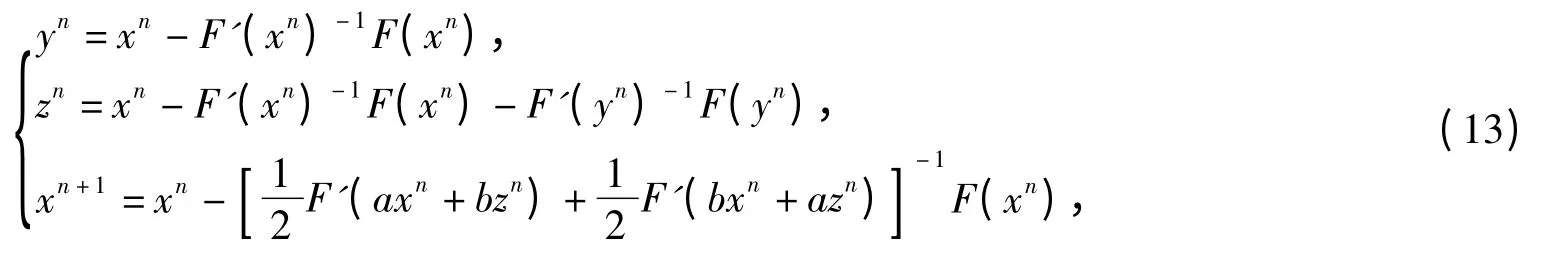
3 Proofs

Lemma 1Assume F(x):D⊂ℝn→ℝnis reversible and nonsingular，if there exist x*∈D，such that F(x*)=0，then

has third-order convergence.

ProofLet

and en=xn-x*，then en+1=en-A-1F(xn)，equivalently，

Using the Taylor formula at point xn(n=0，1，2，…)，we get

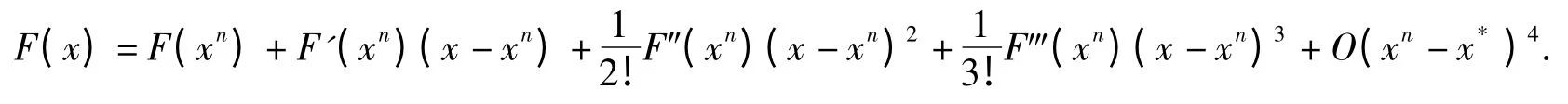
Let x=x*so that

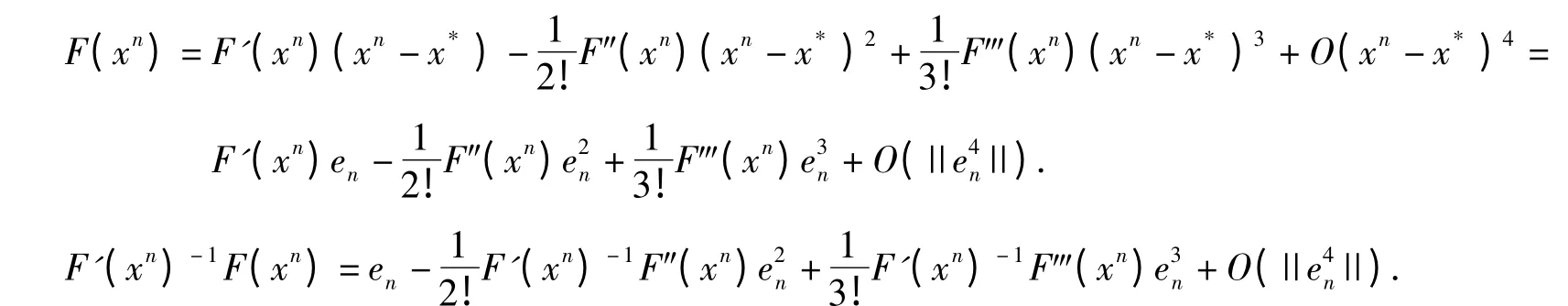
Using the Taylor formula to F′(yn)at point xn，we get

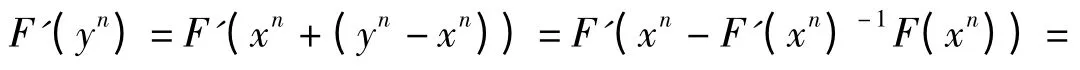
Combining (15)and (17)，we have

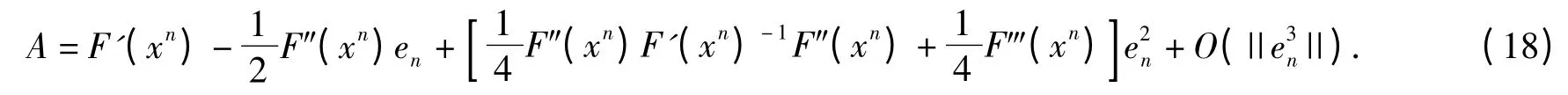
Combining (16)and (18)，we have

which means(14)has third-order convergence.

Proof of Theorem1From Lemma 1，we have the following error formula:

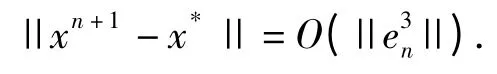
Let

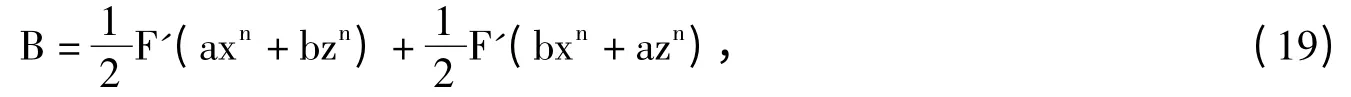
then

equivalently，

Using the Taylor formula to F(xn)，F′(axn+bzn)and F′(bxn+azn)at point x*，we get

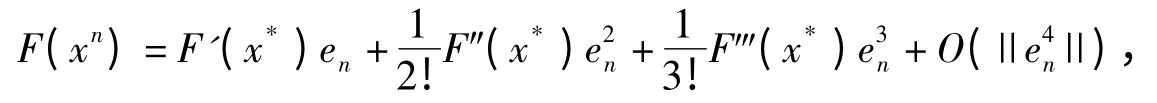
then，

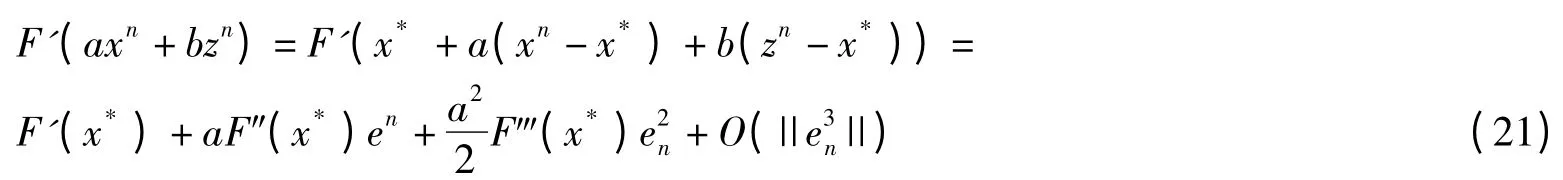
and

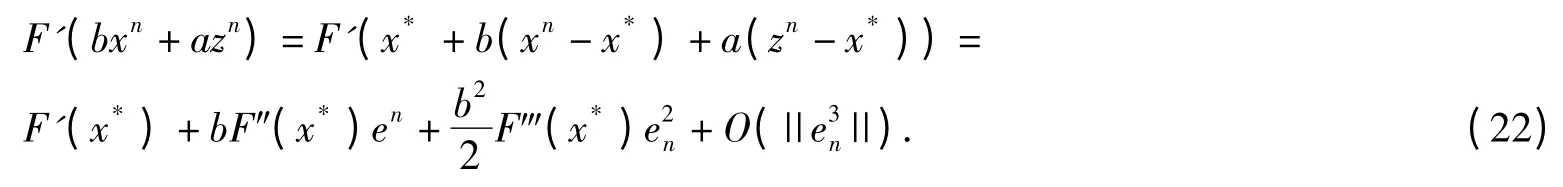
Combining (19)，(21)and (22)，we have

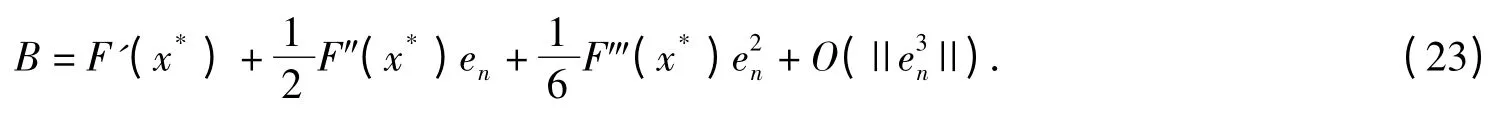
Combining (20)and (23)，we have

which means(12)has fourth-order convergence. □

Proof of Theorem2Since M.T.Danvishi and A.Barati had proven that (6)has third-order convergence，i.e.

Using the method in proof of Theorem1，we obtain (13)has fourth-order convergence. □

4 Numerical experiments

To check the effectiveness of two kinds of improved iterative formulas in this paper，we compare the error of different iterative schemes ((4)，(5)，(6)，(7)，(8)，(9)，(10)，(11)，(12)，(13))in each iteration the approximate solution and exact solution of the equation.All results are achieved at Matlab R2011b environment.When the error is less than the minimum positive 2.225 ×10-308in the Matlab，the result shows 0.

Example 1To solve the nonlinear equations:

The equations have an exact solution (1，1)T，we choose (1.5，1.5)Tas the initial value here.If the error is less than 0.00001，the program terminates.We solve the nonlinear equations by employing the above-mentioned iterative schemes，after each iteration，we get the error of the approximate solution and exact solution，see Tab. 1.

Tab. 1 The comparison between (4)to (11)and (12)，(13)

From the results in Tab.1，we know that the convergence speed of (4)to (11)is good. However，the two kinds of improved iterative formulas in our paper are better.

［1］Dai L，L，Tan J Q. The two kinds of iterative methods to solve systems of nonlinear equations with forth-order convergence［J］. Numerical Methods and Computer Applications，2012，33(2):121-128.

［2］KantorovicˇL V. The principle of the majorant and Newton′s method［J］. Doklady Akad Nauk SSSR (N.S.)，1951，76:17-20.

［3］Fang L，He G P. Some modifications of Newton′s method with higher-order convergence for solving nonlinear equations［J］. J Comput Appl Math，2009，228(1):296-303.

［4］Sˇamanskiǐ V E. On a modification of the Newton method［J］. Ukrain Mat Zˇ，1967，19(1):133-138.

［5］Wang X F. A variant newton′s iteration method［J］. Journal of Changchun University of Science and Technology:Natural Science Edition，2010(1):178-179.

［6］Darvishi M T，Barati A. A third-order newton-type method to solve systems of nonlinear equations［J］. Applied Mathematics and Computation，2007，187(2):630-635.

［7］Darvishi M T，Barati A. Super cubic iterative methods to solve systems of nonlinear equations［J］. Applied Mathematics and Computation，2007，188(2):1678-1685.

［8］Noor M A，Waseem M. Some iterative methods for solving a system of nonlinear equations［J］. Computers and Mathematics with Applications，2009，57(1):101-106.

［9］Gao R D. The newton′s method based on the gauss quadrature formula［J］. Value engineering，2010(10):118-119.

［10］Adomian G. Comments on a“counterexample”to decomposition［J］. Journal of Computational and Applied Mathematics，1989，26(3):375-376.

［11］Adomian G. Stochastic systems［M］.New Yourk:Academic Press，1983.