Weakly Almost Clean Rings

MENG Wenjing，CHEN Huanyin

（School of Science，Hangzhou Normal University，Hangzhou 310036，China）

1 Introduction

Through this paper，all rings are commutative with identity unless otherwise stated.In what follows，Z denotes the ring of integers and for a positive integern，Znis the ring of integers modulon.We writeId（R），reg（R）andZ（R）for the set of idempotents ofR，the set of regular elements ofRand the set of zero divisors ofR，respectively.

A ringRis clean if for eachx∈Rcan be written in the formx＝u＋ewhereu∈U（R）ande∈Id（R）.Such type of rings were extensively studied by many authors（see［1-5］）.In［1］，the author called a ringRis a weakly clean ring if every element is a sum or a difference of a unit and an idempotent.We know that a nonzero elementrin a ringRis said to be regular ifris not a zero divisor.A ringRis an almost clean ring if every elementx∈Rcan be written in the formx＝r＋ewherer∈reg（R）ande∈Id（R）.

Combining weak cleanness and almost cleanness，we introduce a new type ringRcalled weakly almost clean ring for which every elementx∈Ris of the formx＝r＋eorx＝r-ewherer∈reg（R）ande∈Id（R）.Various properties of weakly almost clean rings are investigated.LetRbe an indecomposable ring.We prove thatRis a weakly almost clean ring if and only if forx∈R＼reg（R），x＋1 orx-1 is regular.Contract to weakly clean rings（see［1］），we prove thatRis a weakly almost clean ring if and only ifR［X］is weakly almost clean.In addition，we show that for a nonempty collection｛Ri｝of ringsRi，the productR＝∏i∈IRiis weakly almost clean if and only if there existsm∈Isuch thatRmis weakly almost clean andRnis almost clean for alln≠m.LetRbe a ring andMbe anR-module.We finally prove that the trivial extensionR（M）ofRandMis weakly almost clean if and only if eachx∈Rcan be written in the formx＝r＋eorx＝r-ewherer∈R-（Z（R）∪Z（M））ande∈Id（R）.These extend the corresponding results on almost clean rings.

2 The Main Results

Definition 1A ring R is a weakly almost clean ring if every elementx∈Rcan be written asx＝r＋eorx＝r-ewherer∈reg（R）ande∈Id（R）.

Clearly，every weakly clean ring is weakly almost clean.But a weakly almost clean ring may be not a weakly clean.For example，integral domain Z.As any integral domain is weakly almost clean while an integral domain being indecomposable is weakly clean if and only if eitherRis local orRhas two maximal ideals and 1∈U（R）（see［1，Theorem 2.16］）.

Likewise，we could define anS-weakly almost clean ring.

Definition 2LetRbe a ring and letS⊆Id（R）.A ringRisS-weakly almost clean if eachx∈Rcan be written asx＝r＋eorx＝r-ewherer∈reg（R）ande∈S.

Note that every local ring is｛0，1｝-weakly almost clean.IfRisS-clean ring，by［2，Lemma 7］，thenS＝Id（R）.But theS-weakly almost clean rings behave different as the following example shows.

Example 1LetR＝Z3×Z3.Now Z3has characteristic not equal to 2 since 2（1，1）≠0，so by［1，Lemma 2.12（3）］，Ris a｛0，1｝-weakly clean ring，and then｛0，1｝-weakly almost clean ring.ButS＝｛（0，0），（1，1）｝⊂Id（R）＝｛（0，0），（0，1），（1，0），（1，1）｝.

A ringRis indecomposable providedId（R）＝｛0，1｝，we have the following result.

Theorem 1LetRbe an indecomposable ring.Then the following conditions are equivalent.

（1）Ris a weakly almost clean ring.

（2）Forx∈R＼reg（R），x＋1 orx-1 is regular.

Proof（1）⇒（2）Letx∈R＼reg（R）.SinceRis an indecomposable ring，sox＝r＋1 orx＝r-1 wherer∈reg（R），thusx＋1 orx-1 is regular.

（2）⇒（1）Letx∈R.Ifxis not regular then there existsx＋1 orx-1 is regular.Thereforex＝r＋1 orx＝r-1 wherer∈reg（R）.Ifxis regular，thenx＝x＋0.ThusRis a weakly almost clean ring. □

Corollary 1LetRbe an indecomposable weakly almost clean ring.Then for any idealIconsisting of zero divisors and for any zero divisorb，there existsa＝1 ora＝-1 such thata∉b＋I.

ProofSuppose that there exists an idealI⊆Z（R）andb∈Z（R）such thata∈b＋I.Then for eachathere existsi∈Isuch thata＝b＋i.Thus，bis not regular norb-afor eacha，by Theorem 1，which is a contradiction. □

Lemma1LetRbe a ring.ThenId（R）＝Id（R［X］）.

ProofIt is obvious by［1，Lemma 3.17］. □

Theorem 2LetRbe a ringR.Then

（1）R［X］is a weakly almost clean ring if and only ifRis weakly almost clean.

（2）R［［X］］is a weakly almost clean ring if and only ifRis weakly almost clean.

Proof（1）⇒Suppose thatR［X］is a weakly almost clean ring.Leta∈R⊆R［X］and writea＝r＋eora＝r-ewherer∈reg（R［X］）ande∈Id R［X］.Then by Lemma 1，Id（R）＝Id（R［X］）anda∈R，r＝a-eorr＝a＋emust be inR.Sor∈R∩reg（R［X］）＝reg（R）.ThenRis weakly almost clean.

⇐Letf（X）＝r0＋r1X＋…＋rn X n∈R［X］.Suppose thatRis a weakly almost clean ring，thenr0＝r＋eorr0＝r-ewherer∈reg（R）ande∈Id（R）.Sof（X）＝e＋r＋r1X＋…＋rn X norf（X）＝-e＋r＋r1X＋…＋rn X nsetg（X）＝r＋r1X＋…＋rn X n.Then we should prove thatg（X）∈reg（R［X］）.Letg（X）h（X）＝0 whereh（X）＝s＋s1X＋…＋sm X m，thenrs＋（r1s＋rs1）X＋（rs2＋r1s1＋r2s）X2＋…＝0.Thusrs＝0，r1s＋rs1＝0，rs2＋r1s1＋r2s＝0，….Sincer∈reg（R），sos＝0，ands1＝s2＝…＝sm＝0，thenh（X）＝0，Thusg（X）∈reg（R［X］）ande∈Id（R）＝Id（R［X］）.

（2）⇒Suppose thatR［［X］］is a weakly almost clean ring.Leta∈R⊆R［［X］］and writea＝r＋eora＝r-ewherer∈reg（R［［X］］）ande∈Id R（［［X］］）.Then by［1，Lemma 3.17］，Id（R）＝Id（R［［X］］）anda∈R，r＝a-eorr＝a＋emust be inR.Sor∈R∩reg（R［［X］］）＝reg（R）.ThenRis weakly almost clean.

⇐Letf（X）＝thenf（X）＝r0＋r1X＋….Suppose thatRis a weakly almost clean ring，thenr0＝r＋eorr0＝r-ewherer∈reg（R）ande∈Id（R）.So

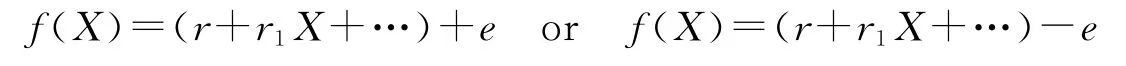
whereg（X）＝r＋r1X＋….Ifg（X）∉reg（R［［X］］），then there existsh（x）≠0 satisfyingg（x）h（x）＝0，thusrh（x）＝0，which is contradiction.Sog（X）∈reg（R［［X］］）ande∈Id（R）＝Id（R［［X］］）. □

By induction，we easily obtain the following result.

Corollary 2LetRbe a ring.Then

（1）R［X1，X2，…，Xn］is a weakly almost clean ring if and only ifRis weakly almost clean.

（2）R［［X1，X2，…，Xn］］is a weakly almost clean ring if and only ifRis weakly almost clean.

Theorem 3Let｛Ri｝be a nonempty collection of ringRi.Then the productR＝∏i∈IRiis weakly almost clean if and only if there existsm∈Isuch thatRmis weakly almost clean andRnis almost clean for alln≠m.

Proof⇐SupposeRmis weakly almost clean andRnis almost clean for alln≠m.Letx＝（xi）∈Rwe can writexm＝rm＋emorxm＝rm-emwhererm∈reg（Rm）andem∈Id（Rm）.

CaseⅠ.xm＝rm＋em.Forn≠m，letxn＝rn＋en，wherern∈reg（Rn）anden∈Id（Rn）.

CaseⅡ.xm＝rm-em.Forn≠m，let-xn＝-rn＋enwherern∈reg（Rn）anden∈Id（Rn），soxn＝rn-en.

Thenr＝（ri）∈reg（Ri），e＝（ei）∈Id（Ri），andx＝r＋eorx＝r-e.

⇒Suppose thatRis weakly almost clean.Then for each（x，0，…）∈R，

（x，0，…）＝（r，r1，r2，…）＋（e，e1，e2，…） or （x，0，…）＝（r，r1，r2，…）-（e，e1，e2，…）

where（r，r1，r2，…）∈reg（R）and（e，e1，e2，…）∈Id（R），sor∈reg（R1）ande∈Id（R1）.SoR1is weakly almost clean.Similarly，Riis weakly almost clean.Assume that there exists two indicesmandnsuch that neitherRmnorRnare almost clean.Then there existsxm∈Rmandxn∈Rnsuch thatxmis not a sum of a regular and an idempotent andxnis not a difference of a regular and an idempotent.Thus（xm，xn）is not weakly almost clean inRm×Rn，which is a contradiction. □

As is well known，every homomorphic image of weakly clean rings is weakly clean as well.We next show that this not the case for weakly almost clean rings.

Example 2LetR＝K［X，Y，Z］whereKis a field.SoRbeing an integral domain is weakly almost clean.Let＝K［X，Y，Z］／（X（X-1）（X＋1）Y）.Note thatis indecomposable.Hereandare zero divisors，sois not weakly almost clean，in terms of Theorem 1.

LetRbe a ring andMbe anR-module.The set of pairs（r，m）withr∈Randm∈M，under coordinatewise addition and the multiplication defined by（r，m）（r′，m′）＝（rr′，rm′＋r′m），for allr，r′∈R，m，m′∈M.ThenR（M）is called the trivial extension ofRbyM.

Lemma 2LetRbe a ring and letMbe anR-module.Then（r，m）∈Z（R（M））if and only ifr∈Z（R）∪Z（M）.

ProofSee［1，Theorem 3.21］. □

Theorem 4LetRbe a ring andMbe anR-module.Then the trivial extensionR（M）ofRandMis weakly almost clean if and only if eachx∈Rcan be written in the formx＝r＋eorx＝r-ewherer∈R-（Z（R）∪Z（M））ande∈Id（R）.

ProofWe first observe thatId（R（M））＝｛（e，0）∈R（M）｜e∈Id（R）｝.Suppose（e，m）∈Id（R（M）），so（e，m）＝（e，m）2＝（e2，2em）.Hencee＝e2andm＝2em.Soem＝2e2m＝2emgivesem＝0 and hencem＝2em＝0.So we easily prove the equality.Also，（r，m）∈Z（R（M））if and only ifr∈Z（R）∪Z（M）by Lemma 2.

⇒Suppose thatR（M）is weakly almost clean.Letx∈R，sinceId（R（M））＝｛（e，0）∈R（M）｜e∈Id（R）｝，（x，0）＝（r，0）＋（e，0）or（x，0）＝（r，0）-（e，0）where（r，0）∈reg（R（M））and（e，0）∈Id（R（M））.Since（r，0）∈reg（R（M）），r∈R-（Z（R）∪Z（M）），and sox＝r＋eorx＝r-ewherer∈R-（Z（R）∪Z（M））ande∈Id（R）.

⇐Letx∈Randm∈M.Writex＝r＋eorx＝r-ewherer∈R-（Z（R）∪Z（M））ande∈Id（R）.Then（x，m）＝（r，m）＋（e，0）or（x，m）＝（r，m）-（e，0）where（r，m）∈reg（R（M））and（e，0）∈Id（R（M））. □

Corollary 3LetRbe a ring.Thenis weakly almost clean if and only ifRis weakly almost clean.

ProofIt is obvious by Theorem 4. □

Corollary 4LetRbe a ring，Mbe anR-module andZ（M）＝｛0｝.Then the trivial extensionR（M）ofRandMis weakly almost clean if and only ifRis weakly almost clean.

ProofIt is obvious by Theorem 4. □

Example 3The trivial extension Z（Z6）of Z and Z6is not weakly almost clean.Clearly，Z（Z）＝｛0｝as Z is an integer domain.Further，Z（Z6）＝2 Z∪3 Z，and so Z-Z（Z6）＝｛m∈Z｜2，3｝.We easily check that 3，3-1，3＋1Z-Z（Z6）.Therefore Z（Z6）of Z and Z6is not weakly almost clean，in terms of Theorem 4.

Example 4The trivial extension Z（Z15）of Z and Z15is weakly almost clean.Clearly，Z（Z）＝｛0｝as Z is an integral domain.Further，Z（Z15）＝3 Z∪5 Z，and so Z-Z（Z15）＝｛m∈Z｜3，5｝.Letx∈Z.

CaseⅠ.3，5.Thenx＝0＋xwithx∈Z-Z（Z15）.

CaseⅡ.3｜x.Thenx＝3mfor somem≥0.Then 3 3m-1，3m＋1.If 5｜3m-1，3m＋1，then 5｜2，an absurd.Hence，5 3m-1 or 3m＋1.This implies thatx-1，orx＋1 in Z-Z（Z15）.

CaseⅢ.5｜x.Thenx＝5mfor somem≥0.Then 5 5m-1，5m＋1.If 3｜5m-1，5m＋1，then 3｜2，an absurd.Thus，35m＋1 or 5m-1.This implies thatx＋1 orx-1 is in Z-Z（Z15）.

Therefore we conclude that Z（Z15）of Z and Z15is weakly almost clean，in terms of Theorem 4.

［1］Ahn Myung-Sook.Weakly clean rings and almost clean rings［D］.Iowa City：The University of Iowa，2003.

［2］Anderson D D，Camillo V P.Commutative rings whose elements are a sum of a unit and idempotent［J］.Comm Algebra，2002，30（7）：3327-3336.

［3］Tamekkante M，Chhiti M，Louartiti K.Generalization of almost clean rings［J］.International J Algebra，2011，25：1213-1218.

［4］Han J，Nicholson W K.Extension of clean rings［J］.Comm Algebra，2001，29：2589-2595.

［5］Chen H.Rings related to stable range conditions［M］.Hackensack：World Scientific Publishing Co pte ltd，2011.