集装箱堆场出口箱箱位分配多目标优化模型

刘婵娟，胡志华

（上海海事大学 物流研究中心，上海 201306）

0 引 言

集装箱运输在全球经济和贸易发展中发挥着重要作用.近年来随着集装箱港口数量的激增，港口之间的竞争日趋激烈.而堆场出口箱的堆存方式直接影响码头取箱装船作业的效率和码头运营成本，是提升港口竞争力的关键.对于出口箱堆场，各集装箱到场顺序无法预知、堆场密度过高时集装箱箱位优化空间有限、箱重信息不准、船舶配载计划临时改变等一些不可控随机因素，使得堆场出口箱堆存具有一定的复杂性.

针对堆场出口箱具体箱位分配问题，各国物流方面专家学者们提出了不同的方法和策略.很多学者将堆场箱位分配问题分解为几个阶段，将其变成一个多阶段决策问题.文献［1－4］均采用两阶段法进行堆场出口箱箱位分配.其中Chen等［1］和Hu等［2］，都是在第一阶段进行贝位选择，第二阶段解决具体箱位分配问题.Kim 等［3］运用两阶段法以最小化场内集卡运输距离和最小化翻箱率为目标进行堆场出口箱箱位分配.Zhang等［4］主要以最小化翻箱率为目标，运用两阶段法进行箱位分配.Kim 等［5］以装船前预翻箱数最少为目标，建立动态规划模型解决堆场出口箱箱位分配问题.靳志宏等［6］以降低集装箱堆场翻箱率为研究课题，并将此问题转化为求解动态规划最短路径问题，结合启发式算法选择具体箱位.Kang等［7］在出口集装箱箱重未知的情况下，利用基于模拟退火的搜索算法来获得出口箱在堆场的堆存策略，最小化堆场作业时翻箱量.Preston等［8］和Bazzazi等［9］运用遗传算法求解堆场出口箱箱位分配问题.Lim 等［10］以计划期内各个箱区之间的作业量不均衡最小化为目标函数，建立整数规划模型，对进入堆场的集装箱进行箱位分配.郝聚民等［11］提出了混合顺序堆场作业的概念，并且基于图搜索技术及模式识别理论提出了混合顺序作业贝位优化模型.文献运用启发式算法求解这一问题.李建忠等［12］从平衡箱区贝位箱量和最小化集卡行驶距离入手，在滚动计划的基础上，建立了集装箱堆场空间动态配置模型.该模型的主要目的是提高集卡作业效率，降低装船作业过程中堆场机械耗费成本.文献［13－15］均运用数学规划的方法解决堆场箱位分配问题.文献［16］利用搜索技术理论提出了出口箱箱位合理分配及减少倒箱率的措施，其与前述文献最大的不同之处是认为贝位中缓冲箱位的位置是固定的，这与现实操作过程不完全相符.本文中假定缓冲箱位的位置并不固定.

以上文献多是只考虑使装船操作过程中翻箱数最少或是只考虑在装船操作中场内集卡行驶距离最小为目标，本文以最小化堆栈中不满足重量约束的箱子数，最小化不满足时间先后顺序的箱子数，最小化Bay内堆存成本以及均衡各堆栈内集装箱数量为目标，提出基于堆场出口箱堆存原则的多目标混合整数规划模型对出口集装箱进行具体箱位分配.

1 问题描述与假设

集装箱堆场划分为不同的区（Block），每个区由多个贝位（Bay）、每个贝位由若干列（Row）和层（Tier）组成.所以堆场箱位由箱区、贝位、列和层来表示.如A10112表示该箱在A1区01贝位第1列第2层；A10213表示该箱在A1区02 贝位第1列第3层.而贝位内在竖直方向堆放的一个或多个集装箱称为栈（Stack）.在我国，大多数集装箱码头中使用轮胎龙门吊，一般情况下最常见的每个贝位由6列4层组成，即一个贝位中能堆装24个集装箱，见图1.为了减少取箱装船过程中翻箱次数，堆场在进行箱位分配时首先将出口箱按船名和重量级进行分组，本研究将出口箱按重量分为3个等级.此外，为了减少集卡及场桥移动距离，通常将要装载到同一艘船的集装箱尽可能同贝堆放或放在同一箱区.

图1 集装箱堆场贝位示意图Fig.1 Illustration of container yard bays

出口箱堆存涉及集港计划、堆场分类堆存计划与安排、具体箱位优化分配、取箱顺序优化等过程.本文中假定到场出口箱已按船名、目的港分类，主要研究具体箱位分配优化问题.为了便于集装箱装卸，通常情况下，出口箱在堆场的堆存必须遵 循 一 定 的 规 则：（1）LBH（light below the heavy）即“轻 箱 在 下，重 箱 在 上”原 则；（2）EAES（early arrive early store）即“先到场，先堆存”原则；（3）取箱装船就近原则；（4）各堆栈内集装箱数均衡原则.

本文按照出口箱堆场堆存原则，将堆场出口箱箱位选择优化问题转化为：（1）使贝位内不满足LBH 原则的箱子数最少；（2）使贝位内不满足EAES原则的箱子数最少；（3）使取箱装船作业过程场内集卡运输成本最小；（4）使每一贝位中各个堆栈箱子数尽量均衡分布.研究考虑以下假设条件：（1）不考虑集装箱大小差异，假定所有箱子全为标准6.096m 集装箱；（2）不考虑冷藏箱、危险品箱等特殊箱的堆存，只针对普通重箱；（3）集装箱组别已按船名和目的港确定；（4）每组集装箱对应的船舶配载方案已知；（5）场内集卡运输每个集装箱的成本只与集卡移动距离有关；（6）不同重量级集装箱混合堆存.

2 模型建立

2.1 符号说明

（1）集合：I＝｛1，2，3，…，Ni｝，所有出口集装箱的集合，Ni为到场集装箱总数，通过i，j∈I索引；B＝｛1，2，3，…，Nb｝，箱区内贝位集合，Nb为箱区内贝位总数，通过b∈B索引；R＝｛1，2，3，…，Nr｝，贝位内列数的集合，Nr为贝位内总列数，通过r∈R索引；T＝｛1，2，3，…，Nt｝，贝位内层数的集合，Nt为贝位内总层数，通过t∈T索引.

（2）参数：Ei，j表示贝位内满足EAES原则的箱子，当集装箱i和j的放置满足时间先后顺序时Ei，j取1，否则取0；Wi，j表示贝位内满足LBH原则的箱子，当集装箱i和j的放置满足重量约束时Wi，j取1，否则取0；Ob，r，t表示贝位内已被占用的箱位.

（3）决策变量：xi，b，r，t∈｛0，1｝，如果集装箱i被放 置 在b贝r列t层 时xi，b，r，t为1，否 则 为0；yi，j，b，r，t1，t2∈｛0，1｝，如 果 集 装 箱i和j被 分 配 到（b，r，t1）和（b，r，t2）两个箱位时yi，j，b，r，t1，t2为1，否则为0；zwi，j，b，r，t1，t2∈｛0，1｝，如果i和j两个集装箱的堆存满足LBH原则zwi，j，b，r，t1，t2为1，否 则 为0；zei，j，b，r，t1，t2∈｛0，1｝，如果i和j两 个集装箱的堆 存满足EAES原则zei，j，b，r，t1，t2为1，否则为0.

2.2 模 型

2.2.1 基本模型 不满足LBH 原则和不满足EAES原则的箱子都会导致翻箱操作.所以，在基本模型［M1］中，目标函数表示使取箱装船过程中翻箱次数最少，其由两部分组成，其中fw表示贝位内不满足LBH 原则的集装箱数量；fe表示贝位内不满足EAES原则的集装箱数量.

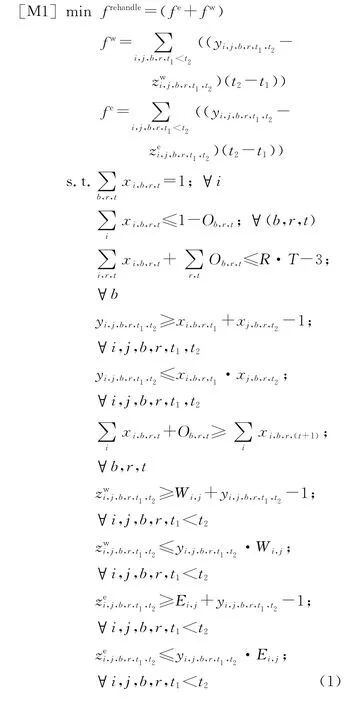
约束条件（1）表示一个集装箱只能占用一个箱位；（2）表示一个箱位只能放一个箱子；（3）表示某一贝位内堆存集装箱总数不能超过贝内箱位数，文中假定每贝由6列4层构成，且有3个缓冲箱位，则贝内可堆存集装箱数最多为21个；（4）和（5）表示决策变量yi，j，b，r，t1，t2和xi，b，r，t之间的关系，只有当集装箱i和j分别分配给箱位（b，r，t1）和（b，r，t2）时，决策变量yi，j，b，r，t1，t2的值取1，否则为0；（6）表示箱子不能悬空放置；（7）和（8）表示决策变量zwi，j，b，r，t1，t2与yi，j，b，r，t1，t2和Wi，j之间的关系，当i放在j下面，且i比j轻 时，zwi，j，b，r，t1，t2取1，否则为0；（9）和（10）表示决策变量zei，j，b，r，t1，t2与yi，j，b，r，t1，t2和Ei，j之间的关系，当i在j下面，且i比j早到堆场时，zei，j，b，r，t1，t2取1，否则为0.

2.2.2 堆场出口箱箱位分配多目标优化模型 考虑到堆场出口箱堆存成本和使各堆栈集装箱堆存高度均衡，在模型［M1］的基础上，提出两个新的目标：fb表示存储成本；fh表示各堆栈中箱子堆存高度.建立堆场出口箱箱位分配多目标优化模型［M2］.其中Cb表示b贝位内的集装箱在取箱装船过程中集卡运输成本，该成本与贝位距岸边的距离成正比，Cb∈｛1，2，3，…，B｝，通过b∈B索引.

模型［M2］所示的多目标规划模型无法利用已有的混合整数规划求解器进行直接求解.因此，在模型［M2］的基础上，提出了模型［M3］和［M4］对此问题进行优化.其中［M3］是对目标函数fh的最小值进行求解，即使贝位内各堆栈箱子数尽量均衡，避免堆存过高.［M4］是将目标函数fh和fb作为一个整体进行优化，此过程分为两个阶段.第一阶段是根据［M3］求出目标函数fh的最小值，令其等于fh＊；第二阶段是对目标函数fb的优化，其中α是目标函数fh的松弛系数.

3 算例证明

为验证模型的有效性，本文应用MATLAB软件编程，在Intel（R）－32Core（TM）i5－4300U＠1.90GHz计算机上，利用CPLEX 求解器进行求解.以实际最常见的每贝6列4层堆场为例，假定每个贝位中有3个箱位为缓冲箱位.本文所研究的堆场箱位分配范围涉及1、2、3个贝位.

算例1 当堆场某个箱区有1个贝位时，16个集装箱到场时间顺序和重量等级分布见表1.已知所有进场集装箱已按船名、目的港分组，这16个集装箱需要被装载到同一艘船上.这一贝位内集装箱在取箱装船作业中集卡运输成本为1，已经被占用的箱位数Ob，r，t为0.利用MATLAB软件编程求解上述算例，得到这16个集装箱具体箱位分配见图2.

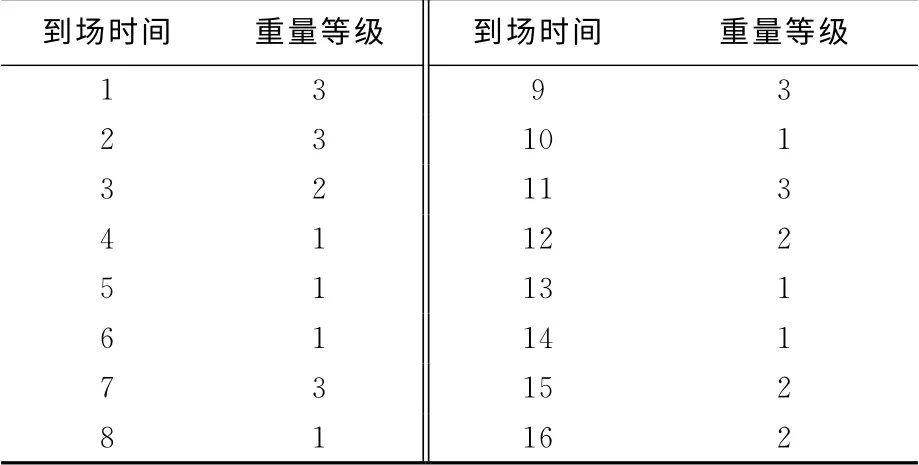
表1 16个随机到港集装箱的时间顺序和重量分布Tab.1 The time sequence and weight distribution of 16containers arriving to yard stochastically

图2 16个集装箱具体箱位分配Fig.2 Specific space allocation of 16containers

算例2 当堆场某个箱区有2个贝位时，18个集装箱到场时间顺序和重量分布见表2.已知这18个集装箱同样已按船名、目的港分组.Bay 1中集装箱在取箱装船作业中集卡运输成本为1，Bay 2中集装箱在取箱装船作业中集卡运输成本为2.Bay 1中第一列和Bay 2中第一列的共计8个箱位已被占用，如图3中阴影部分所示.求解得到这18个集装箱具体箱位分配如图3中（a）和（b）所示.

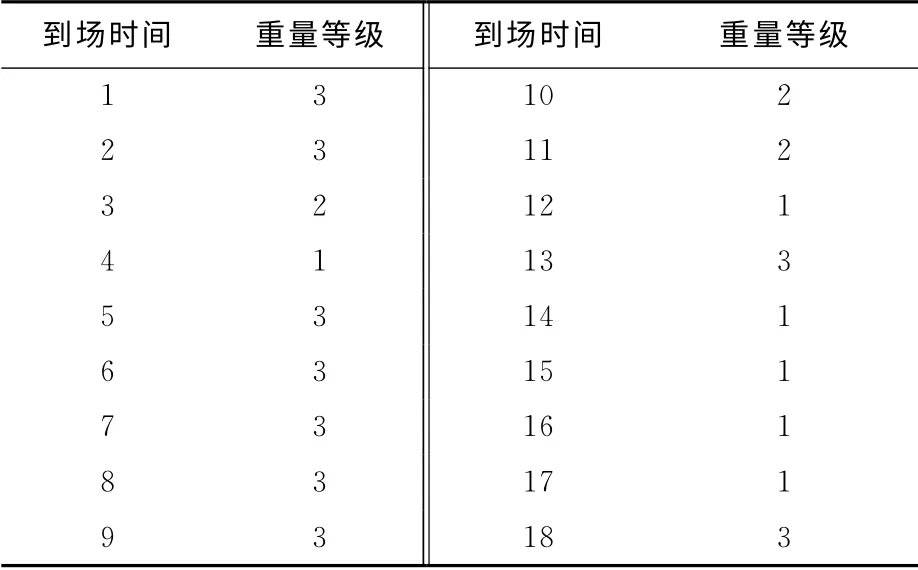
表2 18个随机到港集装箱的时间顺序和重量分布Tab.2 The time sequence and weight distribution of 18containers arriving to yard stochastically

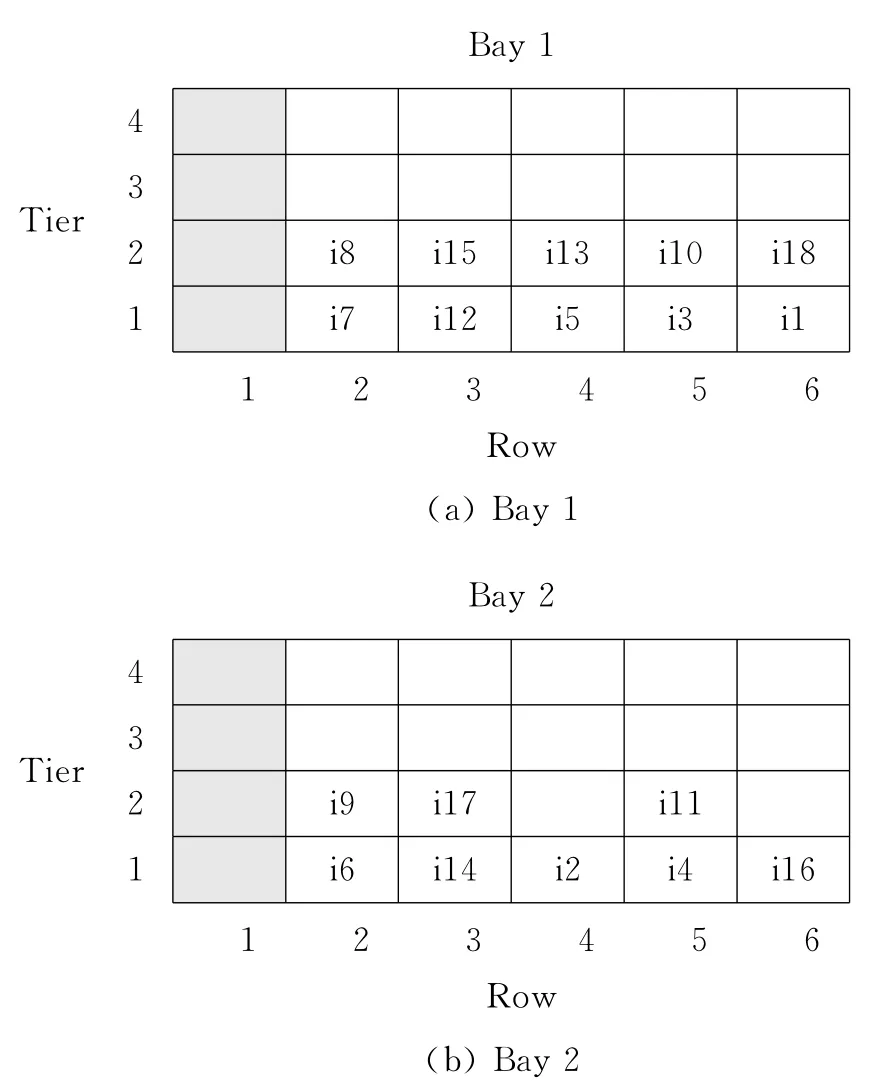
图3 18个集装箱具体箱位分配Fig.3 Specific space allocation of 18containers

由图3所得结果可知，当Bay 1、Bay 2 中各有4个箱位已被占用，则每个贝位内最多只能堆存17个集装箱.Bay 1内集装箱存储成本为1，低于Bay 2内存储成本，为了满足取箱操作过程中场内集卡运输距离最小，节约堆场作业成本，在满足LBH 原则和EAES原则的前提下，集装箱被优先分配在Bay 1内，存储这18个出口箱的最低成本为26.

算例3 当堆场某个箱区有3个贝位时，20个集装箱到场时间顺序和重量分布见表3.已知这20个集装箱同样是已按船名、目的港分组的.Bay 1、Bay 2、Bay 3中集装箱在取箱装船作业中集卡运输成本分别为1、2、3.已知Bay 1中1～3列，Bay 2中1～3列，共计24个箱位已被占用，如图4中阴影部分所示.利用MATLAB 软件编程求解上述算例，得到这20个集装箱具体箱位分配如图4（a）～（c）所示.

根据图4结果可知，当Bay 1 和Bay 2 中 各有12个箱位已被占用，则Bay 1和Bay 2内最多只能各堆存9个集装箱.3个贝位中Bay 1的存储成本最小为1，其次是Bay 2为2，Bay 3中存储成本最高，所以为了满足取箱操作过程中场内集卡运输距离最小，节约堆场作业成本，在满足LBH原则和EAES原则的前提下，集装箱被优先分配在Bay 1和Bay 2内.

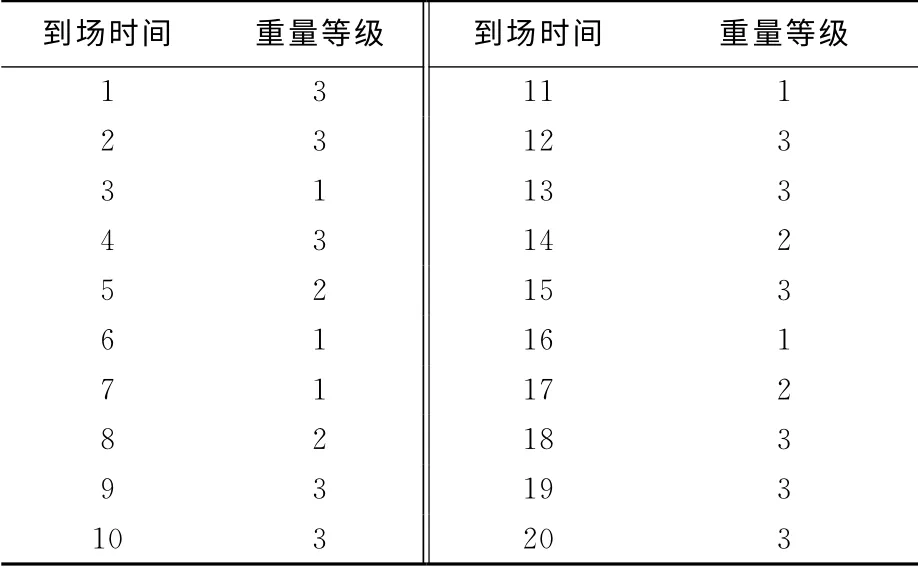
表3 20个随机到港集装箱的时间顺序和重量分布Tab.3 The time sequence and weight distribution of 20containers arriving to yard stochastically

图4 20个集装箱具体箱位分配Fig.4 Specific space allocation of 20containers

4 结果分析

基于以上3 组算例，本文使用MATLAB（R2013a）软件编程对模型进行求解，得出最优解.并得到fw、fe、fh、fb，见表4.其中fw和fe均为0.这表明应用此模型对堆场出口箱进行箱位分配能够尽可能避免取箱装船作业过程中出现翻箱操作.

为了探究模型中的参数对实验结果的影响，以及权衡堆场出口箱堆存的4个原则对具体箱位分配的影响，本文设计了如表5所示的3个实验，分别对这些因素造成的影响进行研究.

基于以上3个实验，对所得结果结合图5～8进行分析得出以下结论：

表4 3组算例所得目标函数值Tab.4 Objective function value of three groups of examples

表5 实验目的及配置Tab.5 Experimental purpose and settings

（1）由实验1的结果可知，如图5所示，参数Ob，r，t的变化对目标函数fw、fe并无影响.算 例1中，当只有1个贝位时，参数Ob，r，t的改变也不会影响目标函数fb的值.算例2中，当有2个贝位时，目标函数fb和fh的值会随着已被占用箱位数的变化而变化.总体上，已被占用的箱位数越多，目标函数fh的值越大，即堆栈越高.集装箱堆存太高可能发生倒塌，存在安全隐患.此外，贝内堆栈高度分布不均衡将会增加取箱装船过程中场桥移动距离，加大机械作业成本.

（2）由实验2的结果可知，假如不考虑各堆栈中箱子数均衡原则，即在模型［M2］中去掉fh，则箱位分配方案会发生改变，如图6所示.两种分配方式所得目标函数fb、fh见图7.由实验结果可知，在考虑各堆栈箱子数均衡原则的情况下，集装箱堆存成本较高，为26.而不考虑各堆栈箱子数均衡原则的情况下，堆存成本只有19.相反，在考虑各堆栈箱子数均衡原则的情况下，目标函数fh的值仅为42，不考虑各堆栈箱子数均衡原则的情况下，fh的值为110，即考虑各堆栈箱子数均衡原则的情况下，集装箱明显地堆存于较低层.这样不但提高了堆栈的安全性，而且有利于取箱装船过程中减少场桥上下移动距离，降低机械作业成本.

（3）以算例2中18个集装箱数据为例，对目标函数fh和fb进行均衡分析，结合图8可知：当目标函数fh在0.8～2.4时，存储成本fb几乎呈线性减少.而当fh大于2.4时，存储成本fb保持为19不再改变.当fb在20～26时，两个目标可以同时优化.

（4）综合以上分析，为减少堆场出口箱堆存的经济成本，集装箱进场后应该优先选择近泊位箱区和贝位存放；为了提高堆场作业效率，尽可能避免取箱装船过程出现翻箱并且使各堆栈中箱子数尽量均衡，集装箱进场时应优先选取空贝位或贝位中已被占用箱位较少的贝进行堆存.

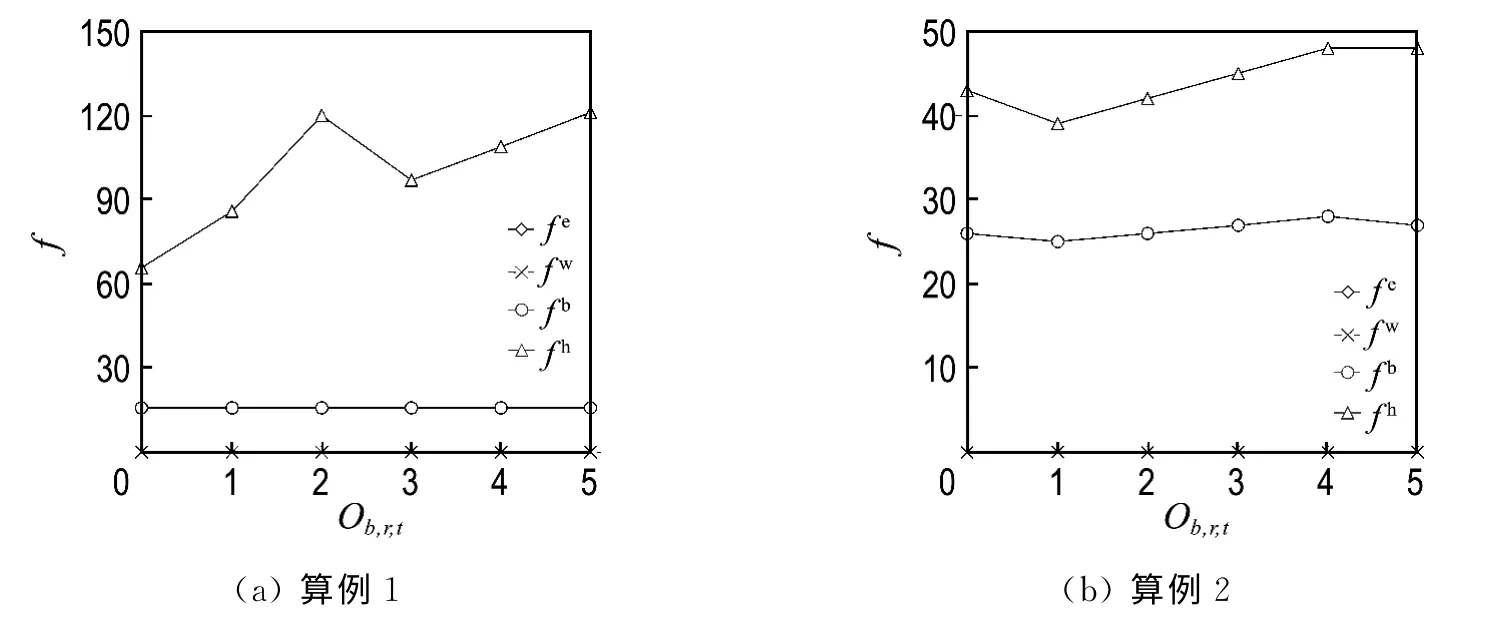
图5 参数Ob，r，t对目标函数值的影响Fig.5 The influence of parameter Ob，r，ton the objective function value

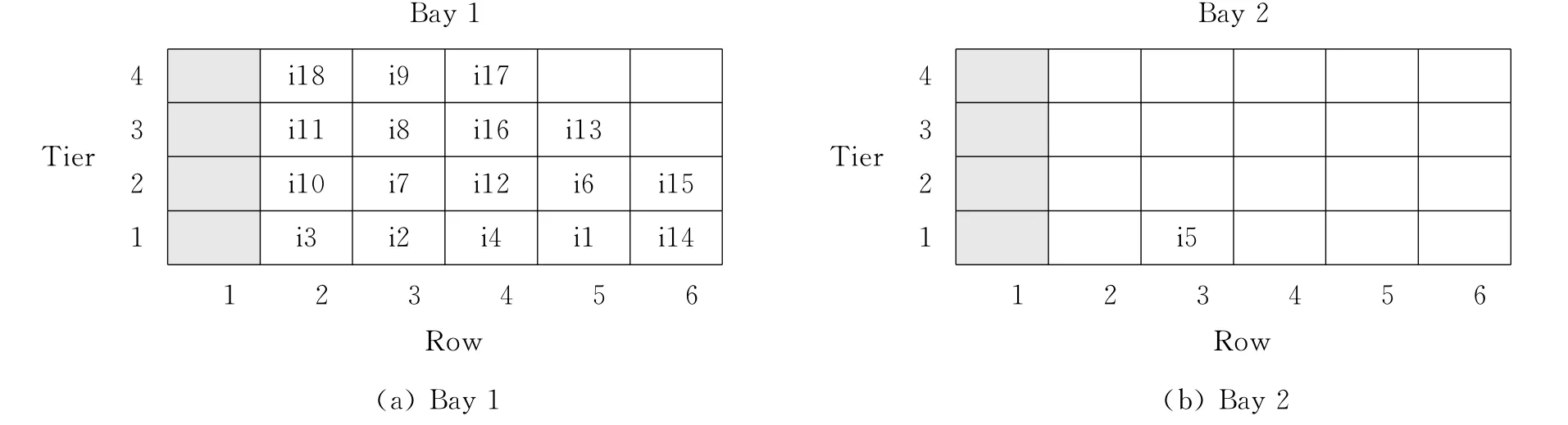
图6 不考虑堆栈中箱子数均衡原则下18个箱子箱位分配Fig.6 Specific space allocation of 18containers without considering the number equilibrium in each stack

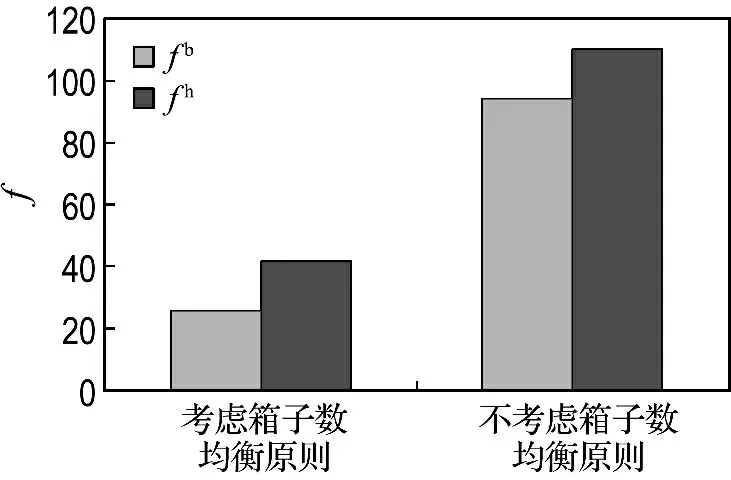
图7 两种不同分配方式所得fb 和fhFig.7 fb and fh in two different distribution ways

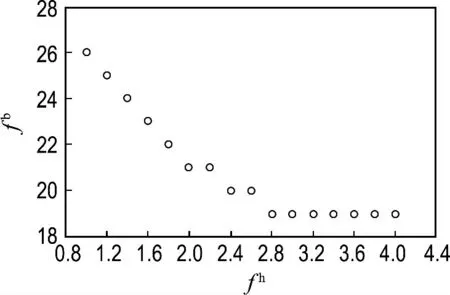
图8 fh 和fb 之间的均衡Fig.8 The tradeoff analysis between fb and fh

5 结 语

基于堆场出口箱堆存原则的多目标混合整数规划模型，在充分考虑出口箱到场时间的随机性和堆场贝位中不同重量级别集装箱混装的情况下，能够尽可能地降低或者消除取箱装船时翻箱操作的出现次数，且使取箱装船过程中场内集卡运输距离最小，从而达到提高装船时作业效率和节约堆场机械设备耗费成本的目的.同时还可以缩短出口箱装船时间和船舶在港停留时间，避免给船公司和港口造成较大时间损失.大量算例证明此模型能够从整体上对堆场出口箱箱位分配进行优化.与只考虑最小化翻箱率的研究相比，此分配方案更加合理.

［1］ CHEN Lu，LU Zhi－qiang.The storage location assignment problem for outbound containers in a maritime terminal ［J］.International Journal of Production Economics，2012，135（1）：73－80.

［2］ HU Wen－bin，WANG Huan，MIN Zhen－yu.A storage allocation algorithm for outbound containers based on the outer–inner cellular automation［J］.Information Sciences，2014，281：147－171.

［3］ Kim Kap－hwan，Park Kang－tae.A note on a dynamic space－allocation method for outbound containers ［J］.European Journal of Operational Research，2003，148（1）：92－101.

［4］ ZHANG Chu－qian，LIU Ji－yin，Wan Yat－wah，et al.Storage space allocation in container terminals［J ］.Transportation Research Part B：Methodological，2003，37（10）：883－903.

［5］ Kim Kap－hwan，Park Young－man，Ryu Kwangryul.Deriving decision rules to locate export containers in container yards［J］.European Journal of Operational Research，2000，124（1）：89－101.

［6］ 靳志宏，毛 钧，李 娜.基于混合动态规划的集装箱堆场贝位内翻箱作业调度优化［J］.交通运输系统工程与信息，2011，11（6）：131－136.JIN Zhi－hong，MAO Jun，LI Na.Scheduling of relocating containers within a bay in container yard based on hybrid dynamic programming［J］.Journal of Transportation Systems Engineering and Information Technology，2011，11（6）：131－136.（in Chinese）

［7］ Kang Jae－ho，Ryu Kwang－ryel，Kim Kap－hwan.Deriving stacking strategies for export containers with uncertain weight information［J］.Journal of Intelligent Manufacturing，2006，17（4）：399－410.

［8］ Preston P，Kozan E.An approach to determine storage locations of containers at seaport terminals［J］.Computers and Operations Research，2001，28（10）：983－995.

［9］ Bazzazi M，Safaei N，Javadian N.A genetic algorithm to solve the storage space allocation problem in a container terminal［J］.Computers and Industrial Engineering，2009，56（1）：44－52.

［10］ Lim A，Xu Z.A critical－shaking neighborhood search for the yard allocation problem ［J］.European Journal of Operational Research，2006，174（2）：1247－1259.

［11］ 郝聚民，纪卓尚，林 焰.混合顺序作业堆场BAY优化模型［J］.大连理工大学学报，2000，40（1）：102－105.HAO Ju－min，JI Zhuo－shang，LIN Yan.Study of optimization of a BAY of stacking［J］.Journal of Dalian University of Technology，2000，40（1）：102－105.（in Chinese）

［12］ 李建忠，丁以中，王 斌.集装箱堆场空间动态配置模型［J］.交通运输工程学报，2007，7（3）：50－55.LI Jian－zhong，DING Yi－zhong，WANG Bin.Dynamic space deployment model of container storage yard ［J］.Journal of Traffic and Transportation Engineering，2007，7（3）：50－55.（in Chinese）

［13］ Cordeau J F，Gaudioso M，Laporte G，etal.A memetic heuristic for the generalized quadratic assignment problem ［J］.INFORMS Journal on Computing，2006，19：433－443.

［14］ Malucelli F，Pallottino S，Pretolani D.The stack loading and unloading problem［J］.Discrete Applied Mathematics，2008，156（17）：3248－3266.

［15］ SauríS，Martín E.Space allocating strategies for improving import yard performance at marine terminals ［J］.Transportation Research Part E：Logistics and Transportation，2011，47（6）：1038－1057.

［16］ 计三有，高悦文.集装箱堆场减少倒箱率方法研究［J］.水运工程，2006（8）：53－56，61.JI San－you，GAO Yue－wen.Reduction of rate of container transportation in container yard［J］.Port＆ Waterway Engineering，2006（8）：53－56，61.（in Chinese）