基于混合人工鱼群优化SVR的交通流量预测
2015-03-20姚卫红方仁孝张旭东
姚卫红,方仁孝,张旭东
(大连理工大学 计算机科学与技术学院,辽宁 大连 116024)
0 引 言
准确、可靠的道路交通流量信息是智能交通系统中交通控制和信息管理的重要组成部分.在每天的车辆出行高峰时段,不准确的交通流量信息会增加出行者时间,造成道路拥堵、能源消耗和环境污染,所以高峰时段准确的交通流量预测就显得尤为重要[1-3].
传统的交通流量预测模型有基于数学测定方法的自回归移动平均方法(ARIMA)模型、卡尔曼滤波模型和非线性回归模型[4].这些模型有计算简单、速度快的优点,但是它们不能处理交通流量信息的不确定性和非线性的复杂特征.目前常用的交通流量预测模型有基于知识发现的智能模型,如模糊理论、小波理论和ANN 人工神经网络[5].ANN 模型由于其无先验性地解决高复杂度问题的良好性能在交通流量预测领域取得了一定的成果.但ANN 是基于经验风险最小化的,存在收敛速度慢和训练误差非凸的问题,难以求得最优解[3].
支持向量机(SVM)最早是为了解决模式识别和分类问题的,随着Vapnik的ε不敏感损失函数的引入,SVM 开始用于解决非线性回归估值问题,称之为支持向量回归(SVR).SVR 能很好地解决小样本、非线性和高维的问题,已经成功地用于交通系统领域的预测[2-3].然而,SVR 模型不能得到准确的预测结果是因为SVR 模型中参数组合C、ε和σ的值设置得不准确.传统的人工选择和网格遍历的方法存在主观经验判断和寻优时间长的缺点,并不能得到好的效果,但是运用智能的选择进化算法(如ACO、PSO 和AFS 等)优化SVR参数能选择到合适的回归参数[6-7].每 种 智能进化算法都有各自的优缺点.研究表明,采用混合优化算法比采用单一优化算法能取得更好的预测结果[8-9].
本文针对AFS算法的初始参数设置较多和步长因子的设置对寻优性能的影响的缺点,提出采用PSO 算法公式改进AFS算法,减小步长因子对AFS算法的影响,并且引入混沌机制初始化鱼群位置,来进行SVR 的参数选择,建立混沌粒子群人工鱼群混合优化SVR 的CPSOAFS-SVR交通流量预测模型.
1 SVR 模型
SVR 的核心思想是基于结构风险最小化原则,通过定义一个非线性映射将输入数据集映射到高维特征空间,在这个高维特征空间存在一个线性函数f能够明确地表示输入数据集和输出数据集之间的非线性关系.SVR 函数定义如下:
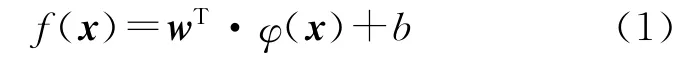
式中:f决定预测值,φ(·)为映射函数,x为输入数据向量,w和b分别为高维特征空间中的向量和常数,两者的值可以通过下式求得:
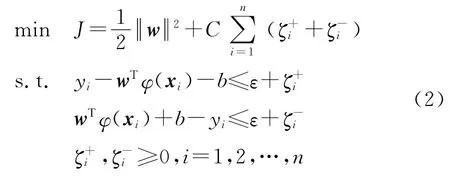
式中:C为惩罚系数,ε为不敏感损失函数的最大误差系数,ζ+i和ζ-i为松弛系数,n为输入数据的样本个数.SVR 致力于求解高维特征空间的最优超平面,使得输入输出数据集之间的整体误差最小.
通过求解上述带不等式约束的二次优化问题,可以得到式(1)中的参数向量w的值:

其中β*i和βi分别为运用拉格朗日乘子法求解二次优化问题的拉格朗日系数.最后SVR 问题就得到如下方程:

其中K(·)为计算高维特征空间中的两个输入向量内积的核函数.本文采用Gauss函数K(xi,xj)=exp(-xi-xj2/2σ2)作为模型的核函数.
SVR 模型中参数组合C、ε和σ的值的选择影响预测的精度,所以建立优化的交通流量预测模型就需要选取最优的参数组合来最小化实际值和预测值之间的误差[7].
2 CPSOAFS-SVR 预测模型
2.1 AFS算法
人工鱼群(AFS)算法是由李晓磊于2003年提出的通过模拟自然界中鱼群的行为得到的一种群智能优化算法[10].每条人工鱼代表D维空间中的一个点xi,人工鱼个体所在位置的适应度为Fi,本文的交通流量预测致力于Fi最小化.两条人工鱼之间的距离为xi-xj,其他的参数包含鱼群个数n、视野v、步长s和拥挤度δ.每条人工鱼通过模拟鱼的觅食、聚群、追尾和随机行为寻找最优适应度来进行搜索优化过程.
(1)觅食行为
觅食行为是人工鱼趋向较优适应度的基本行为.其计算公式为

式中:r1和r2分别代表随机变量区间[0,1]和[-1,1],xi代表第i条人工鱼位置信息,Fj为xi在视野范围内随机移动到另一位置xj的适应度.若反复尝试若干次后,仍不满足前进条件,则随机移动一步.
(2)聚群行为
聚群行为是人工鱼个体在游动过程中为了趋利避害,自然地聚集成群向邻居中心移动的行为.其计算公式为

其中ns为当前视野范围内的邻居数目,xc代表所有邻居的聚集群体的中心位置.当xc的适应度优于当前xi位置的适应度,并且鱼群不太拥挤时,xi就向中心位置移动.否则,执行觅食行为.
(3)追尾行为
追尾行为是一种向着附近的有更优适应度的人工鱼移动的行为.其计算公式为
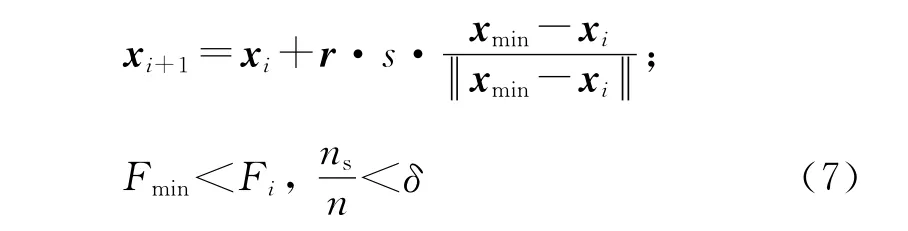
其中xmin代表视野范围内的最优适应度的人工鱼所在位置.当xmin的适应度优于当前xi位置的适应度,并且鱼群不太拥挤时,xi就向最优适应度位置移动.否则,执行觅食行为.
另外,AFS算法设置了公告牌来记录最优状态和当前迭代的最优人工鱼位置信息.
2.2 PSO 算法
PSO 算法是一种广泛用于解决数值优化问题的群智能优化算法.PSO 算法假设解空间内的每个位置为一个粒子,每个粒子具有由被优化函数确定的适应度,同时每个粒子按照一定的搜索规则和较优适应度方向对自身的速度及位置进行调整来求得最优解.PSO 算法的速度和位置更新公式为
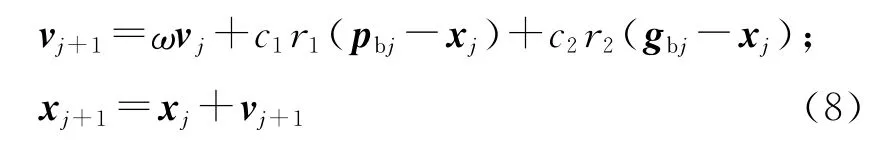
式中:vj为粒子当前速度,vj+1为更新后的粒子速度,ω为 速 度 惯 性 权 重,c1和c2为 加 速 系 数,r1和r2为区间(0,1)内的随机数,xj和xj+1分别为粒子的当前位置和更新后的位置,pbj为粒子当前自身最优位置,gbj为粒子当前全局最优位置.
2.3 PSO 算法公式改进AFS算法
AFS算法初始参数的设置对算法性能有一定的影响.AFS算法的步长因子限制了人工鱼个体的移动步长,如果步长太小就将个体鱼限制在较小搜索空间,增大了寻优时间;如果步长太大,则可能找不到最优值.并且步长因子依赖于人工鱼之间距离的计算,对算法性能影响较大[10-11].
针对上述步长因子对AFS算法性能影响的问题,本文使用PSO 算法公式改进AFS算法,以减小步长因子对AFS 算法性能的影响.AFS 算法中鱼的觅食、聚群和追尾行为的式(5)、(6)和(7)修改为如下新的公式:
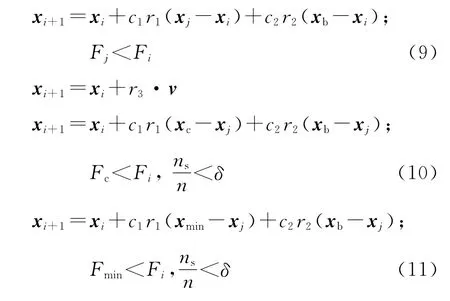
这样AFS算法中的人工鱼个体就可以像PSO算法中的粒子一样,只依赖于视野因子而不依赖于步长因子进行游动行为的选择,寻求最优解.
2.4 混沌机制
混沌(chaotic)是非线性系统中普遍存在的现象,具有确定性和遍历性的特点.在群智能算法中,混沌机制的运用能够提高种群的多样性,进而避免算法出现过早收敛现象,增大搜索到全局最优的性能[7,12].本文选取Logistic映射方法混沌初始化人工鱼群位置,从而寻求SVR 参数全局最优组合.选取的混沌初始化映射方法公式为
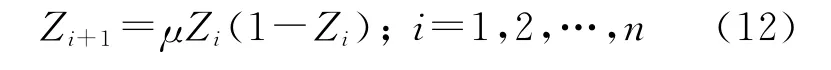
其中μ为控制参数,对系统状态起关键作用.当μ=4时,系统处于完全混沌状态.
2.5 CPSOAFS-SVR模型
本文运用PSO 公式机制优化AFS的混合优化算法优化SVR,建立了混沌粒子群人工鱼群混合优化SVR 的CPSOAFS-SVR 交通流量预测模型.模型具体流程如图1所示.具体实现步骤如下:
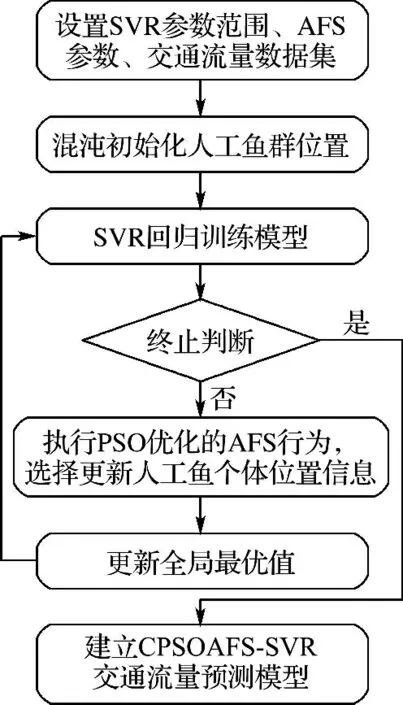
图1 CPSOAFS-SVR 交通流量预测模型Fig.1 CPSOAFS-SVR traffic flow forecasting model
步骤1 数据集设置和参数初始化.将交通流量数据分为训练集和测试集,进行数据预处理.设置SVR 的参数C、ε和σ的取值范围以及PSO和AFS算法的初始参数.混沌初始化人工鱼群位置.
步骤2 计算鱼群的初始适应度.根据训练集训练SVR 模型,选出当前最优并记录初始全局最优的人工鱼的状态,即参数组合(C,ε,σ).
步骤3 人工鱼行为选择.每条人工鱼分别执行混合鱼群算法的觅食、聚群、追尾和随机行为,更新人工鱼个体的位置信息,保存全局最优值以及对应的SVR 参数组合.
步骤4 算法的终止判断.判断是否达到鱼群的最大迭代次数,若不满足则迭代次数加1,跳转至步骤3继续执行;若满足则输出鱼群的最优适应度和最优值对应的SVR 参数组合,建立CPSOAFS-SVR交通流量预测模型,并用于测试集的回归测试,检验测试性能.
3 仿真实验及结果
本文分别采用混沌PSO 优化SVR(CPSOSVR)模型和混沌AFS 优化SVR(CAFS-SVR)模型作为参考模型,进行对比仿真实验.
3.1 数据集准备
本文采用加利福尼亚高速公路性能评估系统(PeMS)采集的实际交通流量数据作为实验数据来源,数据样本时间间隔为5 min.实验选取1d中的早6:00~10:00 的交通流量作为实验数据集.实验数据采用工作日情境下的5个站点数据,每个站点的训练集有576个数据,预测第25d的48个数据.
实验采用历史时间序列的交通流量数据预测未来时刻的交通流量.设xi(t)为路段i上t时刻的交通流量,实验采用前5个时间段的交通流量xi(t-5)、xi(t-4)、xi(t-3)、xi(t-2)和xi(t-1)作为输入,xi(t)作为模型的预测输出[3].
3.2 评价指标和参数设置
为综合比较各模型的仿真实验结果和预测性能,实验采用均方误差ems、平均绝对百分误差emap和均方根误差erms共3个评价指标:


其中yi表示实际值,y*i表示预测值,n为测试样本个数.评价指标值越小,预测性能越好.
实验的初始参数设置如表1所示.混合PSOAFS优化算法中参数与PSO 和AFS算法中的相同.

表1 初始参数设置Tab.1 Initial parameter settings
3.3 实验结果和分析
本实验 利 用libsvm-3.17 Matlab工具箱[13]实现了基于上述各算法优化支持向量回归的交通流量预测模型.表2给出了站点1各个模型下选取的SVR 的参数C、ε和σ的最优组合.

表2 站点1各个模型的参数优化结果Tab.2 Parameter optimization results for each model on site 1
图2显示了站点1 的测试样本在CPSOSVR、CAFS-SVR 和CPSOAFS-SVR模型下的预测值与实际值,表3给出了3个对比模型的评价结果.如图2和表3所示,CPSO-SVR 和CAFS-SVR 模型预测结果相近,而本文提出的CPSOAFS-SVR 模 型 比CPSO-SVR 和CAFSSVR 模型的emap分别减小了8.9%和8.1%,提高了预测精度,证明了CPSOAFS-SVR 模型的准确性.
更一般的,分别对5个站点的数据集进行实验,因为emap最能反映预测性能,所以表4给出了5个站点的emap.结果显示,在不同站点的测试数据集情况下,CPSOAFS-SVR 模型都有最优的预测结果,其emap平均值为4.108%,比CPSO-SVR模型(emap平均值为4.312%)和CAFS-SVR 模型(emap平均值为4.274%)分别 减小了5.0%和4.0%,从而证明了CPSOAFS-SVR 模型的健壮性.
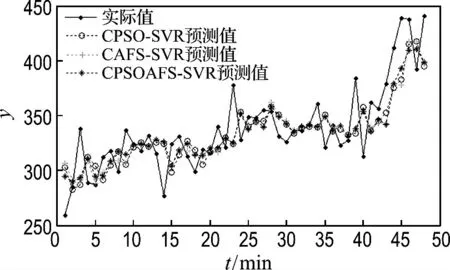
图2 站点1各个模型的实际值与预测值Fig.2 Actual and predicted values for each model on site 1
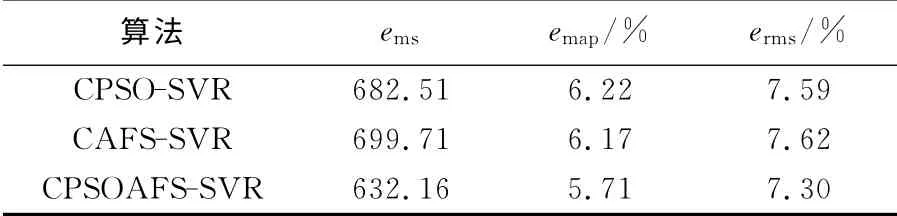
表3 站点1各个模型的评价结果Tab.3 Evaluation results for each model on site 1

表4 5个站点的emap结果对比Tab.4 Comparison of 5sites′emapresults
4 结 语
准确的交通流量预测对交通控制系统是至关重要的,特别是在针对车流高峰期避免碰撞和提高交通效率方面.本文提出将基于混沌初始化机制的混合人工鱼群算法优化SVR 的预测方法,应用到交通流量预测领域来研究模型的可行性.仿真结果表明,提出的CPSOAFS-SVR 交通流量预测模型比单一的PSO 和AFS 优化SVR 模型有更好的预测性能.模型良好的预测结果归功于用PSO 算法减小了AFS 算法中步长因子的影响,从而选出更优的SVR 参数组合,并且混沌初始化机制的运用能够更好地搜索解空间,取得最优预测值.未来将研究一些其他的混合群智能优化算法来更有效地解决交通流量预测问题.
[1] Vlahogianni E I,Karlaftis M G,Golias J C.Shortterm traffic forecasting:Where we are and where we′re going[J].Transportation Research Part C :Emerging Technologies,2014,43:3-19.
[2] 姚智胜,邵春福,高永亮.基于支持向量回归机的交通状态短时预测方法研究[J].北京交通大学学报,2006,30(3):19-22.YAO Zhi-sheng,SHAO Chun-fu,GAO Yongliang.Research on methods of short-term traffic forecasting based on support vector regression[J].Journal of Beijing Jiaotong University,2006,30(3):19-22.(in Chinese)
[3] Castro-Neto M,Jeong Y S,Jeong M K,etal.Online-SVR for short-term traffic flow prediction under typical and atypical traffic conditions [J].Expert Systems with Applications,2009,36(3Part 2):6164-6173.
[4] Smith B L,Williams B M,Keith Oswald R.Comparison of parametric and nonparametric models for traffic flow forecasting [J].Transportation Research Part C:Emerging Technologies,2002,10(4):303-321.
[5] Vlahogianni E I,Karlaftis M G,Golias J C.Optimized and meta-optimized neural networks for short-term traffic flow prediction:A genetic approach[J].Transportation Research Part C :Emerging Technologies,2005,13(3):211-234.
[6] Hong W C,Dong Y,Zheng F,etal.Forecasting urban traffic flow by SVR with continuous ACO[J].Applied Mathematical Modelling,2011,35(3):1282-1291.
[7] Hong W C.Traffic flow forecasting by seasonal SVR with chaotic simulated annealing algorithm[J].Neurocomputing,2011,74(12-13):2096-2107.
[8] Fang N,Zhou J,Zhang R,etal.A hybrid of real coded genetic algorithm and artificial fish swarm algorithm for short-term optimal hydrothermal scheduling[J].International Journal of Electrical Power and Energy Systems,2014,62:617-629.
[9] 姚祥光,周永权,李咏梅.人工鱼群与微粒群混合优化算法[J].计算机应用研究,2010,27(6):2084-2086,2102.YAO Xiang-guang,ZHOU Yong-quan,LI Yongmei.Hybrid algorithm with artificial fish swarm algorithm and PSO [J].Application Research of Computers,2010,27(6):2084-2086,2102.(in Chinese)
[10] 李晓磊.一种新型的智能优化方法——人工鱼群算法[D].杭州:浙江大学,2003.LI Xiao-lei.A new intelligent optimization method—artificial fish school algorithm [D].Hangzhou:Zhejiang University,2003.(in Chinese)
[11] Tsai H C,Lin Y H.Modification of the fish swarm algorithm with particle swarm optimization formulation and communication behavior [J].Applied Soft Computing Journal,2011,11(8):5367-5374.
[12] LI Ming-wei,Hong Wei-chiang,KANG Hai-gui.Urban traffic flow forecasting using Gauss-SVR with cat mapping,cloud model and PSO hybrid algorithm[J].Neurocomputing,2013,99:230-240.
[13] Chang C C,Lin C J.LIBSVM:A library for support vector machines[J].ACM Transactions on Intelligent Systems and Technology,2011,2(3):27.
