轴向行波堆堆芯设计
2015-03-20倪东洋王连杰
孙 伟,李 庆,倪东洋,王连杰
(中国核动力研究设计院 核反应堆系统设计技术重点实验室,四川 成都 610041)
随着能源短缺及环境问题的日益突出,核电在世界能源结构中扮演越来越关键的角色,但核电的大规模发展面临安全、经济、核燃料供应、核废料处理、防止核扩散等挑战[1]。为“一体化”解决制约核电可持续发展的瓶颈问题,国际科学界提出一种新型革命性的反应堆——行波堆[2]。
行波堆基本原理是通过易裂变核素增殖与消耗的动态平衡使反应堆全寿期内反应性保持基本不变[3],核子密度、功率分布形状等物理特性参数也不变,而是以一定的速度在轴向传播或在径向形成“驻波”[4]。因此,行波堆根据堆芯布置方式的不同分为轴向行波堆[3]和径向驻波堆[4]。
本研究主要针对轴向行波堆展开,详细分析轴向行波堆的理论模型,解释公式推导过程中的相关假设,从堆物理的角度论证轴向行波堆概念的可行性。在此基础上开展2 000MW 轴向行波堆堆芯方案设计,分析行波堆堆芯的物理特性。
1 轴向行波堆介绍
1.1 概念介绍
轴向行波堆又称CANDLE堆[1],根本出发点是反应堆燃料的消耗在轴向以一定的速度从一端向另一端推进,在全寿期的任一时刻,不仅反应性基本不变,重要物理特性参数如中子注量率分布、功率分布、核素分布等形状也基本不变,只是以一定的速度在轴向传播。轴向行波堆在运行过程中,堆芯在轴向分为3个区:乏燃料区、主燃烧区、新燃料区。主燃烧区为富集燃料,中子注量率远高于其他两个区,是堆芯主要的能量来源;新燃料区可装载天然铀、贫铀或压水堆乏燃料,在主燃烧区与新燃料区交界位置,高的中子注量率将新燃料区的可裂变核素转化为易裂变核素,随着核素的增殖,主燃烧区以一定的速度向新燃料区移动;在乏燃料区与主燃烧区交界位置,随着主燃烧区易裂变核素的消耗和裂变产物的累积,主燃烧区此处缓慢变为乏燃料区。这样裂变反应将在堆芯内形成“行进的波”(波即中子注量率分布、功率分布、核素分布等的形象表示),其具体燃烧过程如图1所示。
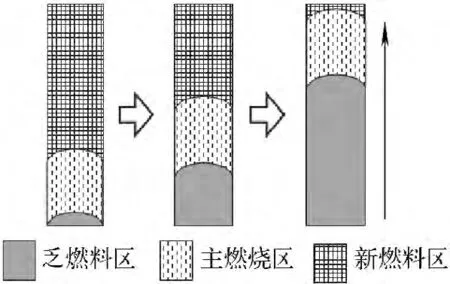
图1 轴向行波堆燃烧过程Fig.1 Burnup process of axial TWR
1.2 理论模型介绍
1996年美国氢弹之父Teller在ICENES上发表了关于轴向行波堆的研究[5],首次设计出U-Th循环长寿命扁长状堆芯。进入21 世纪,法国Hugo Van Dam[6]、日本Sekimoto[7]、乌克兰Fomin[8]和德国卡尔斯鲁厄研究中心的Chen Xue-Nong[9]等都对轴向行波堆的基本原理做了大量详细的研究,其本质都是从中子扩散方程、燃耗方程出发,根据轴向行波堆固有特点做出简化、近似来论证燃烧概念的可行性。具体的公式推导过程如下。
以一维单群计算模型为例,基于反应性反馈的一维单群中子扩散方程,可表达为式(1):
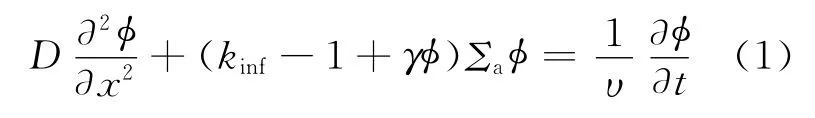
其 中:D 为 扩 散 系 数;φ 为 中 子 注 量 率;x 为 位置变量;kinf为无限介质增殖因数;γ 为反馈系数,通过引入γφ 反馈代替温度反馈,可省去热工水力的分析;Σa为宏观吸收截面;υ为中子飞行速度;t为时间变量。反馈系数的引入使得式(1)成为非线性时间相关的扩散方程。
描述堆物理基本特性的另一重要方程是燃耗方程,主要反映核子密度随时间的变化情况,对扩散方程(1)的影响主要体现在宏观截面上,由燃料无限介质增殖因数kinf的表达式(式(2))可知,kinf正是宏观截面的集中体现,因此可用kinf随燃耗的变化来代替燃耗方程对扩散方程的影响,进而可将燃耗方程与扩散方程组成的非线性方程组化简为单一的非线性扩散方程。代替燃耗方程的kinf表达式如式(3)所示,是中子注量ψ 的二次抛物线形式,式中k0、kmax为燃料初始无限介质增殖因数和燃耗过程中能达到的最大无限介质增殖因数,ψm 为最大无限介质增殖因数kmax时的中子注量。图2示出以U-Zr为燃料,Na为冷却剂的六角形组件kinf随燃耗的变化情况,近似为二次抛物线,这从侧面证明用式(3)代替燃耗方程对扩散方程影响的假设是正确的。

图2 kinf随燃耗的变化Fig.2 kinfversus burnup
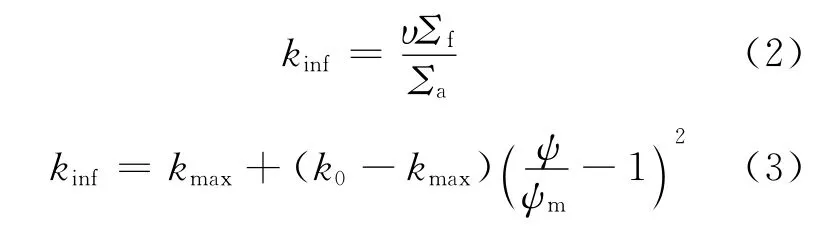
由于轴向行波堆稳定后,重要物理特性参数如核子密度、中子注量率分布、功率分布等在轴向形成稳定的形状,且以一定的速度传播,因此针对中子扩散方程可引入伽利略变化,即:

其中:u为物理特性参数在轴向传播的速度,即行波波速;ξ 为相对于原坐标系以速度u 在轴向运动的新坐标系的变量参数。
由于中子飞行速度υ远大于行波波速,式(1)中中子注量率与时间有关的项相较左端是微小量,可忽略不计,即:
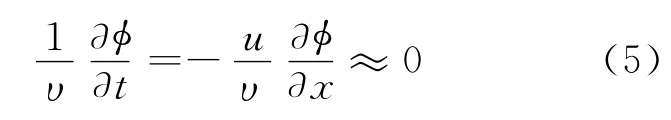
将式(4)、(5)代入式(1)可得:

其中,L0为扩散长度。根据式(3)、(6)可求出中子注量率φ的解:

由于中子注量率非负,因此由式(9)可知轴向行波堆稳定运行的条件为:

式(11)也可作为粗略选取新燃料区燃料的标准,由于本公式推导是在堆芯无泄漏条件下完成的,考虑到实际堆芯有泄漏,因此2kmax+k0值应比3越大越好。
图3示出α取0.056、u 为3cm/a、堆芯高为200cm,燃耗时间为0、10、20、30、40a时式(7)计算值的归一化分布。随着燃耗时间的增加,中子注量率在轴向确实是保持固定的形状以一定的速度移动,这从理论上验证了轴向行波堆概念的可行性。
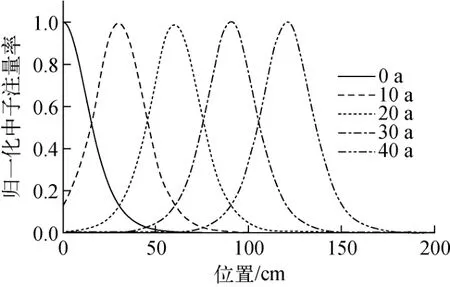
图3 行波形成后堆芯中子注量率随燃耗时间的变化Fig.3 Core neutron fluence rate versus burnup time after wave forming
2 轴向行波堆堆芯设计
2.1 程序介绍
本文所用程序为HANDF-E 程序包[10]。HANDF-E主要包括组件程序KYLIN-1、六角形节块法堆芯程序HANDF和组件堆芯连接程序HLINK,具备宏观燃耗计算和功率重构功能。HANDF-E程序包的详细介绍见文献[10]。
2.2 堆芯方案设计
轴向行波堆堆芯寿期设计为60a,组件几何参数列于表1。图4示出堆芯燃料轴向分区方式和新燃料区径向简图。为能充分利用现有Na工艺的经验,更快地工程化应用,所设计堆芯选用Na为冷却剂。金属燃料U-Pu-Zr相较其他燃料更有利于轴向行波堆堆芯长寿期设计,因此堆芯设计时燃料选择U-Pu-Zr,且为提高燃料合金的熔点,相应Zr含量取为10%,即燃料为U-Pu-10%Zr,密度为11.925g/cm3。包壳材料为HT-9钢,密度为7.98g/cm3。

表1 行波堆组件参数Table 1 Parameters of TWR assembly
轴向行波堆堆芯设计时启堆区设计是其难点,为实现反应性波动小、轴向功率分布形状等不变的目标,启堆区设计时考虑如下几种情况。
1)启堆区长度选取
简单启堆区设计时轴向功率分布示于图5。由图5可知,轴向行波堆稳定后,功率分布的跨度约为320cm,为保证启堆初的功率分布形状与稳定时的一致,启堆区设计时启堆区长度也由轴向行波堆稳定运行时主燃烧区的长度来确定,使两者大小基本相同。主燃烧区是主要的能量来源,长度相同的设计是保持重要物性参数在轴向形状不变的条件之一。

图4 轴向行波堆燃料分区布置(a)及径向简图(b)Fig.4 Fuel distribution chart of axial TWR(a)and radial diagram of axial TWR at fresh fuel area(b)
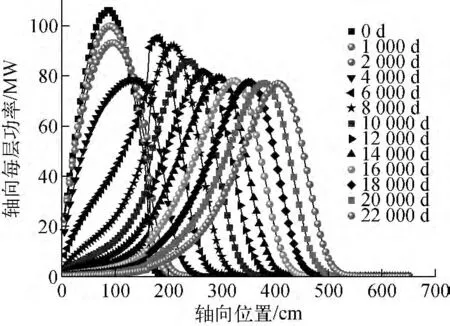
图5 简单启堆区设计时轴向功率分布Fig.5 Distribution of axial power at simple startup area design
2)启堆区轴向分段设计
启堆区燃料轴向分段设计是保持重要物理特性参数在轴向形状不变的另一重要条件。轴向行波堆稳定运行后,主燃烧区轴向各段燃料成分不同,增殖性能也不同,寿期初启堆区设计时只有燃料轴向分段布置时才能模拟行波堆稳定运行后的特性。在启堆区长度确定的情况下,轴向段数越少越好。本文中选取5cm 为一轴向段,5cm 每段既能保证轴向各段功率相差较小,又可作为后期轴向卸换料的一个最小单元,便于燃料管理。
3)启堆区轴向各段核子密度选取
轴向行波堆稳定运行后,主燃烧区轴向各段燃料成分相当复杂,包括可裂变核素、易裂变核素、裂变产物等,尤其是裂变产物由于其种类、含量的不同对堆芯反应性、功率分布影响巨大。启堆区设计时应尽可能采用少的核素来模拟轴向行波堆稳定后主燃烧区大量核素的特性,初始核素成分越少制造越简单,成本越低。本 文 选 取235U、239Pu、241Pu 来 模 拟 稳 定 后 易 裂变 核素 的 作 用,选 取238U、238Pu、240Pu、242Pu 来模拟可裂变核素的作用,选取吸收截面较大的核素93Nb来模拟裂变产物的作用。其中238Pu、239Pu、240Pu、241Pu、242Pu的比例参考工业钚,这样设计的好处是可将压水堆等其他堆乏燃料中的Pu直接用于轴向行波堆,利于核燃料的充分利用,提高经济性。
启堆区轴向各段核子密度的比例也有一定要求,由图5可知,行波堆稳定后主燃烧区功率分布大致分两段,功率峰左端至乏燃料区为功率下降段,右端至新燃料区为功率上升段,下降段明显较上升段长,比例约为2∶1。为更好地模拟轴向各段功率变化情况,真实反映主燃烧区各段功率变化趋势,功率下降段组件kinf随燃耗变化的趋势也应是逐渐减小的,功率上升段应是先增大后减小的,各段具体尺寸参考稳定后的比例2∶1来界定。图6示出启堆区轴向各段具体的核素密度。

图6 启堆区核素密度分布Fig.6 Nuclide density distribution at startup area
4)新燃料区径向分区布置
堆芯中央布置235U 富集度为0.25%的贫铀,径向外区布置235U 富集度为1.5%的铀。新燃料区中央富集度低、外区富集度高的布置方式,一方面有利于展平径向功率分布,提高堆芯的安全性、经济性,另一方面相较全部使用贫铀而言,适当布置部分高富集度燃料可给堆芯提供一个正的反应性,在新燃料区易裂变核素增殖引入的正反应性小于主燃烧区易裂变核素消耗引入的负反应性时,可保持堆芯始终处于临界点附近。
2.3 计算结果
图7示出轴向行波堆堆芯寿期内60a堆芯keff随燃耗的变化,keff的波动范围约为0.5%,寿期内较小的剩余反应性既利于控制,又确保了堆芯安全。
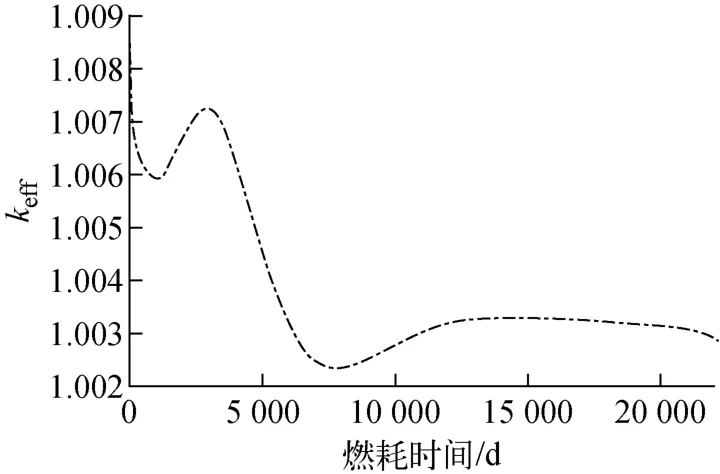
图7 堆芯keff随燃耗时间的变化Fig.7 keffof core versus burnup time
图8示出轴向行波堆堆芯寿期内功率分布。由图8可见,轴向功率分布形状基本保持不变(最大层的相对偏差为8.1%),而是以约5.5cm/a的速度在轴向传播。寿期内最大线功率密度为58.701kW/m,出现在中央组件节块处。
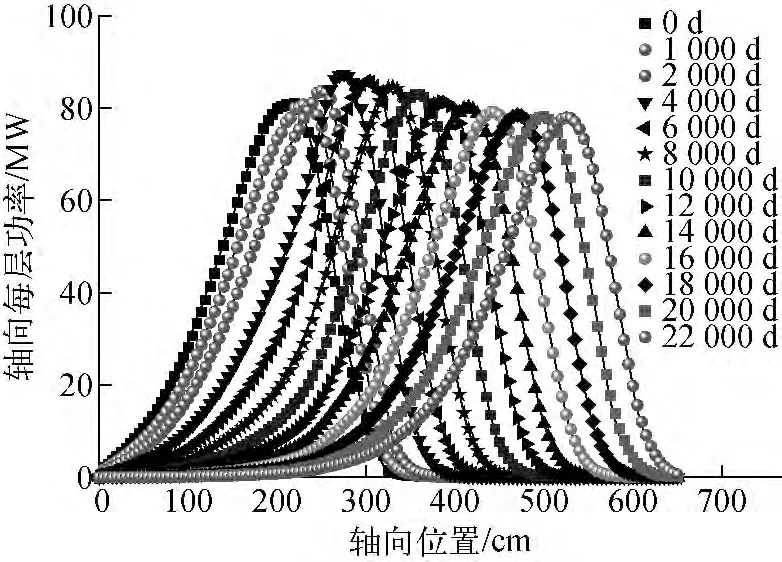
图8 轴向行波堆寿期内功率分布随燃耗的变化Fig.8 Power distribution of axial TWR versus burnup in whole life
轴向行波堆堆芯寿期末组件燃耗深度列于表2(组件位置编号示于图4b)。由表2可知,轴向行波堆堆芯寿期末最大燃耗深度为584GW·d/tHM,处在堆芯中央位置;而在初始堆芯前端,由于燃料含量少,泄漏高,燃耗深度较低,为14.2GW·d/tHM;在增殖区末端,由于处于行波的波前位置,属于燃耗积累初期,燃耗最浅。
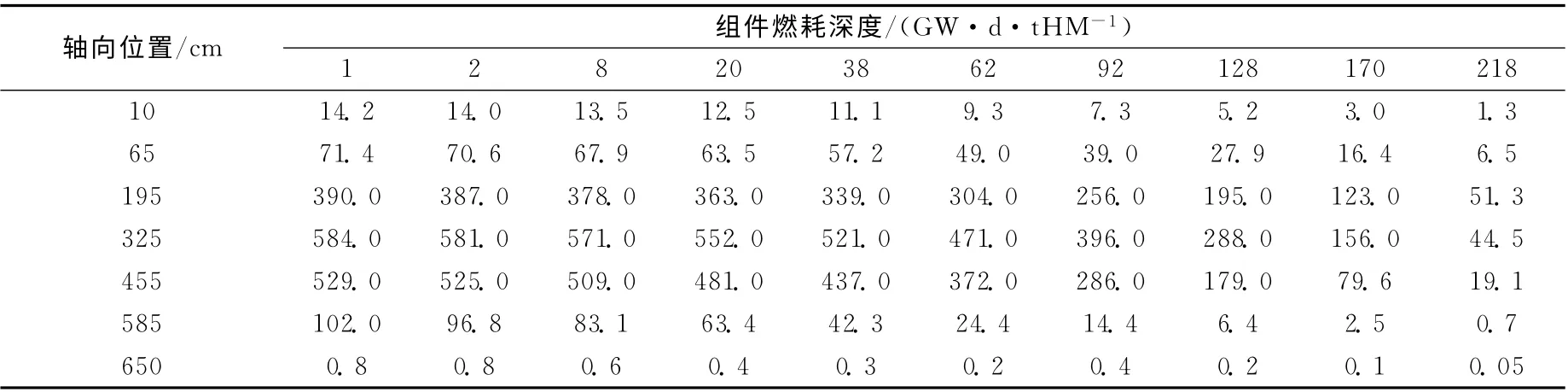
表2 轴向行波堆堆芯寿期末组件燃耗深度Table 2 Assembly burnup depth of axial TWR at end life
图9 示出寿期初及20、40、60a时堆芯径向节块功率分布(径向组件位置是从堆芯中央向外围的一个编号)。由图9 可知,随着燃耗的加深功率分布形状会以一定的速度在轴向移动,但会产生径向上的一个“扭曲”,即向传播相反方向弯曲,这主要是因为轴向行波堆径向不同位置处功率分布形状等物性参数在轴向的传播速度不一致引起的。行波的形成与材料燃耗水平密切相关,随着燃耗时间的推移,必然导致空间上燃耗深度的不均匀性,即会在径向上产生不均匀的非线性特征。
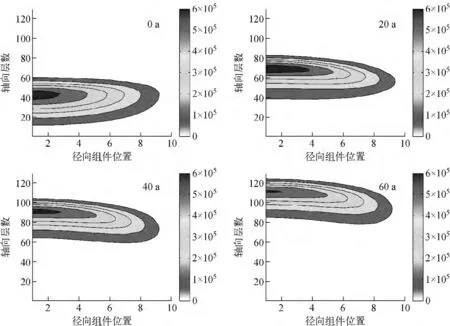
图9 堆芯功率分布Fig.9 Power distribution of core
3 结论
本文从中子扩散方程、燃耗方程出发,针对轴向行波堆稳定后功率分布保持一定形状不变而以一定速度在轴向传播的特性,引入伽利略变换,经公式推导求解得到行波稳定后的孤立波解。并针对公式推导中的相关假设从堆物理的角度进行解释,从理论层面论证了轴向行波堆概念的可行性。
在理论模型论证的基础上,设计出2 000MW轴向行波堆堆芯,并针对轴向行波堆启堆区设计进行了重点研究,通过采用合适的启堆区长度、燃料成分和富集度轴向分区设计,有效地实现了全寿期内反应性基本不变、中子注量率分布形状等也不变而是以一定的速度在轴向传播的目标。
[1] A technology roadmap for generationⅣnuclear energy systems,GIF-002-00[R].U.S.:DOE Nuclear Energy Research Advisory Committee and the GenerationⅣInternational Forum,2002.
[2] SEKIMOTO H,RYU K.CANDLE:The new burn-up strategy[J].Nucl Sci Eng,2001,139:306-317.
[3] SEKIMOTO H,NAGATA A. “CANDLE”burnup regime after LWR regime[J].Progress in Nuclear Energy,2008,50:109-113.
[4] JOHN G.Traveling wave reactor technology development and deployment[R].USA:Terra-Power company,2010.
[5] TELLER E,ISHIKAWA M,WOOD L.Completely automated nuclear reactors for long-term operation[R].Obhinsk,Russia:[s.n.],1996.
[6] DAM H V.Flux distributions in stable criticality waves[J].Ann Nucl Energy,2003,30:1 495-1 504.
[7] SEKIMOTO H,RYU K.A long life lead-bismuth cooled reactor with CANDLE burnup[R].Japan:Tokyo Institute of Technology,2000.
[8] FOMIN S,MELNIK Y,PILIPENKO V,et al.Initiation and propagation of nuclear burning wave in fast reactor[J].Progress in Nuclear Energy,2008,50:163-169.
[9] CHEN Xue-Nong, KIEFHABER E, MASCHEK W.Fundamental burn-up mode in a pebble-bed type reactor[J].Progress in Nuclear Energy,2008,50:219-224.
[10]孙伟.行波堆堆芯设计程序功能研发报告,TWRRK-410000-BG1[R].成都:中国核动力研究设计院,2012.
