氟盐冷却球床堆球栅元少群截面计算

戴 明，朱贵凤，戴 叶，于世和，邹 杨，3，余笑寒，3

（1.中国科学院 上海应用物理研究所，上海 201800；2.中国科学院大学，北京 100049；3.中国科学院 核辐射与核能技术重点实验室，上海 201800）

氟盐冷却球床堆（PB-FHR）经10余年的发展，已逐步由预概念设计走向试验堆基准设计。2012年美国能源部（DOE）启动合作研究项目（IRP）研究先进高温堆（AHTR）［1］的发展技术路线，包括进行实验堆、原型堆和商业堆的设计以及关键技术、策略需求分析，在该项目中AHTR被命名为氟盐冷却高温堆（FHR），并选用PBFHR（氟盐冷却球床堆）作为设计基准［2］。中国科学院自2011年开始启动实施“未来先进核裂变能”战略性先导科技专项，进行钍基熔盐堆核能系统的研究（专项简称TMSR），PB-FHR选为该专项试验堆基准设计方案之一。

PB-FHR 中子学求解与传统压水堆方法相比存在一些差异，如栅元能谱计算要考虑双重非均匀性及堆芯不同位置泄漏反馈影响［3］，流动球床燃耗计算时谱区内不同批次燃料同时存在且认为具有一致的有效微观截面［4］等。PB-FHR的少群截面计算是其堆芯扩散计算分析的重要研究前提，它将对扩散计算的准确性产生重大影响。球床堆复杂的几何模型构成所谓的双重非均匀性系统，第1重非均匀性为燃料核和包覆层及石墨基质，第2重非均匀性为燃料区、球石墨壳和氟盐冷却剂。双重非均匀性要求能准确求解可分辨共振区的共振吸收［5］。对于可分辨共振能区一般采用求解基于碰撞概率法的精细群慢化方程，在ZUT 共振处理软件中，采用解析的数值积分精确求解相关碰撞概率［4］，燃料核逃脱概率与燃料核的总截面相关，而该截面在共振区又随能量改变很大，所以采用精细群求解。SRAC 的共振处理程序PEACO 能调用共振区点连续截面MCROSS库直接求解基于碰撞概率法的精细群慢化方程。对于双重非均匀性的处理，可采用类似于SCALE 处理双重非均匀栅元的CSAS［6］的共振计算两步法，即先计算包覆颗粒共振能区空间均匀化有效微观共振截面，再利用该有效截面进行燃料球栅元计算。庄坤等［7］使用SRAC 采用该两步法与MVP-BURN 程序比较了燃料球有效增殖因数随燃耗的变化。SRAC也提供直接一步处理双重非均匀性的功能，相关碰撞概率的求解没有ZUT 精确，而是采用了一些假设。该方法与两步法无本质区别。

本工作通过与采用连续能量蒙特卡罗软件MCNP计算的参考模型对比，分析确定论软件SRAC对于准确加工PB-FHR少群截面的适用性。主要比较参量有无穷增殖因数（Kinf），少群均匀化总截面、俘获截面和裂变截面。计算包括两个温度点：冷态（300K）和热态（1 000K）。

1 计算程序及方法

1.1 确定论软件

确定论软件SRAC［8］是针对各种热中子堆的中子学计算而设计的，能加工有效微观和宏观群截面，进行静态栅元和堆芯计算，能提供堆芯设计或实验分析所需的相关关键参数。公用数据库为基于JENDL-3.3库加工的超过300种核素的多群库。SRAC 的共振处理程序PEACO 采用基于碰撞概率法直接求解共振能区超精细群慢化方程，能很好地处理PB-FHR的球型燃料元件所构成的双重非均匀系统。

本文主要采用SRAC的碰撞概率程序PIJ进行通量计算，采用固定源模式。选择HOMOSP程序求零几何曲率下全能群B1方程解，并给出无穷增殖因数和均匀化能谱。可分辨共振区采用PEACO 处理，处理能区为快热分界能到961.12eV，勒宽间隔为0.000 5，两区微观栅元碰撞率比采用透射截面模型。

1.2 MCNP程序

MCNP程序［9］是由美国洛斯阿拉莫斯国家实验室开发的一个通用的蒙特卡罗程序。MCNP程序采用连续点截面库，具有强大的几何处理能力，在核能新堆型的设计上发挥着很大作用。MCNP 通过使用各种记数卡统计大量粒子在介质中发生的输运事件来给出宏观结果。本文中，PB-FHR 的燃料与熔盐等材料温度非常高，运用NJOY 程序为MCNP 中涉及的材料做了相应的温度库以使计算结果更加精准。

MCNP在本文中主要是对球栅元内各种反应率和通量分别采用FMn卡和Fn 进行统计，两者相除即为所需的少群截面［10］。为方便与SRAC比较，给出的能谱为107群能谱。由于MCNP未提供统计出射中子能量及方向信息的计数卡［11］，不能直接求得散射矩阵及平均散射余弦，所以散射矩阵和扩散系数未给出相应结果。为统计所有包覆颗粒（TRISO）的燃料核的总体积，采用VOID 卡、SDEF 卡和F4卡统计燃料核总体积［9］。

1.3 计算模型

参考VSOP及MICROX-2软件对球床模块高温气冷堆（PBMR）球燃料元件建模［12］，PB-FHR 球栅元等效几何模型如图1所示，包层冷却剂的厚度取决于包覆颗粒填充因子。MCNP建模时弥散的TRISO 采用简立方栅格排布于燃料区，燃料球结构也采用图1模型。少群常数能群划分参考文献［13］给出的石墨慢化堆推荐的8 群划分方法，取与其相邻的SRAC的多群库能群分界能（表1）。相关模型参数列于表2。

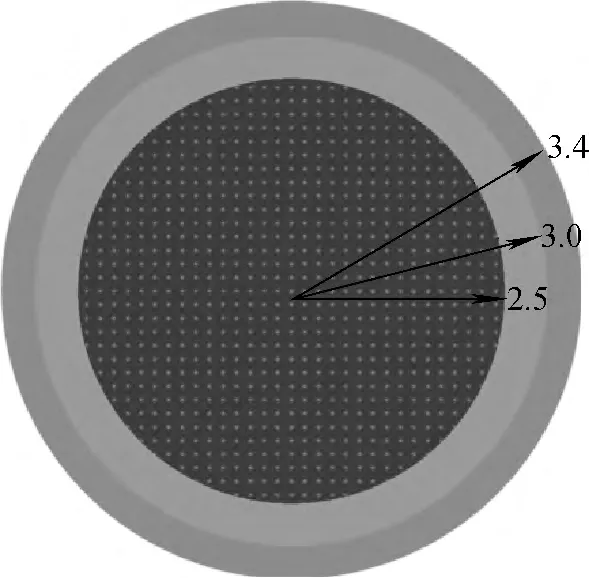
图1 PB-FHR球栅元模型Fig.1 Pebble model of PB-FHR

2 结果与讨论

2.1 无穷增殖因数与少群截面计算

PB-FHR球栅元无穷增殖因数与少群截面在冷态的计算结果列于表3。除2群的俘获截面和1群的裂变截面外，各截面的相对偏差在1.45%以下，特别是包括可分辨共振能区的3群的俘获截面相对偏差仅为0.04%。SRAC计算得到的2群的俘获截面较MCNP计算得到的大12.76%，SRAC计算得到的1群的裂变截面较MCNP计算得到的小7.08%。SRAC计算的无穷增殖因数与MCNP计算的相比大0.05%。

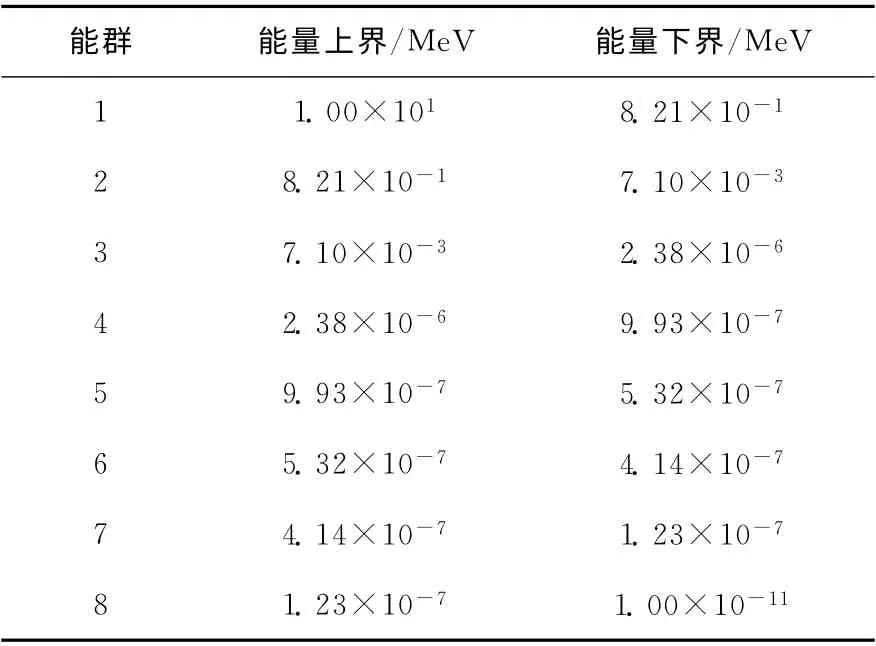
表1 少群常数能群划分Table 1 8-group structure

表2 PB-FHR球栅元主要参数Table 2 Parameters of lattice of PB-FHR

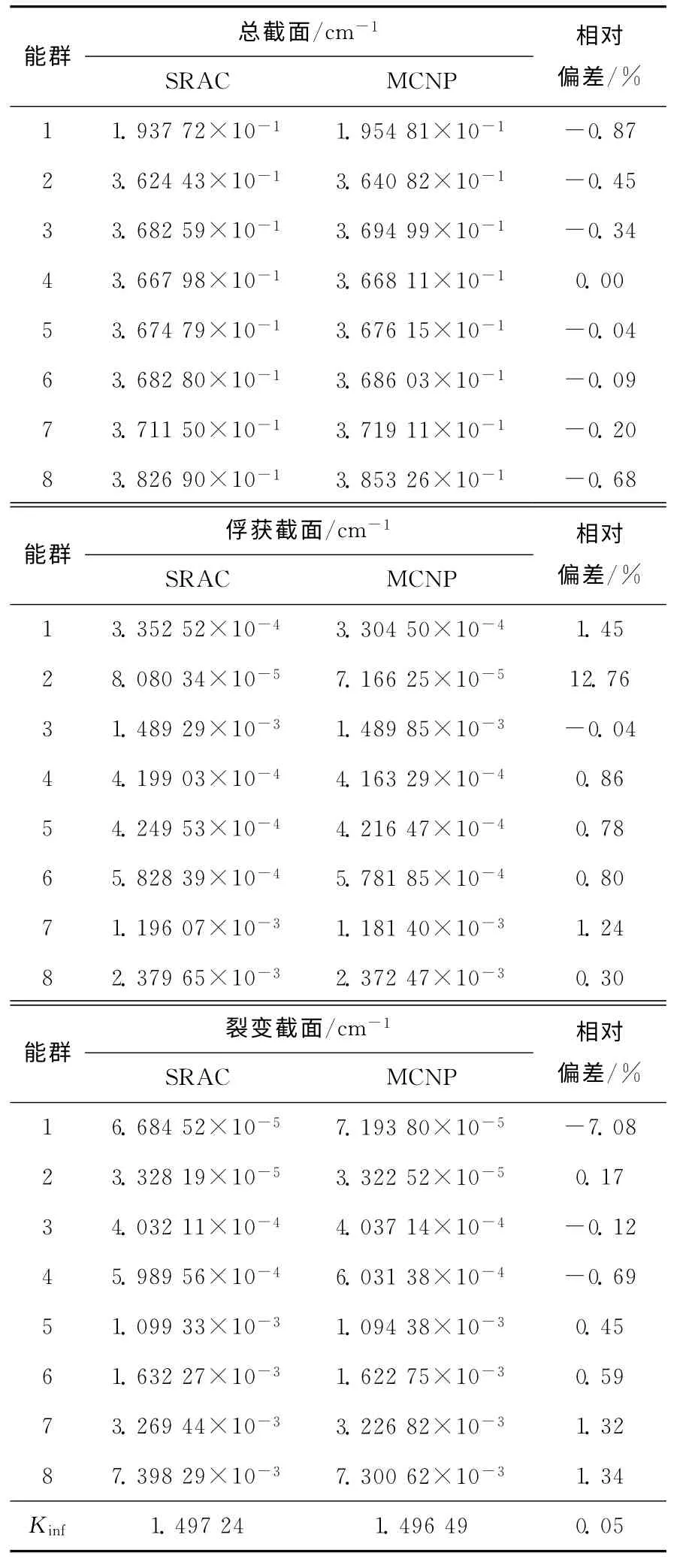
表3 冷态时SRAC计算的少群截面及无穷增殖因数与MCNP结果比较Table 3 Few-group cross sections and infinite multiplication factors comparison at 300K

表4 所列为PB-FHR 球栅元无穷增殖因数与少群截面在热态的计算结果。除2群的俘获截面和1群的裂变截面外，各截面的相对偏差在2.25%以下，3群的俘获截面相对偏差仅为0.08%。SRAC 计算得到的2 群的俘获截面较MCNP计算得到的大12.74%，SRAC 计算得到的1群的裂变截面较MCNP 计算得到的小7.07%。SRAC 计算的无穷增殖因数与MCNP计算的相比大0.04%。可看出，温度的改变对两个计算的影响是一致的，计算结果的差异未扩大。SRAC计算的球栅元的无穷增殖因数和少群截面与MCNP 结果基本符合，说明SRAC处理PB-FHR 球栅元双重非均匀性的方法基本可取。

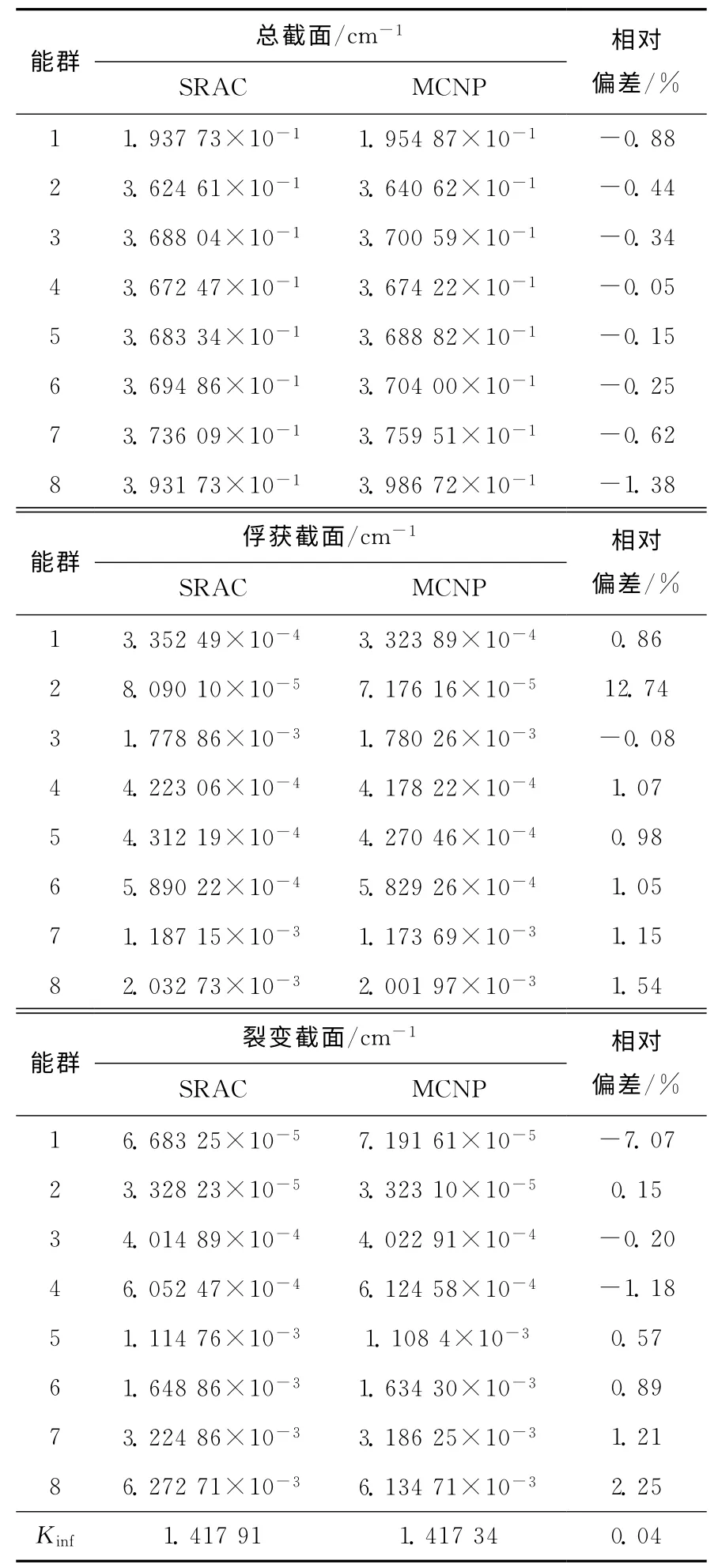
表4 热态时SRAC计算的少群截面及无穷增殖因数与MCNP结果比较Table 4 Few-group cross sections and infinite multiplication factors comparison at 1 000K

2.2 FLiBe熔盐

表5列出热态下FLiBe熔盐对1、2群俘获截面的影响。当计算模型中无FLiBe熔盐时，可看到2群的俘获截面相对偏差由12.74%降低到1.54%，当把熔盐中的F元素由C元素替代后，2群的俘获截面相对偏差也降为1.08%。说明SRAC对于FLiBe熔盐中的F 元素处理不当是造成2 群俘获截面相对偏差较大的原因。熔盐FLiBe中的F 元素为中等质量核素，相关共振能区位于平滑能量区（67.4keV～0.82 MeV），对应于少群能群结构中的2群，相关截面在该能区也较其他轻核的高出1 个量级，且共振峰更宽。SRAC 带屏蔽因子的Bondarenko类型截面库构建时采用窄共振近似，该近似得到的用于并群的能谱能有效适用于重质量核素，但对于在高能区有共振结构的轻中等质量核素不太精确。SRAC对F元素采用该近似就造成F 元素共振区的多群截面上有偏差。同样，SRAC 对轻核（如C、O、Li和Be）的俘获处理也不理想，这造成了表5 中无FLiBe熔盐时1 群俘获截面相对偏差达到23.98%，同样造成了熔盐中的F由C代替时1群俘获截面相对偏差达到3.67%。

2.3 TRISO 尺寸

SRAC处理双重非均匀性时，对于非PEACO处理能区（热区及快区E＞961.12eV），燃料区核素浓度由带石墨基质的TRISO 栅元体积权重均匀化得到。图2所示为TRISO几何按表2中原始尺寸等比例变化后热态下的无穷增殖因数、3群俘获截面、1群裂变截面及8群裂变截面的计算结果。等比例变化保证燃料区材料体积权重均匀化后核素原子浓度不变，但相应的TRISO 尺寸改变为表2计算模型的0.1～2.5倍。零倍时即完全均匀分布，无双重非均匀性效应。为考虑MCNP建模中的切球影响，采用MCNP软件以2.5cm 半径的60 000 000粒子平面中子源及F4 卡统计了所有TRISO 的燃料核的总体积。

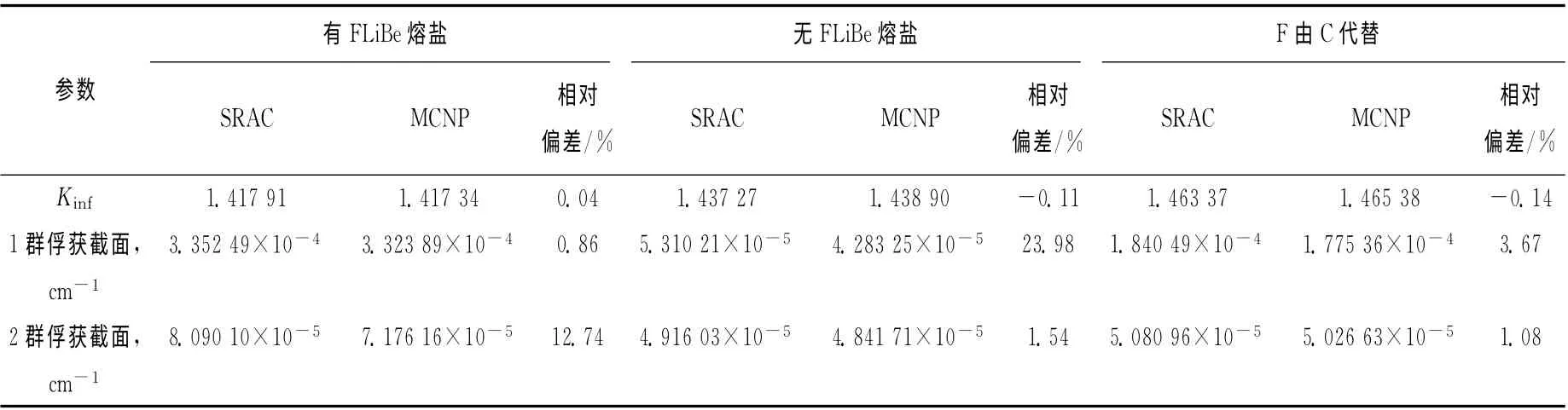
表5 热态下FLiBe对俘获截面的影响Table 5 Effect of FLiBe salt on cell-homogenized capture cross section at 1 000K

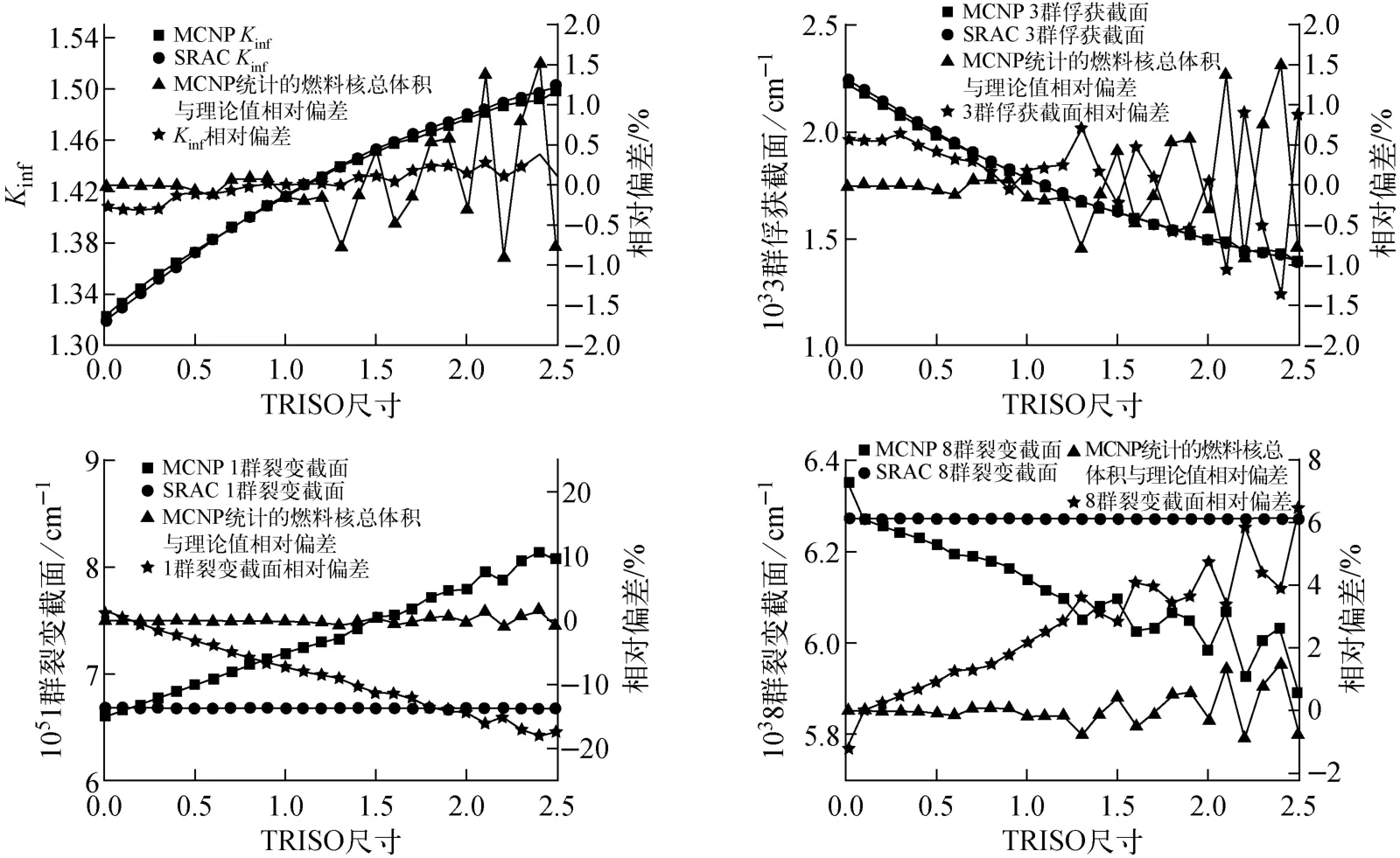
图2 热态下填充比10%时不同TRISO 大小对结果的影响Fig.2 Effects of TRISO size on results at 10% TRISO packing factor at 1 000K

TRISO 尺寸由零倍（无双重非均匀性）增加至2.5倍的过程能很好体现双重非均匀性对于PB-FHR 栅元计算的影响。由图2 可知，TRISO 尺寸越大，含可分辨共振区的3群的俘获截面越小，无穷增殖因数越大，2.5倍尺寸时无穷增殖因数较无双重非均匀性时偏大约15%，其3群俘获截面较无双重非均匀性时偏小约40%，说明双重非均匀性效应对于PB-FHR球栅元计算影响很大。同时，SRAC 计算的无穷增殖因数与MCNP结果相比吻合很好，说明SRAC对双重非均匀性的处理方法在TRISO尺寸改变时也能很好适用。图2中，无穷增殖因数和3群俘获截面的偏差随TRISO 尺寸的波动与MCNP模型中燃料核总体积与理论值的偏差随TRISO 尺寸的波动规律一致或相反，说明MCNP 模型在TRISO 尺寸较大时切球会对结果产生一定影响。

如图2所示，SRAC 计算的1群和8群的裂变截面不会随TRISO 尺寸变化，与零倍尺寸的结果相同，这是由于SRAC对于非PEACO 处理能区（热区及快区E＞961.12eV）的计算模型为未考虑双重非均匀性的体积权重均匀化的模型，即图2中的零倍尺寸。由MCNP的计算结果可看到，当TRISO 尺寸增大时，1 群的裂变截面偏差最大时约偏小17%，8群的裂变截面最大相对偏差约6.5%，MCNP 计算结果随TRISO 尺寸的波动与其模型中燃料核总体积与理论值的偏差波动规律一致。1群裂变截面会随TRISO 尺寸增大而增大，这是由于TRISO 燃料核尺寸增大时，产生于燃料核内的裂变中子逃脱燃料核的概率变小，重核与慢化轻核比例没有改变，导致裂变中子与慢化轻核碰撞而慢化到其他群的概率降低，裂变中子与重核的碰撞概率增大，1群的裂变截面将增大。8群裂变截面会随TRISO 尺寸增大而降低是因为由轻核慢化的热中子进入到TRISO 燃料核会有空间自屏，尺寸越大空间自屏效应越明显。所以，1群和8群裂变截面会有较大偏差的原因为SRAC在非PEACO 处理能区未考虑双重非均匀性效应。

3 结语

本文采用确定论软件SRAC计算了PB-FHR球栅元的无穷增殖因数，少群均匀化总截面、俘获截面和裂变截面，并使用连续能量蒙特卡罗软件MCNP 验证与分析。SRAC 计算的球栅元的无穷增殖因数和少群截面与MCNP 结果基本符合，说明SRAC处理PB-FHR 球栅元双重非均匀性的方法基本可取。SRAC快群数据库对FLiBe熔盐中的F 元素共振处理不理想，造成2群俘获截面偏差较大。TRISO 尺寸变化的计算结果说明双重非均匀性对于PB-FHR球栅元有很大影响，且1群和8群裂变截面会有较大偏差的原因为SRAC在非PEACO 处理能区未考虑双重非均匀性效应。结果表明：SRAC程序计算结果与MCNP吻合，其适用于对PB-FHR 进行少群截面加工。

［1］ FORSBERG C W，PETERSON P F，PICKARD P S.Molten-salt-cooled advanced high-temperature reactor for production of hydrogen and electricity［J］.Nuclear Technology，2003，144（1）：289-302.

［2］ FORSBERG C，PETERSON P F，SRIDHARAN K.Fluoride-salt-cooled high-temperature reactors（FHRs）for base-load and peak electricity，grid stabilization，and process heat［R］.Boston： Massachusetts Institute of Technology，2013.

［3］ HUDSON N H，OUGOUAG A M，RAHNEMA F，et al.A pebble bed reactor cross section methodology［J］.Annals of Nuclear Energy，2009，36（1）：1 138-1 150.

［4］ RÜTTEN H J，HAAS K A.V S O P（99／05）computer code system for reactor physics and fuel cycle simulation［R］.Jülich：Forschungszentrum Jülich，2005.

［5］ BENDE E E，HOGENBIRK A H.Analytical calculation of the average dancoff factor for a fuel kernel in a pebble bed high-temperature reactor［J］.Nuclear Science and Engineering，1999，133（1）：147-162.

［6］ GOLUOGLU S，LANDERS N F，PETRIE L M，et al.CSAS：Control module for enhanced criticality safety analysis sequences［R］.Oak Ridge：Oak Ridge National Laboratory，2006.

［7］ 庄坤，曹良志，吴宏春，等.球床型固体燃料熔盐堆计算软件开发［J］.原子能科学技术，2013，47（增刊）：463-466.ZHUANG Kun，CAO Liangzhi， WU Hongchun，et al.Software development for pebble bed MSR calculation［J］.Atomic Energy Science and Technology，2013，47（Suppl.）：463-466（in Chinese）.

［8］ OKUMURA K，KUGO T，KANEKO K，et al.SRAC2006：A comprehensive neutronics calculation code system［R］.Ibarakiken：Japan Atomic Energy Agency，2007.

［9］ X-5 Monte Carlo Team.A general Monte Carlo N-particle transport code，Version 5［R］.Los Alamos： Los Alamos National Laboratory，2003.

［10］李满仓，王侃，姚栋.基于连续能量蒙特卡罗方法的均匀化群常数计算［J］.核科学与工程，2012，32（4）：306-314.LI Mancang，WANG Kan，YAO Dong.Continuous energy Monte Carlo method based homogenization multi-group constants calculation［J］.Chinese Journal of Nuclear Science and Engineering，2012，32（4）：306-314（in Chinese）.

［11］ILAS G，RAHNEMA F.A Monte Carlo based nodal diffusion model for criticality analysis of spent fuel storage lattices［J］.Annals of Nuclear Energy，2003，30（1）：1 089-1 108.

［12］REITSMA F，STRYDOM G，DE HAAS J B M，et al.The PBMR steady-state and coupled kinetics core thermal-hydraulics benchmark test problems［J］.Nuclear Engineering and Design，2006，236（1）：657-668.

［13］MPHAHLELEA R， OUGOUAGB A M，IVANOV K N，et al.Spectral zone selection methodology for pebble bed reactors［J］.Annals of Nuclear Energy，2011，38（1）：80-87.