压缩域直扩测控通信信号载波同步技术*

程艳合，杨文革，屈文星，张益东

(解放军装备学院 光电装备系，北京101416)

1 引 言

扩频体制具有隐蔽性、抗干扰和抗截获等优点，因此在航天测控通信领域受到了广泛重视，目前统一扩频测控通信系统已经实现工程化。虽然现行统一扩频测控系统具备一定的电子对抗能力，但在日趋复杂的空间信息对抗环境下，依然面临着严重的安全威胁，表现出信息保密性能和抗干扰能力的不足［1］。

随着抗干扰技术不断发展，提高扩频码率、发展宽带甚至超宽带扩频测控通信系统是未来发展的一个重要趋势。然而，高扩频码率意味着信号带宽的宽带甚至超宽带化，会给接收机前端模数转换器(Analog－ to－ Digital Converter，ADC)提出极高要求，尤其是针对超宽带直扩测控通信信号而言，接收系统的采样成本、设计难度和实现复杂度都会急剧增加［2］，甚至导致在卫星、火箭等空间资源有限平台上的超宽带系统可能会根本无法实现。另外，即使接收系统能够以经典采样理论实现超宽带信号采集，所获得信号数据率也会非常高，高数据率会给信号存储、传输、捕获跟踪与数据解调等处理带来沉重压力。

近年来，出现了一种称为压缩感知(Compressed Sensing，CS)的全新信息获取理论，在该理论框架下，采样速率不再取决于信号带宽，而是由信号所包含信息量决定，可以有效降低采样率和数据率，这为降低信号采集成本和缓解同步解调处理压力提供一个崭新的思路［3］。目前，压缩感知在扩频有关方面已经取得一些研究成果。文献［4］根据GPS 信号相关稀疏性，基于多通道压缩采样框架提出了一种新型信号捕获方法，可以减少所需相关器数量。文献［5］针对扩频通信信号，提出了一种基于压缩感知的信号采集和恢复方法，并仿真验证了其可行性，但未考虑载波和噪声。文献［6］通过构造稀疏基字典对直扩测控通信信号进行稀疏性分析，初步探讨了该类型信号压缩感知相关问题。这些成果都不可避免地要进行信号重构处理，而重构算法计算复杂度偏高，需要消耗大量的计算资源［7］。测控通信系统的处理目标是信号流，其计算复杂度和实时性是首要考虑因素。因此，传统压缩感知重构算法并不适用于大多数的实时处理系统。

扩频测控通信系统要实现测速、测距和信号解调，必须进行载波和伪码同步。传统锁相环与延时锁定环能够完成载波和伪码相位跟踪，但是压缩采样后的压缩域数字信号无论在时域还是频域来看已不再是传统数字信号，传统跟踪环路对其不再适用。本文通过压缩域信号估计理论分析，首先构建了一种压缩域直扩测控通信信号处理框架，然后对其中的载波同步方法展开了深入分析，提出了一种压缩域Costas 环路，理论分析和仿真结果验证了所提出环路的有效性，表明其能够实现压缩域信号载波跟踪和解调等功能。

2 基于CS 的直扩测控通信信号处理框架

2.1 压缩域信号处理

一般认为压缩感知理论框架主要包括三个核心问题，即信号稀疏性、压缩测量、信号重构。在压缩感知应用过程中通常需要首先重构出原信号，然后再利用传统算法对信号进行处理，如图1(a)所示，这种压缩感知处理思路虽然能够降低信号采样率，但由于信号重构复杂度很高，会消耗大量计算资源，而且在大多数情况下，我们感兴趣的并不是原信号，而是信号中所包含的信息。

根据文献［8］给出的压缩域信号估计理论分析，压缩采样没有破坏原信号之间存在的结构差异，因此原信号之间的相关运算可由其压缩采样值的相关运算处理来直接等效替代，无需先重构原信号再进行相关运算。基于此研究结论，本文采用压缩域信号处理来替代基于信号重构的处理思路，如图1(b)所示，在压缩采样后不再进行信号重构，而是在压缩域直接获取所感兴趣信息。

图1 压缩感知处理框架Fig.1 Compressed sensing processing framework

2.2 压缩域直扩测控通信信号处理框架

在文献［6］对DS TT＆C 信号稀疏性研究的基础之上，图2给出了基于压缩感知的直扩测控通信信号处理框架。

图2 基于CS 的直扩测控通信信号处理框架Fig.2 DS TT＆C and communication signal processing framework based on compressed sensing

由图2可知，信号处理系统主要包括射频接收模块、压缩采样模块和压缩域信号处理模块三部分，处理流程为:首先，接收信号进行低噪放大并下变频到中频;然后，经压缩采样转换为压缩域数字信号;最后，直接对压缩域信号进行捕获、跟踪和解调处理，输出距离、速度和数据信息。

需要说明的是，图2所示系统中的压缩采样模块、压缩域信号捕获和压缩域伪码跟踪技术已经在其他文章中展开研究，本文主要研究对象是压缩域载波跟踪。在假设已经通过压缩采样模块获得压缩域数字直扩测控通信信号，且已成功完成压缩域信号捕获和伪码跟踪的情况下，对压缩域信号载波跟踪和解调方法进行研究。

3 压缩域Costas 环建模与分析

3.1 压缩域Costas 环路模型

直扩测控通信系统一般通过Costas 环来完成载波跟踪和数据解调等功能，它主要用来解调双边带抑制载波调制信号，是二相、四相相移键控信号的专用解调环路。在传统锁相环中，实质是通过计算输入信号和本地振荡器生成估计信号的加权内积来实现相位估计［3］。基于文献［6］提供的直扩测控通信信号稀疏性前提，根据文献［8］压缩域信号估计分析结论，并借鉴传统Costas 环工作原理，本文提出了一种针对压缩域信号的压缩域Costas 环路，其结构如图3所示。

压缩域Costas 环路可以实现压缩域直扩测控通信信号的载波跟踪和解调功能，主要包括压缩采样器(由Φ 表示)、鉴相器(由乘法器和低通滤波器构成)、环路滤波器和数控振荡器四部分。其中，数控振荡器用来产生同相、正交载波，并与再生伪码相关生成本地参考信号;压缩采样器实现对输入信号和本地参考信号进行压缩处理，输入信号与参考信号的同相信号及正交信号的压缩采样值分别相乘，两个乘法器输出经积分低通滤波器滤波后输出，并作为第三个乘法器的输入，乘法器输出结果经环路滤波后作为环路误差信号控制数控振荡器。另外，当环路锁定后，I 路输入压缩域信号经过压缩域解扩、解调后可以输出常规PCM 串行数据信号，送给位同步和帧同步等信息处理模块。

跟踪环路具有较高的实时性要求，这给压缩采样器提出了一些约束条件，包括因果性、低延迟和低复杂度等。随机解调压缩采样器满足上述约束条件，因此在本文研究过程中采用随机解调压缩采样器［9］。值得注意的是，在环路中需要给随机解调压缩采样器输入相同伪随机序列，保持积分器脉冲响应一致，并保证低速采样处理同步。

3.2 环路分析

在传统锁相环分析中，一般假设信号频率已经锁定，环路只需估计信号相位。类似地，假设压缩域环路的信号频率已锁定，仅需跟踪信号相位变化。首先给出输入信号数学模型［1］:

式中，P(·)是扩频伪码，D(·)是调制信息数据，w是输入信号频率，θ1是输入信号初始相位。则其对应的压缩采样值为

式中，L 是压缩比，pm［·］表示第m 个随机解调压缩采样器的抽头系数。本地生成的同相参考信号与正交参考信号可分别表示为

式中，Pn［n］表示本地再生伪码。通过随机解调压缩采样器等效模型，可得本地参考信号对应的压缩测量值分别为

不失一般性，选取同相支路展开分析，首先给出输入信号通过同相支路鉴相乘法器输出为

假设伪码已经准确跟踪同步，即Pn［k］= P［k］，且压缩采样器抽头系数服从伯努利分布，有(pm［ ·］)2=1，式(7)可以化简为

式中，

类似地，可得到正交支路鉴相乘法器输出为

根据式(8)～(11)可以发现，同相支路与正交支路的鉴相乘法器输出类似，主要包含两项:第一项是输入信号和本地生成参考信号的传统Nyquist 采样值之间相关输出的累加处理;第二项是压缩采样引入的交叉噪声项，即式(9)与式(11)，已知pm［·］与其他乘积项不相关且具有随机性，因此该项具有噪声特性。

积分清零器的积分时间取一个伪码周期TPN=NPNts，其中NPN是一个伪码周期对应的传统高速采样点数。由于积分清零器工作在压缩采样后的低速率，所以其积分时间内的积累点数为MPN=NPN/L，则可得I 路积分清零结果为

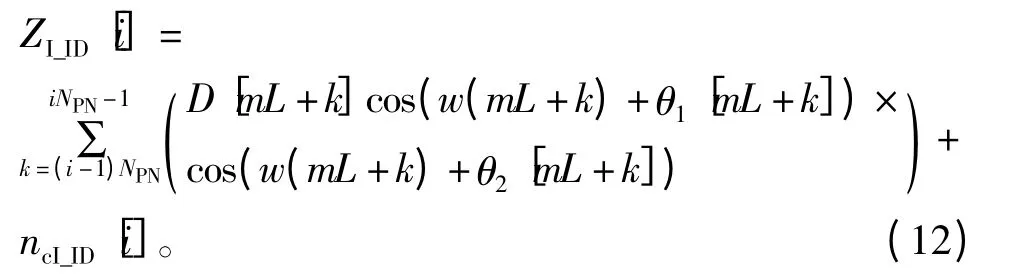
式中，

由式(12)可知，本文所提出环路的I 路积分清零结果与传统Costas 环路相似，区别在于多出了第二项，即式(13)，这是由压缩采样引入的交叉噪声项。同理，可得Q 路积分清零结果为

式中，

3.3 鉴相特性分析

锁相环路鉴相器常见的有二象限反正切鉴相器、点积功率鉴相器等多种类型，其中点积功率鉴相器的运算量中等，在低信噪比时性能较好［10］，本文主要采用采样点积功率鉴相器，则压缩域Costas 环路的鉴相器输出可表示为

把式(12)、式(14)代入式(16)，则有

式中，

根据式(17)可知，本文所提出环路的点积功率鉴相器输出与传统Costas 环采用点积功率鉴相器的情况相似，只是多出了第二项，这是由压缩采样引入的交叉噪声项所产生。

4 环路跟踪精度分析

4.1 交叉噪声特性分析

根据上一节分析结论可知，相对于传统载波跟踪环，本文所提出环路的压缩采样处理额外引入了一个交叉噪声项。不失一般性，选取同相支路对交叉噪声特性展开分析。根据该交叉噪声项式(9)，可以得到其均值表达式为

假设压缩采样器的伪随机抽头系数pm［·］的均值为零，方差为σpm，信号扩频调制解调的伪随机码P［·］的均值为零，方差为σP，两者相互独立，互相关为零，有

代入式(19)可得

根据方差定义，可得交叉噪声的方差为

把式(9)、式(21)代入式(22)，则有

已知pm［·］、P［·］和D［·］三者相互独立，互相关为零，并且(pm［·］)2= (P［ ·］)2=(D［ ·］)2=1，则式(23)可以化简为

类似地，可以得到正交支路引入交叉噪声的均值和方差分别为

由式(21)、式(24)～(26)可知，同相支路和正交支路引入的交叉噪声项都是零均值的白噪声，噪声方差相同，并与压缩比成正比。值得注意的是，当压缩比为1 时，即L=1，交叉噪声方差变为零，此时本文所提出的压缩域环路退化成传统锁相环路。

综上分析可知，相对于传统锁相环，压缩域Costas 环路虽然可以降低采样率或数据率，但是同时会在环路中添加额外的零均值白噪声，相当于给输入信号信噪比引入一个等效恶化量。假设输入信号载噪比为C/N0，输入噪声功率谱密度σ20 =N0Bn/2，已知输入噪声与引入交叉噪声不相关，两者互相关为零，则等效总噪声方差可表示为σ2all=σ20+σ2ncI，相应的等效输入载噪比为

式中，Bn是双边带前端带宽。

4.2 环路跟踪精度分析

载波跟踪环的跟踪精度决定速度测量精度，影响环路跟踪精度的因素主要包括环路热噪声和振荡器噪声［1］。由于环路中的大多数相位抖动源都是瞬时的，或是可以忽略的，传统环路跟踪误差源主要考虑热噪声，而本文提出环路又额外引入了交叉噪声项。文献［1］给出了传统载波跟踪环鉴相误差公式，考虑交叉噪声对输入信号载噪比影响，可得压缩域锁相环的跟踪误差表达式为

式中，BL是载波环路噪声带宽;Tf是频率积分时间，TID是积分清零时间间隔即相干积分时间;C/ (2σ2all/Bn)是等效输入信号载噪比;Bn是双边带前端带宽。把式(24)和式(27)代入式(28)，跟踪误差表达式可具体表示为

式中，L 是压缩比。根据式(29)，可以得到压缩域载波跟踪环跟踪误差的变化规律如下:

(1)频率跟踪误差σfCS与环路噪声带宽BL成正比，缩小BL可以降低环路跟踪误差;

(2)频率跟踪误差σfCS与相干积分时间TID和频率积分时间Tf都成反比关系，增大它们都可以降低跟踪误差，并且增大Tf的效果要比TID明显，同时TID的增大受到数据位跳变制约;

(3)频率跟踪误差σfCS与压缩比L 成正比，减小L 也可以降低跟踪误差，但同时会增大压缩采样的采样频率，因此为了获得一定跟踪精度，压缩比取值不能过大。

5 仿真实验及结果分析

对本文提出的压缩域Costas 环进行实验验证，主要思路是把其应用到直扩测控通信信号的载波同步跟踪，并与传统载波跟踪环路进行对比分析，分为可行性验证和性能分析两个阶段。

注意，仿真实验中信号参数主要参照现役主流直扩测控通信系统来设置，这样有利于与实际系统性能指标进行比对，但本文所提出压缩域环路主要受限于信号信息量，而不是信号带宽，实际上带宽越宽压缩域Costas 环路优势越明显。

5.1 可行性验证

可行性验证主要是验证压缩域Costas 环可行性。首先利用压缩采样器对信号进行压缩处理，获得压缩域信号，假设伪码已经同步，然后利用本文提出的环路技术对压缩域信号进行载波跟踪、同步解调处理，探讨多普勒信息提取精度和数据解调情况，并与传统环路进行对比分析。

信号参数设置:数据率为10 kb/s，伪码周期1023，码速率为10.23 Mchip/s，载波中心为70 MHz，原采样率为56 MHz，载噪比为56 dBHz，多普勒频率分为100 Hz阶跃和10 kHz/s斜升两种情况。

环路参数设置:阻尼系数0. 707，环路带宽500 Hz，相干积分时长0.1 ms，测速积分平滑时长5 ms，采用随机解调压缩采样器［8］，压缩比10。

压缩域Costas 环路的跟踪结果如图4所示。

图4 压缩域Costas 环跟踪结果Fig.4 Tracking results by compressed domain Costas loop

由图4可知，压缩域Costas 环路能够锁定频率阶跃和斜升两类输入信号，可以实现同步解调功能，输出常规PCM 串行数据，通过后续位同步和帧同步等处理可获得数据信息。根据统计可知，压缩域环路对两种信号的稳态跟踪误差分别为3.914 Hz、1.891 Hz，此频率跟踪精度基本能够满足一般测控通信系统测速要求，而且通过增加频率积分平滑时间还可以进一步提高跟踪精度。

5.2 性能分析

压缩域Costas 环路的性能分析主要从压缩比、载噪比和动态适应性三方面展开，针对频率阶跃和频率斜升两种信号，分别仿真分析环路跟踪精度随三个主要关注因素的变化规律。

5.2.1 压缩比对压缩域Costas 环路跟踪精度的影响

在实验1 中，载噪比56 dBHz，多普勒阶跃取500 Hz阶跃、斜升取100 kHz/s，环路带宽1500 Hz，频率积分平滑时长取50 ms，压缩比变化范围取［1，140］，其他参数与上一节相同，结果如5 所示。

图5 跟踪性能与压缩比关系图Fig.5 Relationship between tracking performance and compression ratio

由图5可知，针对两种类型信号，压缩域Costas环路的跟踪精度变化趋势保持一致，随着压缩比增大而减小，因此压缩域环路的跟踪精度会低于传统跟踪环路(即压缩取1 情况);当压缩比较小时，压缩采样引入的交叉噪声较小，环路跟踪误差缓慢增大，但只要压缩比不大于20，跟踪误差就可以保持在1 Hz以内，此频率跟踪精度能够满足一般测控通信系统的测速要求;当压缩比较大时，交叉噪声占据主导作用，环路跟踪误差会急剧增大，表明环路已经失锁。

5.2.2 载噪比对压缩域Costas 环路跟踪精度的影响

在实验2 中，压缩比取10，载噪比变化范围取［43，73］dBHz，信号动态参数设置与实验1 保持一致，其他参数与上一节相同，结果如6 所示。

图6 跟踪性能与信噪比关系图Fig.6 Relationship between tracking performance and SNR

由图6可知，压缩域环路跟踪精度在两种信号情况下的变化规律相同，随着载噪比降低而减小;当载噪比较高时，环路跟踪误差随信噪比降低而缓慢增大，但只要载噪比不低于54 dBHz，环路误差就可以保持在1 Hz以内，能够满足一般测控通信系统测速要求;当信噪比较低时，由于压缩采样引入交叉噪声和信号噪声的共同作用，会导致环路失锁，频率跟踪误差急剧增大。

5.2.3 压缩域Costas 环路的动态适应性

在实验3 中，载噪比56 dBHz，压缩比10，多普勒阶跃取［100，1000］Hz、斜升取［10，200］kHz/s，其他参数与上一节相同，结果如7 所示。

图7 跟踪性能与信号动态关系图Fig.7 Relationship between tracking performance and signal dynamic

由图7可知，针对频率阶跃和斜升两种类型信号，压缩域Costas 环路的跟踪精度在给出的动态范围内基本保持不变，说明压缩域环路的动态适应性较强;在1000 Hz频率阶跃或200 kHz/s频率斜升的高信号动态下，环路的跟踪误差能够分别保持在0.8 Hz、0.5 Hz以内，能够满足高动态环境下的测控通信系统测速要求。

5.3 仿真实验总结

通过以上仿真实验，可得出以下结论:

(1)本文所提出压缩域Costas 环可以正常工作，能够锁定压缩域直扩测控通信信号，并成功跟踪信号频率相位变化，同时完成信号解调，输出常规PCM 串行数据;

(2)压缩域环路跟踪精度与压缩比成反比、与载噪比成正比，其跟踪精度要略低于传统跟踪环路。在一定压缩比和信噪比范围内，环路跟踪误差缓慢增大，但只要压缩比不超过20、载噪比高于54 dBHz，跟踪误差可以保持在1 Hz以内，能够满足一般测控通信系统的测速要求;

(3)压缩域Costas 环路的动态适应性较强，在载噪比为56 dBHz、压缩比为10 条件下，能够完成跟踪1000 Hz阶跃和200 kHz/s斜升高动态信号，且跟踪误差分别保持在0.8 Hz、0.5 Hz以内，能够满足高动态环境下测控通信系统测速要求。

6 结束语

压缩感知理论已经在测控通信相关领域有一些应用尝试，能够有效降低采样率和数据率，但同时其重构算法复杂度偏高，需要大量计算资源消耗。针对压缩域信号的频率同步问题，本文提出了一种改进的压缩域Costas 环路技术，不再需要进行信号重构，可以直接从压缩域直扩测控通信信号中提取频率和相位信息，在计算复杂度方面具有很强优势。理论分析和仿真结果表明，本文所提出环路能够在压缩域中实现高动态信号的高精度载波跟踪和解调处理，跟踪精度基本能够满足一般测控通信的测速要求。后续工作将进一步研究基于压缩感知的直扩测控通信信号接收处理有关问题。

［1］ 刘嘉兴. 飞行器测控与信息传输技术［M］. 北京:国防工业出版社，2011:13－24.LIU Jiaxing. Spacecraft TT＆C and information transmission technology［M］. Beijing:National Defense Industry Press，2011:13－24.(in Chinese)

［2］ 杨小牛，楼才义，徐建良. 软件无线电技术与应用［M］. 北京:北京理工大学出版社，2010:22－30.YANG Xiaoniu，LOU Caiyi，XU Jianliang. Software radio technology and application［M］. Beijing:Beijing Institute of Technology Press，2010:22－30.(in Chinese)

［3］ Donoho D L. Compressed sensing［J］，IEEE Transactions on Information Theory，2006，52(4):1289－1306.

［4］ Kazunori H，Masaaki N，Toshiyuki T.A user＇s guide to compressed sensing for communications systems ［J］. IEICE Transactions on Communications，2013，96(3):685－712.

［5］ Cheng Y H，Yang W G，Zhao J. Compressive sensing for DS TT＆C signals based on basic dictionary building［C］// Proceedings of 2014 the 27th Conference of Spacecraft TT＆C Technology in China.Guangdong:IEEE，2014:211－221.

［6］ Polo Y L，Wang Y，Leus G. Compressive wide－ band spectrum sensing［C］//Proceedings of 2009 International Conference on Acoustics，Speech and Signal Processing.Taipei，Taiwan:IEEE，2009:2337－2340.

［7］ Meng J，Ahmadi J，Li H S，et al. Sampling rate reduction for 60 GHz UWB communication using compressive sensing［C］//Proceedings of the 43rd Asilomar Conference on Signals，Systems and Computers. Pacific Grove，CA:IEEE，2009:1125－1129.

［8］ 程艳合，杨文革. 一种针对压缩域信号的新型锁相环技术［J］. 电讯技术，2015，55(3):256－261.CHENG Yanhe，YANG Wenge. A new phase locked loop technique for compressed domain signal［J］. Telecommunication Engineering，2015，55 (3):256－ 261.(in Chinese)

［9］ Smaili S，Massoud Y. Accurate and efficient modeling of random demodulation based compressive sensing systems with a general filter［C］// Proceedings of 2014 International Symposium on Circuits and Systems. Melbourne:IEEE，2014:2519－2522.

［10］ John G P，Masoud S.数字通信［M］.5 版.张力军，译.北京:电子工业出版社，2013:201－215.John G P，Masoud S. Digital communications ［M］. 5th ed. Translated by ZHANG Lijun.Beijing:Publishing House of Electronics Industry，2013:201－215.(in Chinese)