一种基于场强差的移动台定位改进算法*
2015-03-18毛永毅张晓佳
毛永毅,张晓佳
(西安邮电大学 电子工程学院,西安710061)
1 引 言
目前,国内外对无线定位的理论研究已经相当成熟,实践应用覆盖各个领域。但由于信号在传播过程中受到传播误差、多径效应、非视距误差等干扰的影响,测量信号与实际信号之间会有一定的偏差,从而使得移动台定位的准确率大大降低。因此,如何提高定位精度也越来越成为人们关注的焦点。常用的定位方法有到达时间(Time of Arrival,TOA)定位[1]、时间差(Time Difference of Arrival,TDOA)定位[2]、到达角度(Angle of Arrival,AOA)定位[3]、场强(Field Strength of Arrival,SOA)[4]定位、场强差(Field Strength Difference of Arrival,SDOA)定位[5]等。场强差定位方法由于无需添加其他物理设备,成本低,通过改进算法就可以得到较高的定位精度,因此得到了广泛应用。
小波变换[6-7]可以通过母小波函数对信号进行平移和尺度变化处理,从信号中提取有用信息,不仅处理速度快而且精度高,因此应用也越来越广泛。本文通过小波变换来修正信号的传播误差,再利用修正过的场强差值运用经典Chan[8]算法来进行移动台位置估计,最后用Matlab 对该算法进行仿真,并对仿真结果进行分析比较。
2 信道模型
实际生活中,信号在传播过程中会受到多种障碍物影响,使得实际接收到的信号与源信号有很大的误差,导致通过这些信号得到的定位结果精度很低。场强信号传播过程中受传播误差影响较大,一个好的传播模型可以很大程度上抑制传播误差,因此需对不同的传播环境匹配不同的传播模型,并加以不同的修正因子来进一步减小误差。常用的模型有Okumura Hata 模型[9]、Okumura 模型、COST-231Hata 模型[10]、WIM 模型、Egli 模型、Walfish 模型等。Okumura 模型在预测城区信号时应用最为广泛,适用频率为150~1920 MHz,距离为1~100 km,天线高度为30~1000 m。
Okumura Hata 模型是对Okumura 模型的改进。该模型是根据实际测量数据建立的模型,能提供比较全的数据,在实际移动台定位中得到了广泛应用。
该模型公式为

式中,fc是载波中心频率(MHz);hm是移动台天线的有效高度(m);hb是基站天线的有效高度(m);d 是移动台与基站之间的距离(km);a(hm)是移动台天线的高度修正因子,在不同的传播环境下有不同的取值,不同情况近似值如下:
中小城市修正:

大城市修正:
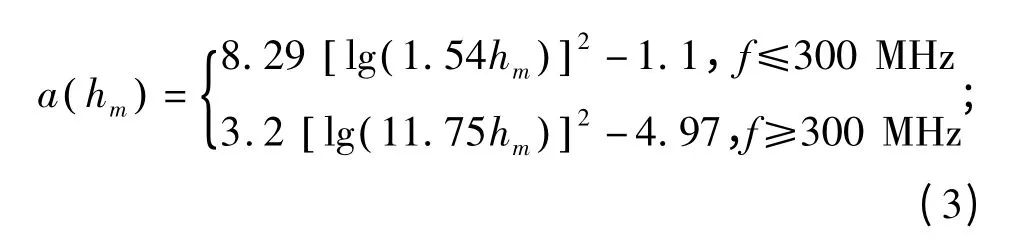
郊区:

3 场强差值定位算法
图1为本文定位算法模型,该方案既不需要增加额外的硬件设备也无需时间同步。图中BS0 为服务基站,MS 为被定位移动台。

图1 场强差定位模型Fig.1 The field strength difference positioning model
在本文提出的基于场强差的定位改进算法中,假设由服务基站测量得到的附近各基站场强强度为EBS={EBS1,EBS2,…,EBSn},其中EBSn是服务基站上报的第n 个基站的场强强度,由移动台测量得到的附近各服务基站的场强强度为EMS={EMS1,EMS2,…,EMSn},其中EMSn是移动台测得的第n 个基站的场强强度,而各邻近基站的实际发射场强强度为E={E1,E2,…,E3},En为第n 个基站的场强发射强度。将服务基站所上报的场强强度衰减系数表示为

那么,由移动台所上报的场强衰减系数表示为

由上述两式可以得到

根据上文中的Okumura Hata 传播损耗模型有
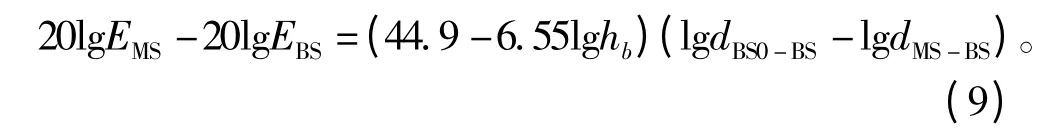
式中,dMS-BS和dBS0-BS分别表示移动台到各基站的距离和服务基站到各基站的距离,其中服务基站与各基站的距离为已知,根据公式(9)可以得到dMS-BS的估计值,然后再利用Chan 算法进行移动台位置估计。
4 算法描述
4.1 小波变换原理
小波变换理论是当今信号处理领域和数学领域中发展迅猛的新领域,其应用相当广泛。小波变换其实就是用一些特殊的函数作为基,然后将得到的信号数据变换为级数系列从而发现其频谱特性并用来实现其相应的数据处理。通过将不需要的频带上的小波系数置零处理或是赋予足够小的权重,从而有效地抑制噪声。
设Ф(t)满足下列条件:
(1)Ф(t)是一平方可积函数,即Ф(t)∈L2(R);
上面两个条件为小波变换的可容性条件,Ф(t)经过傅里叶变换得到Ψ(ω),Ф(t)被称为小波母函数或小波函数。
设小波消噪的原理模型为

式中,s(X)是实际得到的含有噪声的信号;e(X)是此刻的噪声信号,一般处在信号的高频部分;f(X)是去除噪后的信号,一般处在信号的低频部分。
对s(X)进行小波分解,如图2所示,最终得到的ca3 为近乎平稳的信号,分布在信号的低频段;cd1、d2、cd3 则是噪声主要成分,处在信号的高频段。所以如果要滤除噪声就要选择合适的门限值对其系数进行对应的处理,然后通过小波逆变换,重构出原始信号。

图2 小波变换的三层分解结构Fig.2 The three layers decomposition structure of wavelet transform
对时变信号f(t)∈L2(R)进行正交小波分解[11]得到

式中,N 为小波分解的层数,dj,k为小波分解系数,cj,k为小波尺度分解系数。
4.2 小波消噪步骤
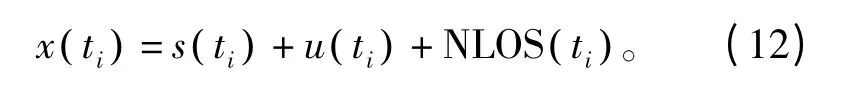
设x(ti)为在ti时刻的场强测量值,则有式中,s(ti)是ti时刻的真实测量值;u(ti)是ti时刻的传播误差,是零均值且服从高斯分布的随机序列。
(1)由各个基站得到的输入向量为:S =[SDOA1,SDOA2,SDOA3,SDOA4,SDOA5,SDOA6,SDOA7],先确定分解层数,选择合适的小波对上述场强差信号进行小波变换,由此得到其小波系数;
(2)利用如下经验公式[12]来计算不同尺度下的均方误差:

(3)由上述步骤得到的均方误差,使用如下计算方法算出不同尺度系数的阈值,从而求出新的小波系数:

(4)对上述阈值处理后的小波系数进行逆小波变换,把各层小波高频系数和低频系数进行信号重构,即可估计出原始信号。
4.3 基于小波分析的Chan 定位算法
由于信号在传播过程中受传播误差影响较大,对场强差定位精度影响较大,利用小波变换来修正场强测量数据,进一步减小测量值中的传播误差,再通过经典Chan 算法进行位置估计,定位精度将会得到有效提高。具体的定位步骤如下:
(1)先由测量得到K 组带有传播误差的场强差数据,确定合适的小波函数和分解层数,通过小波变换对其进行正交小波分解得到对应的小波系数;
(2)用上述方法计算阈值,对得到的新的小波系数进行逆变换,重构出滤除噪声的场强差信号值;
(3)利用修正后的数据运用经典Chan 算法进行移动台位置估计。
5 定位算法性能仿真与分析
在衡量定位算法的性能时,一般需要一个统一有效的性能指标来对定位算法的结果进行公平公正的评价。本文采用均方根误差(RMSE)法,其他常用的还有几何精度因子法、克拉美-罗下界和圆误差概率衡量误差等。
RMSE 方法计算简单,定位准确率相对较高,该值越小证明定位算法的精确度越高,该值稳定说明算法具有稳定性,因此本文采用均方根误差作为算法的性能指标。
设MS 的坐标为(x,y),(x',y')为MS 的估计坐标,则均方根误差RMSE 可表示为

对本文提出的基于小波变换的场强差定位改进算法进行Matlab 跟踪仿真以验证该算法的可靠性。本次仿真采用Daubechies 小波对信号进行三层分解,小区半径选取常用宏蜂窝小区半径1000~3000 m,并与未采用小波变换优化的Chan 算法进行对比。
图3为当小区半径不同时,本文基于小波变换的场强差定位改进算法与经典Chan 算法定位结果对比图。由图可知,本文改进算法的性能明显优于直接采用Chan 算法定位。随着小区半径的扩大,传播误差会随着传播距离的增加而不断增加,而小波变换可以很好地抑制这种误差,所以该算法在小区半径增加时仍然能够保持平稳的定位性能。
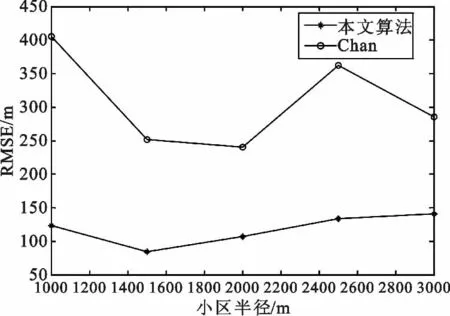
图3 不同小区半径下定位算法比较Fig.3 RMSE of the positioning algorithm under different cell radius
图4为测量误差不同时,本文所采用的定位方法与直接采用Chan 算法定位结果对比图。由仿真结果可以看出,随着测量误差的不断增大,定位性能也会逐渐下降,但是相对于直接采用Chan 算法定位,本文的移动台定位改进算法均方根误差增长缓慢,效果更加稳定,说明小波变换可以很好地消除传播误差对信号的影响。

图4 不同测量误差下定位算法比较Fig.4 RMSE of the positioning algorithm under different measurement error
6 结束语
本文提出了一种基于场强差的移动台定位改进算法,针对不同的传播环境有不同的传播因子,使得定位结果更加精确,从而减小了传播误差以及系统测量误差对定位精度的影响;然后结合小波变换来修正测量数据,进一步减小误差;最后利用Chan 算法进行位置估计。从实验的模拟仿真可以看出,本文提出的算法相对于直接采用经典Chan 算法定位精度更高,性能更稳定,有良好的可行性,但是在测量误差为0.4 μs时,会出现较大奇异误差,本文尚难以解释,这也是下一步研究的课题。
[1] 何燕,胡捍英,周山.对抗NLOS 误差的TOA/AOA 混合无线定位算法[J].电讯技术,2006,46(6):167-171.HE Yan,HU Hanying,ZHOU Shan. The TOA/AOA hybrid location algorithm against the NLOS error[J]. Telecommunication Engineering,2006,46(6):167- 171.(in Chinese)
[2] 朱朝晖. 时差定位原理及其应用[J]. 无线电工程,2006,36(8):52-64.ZHU Chaohui. The principle and application of TDOA location[J]. Radio Engineering of China,2006,36(8):52-64. (in Chinese)
[3] 王洪雁,兰云飞,裴炳南,等. 非视距环境下基于到达时间差的一种定位算法[J]. 计算机仿真,2007,24(9):116-119.WANG Hongyan,LAN Yunfei,PEI Bingnan,et al. A location algorithm based on TDOA under NLOS environment[J]. Computer Simulation,2007,24(9):116- 119.(in Chinese)
[4] 王建军,邓平,李金伦.一种基于场强差的GSM 网络移动台定位方法[J].信息技术,2006(1):24-26.WANG Jianjun,DENG Ping,LI Jinlun. A mobile location method based on field strength difference of GSM network[J]. Information Technology,2006 (1):24- 26.(in Chinese)
[5] Wang X,He Z S. Target motion analysis in three-sensor TDOA location system[J]. Information Technology Journal,2011,10(6):1150-1160.
[6] 成昊,吕明,唐斌,等. 一种基于小波分解的直扩信号检测方法[J].电讯技术,2006,46(6):67-70.CHENG Hao,LUY Ming,TANG Bin,et al. A DSSS signal detection based on the wavelet decomposition[J].Telecommunication Engineering,2006,46(6):67-70.(in Chinese)
[7] 张仁辉,杜民.小波分析在去噪中的应用[J].计算机仿真,2005,22(8):69-72.ZHANG Renhui,DU Min. Wavelet analysis application in denoising[J]. Computer simulation,2005,22(8):69-72. (in Chinese)
[8] 范平志,邓平,刘林.蜂窝无线定位[M].北京:电子工业出版社,2002.FAN Pingzhi,DENG Ping,LIU Lin. Cellular wireless location[M]. Beijing:Publishing House of Electronics Industry,2002. (in Chinese)
[9] 聂颖,易强,江红,等.CDMA 无线定位系统的基站选择算法[J].电讯技术,2004,44(1):30-34.NIE Ying,YI Qiang,JIANG Hong,et al. The base station selection algorithm of CDMA wireless positioning system[J]. Telecommunication Engineering,2004,44(1):30-34. (in Chinese)
[10] 付昆鹏.无线通信中电波传播模型的研究[D].广州:华南师范大学,2009.FU Kunpeng. Research on radio wave propagation model in wireless communication[D]. Guangzhou:South China Normal University,2009. (in Chinese)
[11] 卓宁. 小波分析技术在GPS 数据预处理中的应用[J].中国惯性技术学报,2009,17(2):184-186.ZHUO Ning. Application of wavelet analysis in GPS data processing[J]. Journal of China Inertial Technology,2009,17(2):184-186. (in Chinese)
[12] Mao J D. Noise reduction for lidar returns using local threshold wavelet analysis[J].Optical and Quant- um Electronics,2012,43(1-5):59-68.
