求半正定Hermitian 矩阵特征向量的改进乘幂法*

张 雷

(中国西南电子技术研究所，成都610036)

1 引 言

在无线通信多天线系统中，基于信道矩阵奇异值分解/特征值分解的预编码/波束成形技术［1－2］主要问题是计算半正定Hermitian 矩阵的最大前n 个特征值对应的特征向量(为方便，将这些特征向量分别称为第i(i=1，2，…，n)特征向量)。矩阵特征值分解主要有两大类方法:一类是矩阵变换方法，如Jacobi 方 法［3］;另 一 类 是 向 量 迭 代 法，如 乘 幂法［4－5］、子空间迭代法［6］。Jacobi 方法通常得到矩阵的全部特征值及其对应特征向量，而乘幂法是求解半正定Hermitian 矩阵最大特征值对应特征向量的一种经典方法。文献［5，8］进一步指出将乘幂法与压缩法相结合可逐个求出半正定Hermitian 矩阵的所有特征向量。

但是，上述经典乘幂法(及其与压缩法的结合)存在两个主要问题:一是迭代次数固定，使得待分解矩阵的随机变化和初始向量的不同选择导致计算精度波动较大——较小迭代次数使得部分矩阵计算精度不高，较大迭代次数尽管能更好保证计算精度，但会显著增加计算复杂度;二是较大特征值对应特征向量的计算误差会传播至较小特征值对应特征向量的计算。

着眼于解决以上问题，在前述研究基础上，本文提出了计算第一特征向量的基于向量距离的改进乘幂法，在每次迭代时计算本次所得向量与前一次所得向量的距离，当该向量距离大于预先设定的阈值后即停止迭代;同时，还证明了所提方法的收敛性。此外，将改进乘幂法与压缩法相结合，给出了计算第二特征向量的算法，并证明了存在误差传播时该算法的收敛性。理论计算结果表明，对4 阶半正定Hermitian 随机矩阵，在相同计算精度前提条件下，相比经典乘幂法(及其与压缩法的结合)，所提方法可至少降低一半计算复杂度。

符号说明:大小写黑斜体字母分别表示矩阵和(列)向量;(·)T和(·)H分别表示矩阵的转置和Hermitian 转置;‖·‖表示矩阵的Frobenius 范数。

2 第一特征向量的计算

2.1 经典乘幂法简介

对一m 阶半正定Hermitian 矩阵R，设其m 个特征值按降序排列为λ1≥λ2≥…≥λm≥0，对应的特征向量分别为u1，u2，…，um。经典乘幂法由算法1 给出［4］。

算法1:经典乘幂法计算第一特征向量

Step 1:初始化m 维单位向量x(0);

Step 2:设k=1，2，…，K1，计算

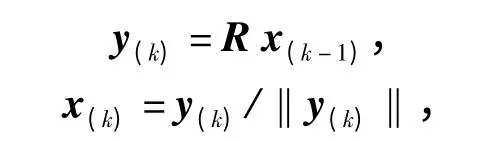
则x(k)为所求第一特征向量u1。

考察算法1 的收敛性。因u1，u2，…，um构成m维向量空间的一组正交基，x(0)可表示为

因篇幅所限，仅研究λ1为单特征值(对应的特征向量有且仅有一个)的情形。为讨论方便，设

显然有1 =r1＞r2≥…≥rm≥0 成立。定义x(k)和u1的距离为

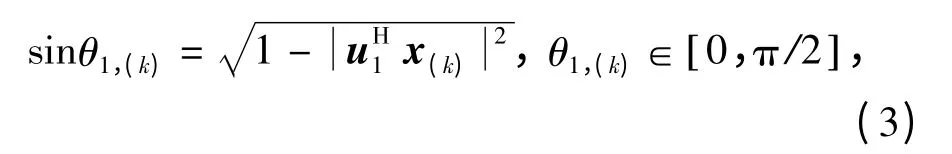
它反映了x(k)与u1之间的差异程度，sinθ1，(k)越小，x(k)与u1越接近。一般地，有如下定理［4］:

定理1 若a1≠0，则对由算法1 求得的x(k)，下式成立(UB 表示上界，下同):

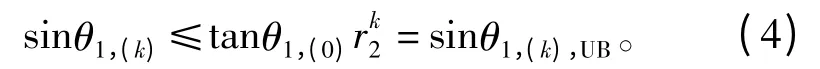
由定理1，只要a1≠0，tanθ1，(0)就为一有限正数，因此，当k→"时，有sinθ1，(k)，UB→0，即x(k)→ejφu1(φ 为任一实数)，这表明x(k)将随着k 的增大而收敛于u1。

2.2 基于向量距离的乘幂法

虽然定理1 保证了算法1 的收敛性，但给定x(0)和K1，不同R 得到的计算误差sinθ1，(k)差异较大，主要原因是:x(0)与u1之间距离不同使得|a1|取值不同;R 特征值分布不同使得ri取值不同。为此，可考虑引入一个合适的“收敛条件”，只要满足该条件，即停止迭代，并保证对不同R 得到的计算误差sinθ1，(k)均不超过某一阈值。由此，将算法1 改进得算法2。

算法2:基于向量距离的乘幂法计算第一特征向量

Step 1:初始化m 维单位向量x(0)、d =1、k =1、ε1(ε1＜1);

Step 2:计算

直到d ＜ε1为止，则x(k)为所求第一特征向量u1。

由定理1 知，只要算法2 中的d 逐渐减小并收敛于某一定值，就能有效控制迭代次数，并使求出的x(k)逐渐收敛于u1。下面分析d 的收敛性。定义x(k)和x(k－1)之间的距离为

一般地，有如下定理:

定理2 对由算法2 求得的x(k)和x(k－1)，若a1≠0，则下式成立:

证明:根据算法2，有

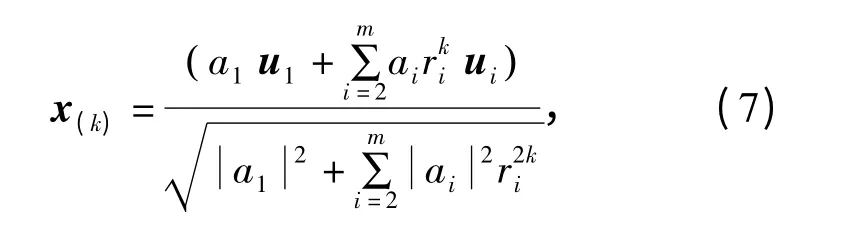
从而

因此，定理2 得证。

由定理2，只要a1≠0，当k→"时，有sinφ1，(k)，UB→0，即x(k)→ejφx(k－1)(φ 为任一实数)，从而保证了算法2 的收敛性。

3 第二特征向量的计算

3.1 乘幂法与压缩法的结合

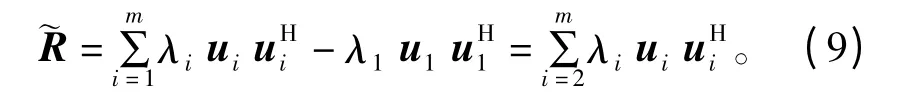
由此可见，R 的第二大特征值λ2和第二特征向量u2恰好分别是的第一大特征值和第一特征向量。因此，这种乘幂法与压缩法的结合可将“计算R的第二特征向量”问题转化为“计算的第一特征向量”问题，从而再次运用算法1 或算法2 求解。与第2 节类似，本文仅研究λ2为单特征值的情形。此外，考虑到误差传播的影响(详见3.2 节)，在计算u1时拟采用算法2，以便对任意矩阵R 都能将计算u1的误差控制在较小水平。

算法3:基于向量距离的乘幂法计算第二特征向量

Step 1:同算法2;

Step 3:初始化m 维单位向量z(0)、d =1、k =1、ε2ε2()＜1 ;

Step 4:计算

直到d ＜ε2为止，则z(k)为所求第二特征向量u2。

3.2 误差传播的影响

理论上，乘幂法与压缩法的结合可依次计算出R 的所有特征向量，但实际上总存在误差，此误差传播会降低后续特征向量的计算精度。本小节分析珘u1≠u1对计算u2带来的影响。为简化推导，假设珘u1仅含u1和u2两个分量(只要ε1值较小，这个假设几乎总是成立)，即

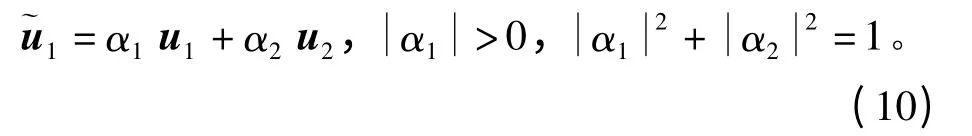
与前文类似，定义z(k)和u2的距离为

设初始向量

一般地，有如下定理:

定理3 对由算法3 求得的z(k)(k≥1)，若b1α2≠b2α1，则下式成立(LB 表示下界)

式中，

证明:根据算法3，有

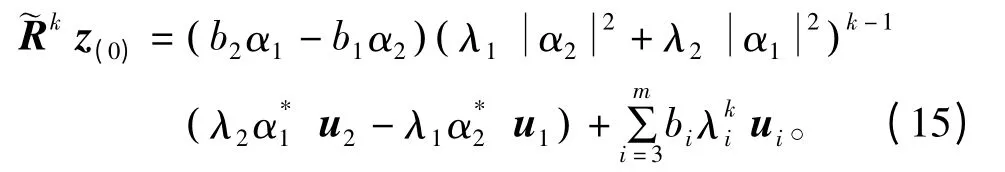
若b1α2=b2α1，则式(15)退化为

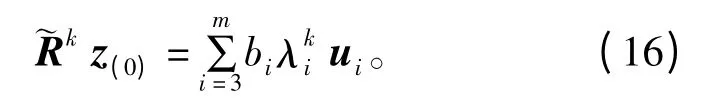
这表明z(k)中不包含u1和u2两个分量，有sinθ2，(k)=1。现考察b1α2≠b2α1情形，由式(15)得

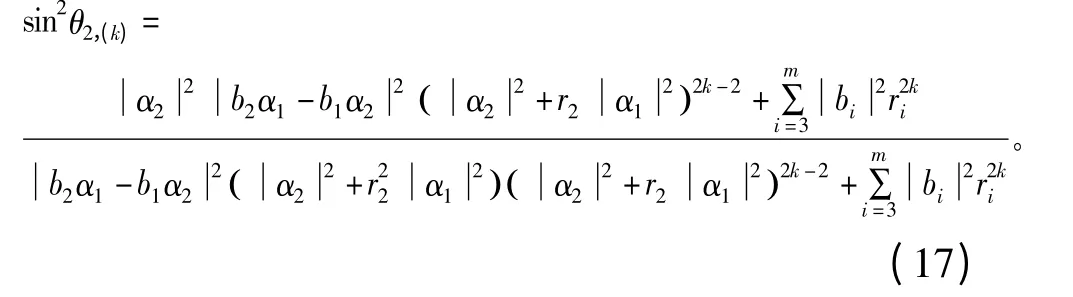
首先，有

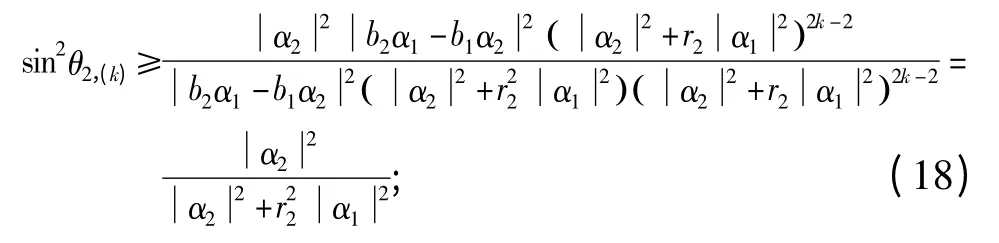
其次，有

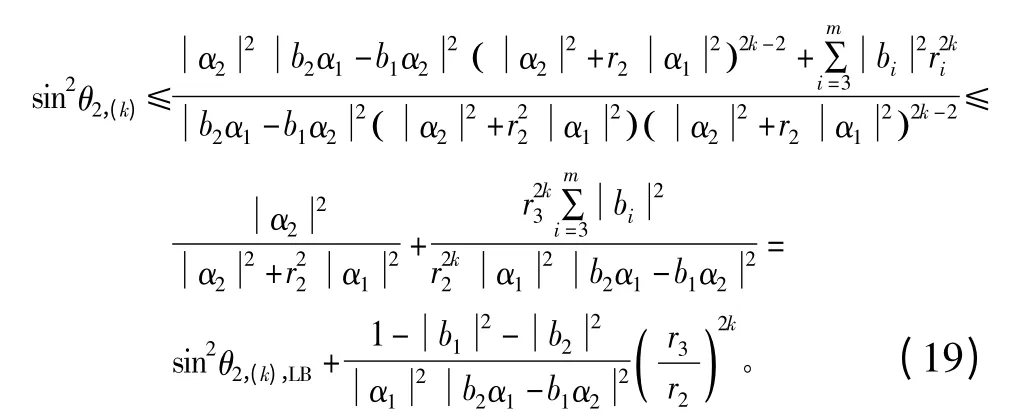
因此，定理3 得证。

从定理3 可看出:

(1)若λ3＜λ2(即λ2为单特征值)，则当k→"时，有sinθ2，(k)，UB→sinθ2，(k)→sinθ2，(k)，LB;

(2)因sinθ2，(k)，LB为与k 无关的定值，故当α2≠0 时，即使k→"，sinθ2，(k)也不会趋于0;这与2.2 节求解u1的结论不同。当然，若计算u1的精度足够高，使得sinθ2，(k)，LB足够小，则可使sinθ2，(k)收敛于足够小的值。

下面再考察算法3 步骤4 中d 的收敛性。定义z(k)和z(k－1)之间的距离为

一般地，有如下定理:

定理4 对由算法3 求得的z(k)和z(k－1)，下式成立:

式中，

证明:根据算法3，当k≥2 时，有

式中，p1、c1和c2由式(22)给出，且ci=bi，pi=ri(i=3，4，…，m)。进一步，有

由定理4，即使计算第一特征向量时存在误差，sinφ2，(k)，UB也将随着第二次迭代次数k 的增加而不断减小，并最终趋于0，从而保证了算法3 的收敛性。

4 计算复杂度分析

在算法3 中，将计算第一特征向量的Step1 和计算第二特征向量的Step 4(迭代次数为K2)都应用经典乘幂法的算法命名为算法4。设算法1 和算法2 计算第一特征向量的迭代次数分别为K1和L1，算法3和算法4 计算第二特征向量的迭代次数分别为L1(Step 1)和L2(Step 4)、K1(Step 1)和K2(Step 4)，算法1、算法2、算法3 和算法4 的复数乘法次数分别约为K1(m2+3m/4)、L1(m2+7m/4)、(L1+L2+2)m2+7 (L1+L2)m/4 和 (K1+K2+2)m2+3 (K1+K2)m/4，在5.2节中将结合随机矩阵计算结果进一步讨论。

5 计算结果

5.1 确定矩阵计算结果

本小节提供R 为确定矩阵时的计算实例，以验证定理1～定理4 的正确性。R 由式(25)给出:

其特征值从大到小依次为10、6、4、2。

实例1 用算法1 或算法2 计算第一特征向量，设x(0)= [ 1 0 0 0]T。图1给出了sinθ1，(k)、sinθ1，(k)，UB、sinφ1，(k)和sinφ1，(k)，UB与迭代次数k 之间的关系。可以看出，它们都随着k 的增大逐渐趋于0，且4 条曲线斜率几乎一致，这与定理1 和定理2结论相符。

图1 sinθ1，(k)、sinθ1，(k)，UB、sinφ1，(k)和sinφ1，(k)，UB与迭代次数k 之间的关系Fig.1 sinθ1，(k)，sinθ1，(k)，UB，sinφ1，(k)and sinφ1，(k)，UB vs. iteration number k

实例2 用算法3 计算第二特征向量，设x(0)=z(0)= [ 1 0 0 0]T。图2给出了阈值ε1取0.1和0. 001 时sinθ2，(k)、sinθ2，(k)，LB和sinθ2，(k)，UB与Step 4迭代次数k 之间的关系。可以看出:对同一ε1，sinθ2，(k)和sinθ2，(k)，UB都随着k 的增加而收敛于sinθ2，(k)，LB;对不同的ε1，sinθ2，(k)，LB随着ε1的减小而降低，且 大 致 与 ε1的 数 量 级 相 当，sinθ2，(k)和sinθ2，(k)，UB收敛于sinθ2，(k)，LB所需迭代次数也逐渐增加，这与定理3 的结论相符。

图2 sinθ2，(k)、sinθ2，(k)，LB和sinθ2，(k)，UB与算法3 中Step 4 迭代次数k 之间的关系Fig.2 sinθ2，(k)、sinθ2，(k)，LB and sinθ2，(k)，UB vs. iteration number k of Step 4 in Algorithm 3

图3给出了阈值ε1取0.1 和0.001 时sinφ2，(k)和sinφ2，(k)，UB与步骤S4 迭代次数k 之间的关系。可以 看 出，在 两 种 ε1取 值 情 况 下，sinφ2，(k)和sinφ2，(k)，UB都随着k 的增加而逐渐减小，且斜率几乎相同，这与定理4 的结论相符。

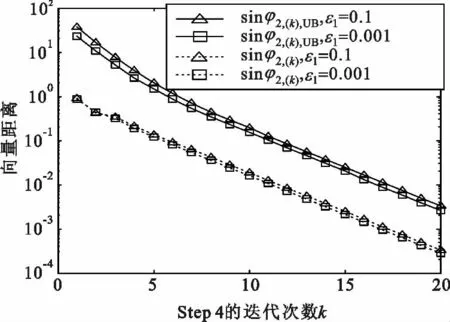
图3 sinφ2，(k)和sinφ2，(k)，UB与算法3 中Step 4 迭代次数k 之间的关系Fig.3 sinφ2，(k)and sinφ2，(k)，UB vs. iteration number k of Step 4 in Algorithm 3

5.2 随机矩阵计算结果

本小节利用Matlab 随机产生半正定Hermitian矩阵，以更好地比较经典乘幂法和所提改进乘幂法。具体方法为:设m=4，先用

生成4 阶随机矩阵A，再用R=AHA 产生R;一共独立产生10 000次R。事实上，当应用于无线通信多天线系统时，A 可视为收发两端之间的信道衰落随机矩阵，R 的特征向量即为相应的预编码/波束成形向量。此外，真实的第一特征向量和第二特征向量由Matlab 函数eig 求得。

首先考察第一特征向量的计算。图4对比了算法1 和算法2 计算出的第一特征向量与真实值距离(用sinθ1表示，由式(3)计算)的累积分布函数。对算法1，由于迭代次数固定，sinθ1波动范围很大，不易控制计算精度。K1= 5 和K1= 10 对应的P(sinθ1≥0.1)值分别约为0.18和0.04;当K1=20时，才有P(sinθ1≥0.1)≈0。对算法2，ε1=0.01和ε1= 0.001 分别对应于P(sinθ1≥0.1)≈0 和P(sinθ1≥0.01)≈0，对应的迭代次数均值 珔L1分别为7.3和10.9。为比较公平，将P(sinθ1≥0.1)≈0 作为计算精度要求，由第4 节分析知，算法1 和算法2的复数乘法次数分别约为380 和168。这表明，相对于算法1，算法2 不仅能将几乎所有矩阵的计算精度控制在较高水平，还降低了约56%的计算复杂度。

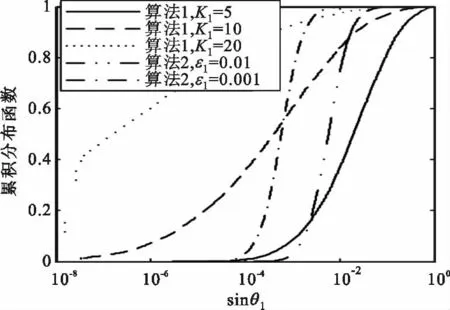
图4 sinθ1 的累积分布函数Fig.4 The cumulative distribution function of sinθ1

接着考察计算第二特征向量的结果。图5给出了算法3 和算法4 求出的第二特征向量与真实值距离(用sinθ2表示，由式(11)计算)的累积分布函数，其特点与图4类似。对算法4，sinθ2波动范围很大;K1=K2=5 和K1=K2=10 对应的P(sinθ2≥0.1)值分别升至约0.4 和0.06，当K1= K2=20 时，才有P(sinθ2≥0.1)≈0。对算法3，ε1=ε2=0.01 和ε1=ε2=0. 001 分别对应于P(sinθ2≥0. 1)≈0 和P(sinθ2≥0.01)≈0，对应的Step 4 的迭代次数均值珔L2分别为6.1 和8.8。同样将P(sinθ1≥0.1)≈0 作为计算精度要求，算法3 和算法4 的复数乘法次数分别约为340 和792，即算法3 比算法4 降低了约57%的计算复杂度。

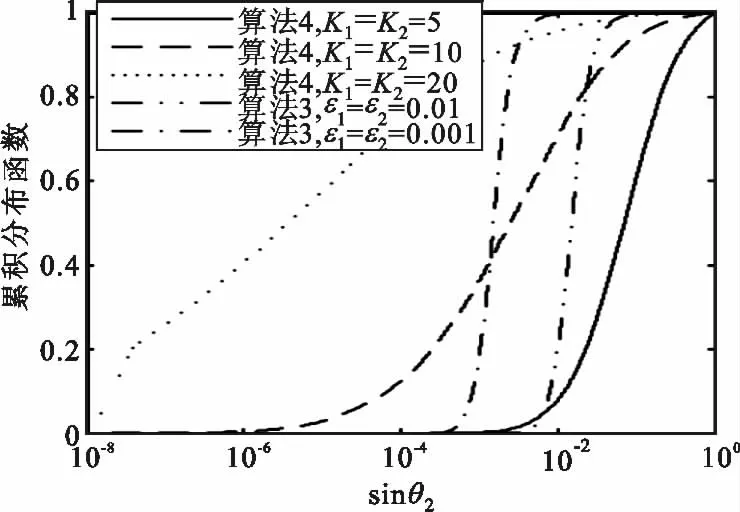
图5 sinθ2 的累积分布函数Fig.5 The cumulative distribution function of sinθ2

6 结束语

计算半正定Hermitian 矩阵最大前n 个特征值对应特征向量是工程中的常见问题，在无线通信多天线系统的预编码/波束成形技术中已有诸多应用。相比经典乘幂法(及其与压缩法的结合)，本文所提基于向量距离的改进乘幂法(及其与压缩法的结合)能在保证计算精度的前提下显著降低计算复杂度，更有利于工程实现。尽管本文仅研究了计算第一特征向量和第二特征向量情形，但进一步通过3.1节所述的逐层压缩，所提方法及理论分析框架也可推广至计算所有特征向量情形。

此外，为讨论方便，在计算第i(i =1，2)特征向量时，本文均假设第i 特征值为单特征值。文献［4，8］指出，第i 大特征值为多重特征值的情形并不影响乘幂法及其与压缩法的结合。因此，本文所提方法也适用于存在多重特征值的情形。

［1］ 3GPP TS 36.211(V9.1.0)，Evolved Universal Terrestrial Radio Access (E－UTRA);Physical Channels and Modulation (Release 9)［S］.

［2］ 郭建光，王宇欣，孙占委. TD－LTE TM8 传输模式分析［J］. 移动通信，2014，38(12):33－36.GUO Jianguang，WANG Yuxin，SUN Zhanwei. Research on TD－LTE TM8 Transmission Mode［J］. Mobile Communications，2014，38(12):33－36. (in Chinese)

［3］ Sleupen G，Vander A. A Jacobi－Davidson Iteration Method for Linear Eigenvalue Problem［J］. SIAM Journal on Matrix Analysis and Applications，1996，17(2):401－425.

［4］ Golub G H，Van Loan C F. Matrix Computation［M］.3版.北京:人民邮电出版社，2009.Golub G H，Van Loan C F.Matrix Computation［M］. 3rd ed.Beijing:People's Posts＆Telecom Press，2009.(in English)

［5］ 张贤达. 矩阵分析与应用［M］. 北京:清华大学出版社，2004.ZHANG Xianda. Matrix Analysis and Applications［M］.Beijing:Tsinghua University Press，2004. (in Chinese)

［6］ Bramble J H，Knyazev A V，Pasciak J E. A Subspace Preconditioning Algorithm for Eigenvalue Computation［J］. Advances in Computational Mathematics，1996(6):159－189.

［7］ Paulraj A，Nabar R，Gore D. Introduction to space－time wireless communications (photocopy)［M］. 北京:清华大学出版社，2005.Paulraj A，Nabar R，Gore D.Introduction to space－time wireless communications (photocopy)［M］. Beijing:Tsinghua University Press，2005.(in English)

［8］ 张青，苟国楷，吕崇德. 乘幂法的改进算法［J］. 应用数学与计算数学学报，1997，11(1):51－55.ZHANG Qing，GOU Guokai，LYU Chongde. An Improvement Scheme for the Power Method［J］. Communication on Applied Mathematics and Computation，1997，11(1):51－55. (in Chinese)