m子序列的特性研究

张爱雪，年夫生，韩春

(安徽工程大学电气工程学院安徽省电气传动与控制重点实验室，安徽芜湖241000)

基于线性移位寄存器(LFSR)构造产生的伪随机m序列是成熟的理论，m序列具有周期性、游程性、平衡性和相关性良好的伪随机性。但m序列的数目有限，线性复杂度低，非线性度为零，往往不能满足实际应用的需要。近年来，研究出更具有科学和社会价值的伪随机m序列是国内外相关领域的热点问题。本文主要讨论基于m序列构造出的第一类m子序列的线性复杂度和非线性度，从而证明第一类m子序列具有很好的线性复杂度和良好的非线性度。

1 m序列和m子序列

1.1 m序列及其特性

假设以F2上n次多项式f(x)=c0+c1x+…+cnxn为联接多项式的n级线性移位寄存器所产生的非零序列a的周期为2n－1，便称序列a是n级最大周期线性移位寄存器序列，简称m序列。

m序列具有良好的平衡性、游程特性，它的自相关函数具有很好的δ(t)函数特征，所以，m序列具有很好的伪随机特性。

1.2 m子序列

第一类m子序列是在m序列线性反馈函数所确定状态转移图上，修改一定的状态后继，将会在保留原状态转移图主构架基础上，形成一个新的状态转移图，这个新的状态转移图对应一个新的移位寄存器，这个新的移位寄存器所产生的序列就是m子序列，其总的状态数目也是2n－1。

m序列移位寄存器反馈函数式如式(1)，若改变状态转换，其反馈函数也随之改变。

根据参考文献［1］，m序列反馈函数在四点处完成模2加1就能形成m子序列。所以m子序列的反馈函数f'(x)的形式如下:

m子序列移位寄存器是基于m序列移位寄存器，且进行了一定的状态重组，其循环状态也是2n－1个非零状态，所以m子序列的平衡性、游程特性和自相关特性都很好。

2 m子序列的线性复杂度

线性复杂度及其稳定性的研究是评价序列不可预测性的重要指标，序列的线性复杂度不仅要足够大，而且必须有很好的稳定性。由线性复杂度的定义可知［2］:对于非线性序列，其等效线性移位寄存器的长度为该序列的线性复杂度，在已知N长二元序列a0，a1，a2，…，aN－1的情形下，求取这样一个等效线性移位寄存器的长度，采用Berrekamp－Messey算法来完成。该算法的核心思想是运用数学归纳法求出一系列线性移位寄存器。

对于一个GF(2)上的多项式:

其中c0=1，但并不限定c1=1。我们把以f(x)为联接多项式的l级线性移位寄存器简记为＜f(x)，l＞。如果递归关系:

成立。我们就说＜f(x)，l＞产生二元序列a0，a1，a2，…，aN－1。B－M算法的流程图如图1所示:

根据线性复杂度定义，设a=a0a1a2…a1－1是一n级m序列，则n级m序列线性复杂度是n。同一周期(p=2n－1)的m子序列的线性复杂度较m序列的线性复杂度大的多，应用B－M算法可以计算出第一类m子序列的线性复杂度。对最高次数n取7～10的各m序列本原多项式(文献［2］中的附表三)所确定的式(1－2)的m子序列进行了线性复杂度的统计，部分结果如表1所示。

由表1可知:m子序列的线性复杂度比m序列的线性复杂度大的多，逼近于序列周期的一半，正好符合文献［3］中对于密钥序列的要求。

表1 具有同一周期的m序列和m子序列线性复杂度Tab.1 The linear complexity of m sequence and m subsequence which have the same period length

3 m子序列的非线性度

为了抵抗各种攻击，流密码和分组密码算法中所用的m序列必须满足一些密码学准则，比如具有相关免疫性，有高的非线性度。我们知道，m序列是由线性移位寄存器产生的，LFSR的反馈函数是线性函数，它的非线性度为零，所以m序列抵抗线性攻击的能力不强。接下来我们分析m子序列的非线性度。

布尔函数f(x)的Walsh变换，也称Walsh谱，是研究布尔函数非线性度的有力工具。

设f(x)是上的布尔函数，称

为f(x)在ω处的Walsh谱，其中ω·x代表ω与x的内积，即:

设f(x)是上的布尔函数，f(x)的非线性度(Nonlinearity)，记为Nf，等于它与所有线性函数的汉明距离的最小值，即:

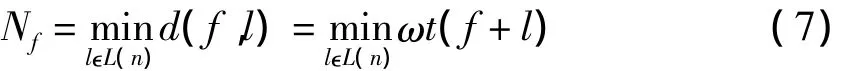
布尔函数的非线性度与Walsh谱之间存在如下的关系:

因此要求出一个布尔函数的非线性度，只要求出其绝对值最大的Walsh谱值即可。

根据参考文献［1］在m序列状态转移图的基础上修改一定的状态后继得到m子序列的反馈函数f'(x)，根据公式(5)和(8)可以计算出反馈函数f'(x)产生的m子序列的Walsh谱值和非线性度的值。图2是9位的m序列交换不同对数的共轭状态得到的不同的m子序列的非线性度Nf的值。

m序列是线性序列，通过计算可知任何m序列的非线性度都是零。m子序列是非线性序列，m子序列的|Wf(ω)|的最大值比m序列的要小一些，而且m子序列的Wf(ω)的非零值的个数要多一些。根据图2可知，相同位数的不同m子序列，交换序列共轭状态的对数越多，得到的m子序列的非线性度越大。因此m子序列和m序列相比，非线性度有了很大的提高，m子序列用来抵抗相关攻击的能力要强的多。

4 结论

m子序列和m序列一样具有周期长、游程性、平衡性和良好的相关性，研究结果表明m子序列的线性复杂度比m序列的线性复杂度大的多，其非线性度和m序列相比也有了很大的提高，因此m子序列是好序列，可以广泛用于密码序列系统中。

［1］吕虹，段颖妮，管必聪，等.第一类 m子序列的构造［J］.电子学报，2007，35(10):2029 －2032.

［2］肖国镇，梁传甲，王育民.伪随机序列及其应用［M］.北京:国防工业出版社，1985.

［3］杨义先，林须端.编译密码学［M］.北京:人民邮电出版社，1992.

［4］CUANG LONG.Crypftographic properties of the welchgong transformation sequence generators［J］.IEEE Transactions on Inforrnation Theory，2002，48(11):2837－2846.

［5］NO J S，CHUNG H，YUN M S.Binary pseudorandom sequences of period 2n －1 with ideal auto correlalation［J］.IEEE Trans IT，1998，44(2):814 － 817.

［6］程郁凡，洪福明.跳频码序列复杂度与随机性分析［J］.电子科技大学学报，1996，25(9):351－357.

［7］武传坤.布尔函数非线性度的谱分析［J］.电子科学学刊，1996，18(5):487 －494.

［8］胡斌，金晨辉，邵增玉.密码学中3类具有特殊Walsh谱值布尔函数的关系［J］.通信学报，2010，31(7):104－109.

［9］朱华安，谢端强.基于m序列统计特性的序列密码攻击［J］.通信技术，2003，8(140):96－98.