玻璃幕墙主要受力杆件结构经济合理性研究
2015-03-18姚贵英徐进云
姚贵英,徐 思,徐进云
(1.河北工程大学 机电工程学院,河北邯郸056038;2.中信渤海铝幕墙装饰工程有限公司,北京100000)
随着我国城镇化的快速推进及建筑行业的快速发展,建筑幕墙就在这样的社会环境中应运而生,并且发展迅猛。中国建筑幕墙行业相关统计数据表明:2006年至2011年,中国幕墙行业实现了总产值翻了三番的巨大效益。2012年,幕墙行业总产值为2200亿元,直到2013年,中国建筑装饰协会颁布了《中国建筑装饰行业“十二五”发展规划纲要》,计划在2015年幕墙行业产值要达到4000亿元。根据幕墙工程量日益增加的情况,加强节能节材减排技术,将进一步推动幕墙行业发展[1]。在幕墙设计过程中,铝型材在幕墙材料中约占35%,而主要受力杆件立柱约占铝型材总量的2/3,因此对于立柱的经济合理性设计应给予高度重视。本文针对主要受力杆件的力学模型选择及理论计算、立柱如何经济合理化设计等方面进行分析并给出意见。
1 立柱力学模型分析
1.1 简支梁
幕墙立柱的实际构造是立柱与主体结构通过一处或两处连接件相连接,每层立柱在与主体结构的连接支座位置向上挑出一段,上下两根立柱通过插芯连接。采用简支梁力学模型就是将只有一处连接件的立柱结构简化为支撑在楼层间的简支梁,以楼层高度作为跨度,按简支梁计算弯矩与剪力,跨中存在最大弯矩,支座处存在最大剪力[2]。但在实际简支梁力学模型中,由于每个楼层只有一个支座,故设计计算立柱时必须取两个支座反力之和[3]。但当幕墙结构嵌入于主体结构中时,只能选择简支梁力学模型进行计算。简支梁力学模型及受力简图见图1。
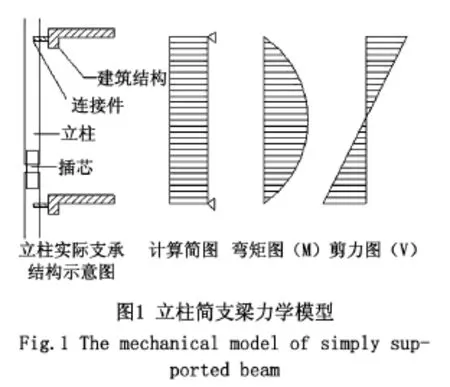
1.2 双跨梁
与简支梁不同的是,每层楼板连接处的混凝土梁上设置两个支座,上支座支承点采用圆孔连接,下支座支承点采用长圆孔连接,此时将这样的连接结构简化双跨梁力学模型进行计算,将上支座支承点设置为固定铰支座,下支座支承点设置为滑动铰支座。
当具备以下两个条件时,应首先考虑选择双跨梁力学模型:(1)幕墙跨度较大,分格较宽时,这时候若选择简支梁需要较大的截面,造成极大的浪费。(2)幕墙龙骨短跨长度a1与幕墙跨度L的比值大于等于0.1时,经公式计算当L2/L≤0.1时,会使中间支座处产生较大的集中应力,造成安全隐患。双跨梁力学模型及受力图见图2[4]。

1.3 连续梁
连续梁力学模型是指在幕墙立柱结构中每楼层混凝土结构上有一个连接支座,上下两根立柱在连接处需要有接头,弯矩需要被有效的传递,此时需要满足(1)套筒插入立柱后其接触面应不小于80%(2)套筒插入立柱的长度应大于2倍的立柱截面高度(3)套筒截面参数(如惯性矩,截面抵抗矩)应大于立柱对应值(4)连接两立柱的套筒在设计和装配时,保持套筒能够有效地传递弯矩。由于在实际施工过程中很难满足所有的要求,经常会选择乘以一个折减系数保证安全,这样的设计不科学也不经济。
1.4 多跨铰接梁
在《玻璃幕墙工程技术规范条文说明》中对规范中6.3.4 ~6.3.6 归纳出“只有当芯柱的惯性矩与外柱相同或者较大且插入足够深度时,才能认为是连续的,否则应按铰接考虑。因此大多数实际工程,应按铰接多跨梁来进行立柱的计算”。
多跨铰接梁力学模型是将立柱的实际结构看做一段段带悬挑的简支梁用铰连接成多跨梁(由于连接插芯不能完全紧固在立柱上,不能传递弯矩,故按铰处理)。由于这种力学模型考虑到各跨之间的连续作用,因此更准确的反应了幕墙立柱的实际受力情况。在多跨铰接梁力学模型计算中,考虑到各个跨之间的影响作用,在计算时从起始梁开始分析。这里仅列出等跨多跨静定梁的计算公式,若不等跨,则需要逐跨分析计算。多跨梁力学模型及受力图见图3。按照支座数量多少,多跨铰接梁又有单支座、双支座之分。其中单支座多跨铰接梁力学模型由于其较双支座多跨铰接梁力学模型受力简单,便于分析,故下面仅对该模型进行理论计算。等跨单支座多跨铰接梁力学模型见图4。

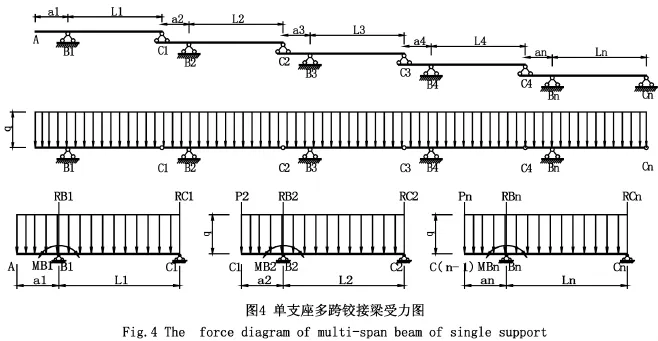
根据受力分析,第一跨的跨中弯矩和第二跨B2支座弯矩为最大,因此主要验算这些截面的受力情况[5-7]。

1)支反力计算。当n≥4以后,RCn逼近一定值,近似取为

式中RC1、RCN-第一跨支反力、第n跨支反力(N);Pn-第n跨集中力(N)。
2)弯矩计算。

式中M1、MB2、Mn-分别为第一跨跨中弯矩、第二跨B2支座弯矩、第n跨跨中弯矩;P2-第2跨集中力(N)。
3)挠度计算。


式中df1中、dfc1、df1、dfn中、dfnc、dfn- 分别为第一跨跨中挠度、第一跨C1支座挠度、第一跨总挠度、第n跨跨中挠度、第n跨Cn支座挠度、第n跨总挠度(mm)。
4)剪力及抗剪计算。
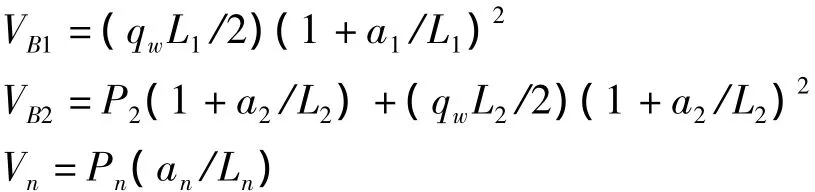
式中VB1、VB2、Vn-分别为第一跨B1支座剪力、第二跨B2支座剪力、第n跨跨中剪力(N)。
5)计算材料截面设计最大应力值及剪力值。

2 应用实例分析
天津某研发中心幕墙设计数据如下:楼层层高L=4 000 mm;用于强度计算时,采用Sw+0.5SE设计值组合q=2.15 N/mm;用于挠度计算时,采用Sw标准值qk=1.39 N/mm;所选型材型号为M2763,材料弹性模量E=70 000 N/mm2;型材抗弯强度设计值fa=135 MPa,型材抗剪强度设计值τa=75 MPa。
2.1 按简支梁力学模型计算
立柱在组合荷载作用下的弯矩设计值

立柱抵抗矩计算
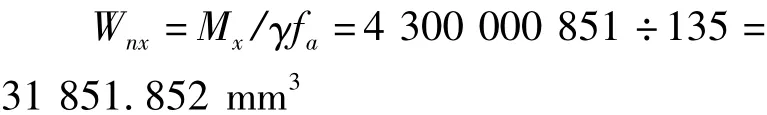
立柱所受剪力设计值组合

2.2 按单支点等跨多跨铰接梁力学模型计算
为了求得最优解以给予实际工程帮助,根据上述单支座多跨铰接梁计算公式,经MATLAB计算机程序编程计算,可得表1和表2。
由表1及表2计算数据的分析结果如下:
1)与简支梁力学模型计算结果相比较,选用单支座等跨多跨铰接梁力学模型可节约:100%≈35.581%,根据;可知弯矩M与截面抵抗矩W成正比关系,可得应用单支座多跨铰接梁力学模型进行立柱设计计算约可节约30%的截面惯性矩,可以取得较好的经济效果。
2)当悬挑梁与简支梁比例a1/L1增大,支反力RC1、RCN逐渐变小、跨中弯矩M1及Mn逐渐变小、支座弯矩逐渐变大。当a1/L1=1/20时,与简支梁弯矩计算值M相比较,可节约100%≈9.76%此时节约量较小,不能产生较好的节约效果,故不建议将悬挑梁与简支梁长度比例设计的过小。但当a1/L1≥1/4时,第二跨支座弯矩MB2与其余跨Mn的弯矩相差过大,并且不适用于幕墙的实际情况,故不予考虑。
3)当a1/L1=1/6~1/5时,立柱的支座负弯矩与跨中正弯矩的绝对值比较接近,并且此时可选取比简支梁力学模型更小的立柱截面系数,达到优化设计的目的。建议在幕墙立柱设计过程中主要选取此合适比例进行安装及计算。
2.3按多跨铰接梁力学模型计算
在上述单支座等跨梁多跨铰接力学模型计算过程中可以观察出,大部分弯矩计算结果由第一跨的跨中弯矩M1起到控制作用,用起始梁的弯矩计算进行杆件设计,节约效果并不是很明显,不能产生最佳的经济效果,不能合理的利用多跨铰接梁的力学模型特点和优势,根据表1调整悬挑段与简支段之比:根据上表令a1/L1≥1/4,其他悬挑段与简支段比值取为1/6。采用第一跨800+3 200=4 000,其余跨550+3 450=4 000。计算如下:

表1 剪力及弯矩计算值(a1/L1=1/30~1/9)Tab.1 The calculation of the shear force and the bending moment(a1/L1=1/30 ~1/9)

表2 剪力及弯矩计算值(a1/L1=1/8.5~1/3)Tab.2 The calculation of the shear force and the bending moment(a1/L1=1/8.5 ~1/3)

通过单支座不等跨梁多跨铰接力学模型与简支梁力学模型计算结果相比较,选用前者可节约:,比单支座等跨梁多跨铰接力学模型更为节约材料。因此,不等跨多跨铰接梁力学模型是一种节材、降低支座安装数、降低人工费用的立柱力学模型设计方法。建议结合混凝土梁实际情况并根据本文的分析计算方法及结论进行优化选择。因此,采用不等跨多跨铰接梁力学模型进行立柱设计可以达到节材、降低支座安装数、降低人工费用等效果。建议在幕墙设计计算过程中,结合混凝土梁实际情况并根据本文的分析计算方法及结论进行优化设计。
3 结语
现阶段大部分工程为了方便仍直接选择最简单的力学模型进行立柱设计计算,并不深入的考虑实情从而大量浪费材料,建议根据本文分析结果,根据主体结构尽量选择多跨铰接梁力学模型进行立柱设计计算,并根据实际混凝土结构合理安装节点位置以达到节材、节能的效果。
[1]黄圻.把握机遇调结构,提高质量增效益[R].广州:中国建筑结构金属协会铝门窗幕墙编委会,2013.
[2]刘伟,刘斌.青岛城市高层建筑楼顶形式特点的解析[J].河北工程大学学报:自然科学版,2011,28(4):51-54.
[3]JGJ102-2003,玻璃幕墙工程技术规范[S].
[4]GB50009-2001,建筑结构荷载规范[S].
[5]张蕾,田炯,李树娜,等.幕墙中双跨梁模型的计算方法[J].门窗,2011(01):16-19.
[6]张芹.建筑幕墙立柱优化设计[A]//2007年全国铝门窗幕墙行业年会论文[C].广州:中国建筑结构金属协会铝门窗幕墙编委会,2007:280-283.
[7]陆新晓,谢云飞.玻璃幕墙建筑的火灾特性[J].黑龙江科技学院学报,2011,21(4):317-320.
