NPSO-GRNN在城市生活需水量预测中的应用
2015-03-18李万庆孟文清
李万庆,王 静,孟文清
(1.河北工程大学 经管学院,河北邯郸056038;2.河北工程大学土木学院,河北邯郸056038)
随着我国城镇化的推进,居民对生活条件的要求不断提升,从而导致水资源的消耗量越来越大,特别是北方的大中型城市,因此,对城市生活需水量进行科学合理的分析预测,不但可以满足居民对水资源的需求,而且可以保证供水系统的正常运行。综合国内外研究现状,我们发现传统的预测模型中存在忽视影响需水量测算因素之间的动态关系,或样本数据量不足等诸多缺陷。例如,常淑玲等[1]通过指数模型和移动平均数法来构建城市需水量综合动态模型,这种方法忽略了需水量各个影响因素之间的动态相互制约关系。张雅君等[2]选用多元线性回归分析法,对影响北京城市生活需水量的因素进行探讨,但该方法受到了显著性检验的制约,选定的自变量只有在通过显著性检验的前提下才能建立回归方程,计算量较大。随着科学和计算机技术的不断发展,新的人工智能方法,如BP神经网络算法,在需水量预测领域得到了广泛的应用[3-5]。但该算法容易陷入局部极小值,收敛性差,给实际应用带来了一定的限制。
针对传统预测方法在需水量预测方面存在的不足,本文尝试将NPSO算法引入到GRNN神经网络中,建立NPSO-GRNN神经网络预测模型,希望能为未来城市生活需水量规划提供参考依据。
1 需水量预测模型
1.1 GRNN 模型
GRNN作为径向基神经网络的一个分支,在1991 年,由美国学者 Donald F.Specht提出[6-7]。
GRNN网络结构由四层构成,如图1所示。

GRNN由输入层、模式层、求和层和输出层四层网络构成。对应网络输入为X=[x1,x2,…,xn]T,输出为Y=[y1,y2,…,yk]T。
输入层。学习样本中输入向量的维数和输入层神经元的数目是相同的,各神经元是简单的分布单元,将输入变量直接传递给模式层。
模式层。学习样本的数目和该层神经元数目是相同的,每个神经元对应不同的学习样本,该层神经元传递函数为

式中X-网络输入变量;Xi-第i个神经元对应的学习样本;σ-光滑因子。
求和层。对求和层进行求和时应用两种类型的神经元。
第一类计算公式为

式中对所有的模式层中的神经元的输出算术求和,模式层与各神经元的连接权值为1,传递函数为
第二类计算公式为

式中对所有模式层中的神经元加权求和,模式层中第i神经元和求和层中第j个分子求和神经元之间的连接权值是第i个输出样本Yi中的第j个元素,传递函数为
输出层。输出层中神经元数目等于学习样本中输出向量的维数k,各神经元把求和层的输出相除,神经元j输出对应估计结果(x)的第j个元素,即
1.2 NPSO 算法
粒子群算法最初是由美国社会心理学家Kennedy和电气工程师Eberhart在1995年共同提出的[8]。在粒子群算法中,我们将每个个体看做是一个在D维搜索空间中不存在质量和体积的粒子,并且拥有飞行速度[9-10]。该算法中粒子的速度和位置进化方程分别为

式(4)和式(5)中υj(t)-粒子j在第t代的速度;ω-惯性权重;c1-认知系数;r1,r2-服从均匀分布的随机数;pj(t)-粒子j的个体历史最优位置;xj(t)-粒子j在第t代的位置;c2-社会系数;pg(t)-群体历史最优位置,xj(t+1)-粒子j在第t+1代的位置。
2002年,Brits在粒子群优化算法中引入了小生境技术,提出了NPSO算法。为保持粒子群的多样性,如果某个粒子在运算连续多次迭代中对应的适应值变化量很小,则以此粒子为中心,以此粒子与其最近的粒子的距离半径构造一个圆形小生境[11]。将小生境粒子群的半径定义为

式中xsj,g- 子粒子群Sj中的最优粒子;xsj,i- 子粒子群Sj中任一非最优粒子。
算法有两个核心操作:(1)如果粒子xi进入子粒子群Sj的范围内,即‖xi-xsj,i‖≤Rs,则此小生境粒子群将会把该粒子吸收;(2)如果两个子粒子群Sj、Sk的范围相交,即‖xi-xsj,i‖≤|Rsj-Rsk|,则两个子粒子群将被合并成一个。
1.3 NPSO-GRNN需水量预测具体步骤
步骤1种群初始化及参数初始化设置,粒子规模 N,认知系数和社会系数c1、c2,迭代终止条件。
步骤2鉴于影响需水量预测的各个因素的量纲和数量级不同,要先对原始数据进行归一化处理再进行训练。本文对原始数据应用比例压缩法进行处理,公式如下:

式中X-原始数据;Xmax-原始数据的最大值;Xmin-原始数据的最小值;T-变换后的数据,也称之为目标数据;Tmax,Tmin-目标数据的最大值和最小值。
步骤3确定适应度函数:把训练样本的输出值与实际值的均方差F看做适应度函数寻找最优σ[12]。适应度函数为

式中yi-实际值,-计算值。训练样本的F越小,越有利于算法迭代停止。
步骤4将学习样本和粒子带入GRNN。
步骤5对每个粒子的适应值进行计算,对最优的适应值和个体进行保留,检验是否满足优化条件,如果满足误差精度,则结束。否则,进入下一个粒子的小生境群体进行优化,全局极值对应的粒子种群当前的最优解为GRNN的光滑因子。
步骤6若最优值没有寻找到,则对每个粒子的小生境群体保留的最优个体组成新的群体空间,重新确定小生境种群个体,重复步骤(4)。
步骤7通过小生境粒子群算法优化后,算法终止时,全局极值点的位置对应的值即是需水量预测GRNN模型中的光滑因子的取值,将其代入GRNN模型中进行训练学习,就可以用来进行预测模型的求解。
2 模型应用实例分析
2.1 数据来源及分析
通过筛选《北京统计年鉴》中提供的相关用水资料,1988—2012年北京市城市生活用水量相关数据如表1所示。
本文依据表1中1988—2012年影响城市生活需水量的城镇人口、第三产业产值、人均居住面积、人均可支配收入作为NPSO-GRNN的输入,输出则为城市生活需水量,网络训练样本为1988—2007年的15组数据,网络预测检验样本为2008—2012年的5组数据。

表1 北京市1988—2012年城市生活用水量相关数据表Tab.1 The related data tables of urban domestic water consumption in Beijing from 1988 to 2012

表2 NPSO-GRNN和BP神经网络训练结果及对比分析Tab.2 NPSO-GRNN and BP neural network training results and their comparative analysis
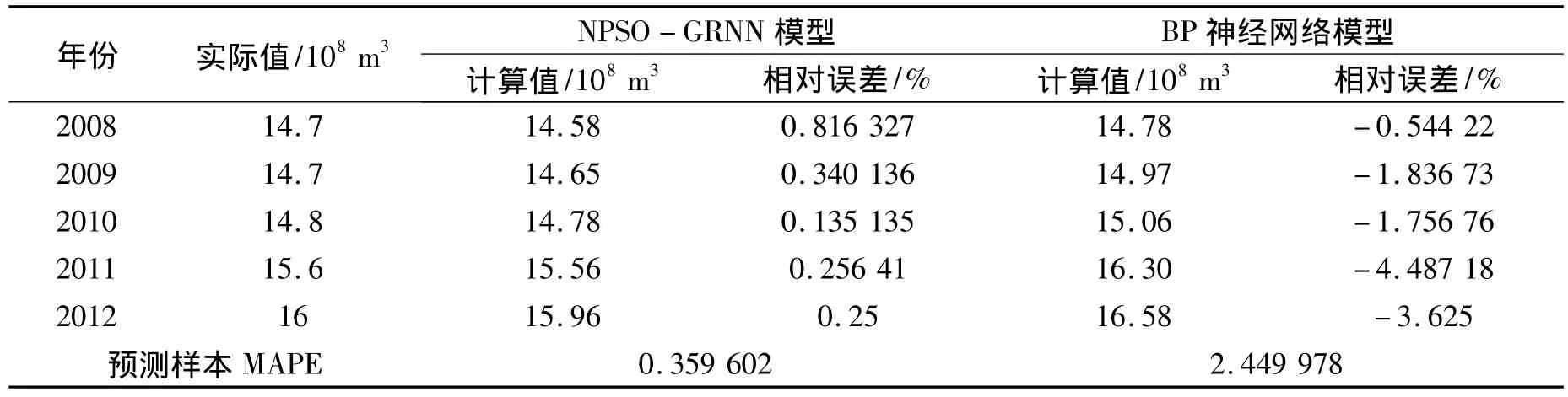
表3 NPSO-GRNN和BP神经网络预测结果及对比分析Tab.3 NPSO -GRNN and BP neural network prediction results and their comparative analysis
2.2 需水预测结果及分析
设置小生境粒子群中粒子规模N=30,认知系数和社会系数c1=c2=2,迭代终止条件为:当训练误差达到10-4或最大迭代次数100。
运用训练好的NPSO-GRNN模型和传统的BP神经网络模型对北京市城市生活需水量进行预测,并以平均相对误差的绝对值MAPE(Mean Absolute Percentage Error)作为衡量预测精度的指标。MAPE的公式为

式中yi-实际值;-计算值。
训练结果和预测结果见表2和表3,相对误差拟合图和训练预测拟合结果见图2。
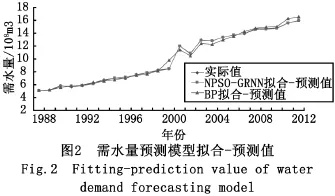
通过分析表2、表3、图2,说明:无论是 NPSO-GRNN模型还是BP神经网络模型,在训练和预测上两个模型的MAPE均控制在了5%以内,达到了较高的精准度。表明:建立的NPSO-GRNN城市生活需水预测模型是可行的,预测的精度高,算法稳定,与BP神经网络模型相比,还具有收敛速度快,不易陷入局部极小值和调整参数少等优势,在实际应用中有很大的前景。
3 结论
1)构建了基于NPSO算法的NPSO-GRNN需水量预测模型,提高了网络的泛化能力和拟合性能。
2)NPSO-GRNN预测模型具有比传统BP神经网络模型预测精度高,不易陷入局部极小值,调整参数少等优点,在实际应用上有良好的前景,为城市生活需水量预测提供了新方法。
[1]常淑玲,尤学一.天津市需水量预测研究[J].干旱区资源与环境,2008,02:14-19.
[2]张雅君,刘全胜,冯萃敏.多元线性回归分析在北京城市生活需水量预测中的应用[J].给水排水,2003,04:26-29.
[3]景亚平,张鑫,罗艳.基于灰色神经网络与马尔科夫链的城市需水量组合预测[J].西北农林科技大学学报:自然科学版,2011(7):229-234.
[4]CUBERO R G.Neural networks for water demand time series forecasting[C].Artificial Neural Networks Int.Workshop,IWANN,1991,453-460.
[5]魏津瑜,苏思沁,施鹤南.基于小波分析的城市需水量预测[J].中南大学学报:自然科学版,2013(Z2):183-187.
[6]黄崇珍,梁静国.基于GRNN的海上钻井平台建造质量预测研究[J].哈尔滨工程大学学报,2009(3):339-343.
[7]陈伟根,奚红娟,苏小平,等.广义回归神经网络在变压器绕组热点温度预测中的应用[J].高电压技术,2012(1):16-21.
[8]李玉军,汤晓君,刘君华.粒子群优化算法在混合气体红外光谱定量分析中的应用[J].光谱学与光谱分析,2009(5):1276-1280.
[9]MATLAB中文论坛.MATLAB神经网络30个案例分析[M].北京:北京航空航天大学出版社,2010.
[10]王晓敏,刘宏伟,李石妍.改进型混沌粒子群算法求解函数均值问题[J].河北工程大学学报:自然科学版,2011,28(3):100-104.
[11]刘文颖,谢 昶,文 晶,等.基于小生境多目标粒子群算法的输电网检修计划优化[J].中国电机工程学报,2013(4):141-148.
[12]李智勇,童调生.基于多种群进化小生境遗传算法的神经网络进化设计方法研究[J].控制与决策,2003(5):607-610.
