基于前景理论的工程建设方案灰靶评价方法
2015-03-19朱玮吴凤平
朱玮,吴凤平
(河海大学商学院,江苏 南京211100)
任何一个工程项目客观上存在多个可行性方案,建设方案的评价是项目可行性研究的重要内容之一,在整个建设过程中具有举足轻重的地位。随着市场经济的不断发展、科技的不断进步,工程的规模在不断的扩大。为了使决策者能对建设方案做出科学合理的选择,有必要采用科学的评价方法对工程建设方案进行评价。目前,许多学者运用熵权法[1]、模糊技术[2]、层次分析法[3-4]等模型方法对工程建设方案的评价方法进行了积极有效的探索,促进了工程建设方案科学评价的进一步发展。但以上学者所采用的评价方法在确定目标权重时,或是主观性较强或是客观性较强;在进行评价过程中计算也较复杂,一定程度上制约了工程建设方案评价结果的有效性,并且,以上方法都是基于决策者绝对理性这一前提条件,忽略了决策者主观上的风险偏好,而这种主观风险偏好往往对最终的决策结果有决定性的影响。同时,由于工程建设方案评价决策环境的复杂性及信息的缺失,决策者往往无法给出效果测度的具体数值,而只能以区间灰数的形式给出。本文针对工程建设方案评价具有的复杂性、不确定性,以及各目标权重无法精确确定的问题,综合考虑决策者思维的模糊性和决策者面临风险所持态度对工程建设方案评价的影响,构建基于前景理论的工程建设方案灰靶评价方法。
1 问题描述
设有n个工程建设方案组成方案集A={A1,A2,…Ai…,An},Ai表示第i个工程建设方案,i=1,2,…,n。有m个影响工程建设方案评价的决策指标为O={O1,O2,…Oj…,Om},Oj表示影响工程建设方案的第j个决策指标,j=1,2,…,m,由此构成工程建设方案Ai对决策指标Oj的效果样本矩阵为x=(xij(⊗))n×m(i=1,2,…,n;j=1,2,…,m)。由于信息的缺失、决策环境的复杂性,决策指标的属性值决策者无法以实际的数值给出,而只能以区间数表示,假设区间灰数表示工程建设方案Ai在第j个决策指标下的效果评价值。其中和分别表示工程建设方案Ai在第j个决策指标Oj下的效果评价值的上限和下限。ωj=(ω1,ω2,L,ωm)为各决策指标的权重向量,且满足
2 模型建立
2.1决策指标的无量纲处理
在实际的工程建设方案评价过程中,为了消除不同决策指标的不同量纲对决策结果的影响,以增加可比性,本文借鉴“奖优罚劣”的思想[5],采用“奖优罚劣”[-1,1]线性变化算子对效果样本矩阵x=(xij(⊗))n×m进行规范化处理,将决策指标分为效益型和成本型两种,规范化过程如下:

(1)对效益型指标
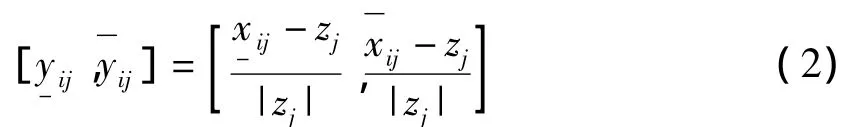
(2)对成本型指标

经过变换后的矩阵记为:Y=(yij(⊗))n×m=,其中y-ij有可能小于 - 1,而有可能大于1。因此,可以采用以下变换方法将矩阵Y=(yij(⊗))n×m规范化:
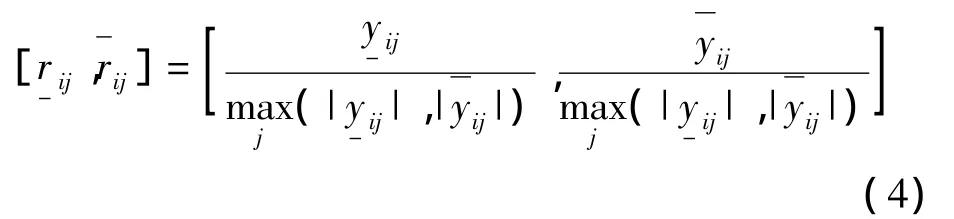
经过上述变化得到工程建设方案Ai对决策指标Oj的效果样本值一致性效果测度矩阵R=(rij(⊗))n×m。
2.2确定正、负靶心及正、负关联系数
参照点的选取是前景理论的核心,决策者在进行决策时,往往会对照参照点来衡量决策的收益或损失。在参照点上,人们更重视预期与结果的差距,而不是结果本身,因此参照点的选取对决策结果有决定性的影响,本文以正、负靶心系数为参照点。
根据规范化后的效果评价值,构建正、负靶心,具体如下:
根据灰靶理论,决策指标的优劣可以通过决策指标与靶心的接近程度来反映。因此,本文利用灰色关联分析方法[6]来计算第i(i=1,2,…,n)个工程建设方案与正、负靶心的正、负关联系数,计算如下:
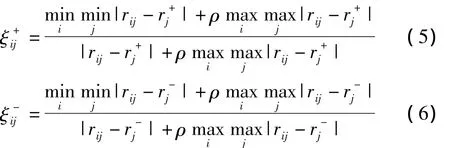
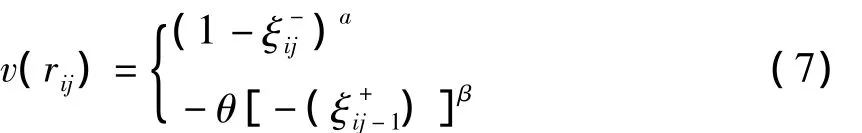
式中,参数α和β分别表示收益和损失区域价值幂函数的凹凸程度,α、β<1表示敏感性递减,θ表示损失区域比收益取悦更陡的特征,θ>1表示损失厌恶,通常取α=0.88,β=0.92,θ=2.25。根据价值函数以负靶心系数为参照点,作为工程建设方案Ai在第Oj个决策指标的正前景值,记为以正靶心系数为参照点,作为工程建设方案Ai在第Oj个决策指标的负前景值,记为为和的距离,且ρ∈[0,1]为分辨系数,一般取ρ=0.5。由此,可以得到正、负关联系数矩阵分别为1,2,…,n;j=1,2,…,m。
2.3 计算价值函数
前景理论主要从收益和损失的角度来分析问题,决策者在面临损失时,往往是追求风险的,在面临收益时,往往是厌恶风险的[7-8]。在工程建设方案评价中,由于影响工程建设方案评价的因素较多,决策者在面临损失时宁愿付出更大的成本以使损失最低。
前景价值是由价值函数和决策权重共同决定的,根据Tversky等[7]在前景理论中给出的价值函数,可以得到工程建设方案Ai对决策指标Oj对应的前景价值函数,即:由此可以得到各工程建设方案的正、负前景矩阵为
设决策者面临收益时的前景权重函数为π+(ωj),面临损失时的前景权重函数为π-(ωj),则工程建设方案Ai的综合前景值为正前景值与负前景值之和,即:
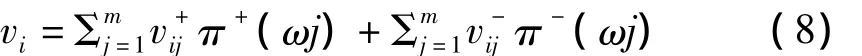
根据文献[8]的研究结果可知:
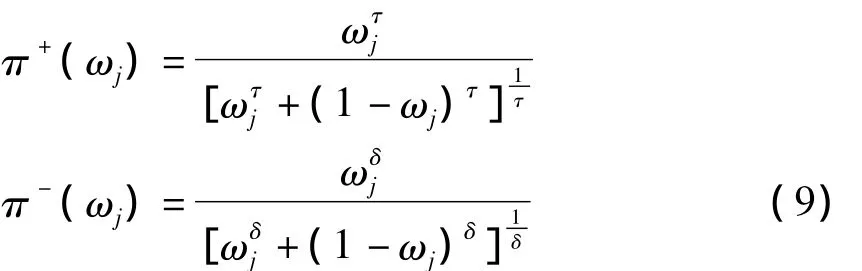
其中,τ为风险损失态度系数;δ为分先收益态度系数,τ=0.61,δ=0.69。
2.4 最优决策指标权重的确定
工程建设方案Ai的不同决策指标Oj的权重向量为ωj=(ω1,ω2,…,ωm)。对于每个工程建设方案Ai来说,其综合前景值越大则建设方案越优,由此可以建立优化模型,其目标函数为:maxV=(V1,V2,…,Vn)。
由于各工程建设方案之间是公平竞争的,因此可以构建优化模型为:
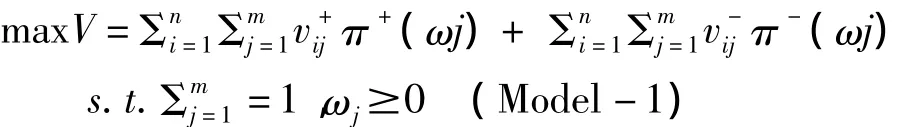
通过Matlab软件编程求解模型(Model-1),可以得到最优解,工程建设方案Ai的最优综合前景值为对每个工程建设方案的最优综合前景值按大小进行排序,便可以排列出工程建设方案的优劣次序。
3 实证分析
某市根据城市规划和经济发展的需要,为方便民众出行,提高交通运输效率,需改建市内一条主干道。通过研究对比,初步筛选出分车道方案A1、快速轨道方案A2、现有道路架设轨道方案A3、混行双层方案A4共4个工程建设方案。该工程建设方案评价指标体系及属性值如表1所示,其中定性指标由专家组打分给出,部分指标取值为实数,计算过程中可视为特殊的区间灰数。
运用基于前景理论的工程建设方案灰靶评价方法,对4个备选方案进行评价,选出最优的方案。
步骤1:采用“奖优罚劣”[-1,1]线性变化算子将效果样本矩阵转化为无量纲化处理的效果样本值一致性效果测度矩阵:
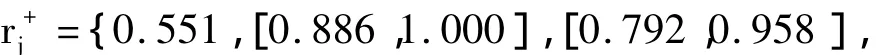


表1 工程建设方案评价的指标体系及效果评价值Tab.1 Evaluation values and indicator system of engineering construction scheme
根据式(5)、(6)计算第i(i=1,2,…,n)个建设方案的正、负关联系数:步骤4:以4个工程建设方案的综合前景值最大化为目标函数,建立优化模型:


然后,运用Matlab编程求解该模型,得到最优解:

4 结论
[1]黄振祥,黄 浩.基于熵权法的建设方案灰理想关联优选[J].价值工程,2014(12):127-128.
[2]沈良峰.基于模糊技术的建筑施工方案则有[J].技术经济,2003(10):61-62.
[3]杨亚文.基于AHP与GRAY的综合评判之公路工程施工方案评价[J].科技信息,2011(3):598-599.
[4]许婧,宋吉荣.建设工程施工方案评价模型的构建分析[J].四川建筑科学研究,2013,39(1):332-335.
[5]党耀国,刘国峰.多指标加权灰靶的决策模型[J].统计与决策,2004,20(3):29 -30.
[6]王正新,党耀国.基于累积前景理论的多指标灰关联决策方法[J].控制与决策,2010,25(2):232-236.
[7]KAHNEMAN D,TVERSKY A.Prospect theory:An analysis of decision under risk[J].Economica,1979,47(2):263-291.
[8]TVERSKY A,KAHNEMAN D.Advances in prospect theory:Cumulative representation of uncertainty[J].Journal of Risk and Uncertainty,1992,5(4):297 -323.
