基于Berkovich压痕的金属材料弹塑性参数 仪器化压入识别方法

陈 伟，马德军，郭俊宏，宋仲康，王家梁

(1. 装甲兵工程学院 机械工程系，北京 100072； 2. 陆军航空兵研究所 信息情报室，北京 101121)

金属材料经过机械加工后，其表层材料的力学性能就会不同于次表层或芯部材料的力学性能，特别是表层材料在强度强化的同时必然伴随着塑性、韧性的劣化。然而受尺寸限制，标准的材料力学性能测试技术及手段无法满足金属表层材料力学性能测试的需要。而用于评价材料局部力学性能的硬度试验，只能 提供金属表层材料的硬度，不能提供关于其强度、塑性及韧性的准确信息。

近年来，在硬度试验的基础上，人们发展了一种新的材料力学性能测试技术-仪器化压入技术[1-2]。仪器化压入技术可以连续同步记录特定几何形状的金刚石压头压入及撤离材料表面的载荷-位移关系，通过力学分析可识别材料的诸多力学性能参数[3-8]。OLIVER等[1]提出了材料弹性模量的仪器化压入识别方法。而相关研究表明，该方法低估了低应变硬化水平材料的真实接触深度，造成弹性模量的高估，最大偏差可达30%[9]。MA等[10-11]提出了用于材料弹性模量仪器化压入识别的“纯能量法”。“纯能量法”在识别金属材料弹性模量时仍存在一定的理论误差，最高为±12.5%[12]，该理论误差源于金属材料应变硬化指数预先未知。利用仪器化压入技术识别金属材料的塑形参数(应变硬化指数和屈服强度)已成为人们研究的热点问题[13-19]。为实现这一目标，建立仪器化压入响应参数与金属材料弹塑性参数间的一一对应关系是关键。DAO等[20]试图利用单一锥形压头仪器化压入所得载荷-位移曲线来识别金属材料的弹塑性参数。然而，相关研究表明，锥顶角固定的锥形压头仪器化压入一组具有不同弹塑性参数组合的材料所得载荷-位移曲线几乎相同，并且根据载荷-位移曲线获得的独立的仪器化压入响应参数仅有两个。这意味着利用单一锥形压头仪器化压入所得载荷-位移曲线无法唯一的识别金属材料的弹塑性参数。基于此，人们将研究焦点转移到两个或者多个具有不同锥顶角的锥形压头上来。目前，基于两个或多个锥形压头建立的金属材料弹塑性参数仪器化压入识别方法可分为两类：间接 法[21-26]和直接法[27-30]。间接法根据载荷-位移曲线确定的仪器化压入响应参数与特征应变和特征应力的无量纲函数关系获得与不同锥形压头相对应的(特征应变和特征应力)数据点，通过数据拟合并结合弹性模量的识别结果来确定金属材料的塑形参数。直接法则直接建立载荷-位移曲线确定的仪器化压入响应参数与金属材料弹塑性参数的无量纲函数关系，以此为基础来识别金属材料的弹塑性参数。CHEN等[31]通过有限元数值仿真对利用两个或多个锥形压头仪器化压入识别材料弹塑性参数的唯一性问题进行了研究。CHEN等[31]发现锥半角为60°到80°的任一圆锥压头仪器化压入一组具有不同弹塑性参数组合的神秘材料，均获得相同的载荷-位移曲线。CHEN等[31]同时指出，神秘材料的神秘性仅针对具有特定角度差的两个圆锥压头来说，如果增加角度差，其神秘性将退去。

上述方法均利用仪器化压入所得载荷-位移曲线来识别金属材料的弹塑性参数。然而，仪器化压入响应除载荷-位移曲线外，还包括压入生成的压痕。相对于载荷-位移曲线，人们针对锥形压头压痕的研究较少见诸报道。TABOR[32]在研究金属材料维氏硬度时发现，对于已经发生充足形变硬化的金属材料，压痕周围材料存在鼓凸现象；对于退火处理的金属材料，压痕周围材料存在沉陷现象。ALCALA等[33]在总结大量维氏硬度试验结果的基础上初步提出了压痕周围材料鼓凸/沉陷程度与材料应变硬化指数之间的函数关系式，在此基础上，ALCALA等[33]指出应变硬化指数约为0.2的金属材料的压痕既不存在鼓凸也不存在沉陷。CHENG等[34]通过有限元数值仿真发现，锥半角为70.3°的圆锥压头压痕周围材料的鼓凸/沉陷程度不仅取决于材料的应变硬化指数，同时取决于屈服强度和弹性模量之比。MATSUDA[35]则通过有限元数值仿真建立了鼓凸情况下的Vickers压痕几何参数及维氏硬度和弹性-线性硬化材料的弹塑性参数之间的无量纲函数关系。MA等[36]针对锥半角为70.3°的圆锥压头仪器化压入CHEN等[31]和CHENG等[34]提出的多组具有不同弹塑性参数组合的材料的压入响应进行了有限元数值仿真。结果表明：虽然同一组内不同材料的载荷-位移曲线几乎相同，但是压痕的鼓凸/沉陷情况却存在较大差别。MA等[36]的研究结果表明仪器化压入压痕和载荷-位移曲线是相互独立的。综上所述可知，作为独立的仪器化压入响应，压痕同样可以提供反映材料力学性能的宝贵信息。因此，根据压痕可引入一个独立的仪器化压入响应参数，结合载荷-位移曲线提供的两个独立的仪器化压入响应参数，可与金属材料的弹性模量、屈服强度和应变硬化指数建立一一对应关系。这从原理上说明了利用单一锥形压头来唯一的识别金属材料的弹塑性参数是可行的。

本文作者选择Berkovich压头用于仪器化压入识别金属材料的弹塑性参数，定义Berkovich压痕中边距与名义中边距之比作为衡量Berkovich压痕鼓凸/沉陷程度的独立的仪器化压入响应参数。本文作者通过量纲分析和有限元数值仿真建立了Berkovich压痕中边距与名义中边距之比、名义硬度及压入比功和金属材料弹塑性参数间的无量纲函数关系，并以此为基础建立了基于Berkovich压痕的金属材料弹塑性参数仪器化压入识别方法，该方法的有效性得到了实验验证。

1 仪器化压入的量纲分析

Berkovich压头的几何形状见图1，根据最大压入深度 hm定义 Berkovich压痕名义中边距。典型的Berkovich压痕如图2所示，定义Berkovich压痕中边距d为Berkovich压痕中心至3个压痕边界距离d1、d2和d3的平均值，即。Berkovich压痕中边距与名义中边距之比d/dn为Berkovich压痕中边距d与Berkovich压痕名义中边距dn的比值。典型的仪器化压入载荷-位移曲线如图3所示，最大压入载荷为Fm，与之相对应的最大压入深度为hm。定义仪器化压入名义硬度，A(hm)为最大压入深度hm所对应的Berkovich压头的横截面积。定义仪器化压入加载功Wt和卸载功We分别为实施仪器化压入时Berkovich压头在加载阶段和卸载阶段所做的功，其值分别等于加载曲线和卸载曲线与仪器化压入载荷-位移曲线横坐标所围面积。仪器化压入比功We/Wt为卸载功We与加载功Wt的比值。

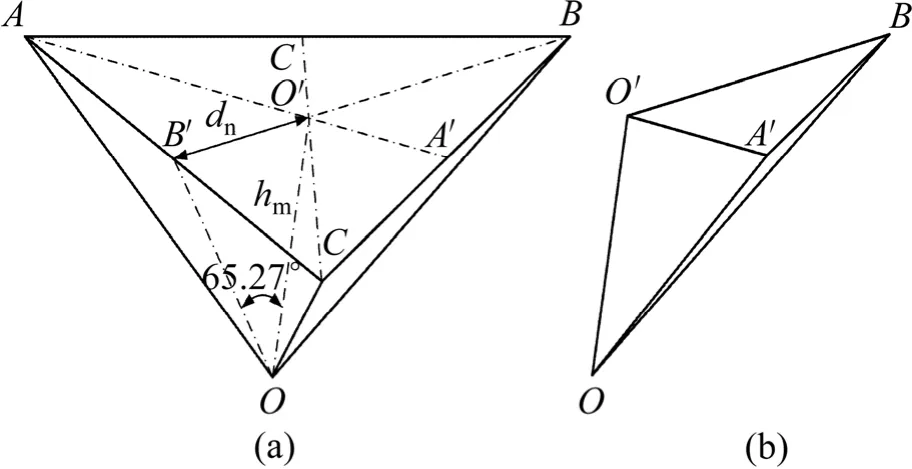
图1 Berkovich压头及其六分之一示意图Fig.1 Schematic illustration of Berkovich indenter(a) and one-sixth(b) for simulation

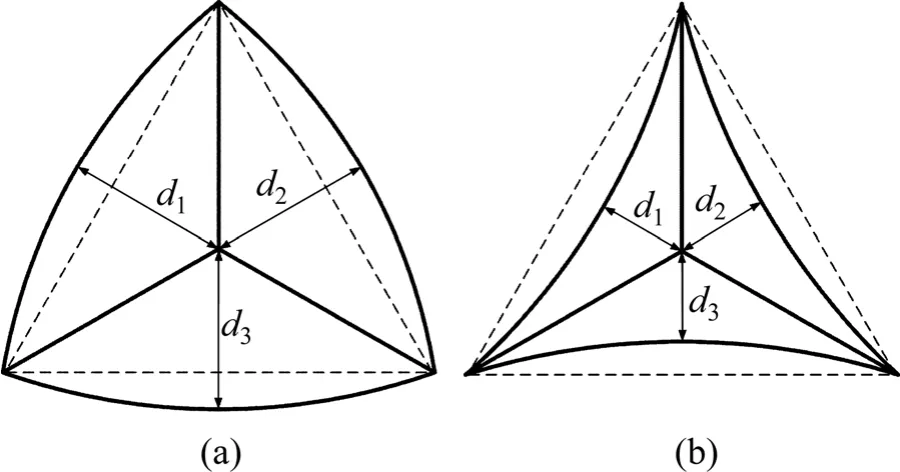
图2 Berkovich压痕示意图Fig.2 Schematic illustration of Berkovich indentation impression with piling-up(a) or sinking-in(b)

图3 仪器化压入载荷-位移曲线及加、卸载功示意图Fig.3 Schematic illustration of load-displacement curves (Wt is total work,We is elastic work)

假设被测材料为均匀、各向同性、率无关的固体材料，且遵循Von Mises屈服准则和纯各向同性强化准则；同时假设被测材料的单轴真实应力-应变关系由线弹性和Hollomon幂硬化函数组成，即

式中：σ和ε为真实应力和真实应变；E为弹性模量；

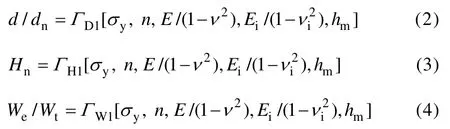
根据式(5)和式(6)，式(2)、(3)和(4)可改写为

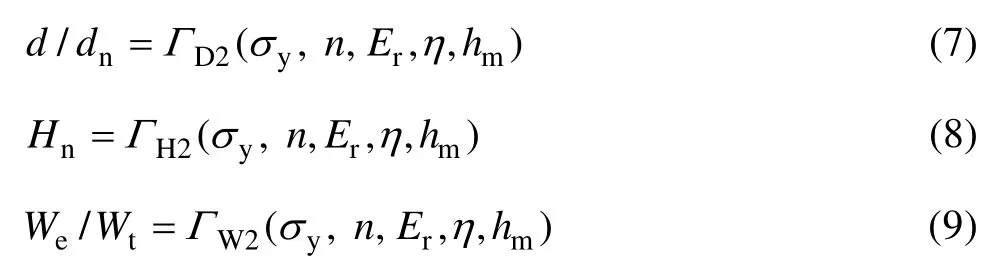
应用量纲∏定理，式(7)、(8)和(9)可简化为

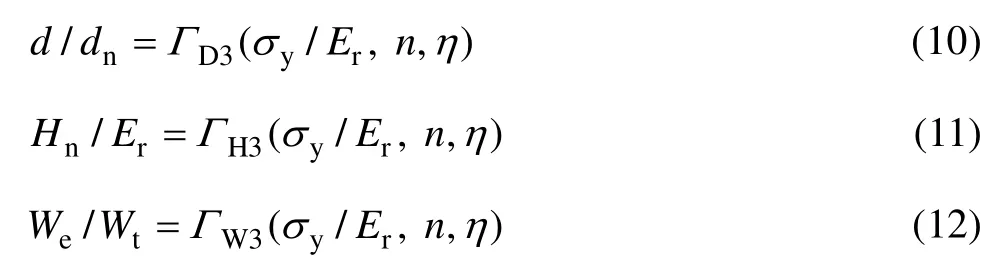
由式(12)可得

将式(13)代入式(10)和式(11)得

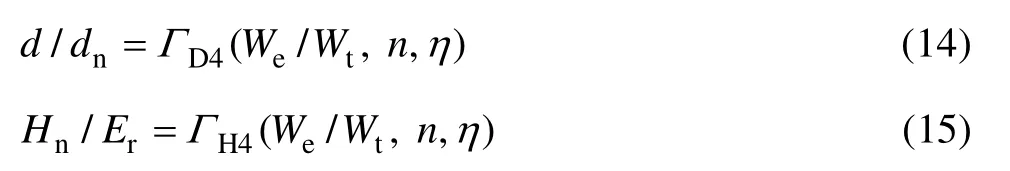
根据式(13)和式(15)可得

2 仪器化压入的有限元仿真

为获得式(14)、(15)和(16)的显示表达式，本文作者应用有限元软件ABAQUS建立三维模型对具有理想形状的金刚石Berkovich压头仪器化压入被测材料的压入响应进行数值模拟。根据Berkovich压头的对称性，选取压头的1/6(ΔO′AB′)及与压头相对应的被测材料的1/6用于有限元仿真，如图1所示。有限元划分的Berkovich压头与被测材料的总体网格和靠近压头尖端的局部网格见图4。Berkovich压头划分了20000个一阶四面体单元，被测材料划分了120000个一阶四面体单元和30000个一阶六面体单元。有限元模型的网格收敛性和远场无关性均符合要求。在图 4(a)内，以Berkovich压头尖点为坐标原点O，定义空间直角坐标系O-XYZ，其中X轴方向为Berkovich压头横截面内压头中心与棱边中心连线方向(图1中O′A′方向)，Z轴方向为Berkovich压头轴线方向，Y轴方向根据右手法则确定。Berkovich压头的弹性模量Ei=1141 GPa，泊松比iν=0.07。被测材料弹性模量E取值为70GPa、200 GPa和400 GPa；屈服强度 yσ的取值范围为1~45000 MPa；应变硬化指数n取值为0、0.15、0.3和0.45；泊松比ν取固定值0.3。 被测材料和Berkovich压头的平面应变弹性模量之比η分别为0.0671、0.1917和0.3834。Berkovich压头与被测材料间的接触摩擦因数取值为0。

图4 Berkovich压头与被压材料有限元网格划分的总体网格和靠近压头尖端的局部网格 Fig.4 FE mesh designs of Berkovich indenter and indented material overall mesh(a) and detailed mesh(b) near tip of Berkovich indenter

仪器化压入卸载后，在XOZ平面内提取Berkovich压痕轮廓，图5(a)显示了一组弹性模量E=200 GPa并具有不同屈服强度σy和应变硬化指数n的材料的压痕轮廓，横坐标为节点到Z轴的距离dZ与最大压入深度hm的比值dZ/hm，纵坐标为节点在Z轴方向发生的位移uZ与最大压入深度hm的比值uZ/hm，负号表示节点位移方向与Z轴正方向相反。进一步确定dZ/hm=tan(65.27°)附近的轮廓曲线曲率半径变化最小处与Z轴的距离为Berkovich压痕中边距d。图5(b)所示为对应于图5(a)所示材料的仪器化压入载荷-位移曲线，可以看出，该组材料的载荷-位移曲线几乎相同。

图5 一组材料的压痕轮廓及载荷-位移曲线 Fig.5 Instrumented indentation responses of a set of materials with distinct plastic properties: (a) Profiles of Berkovich indentation impressions in XOZ plane; (b) F-h curves

图6 所示为有限元数值仿真得到的对应于不同n和η的d/dn-We/Wt关系。可以看出，对于确定的n，η对d/dn-We/Wt关系的影响极为有限。因此，利用多项式函数对n的4个不同取值情况下的d/dn-We/Wt关系进行拟合，结果表示为

图7所示为有限元数值仿真得到的对应于不同n和η的Hn/Er-We/Wt关系。可以看出，对于确定的n和η对Hn/Er-We/Wt关系存在一定的影响，这表明折合弹性模量Er不能准确反映金刚石Berkovich压头和被测材料之间的联合弹性效应。为此，定义联合弹性模量，并替代折合弹性模量Er可得Hn/Ec-We/Wt关系，其结果如图8所示。

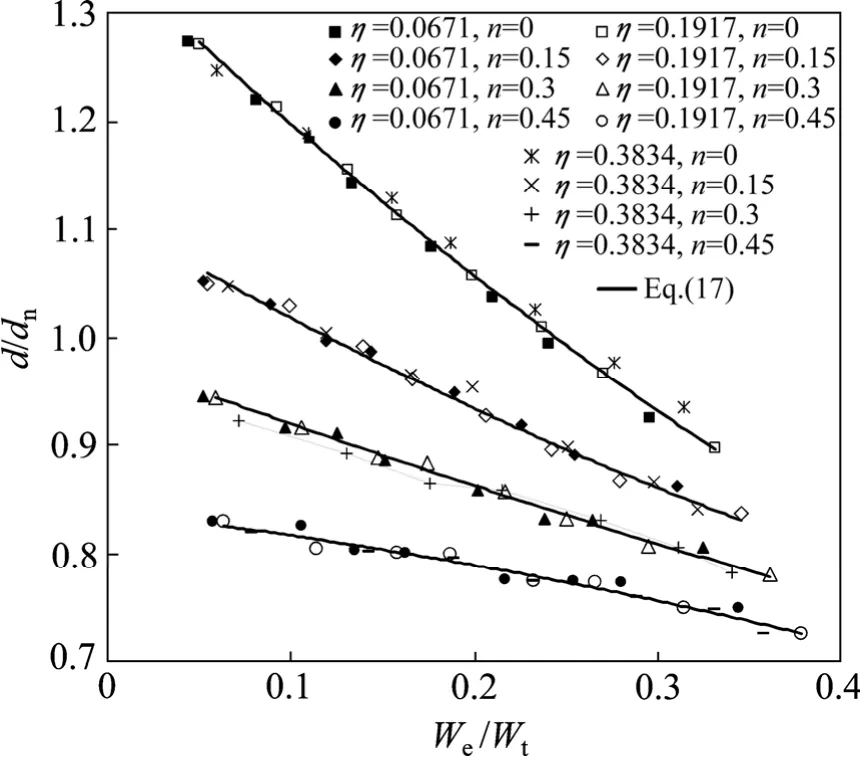
图6 对应于不同n和η的d/dn-We/Wt关系 Fig.6 Plots of d/dn versus We/Wt with different values of n and η

表1 系数aij (i=1,…,4; j=0,1,2)的取值 Table1 Values of aij (i=1,…,4; j=0,1,2)

由图8可以看出，对于确定的n，Hn/Ec-We/Wt关系几乎不受η的影响。因此，利用多项式函数对n的4个不同取值情况下的Hn/Ec-We/Wt关系进行拟合，其关系可表示为

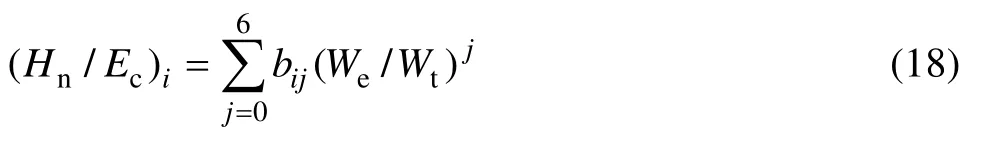
其中，i=1,…,4分别对应n的4个不同取值：0，0.15，0.30，0.45；系数bij(j=0,…,6)的取值见表2。式(18)所代表的n分别取0、0.15、0.30和0.45时的Hn/Ec-We/Wt关系如图9所示。

图10所示为有限元数值仿真得到的对应于不同n和η的σy/Hn-We/Wt关系图。利用多项式函数对σy/Hn-We/Wt关系进行拟合，其关系可表示为

式中：i=1,…,4分别对应n的4个不同取值：0，0.15，0.30，0.45；j=1,2,3分别对应η的3个不同取值：0.0671，0.1917，0.3834；系数cijk(k=0,…,6)的取值见表3。

图7 不同n和η时的Hn/Er-We/Wt关系 Fig.7 Hn/Er-We/Wt curves at different values of n and η: (a) n=0; (b) n=0.15; (c) n=0.30; (d) n=0.45

图8 不同n和η时Hn/Ec-We/Wt关系 Fig.8 Hn/Ec-We/Wt curves at different values of n and η: (a) n=0; (b) n=0.15; (c) n=0.30; (d) n=0.45

表2 系数bij (i=1,…,4; j=0,…,6)的取值 Table2 Values of bij (i=1,…,4; j=0,…,6)

图9 不同n时Hn/Ec-We/Wt关系 Fig.9 Hn/Ec-We/Wt curves at different values of n

3 方法建立

根据关系式(17)、(18)、(19)，本文作者建立基于Berkovich压痕的金属材料弹塑性参数仪器化压入识别方法，具体包括以下步骤：

1) 利用仪器化压入仪和金刚石Berkovich压头对被测材料实施最大压入载荷为Fm的仪器化压入测试，获得载荷-位移曲线，同时利用该曲线确定最大压入深度hm和名义硬度Hn=Fm/A(hm)(不考虑压头尖端钝化时，；考虑压头尖端钝化时，m( )Ah 由金刚石Berkovich压头的面积函数 ()Ah来确定，即

采用自动舵技术，借助螺旋桨的推力和两个螺旋桨的速度差来实时调节航速和航向，实现自动按照预先设定的计划的航线进行精准的走线、换线及回归等功能。

2) 根据载荷-位移曲线的加载部分和卸载部分计算压入加载功Wt和卸载功We，并计算仪器化压入比功We/Wt；

3) 借助显微镜分别量取Berkovich压痕中心至3个压痕边界的距离：d1、d2和d3，并确定Berkovich压痕中边距及其与名义中边距

4) 根据仪器化压入比功We/Wt和关系式(17)确定

图10 对应于不同n和η的σy/Hn-We/Wt关系 Fig.10 Plots of σy/Hn versus We/Wt with different values of n corresponding to (a) η=0.0671,(b) η=0.1917,and (c) η=0.3834

进一步根据非负原则确定被测材料的应变硬化指数n：

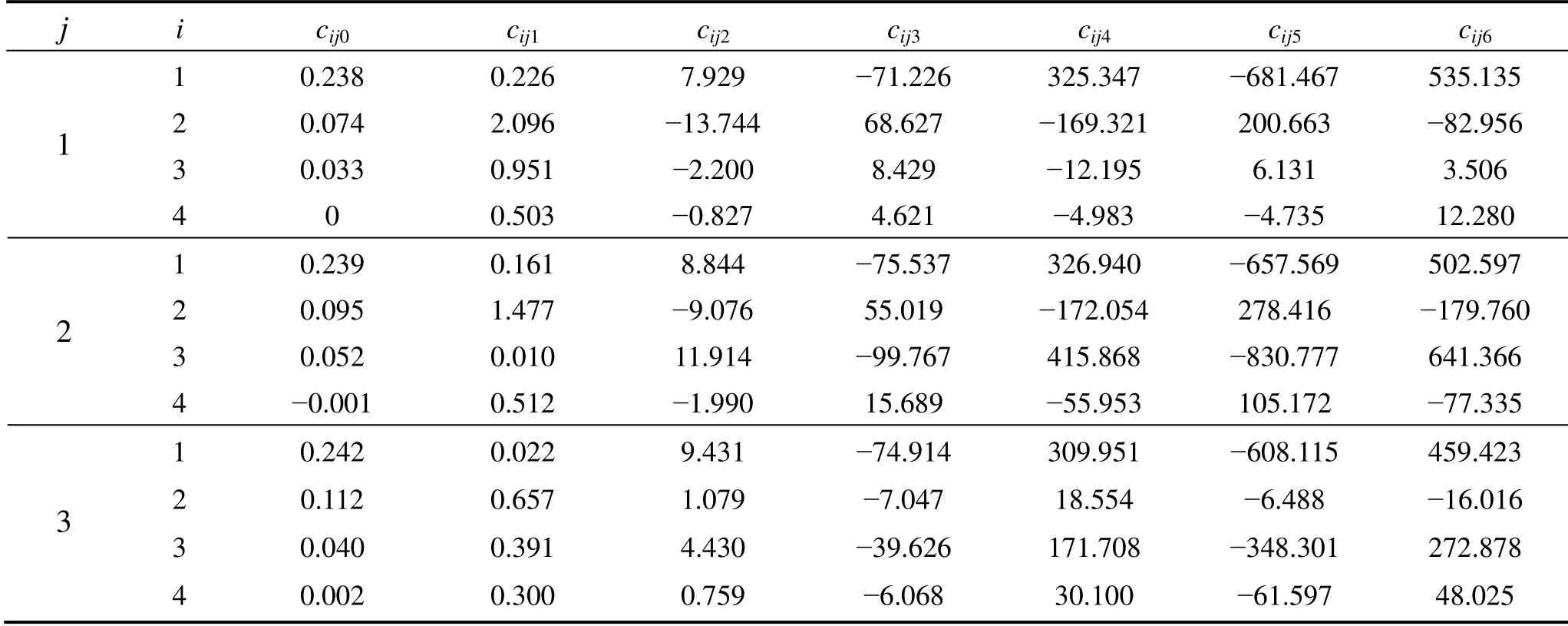
表3 系数cijk (i=1,…,4; j=1,2,3; k=0,…,6)的取值 Table3 Values of cijk (i=1,…,4; j=1,2,3; k=0,…,6)

5) 根据仪器化压入比功We/Wt和关系式(18)确定

根据名义硬度Hn及Hn/Ec值确定被测材料与金刚石Berkovich压头的联合弹性模量Ec：

进而确定被测材料的弹性模量E：

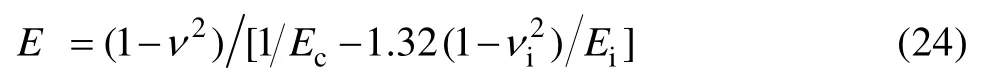
式中：金刚石Berkovich压头的弹性模量Ei=1141 GPa，泊松比iν=0.07，被测材料的泊松比ν可根据材料手册确定。如果被测材料的泊松比ν不能由材料手册确定，则取值为0.3。

6) 根据仪器化压入比功We/Wt及关系式(19)确定

4 实验验证

本实验中选择6061铝合金、S45C碳钢、SS316不锈钢和黄铜4种金属材料用于检验本实验中建立的基于Berkovich压痕的金属材料弹塑性参数仪器化压入识别方法的有效性。4种金属材料的仪器化压入试样呈圆柱状，尺寸为d 10 mm×10 mm，并且测试表面均采用Al2O3研磨膏进行了抛光。利用高精度仪器化压入仪和金刚石Berkovich压头对上述4种金属材料不同区域重复进行5次仪器化压入测试，最大压入载荷设定为50 N，加、卸载速率均为0.3 N/s，最大压入载荷时保载30 s。图11所示为Berkovich压头仪器化压入4种金属材料所得载荷-位移曲线。图12所示为4种金属材料的Berkovich压痕。

图11 Berkovich压头仪器化压入金属材料所得载荷-位移曲线 Fig.11 F-h curves obtained from instrumented indentation experiments with Berkovich indenter of metals: (a) 6061 aluminum alloy; (b) S45C carbon steel; (c) SS316 stainless steel; (d) Brass

图12 金属材料的Berkovich压痕 Fig.12 Berkovich indentation impressions obtained from instrumented indentation experiments of metals: (a) 6061 aluminum alloy; (b) S45C carbon steel; (c) SS316 stainless steel; (d) Brass

根据仪器化压入测试所得载荷-位移曲线及Berkovich压痕，可以分别确定4种金属材料的仪器化压入名义硬度Hn、仪器化压入比功We/Wt及Berkovich压痕中边距与名义中边距之比d/dn，在此基础上，应用本文所建立的方法可确定4种金属材料的应变硬化指数n、弹性模量E、条件屈服强度σ0.2及强度极限σb，结果见表4。为了与标准单轴拉伸试验结果进行比 较，将仪器化压入测试所用6061铝合金、S45C碳钢、SS316不锈钢和黄铜的相同材料分别制成标准单轴拉伸试样，在MTS810通用材料试验机上分别实施两次标准单轴拉伸试验，以两次试验结果的平均值作为单轴拉伸试验的测试结果。由标准单轴拉伸试验测定的6061铝合金的弹性模量EU、应变硬化指数nU、条件屈服强度σ0.2U及强度极限σbU为71 GPa、0.052、299.37 MPa及366.25 MPa；由标准单轴拉伸试验测定的S45C碳钢的弹性模量EU、应变硬化指数nU、条件屈服强度σ0.2U及强度极限σbU为201 GPa、0.176、431.08 MPa及612.84 MPa；由标准单轴拉伸试验测定的SS316不锈钢的弹性模量EU、应变硬化指数nU、条件屈服强度σ0.2U及强度极限σbU为184 GPa、0.134、610.11 MPa及827.51 MPa；由标准单轴拉伸试验测定的黄铜的弹性模量EU、应变硬化指数nU、条件屈服强度σ0.2U及强度极限σbU为83 GPa、0.125、346.67 MPa及421.23 MPa。将6061铝合金、S45C碳钢、SS316不锈钢和黄铜的弹性模量、应变硬化指数、条件屈服强度和强度极限的仪器化压入测试结果与单轴拉伸试验结果进行比较，可以确定仪器化压入测试结果的测试误差：

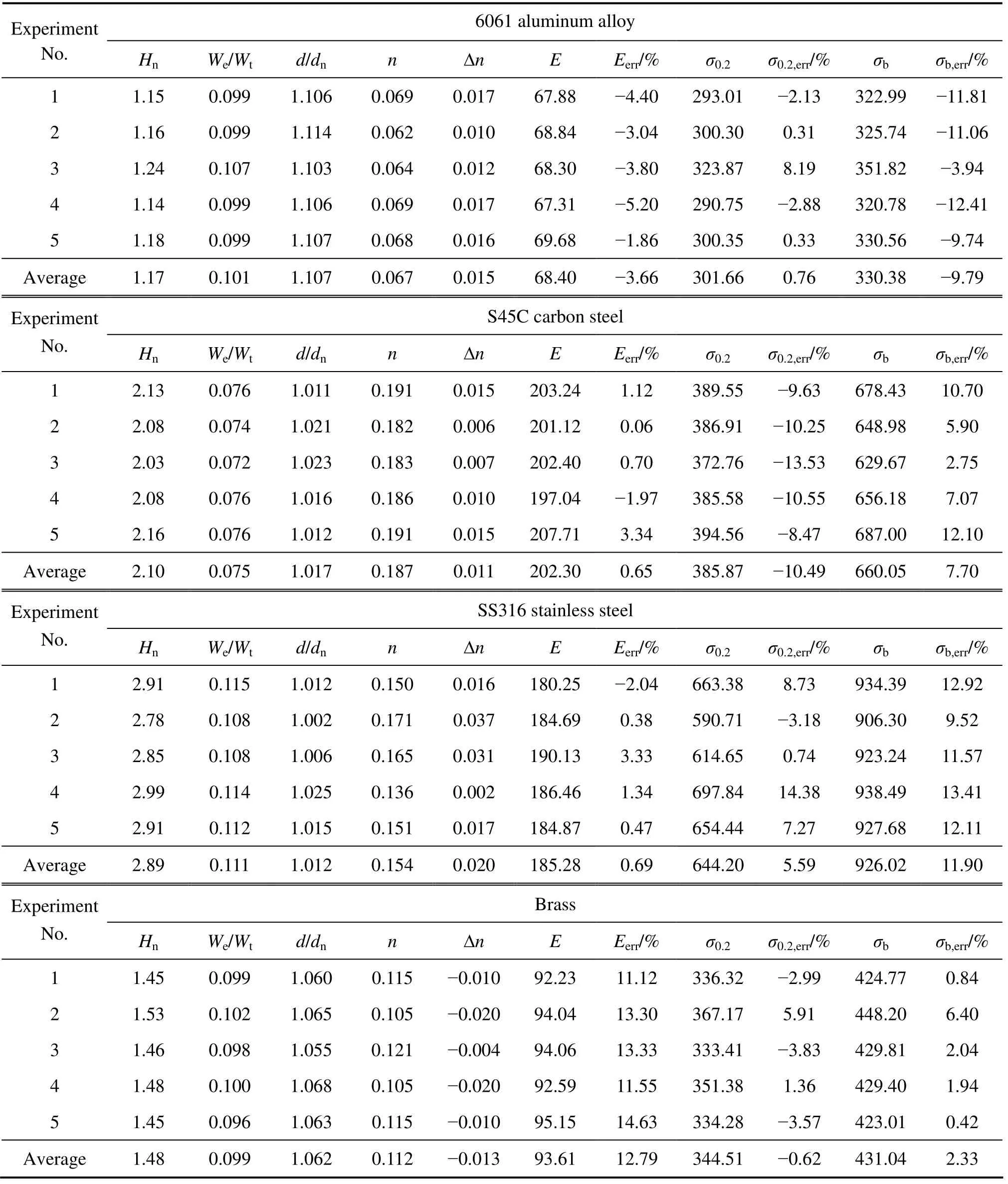
表4 最大载荷为50 N时6061铝合金、S45C碳钢、SS316不锈钢和黄铜弹塑性参数仪器化压入测试结果与测试误差 Table4 Determination results and errors of elastic-plastic properties of 6061 aluminum alloy,S45C carbon steel,SS316 stainless steel and brass at Fm=50 N

图13 金属材料仪器化压入实验所得真实应力-应变曲线与单轴拉伸试验所得真实应力-应变曲线的比较 Fig.13 Comparison between true stress-strain curves determined by instrumented indentation and standard uniaxial tensile tests of metals: (a) 6061 aluminum alloy; (b) S45C carbon steel; (c) SS316 stainless steel; (d) Bbrass

5 结论

1) 提出了一个用于衡量Berkovich压痕鼓凸/沉陷程度的独立的仪器化压入响应参数-Berkovich压痕中边距与名义中边距之比d/dn，应用量纲分析和有限元数值仿真建立了Berkovich压痕中边距与名义中边距之比d/dn、仪器化压入名义硬度Hn、仪器化压入比功We/Wt与金属材料弹性模量E、应变硬化指数n和屈服强度σy之间的无量纲函数关系式，并以此为基础建立了基于Berkovich压痕的金属材料弹塑形参数仪器化压入识别方法。该方法仅利用单一Berkovich压头仪器化压入金属材料所得载荷-位移曲线及Berkovich压痕即可确定金属材料的弹性模量E、应变硬化指数n、条件屈服强度σ0.2及强度极限σb。

2) 与标准单轴拉伸试验结果相比较，应用本文所提方法识别得到的6061铝合金、S45C碳钢、SS316不锈钢和黄铜的弹性模量的相对测试误差分别为-3.66%、0.65%、0.69%和12.79%，应变硬化指数的绝对测试误差分别为0.015、0.011、0.020和-0.013，条件屈服强度σ0.2的相对测试误差分别为0.76%、-10.49%、5.59%和-0.62%，强度极限σb的相对测试误差分别为-9.79%、7.70%、11.90%和2.33%，均满足工程应用要求。

3) 仪器化压入识别得到的4种金属材料的真实应力-应变曲线与标准单轴拉伸试验所得真实应力-应变曲线具有较好的一致性。

4) 6061铝合金、S45C碳钢、SS316不锈钢和黄铜的仪器化压入识别结果验证了该基于Berkovich压痕的金属材料弹塑性参数仪器化压入识别方法是可行和非常有效的。

[1] OLIVER W C,PHARR G M. An improved technique for determining hardness and elastic-modulus using load and displacement sensing indentation experiments[J]. Journal of Materials Research,1992,7(6): 1564-1583.

[2] FISCHER-CRIPPS A C. Nanoindentation[M]. New York: Springer-Verlag,2004.

[3] ZHANG T H,FENG Y H,YANG R,JIANG P. A method to determine fracture toughness using cube-corner indentation[J]. Scripta Materialia,2010,62(4): 199-201.

[4] TRICOTEAUX A,DUARTE G,CHICOT D,BOURHIS L,BEMPORAD E,LESAGE J. Depth-sensing indentation modeling for determination of elastic modulus of thin films[J]. Mechanics of Materials,2010,42(2): 166-174.

[5] 任明星,李邦盛,杨 闯,傅恒志. 纳米压痕法测定微铸件硬度及弹性模[J]. 中国有色金属学报,2008,18(2): 231-236.

RENG Ming-xing,LI Bang-shen,YANG Chuang,FU Heng-zhi. Hardness and elastic modulus of microcastings by nanoindentation[J]. The Chinese Journal of Nonferrous Metals,2008,18(2): 231-236.

[6] 崔 航,陈怀宁,陈 静,黄春玲,吴昌忠. 球形压痕法评价材料屈服强度和应变硬化指数的有限元分析[J]. 金属学报,2009,45(2): 189-194.

CUI Hang,CHEN Huai-ning,CHEN Jing,HUANG Chun-ling,WU Chang-zhong. FEA of evaluating material yield strength and strain hardening exponent using a spherical indentation[J]. Acta Metallurgica Sinica,2009,45(2): 189-194.

[7] 马德军. 材料弹性模量的仪器化压入测试方法[J]. 中国有色金属学报,2010,20(12): 2336-2343.

MA De-jun. Method for determining elastic modulus by instrumented indentation test[J]. The Chinese Journal of Nonferrous Metals,2010,20(12): 2336-2343.

[8] 宋仲康,马德军,郭俊宏,陈 伟. 一种改进的纳米压入测试方法[J]. 中国有色金属学报,2012,22(2): 520-525.

SONG Zhong-kang,MA De-jun,GUO Jun-hong,CHEN Wei. A modified method of nanoindentation testing method[J]. The Chinese Journal of Nonferrous Metals,2012,22(2): 520-525.

[9] BOLSHAKOV A,PHARR G M. Influences of pileup on the measurement of mechanical properties by load and depth sensing indentation techniques[J]. Journal of Materials Research,1998,13(4): 1049-1058.

[10] MA D,ONG C W. Analytical relationship among nominal hardness,reduced Young’s modulus,the work of indentation,and strain hardening exponent[J]. Journal of Materials Science,2010,45(9): 2530-2533.

[11] MA D,ONG C W. Further analysis of energy-based indentation relationship among Young’s modulus,nominal hardness,and indentation work[J]. Journal of Materials Research,2010,25(6): 1131-1136.

[12] 马德军. 材料力学性能仪器化压入测试原理[M]. 北京: 国防工业出版社,2010.

MA De-jun. Principles of measuring mechanical properties of materials by instrumented indentation[M]. Beijing: National Defense Industry Press,2010.

[13] HUBER N,NIX W D,GAO H. Identification of elastic-plastic material parameters from pyramidal indentation of thin films[J]. Proceedings of the Royal Society of London Series A,2002,458: 1593-1620.

[14] BOUZAKIS K D,VIDAKIS N. Superficial plastic response determination of hard isotropic materials using ball indentations and a FEM optimization technique[J]. Materials Characterization,1999,42(1): 1-12.

[15] MULIANA A,STEWARD R,HAJ-ALI R M,SAXENA A. Artificial neural network and finite element modeling of nanoindentation tests[J]. Metallurgical and Materials Transactions A,2002,33(7): 1939-1947.

[16] THO K K,SWADDIWUDHIPONG S,LIU Z S,HUA J. Artificial neural network model for material characterization by indentation[J]. Modelling and Simulation in Materials Science and Engineering,2004,12(5): 1055-1062.

[17] HAJ-ALI R,KIM H K,KOH S W,SASENA A,TUMMALA R. Nonlinear constitutive models from nanoindentation tests using artificial neural networks[J]. International Journal of Plasticity,2008,24: 371-396.

[18] COLLIN J M,MAUVOISIN G,PILVIN P. Materials characterization by instrumented indentation using two different approaches[J]. Materials and Design,2010,31: 636-640.

[19] BOLZON G,TALASSI M. An effective inverse analysis tool for parameter identification of anisotropic material models[J]. International Journal of Mechanical Sciences,2013,77: 130-144.

[20] DAO M,CHOLLACOOP N,VAN K J,VENKATESH T A,SURESH S. Computational modelling of the forward and reverse problems in instrumented sharp indentation[J]. Acta Materialia,2001,49: 3899-3918.

[21] BUCAILLE J L,STAUSS S,FELDER E,MICHLER J. Determination of plastic properties of metals by instrumented indentation using different sharp indenters[J]. Acta Materialia,2003,51(6): 1663-1678.

[22] YAN J,KARLSSON A M,CHEN X. Determining plastic properties of a material with residual stress by using conical indentation[J]. International Journal of Solids and Structures,2007,44: 3720-3737.

[23] CHENG Y T,LI Z,CHENG C M. Scaling relationships for indentation measurements[J]. Philosophical Magazine A,2002,82(10): 1821-1829.

[24] CHOLLACOOP N,DAO M,SURESH S. Depth-sensing instrumented indentation with dual sharp indenters[J]. Acta Materialia,2003,51: 3713-3729.

[25] CAO Y P,QIAN X Q,LU J,YAO Z H. An energy-based method to extract plastic properties of metal materials from conical indentation tests[J]. Journal of Materials Research,2005,20(5): 1194-1206.

[26] OGASAWARA N,CHIBA N,CHEN X. Representative strain of indentation analysis[J]. Journal of Materials Research,2005,20(8): 2225-2234.

[27] SWADDIWUDHIPONG S,THO K K,LIU Z S,ZENG K. Material characterization based on dual indenters[J]. International Journal of Solids and Structures,2005,42: 69-83.

[28] LUO J,LIN J. A study on the determination of plastic properties of metals by instrumented indentation using two sharp indenters[J]. International Journal of Solids and Structures,2007,44(18/19): 5803-5817.

[29] LE M Q. A computational study on the instrumented sharp indentations with dual indenters[J]. International Journal of Solids and Structures,2008,45: 2818-2835.

[30] LE M Q. Improved reverse analysis for material characterization with dual sharp indenters[J]. International Journal of Solids and Structures,2011,48: 1600-1609.

[31] CHEN X,OGASAWARA N,ZHAO M H,CHIBA N. On the uniqueness of measuring elastoplastic properties from indentation: The indistinguishable mystical materials[J]. Journal of Mechanics and Physics of Solids,2007,55: 1618-1660.

[32] TABOR D. The hardness of metals[M]. Oxford: Clarendon Press,1951.

[33] ALCALA J,BARONE A C,ANGLADA M. The influence of plastic hardening on surface deformation modes around Vickers and spherical indenters[J]. Acta Materialia,2000,48: 3451-3464.

[34] CHENG Y T,CHENG C M. Effects of ‘sinking in’ and ‘piling up’ on estimating the contact area under load in indentation[J]. Philosophical Magazine Letters,1998,78(2): 115-120.

[35] MATSUDA K J. Prediction of stress-strain curves of elastic-plastic materials based on the Vickers indentation[J]. Philosophical Magazine A,2002,82(10): 1941-1951.

[36] MA Z S,ZHOU Y C,LONG S G,ZHONG X L,LU C. Characterization of stress-strain relationships of elastoplastic materials: An improved method with conical and pyramidal indenters[J]. Mechanics of Materials,2012,54: 113-123.