基于烟花算法与差分进化算法的模糊分类系统设计

朱晓东，刘 冲，郭雅默

(郑州大学 电气工程学院，河南 郑州450001)

0 引言

模糊分类系统能够融合专家经验，通过易于理解的模糊规则来阐述实际问题的内部机理，因而在模式识别、数据挖掘等领域得到了广泛的应用．为了提高模糊系统的性能，学者们做了大量的研究:利用聚类算法建立模糊模型［1］，采用遗传算法［2-3］或神经网络［4-5］学习模糊规则及隶属函数的特征参数等． 然而，这些算法在追求模型高精确度的同时，采用了较多的模糊规则和模糊集合，使得模型结构复杂、难以理解．为了建立结构简单易懂、精确度高的模糊模型，文献［6］采用分层模糊的概念来构造模糊系统，降低了系统维度，简化了系统的结构． 文献［7］采用基于类空间模糊度的计算几何分类器权重分配方法来构建分类器，这种方法使得模型的精确性和解释性都得到了进一步的提高．

烟花算法［8］是受烟花在夜空中的爆炸现象启发而提出的一种新的群智能算法，和粒子群算法等其他方法相比具有较好的搜索性能． 在烟花算法中，性能较好的烟花在较小的搜索范围内产生数量较多的子代火花，进而加快了收敛速度;而性能较差的烟花则在较大的搜索范围内产生数量较少的子代火花，因而扩大了搜索范围，提高了种群的多样性．但是，烟花算法忽略了不同烟花个体之间的相互联系和学习，这样容易使算法过早成熟．为了解决这个问题，将差分算法与烟花算法相结合，进一步增加种群的多样性，扩大搜索区域，增强个体间的相互联系，防止算法过早陷入局部最优［9］．笔者将烟花算法和差分进化算法用于模糊模型优化，能够使种群以较快的收敛速度、较好的搜索性能寻找全局最优个体，建立结构简单、精确度高的模糊模型．

1 预备知识

1．1 模糊分类系统

对于n 维m 类的分类问题，其中x = (x1，x2，…，xn)为输入变量，{g1，g2，…，gn}为输出类的标值号，则经典的模糊分类系统的规则可表示为［10］

Ri:if x1is μi1and x2is μi2and … and xnis μin，

then the pattern (x1，…，xn)belongs to gi． (1)其中，μi1，…，μin为模糊集合．其高斯型隶属函数为

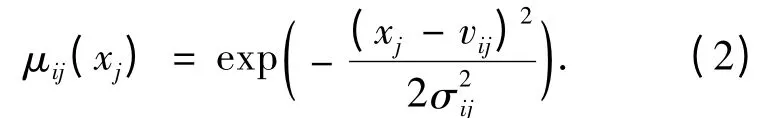
式中:νij，σij分别表示函数的中心和方差． 对于样本xk，模糊系统所对应的输出类别为激励强度最大的规则的后件类别号．

1．2 烟花算法

烟花算法是Tan 通过模拟烟花的爆炸过程而提出的一种群体智能算法［8］． 该算法在每一代都选择出性能较好的烟花作为父代，来产生子代火花用以搜索最优解．对于烟花xi，产生子代火花的数量si以及爆炸的范围Ai分别定义如下:

式中:si和A^是控制参数;L 为种群大小;fmax和fmin分别表示目标函数的最大值和最小值;ε 是一个极小的常量以避免除数为零．

为了避免性能优秀的烟花对子代的影响过大，以至于丧失种群多样性，需对si的大小范围进行限制:

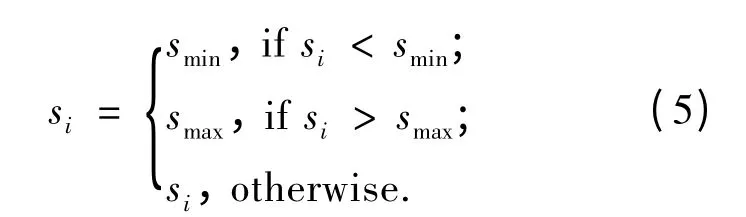
对于一个D 维的问题，随机选择烟花xi的z(z＜D)个位置，对每一个位置加上一个位移构成(1 ≤j ≤si，1 ≤k ≤z)．生成火花的方法有两种．大部分火花是通过对加上一个位移hk= Ai·rand(-1，1)而得到的，即

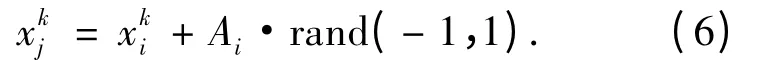
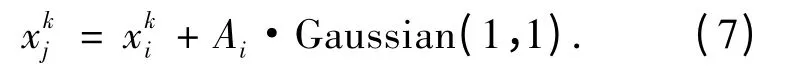
对于上述两种方法，如果产生的新的位置超出了搜索区间，需要将其映射到搜索区间内，方法如下:

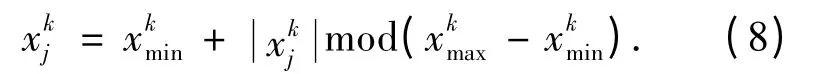
在每一次迭代中，所有的个体(包括烟花和火花)中的最优个体，总是被选为烟花进入下一代，并根据距离概率［9］选择其他L-1 个个体作为下一代的父体烟花．

1．3 差分进化算法

仅仅采用烟花算法对初始模糊模型进行优化，容易过早成熟收敛，陷入局部最优解［9］． 为了提高种群的多样性，扩大搜索范围，在每一次迭代过程中，采用烟花算法产生新的子代火花，并选择出较好的个体作为下一代烟花，然后执行差分算法对被选择出的烟花进一步优化． 差分算法的步骤为:

(1)变异操作．对于个体xi，在种群中随机选择3 个个体xr1，xr2和xr3，其中的一个个体加上另外两个个体的差值与权值系数的乘积，生成变异个体vi，即

vi= xr1+ γ(xr2- xr3)． (9)

式中:r1，r2，r3∈［1，L］;γ 是变异尺度因子，用来控制摄动幅度．

(2)交叉操作．在原始个体和变异个体之间进行比较，挑选出试验个体uji．采用二项式交叉，即

式中:cr是交叉概率;r(i)是(0，2 ×c ×n］之间的随机数．

(3)选择操作． 将原始个体和试验个体进行比较，比较优秀者被选择进入下一代种群．这个操作过程表示为

2 利用烟花算法和差分算法建立模糊分类系统

采用模糊C - 均值(FCM)聚类算法构造初始模糊系统，但初始模糊模型在分类精度以及可解释性方面的效果都比较差． 采用烟花算法和差分进化算法对模型的结构和参数进行学习和优化，并在进化算法中采用相似相融原理［10］对模型进行约简［11］，在保证系统精确度的前提下，简化系统结构，使得系统更好理解、透明性更高．

2．1 模糊分类系统的初始化

为了避免“维数灾”问题，首先进行特征变量的选择［11］，以降低系统的维度．并采用模糊C-均值(FCM)聚类算法辨识初始模糊模型［12］，其中初始聚类数为c，即初始的模糊模型规则数，取c = 3Nc(Nc为实际分类数)．

规则Ri的后件所对应的类标号值［11］为

其中，uik是数据xk对ith聚类中心的隶属度，且满足:

2．2 染色体编码

设定种群的个体数为L，染色体表示为Hp，p =1，2，…，L，第一条染色体根据初始模型的参数来构造，其中隶属函数的中心vij和方差σij为编码参数，则第一条染色体的编码为

H1= (v11，…，vcn，σ11，…，σcn)． (17)

搜索区域为［Hmin，Hmax］:

2．3 适应度函数

建立模型的主要目的是能够准确地模拟实际问题，为此，精确性是模糊分类系统的一个重要性能指标，可用分类误差来衡量模糊分类系统的精确性:

系统的解释性是指，人们容易通过该系统理解并学习实际问题的内部机理．一般情况下，模型的结构越复杂，所包含的模糊规则和模糊集合数量越多，人们学习该模型就越困难，模型的解释性就越差［11，13］． 若要使模型易于理解，应在满足精确性的前提下，采用尽可能少的规则和集合;而且，模糊规则必须满足一致性和完备性，输入变量的两个相邻的模糊集合应满足可区分性，并在恰当的隶属函数值处交叉．

精确性和解释性是模糊系统的两个重要指标，利用加权求和法的思想，将这两个指标综合，构成为如下适应度函数:

F = ω1JERR+ ω2NR+ ω3NS． (22)

式中:JERR为衡量模型精确性的指标，为类别被划分错误的样本数目;NR，NS分别为模糊规则和模糊集合的数目，用来度量模型的解释性;ω1，ω2和ω3为预先设置的权值参数，其值的大小一般是根据具体问题需要和经验进行选取．

2．4 模糊分类器的设计步骤

基于烟花算法和差分进化算法的模糊分类器设计的详细步骤如下．

步骤1:初始化．首先，对系统的特征变量进行选择，降低模糊系统的维度;其次，利用FCM 聚类算法构建初始模糊模型，并对初始种群P 进行染色体编码．

步骤2:计算模糊规则和模糊集合之间的相似度，并约简模糊模型结构．

步骤3:根据公式(3)、(5)计算每一个烟花所产生子代火花的数量，由公式(4)得出子代火花范围．

步骤4:根据公式(6)、(8)产生普通子代，根据公式(7)、(8)得到少量由高斯位移产生的子代．

步骤5:根据适应度函数值，选择最优个体，并在适应度排在前2L 的个体中随机选择L -1 个个体组成种群P'．选择概率为

步骤6:对由烟花算法得到的种群P'，采用差分算法，经过变异、交叉、选择操作得到种群P．

步骤7:判断是否满足步长终止条件，如果满足，返回步骤2;否则，算法执行结束．

2．5 算法流程图

模糊分类器设计步骤的算法流程如图1 所示．

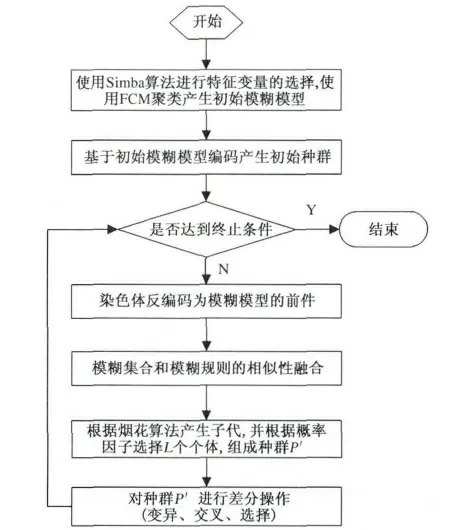
图1 模糊分类器设计算法流程图Fig．1 Flowchart of the fuzzy classifier generation

3 试验与分析

采用Iris 数据样本作为实验数据．Iris 数据是由4 维数据［x1:Sepal length;x2:Sepal width;x3:Petal length;x4:Petal width］的150 个样本组成．对实验数据的特征进行筛选，选择x3和x4为输入变量［3］;采用FCM 聚类对数据进行预处理，构建一个由9 个模糊规则和18 个模糊集合所组成的初始模型．该模型的结构复杂，且错误分类样本数目为10，分类精确度为93．3%，分类效果差．

采用烟花算法和差分进化算法对模型的结构和参数进行优化，并利用相似度原理对规则和集合进行约简．关于实验中一些常量参数的设定，笔者是在参考相关文献资料的基础上经过反复试验而获取的．选取不同的常量参数所得到的模糊模型，其性能有一定的差别． 经过多次实验和分析后，最终设定种群的大小L=40，进化代数为100，模糊集合和规则的相似性融合的阈值分别为0．4和0． 9，适应度函数参数ω1= 1，ω2= 0． 5，ω3=0．2．

经过优化后的模型精确性提高了很多，错误划分样本数目降为4，精确性度高达97．3%，模糊集合数减少到5，其隶属函数如图2 所示，模糊规则数降为3，模型的结构简单了许多，解释性得到了提高．

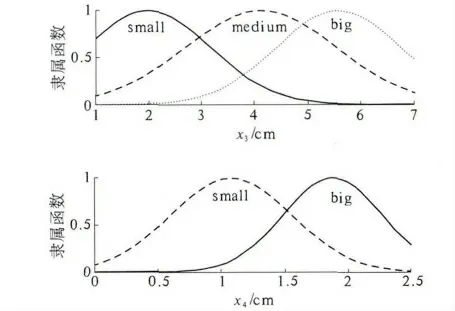
图2 优化后模糊模型的隶属函数图Fig．2 Membership function of the optimized fuzzy model

表1 列举了本文方法与其他文献方法的对比结果．可以看出，基于烟花算法和差分进化算法所建立的模糊分类系统分类精度高、结构简单、易于理解．文献［14 -15］中的分类系统的分类效果虽然比本文方法的精确度稍好一些，但系统所包含的模糊集合数目较多、结构复杂、解释性差．文献［16］中的分类系统与本文所建立的系统相比，结构更为简单，解释性稍好，但其分类准确度较差．总体来说，笔者所建立的模糊分类系统在精确性与解释性这两个相互矛盾的方面获得了较好的折衷，模型更为合理．

表1 Iris 分类问题不同建模方法的性能比较Tab.1 Comparison of different modeling methods on the Iris classification problem

4 结论

为了建立能够准确模拟实际问题并且易于被人们所理解的模糊模型，采用烟花算法和差分进化算法来建立模糊模型是一种很好的选择． 这是首次将烟花算法应用到模糊建模领域，利用烟花算法和差分算法对模型结构和参数进行优化． 在烟花算法中，性能较好的烟花在较小的范围内产生较多的子代个体，加快了收敛速度;另一方面，性能较差的个体在较大的范围内产生较少的子代个体，从而增大了搜索范围．而采用差分算法对子代火花进一步优化，能够提高种群的多样性，很好地解决了烟花算法容易过早地陷入局部最优的问题，并最终以较少的模糊规则和模糊集合数取得了精确性良好的模糊分类系统．

笔者采用的是加权求和法的方法构建适应度函数，将多目标转化为一个目标函数．但是，目前还没有确定某种算法能较好地确定权值大小，在这里仅是根据经验来设定权值大小，可见，这种方法具有一定的局限性．下一步，笔者将尝试并研究采用Pareto 最优解的理论来处理多个目标的问题．

［1］ 生龙，张洪斌． 二型模糊系统在音频信号分类中的应用［J］． 电子科技大学学报，2013，42(3):436 -441．

［2］ 郭亦文，李军，耿林霄． 基于遗传算法获取模糊规则［J］． 计算机应用，2014，34(10):2899 -2903．

［3］ 张永，吴晓蓓，向峥嵘，等． 基于决策树和遗传算法的模糊分类系统设计［J］． 东南大学学报(自然科学版)，2006，36(1):23 -36．

［4］ 冯冬青，张希平． 基于神经网络的自学习模糊控制［J］． 郑州大学学报(工学版)，2003，24(4):6-10．

［5］ 张景元． 基于神经网络的自适应模糊控制系统［J］． 计算机工程与设计，2014，35(10):3613-3616．

［6］ 王杰，周贺松． 增一型分层模糊系统结构的PCA优化方法［J］． 郑州大学学报(理学版)，2013，45(2):59 -63．

［7］ 张涛，洪文学． 基于模糊度的计算几何分类器权重分配［J］．控制与决策，2013，28(4):569 -573．

［8］ ZHENG Shaoqiu，JANECEK A，TAN Ying． Enhanced fireworks algorithm［C］//2013 IEEE Congress on Evolutionary Computation． Cancun，México:IEEE Press，2013:2069 -2077．

［9］ ZHENG Yujun，XU Xinli，LING Haifeng，et al． A hybrid fireworks optimization method with differential evolution operators［J］． Neurocomputing，2012，148:75 -82．

［10］SETNES M，BABUSKA R，KAYMAK U，et al． Similarity measures in fuzzy rule base simplification［J］．IEEE Transactions on Systems，Man and Cybernetics，1998，28(3):376 -386．

［11］张永，吴晓蓓，向峥嵘，等． 基于多目标进化算法的高维模糊分类系统的设计［J］． 系统仿真学报，2007，19(1):210 -215．

［12］文传军，汪庆淼，詹永照． 均衡模糊C 均值聚类算法［J］． 计算机科学，2014，41(8):250 -253．

［13］WANG Hanli，KWONG S，JIN Yaochu，et al． Multi-objective hierarchical genetic algorithm for interpretable fuzzy rule-based knowledge extraction［J］． Fuzzy Sets and Systems，2005，149(1):149 -186．

［14］ISHIBUCHI H，NAKASHIMA T，MURATA T． Threeobjective genetics-based machine learning for linguistic rule extraction［J］． Information Sciences，2001，136(1):109 -133．

［15］WANG J S，LEE C S G． Self adaptive neuro-fuzzy inference systems for classification applications［J］．IEEE Transactions on Fuzzy System，2002，10(6):790 -802．

［16］ZHANG Yong，WU Xiaobei，XING Zongyi，et al． On generating interpretable and precise fuzzy systems based on Pareto multi-objective cooperative coevolutionary algorithm［J］． Applied Soft Computing，2011，11(1):1284 -1294．