基于问题驱动的高等数学教学模式设计

朱全英，王志平

(大连海事大学，辽宁 大连 116026)

基于问题驱动的高等数学教学模式设计

朱全英，王志平

(大连海事大学，辽宁 大连 116026)

讨论基于问题驱动的高等数学教学方法及针对不同教学内容进行问题设计的实践教学模式，从启发性问题驱动、桥梁作用的问题驱动、多角度的问题驱动、直观性的问题驱动和实践性的问题驱动等方面探讨相关教学模式。

问题驱动；高等数学；问题设计；教学模式

一、引言

数学是培养学生创新能力和解决问题能力的关键学科。以建构主义理论为基础和问题驱动式教学打破了传统的“满堂灌”的课堂模式，以问题为导向，引导学生参与解决问题，在问题情境中建构知识。[1-2]在高等数学教学中引进问题驱动式教学模式，有利于激发学习兴趣，培养发现和解决问题的能力，增强实践能力和创新能力。

问题驱动式教学模式在高等数学教学中的应用，学界从方法的适用性和问题设计思想[3]等理论以及问题设计策略[4]方法等不同角度进行了探讨。问题驱动式教学模式的核心是问题的设计，设计出合理的、有意义的以及学生感兴趣的问题是问题驱动式教学中的重要任务。Barrows和Kelson认为，问题导向学习必须设计出能令人信服的问题真实情境，能引发多元的假设，并规划出符合课程目标的知识概念与技巧，以锻炼学习者的问题解决能力及创造性思维，同时，教学内容能整合、包含一个以上的学科。[2]可见，在问题驱动式教学中，好的问题设计是教学成功的基石。本文着重讨论好的问题设计应该具备的条件。

二、基于问题驱动的高等数学教学模式设计

针对不同的教学内容、不同的教学目的对问题的设计应该有不同要求，如有些问题要具有启发性，有些问题要具有搭建新旧知识的桥梁作用，提问题的角度要具有多样性，有些问题要具有直观性，有些问题要具有实用性等。

1.启发性问题驱动

建构主义理论认为，知识不是通过老师教给学生的，而是在一定的情境(社会文化)中，利用必要的学习资料(包括实践活动)，借助外界(老师、学习伙伴或其他相关人)帮助而进行的有意义的建构过程。以“问题”为引导，学生为了解决现实情境中的问题需要自己查阅资料、分工协作、知识分享来解决问题，并在解决问题的过程中不断总结、反思，通过查阅大量资料，从中抽取信息、组建信息，最终建构出属于自己的知识[2]。知识只有通过个体的主动建构，使其变成认知结构中的知识，它才能获得意义。

教师为了充分激发学生的主动性、积极性和质疑精神，启发学生自主建构认知结构，在学习一些数学概念时提出具有启发性的问题情境显得尤为重要。数学概念是对自然界中蕴含的规律和关系的高度抽象，因为其抽象性所以学生接受起来难度很大。但是每一个数学概念又都是有渊源的，往往是解决某些或某一类问题而产生的。因此通过追本溯源，可以把与概念相关的背景问题提出来以启发学生，引导学生自己去发现和概括这一概念，实现知识的建构。如学习“导数”概念时，可以提出以下具有启发性的引例。

引例：棒球大联赛票价的增长率问题。

美国的棒球大联赛吸引了大量的观众，而大联赛的票价也随之节节攀升，假设票价的变化趋势符合函数p(x)=9.41-0.19x+0.09x2,其中x是1990年以后的年数，p是票价，那么在x时刻，票价p的增长率是多少？

分析：从所给的函数表达式可知，用之前所学知识不能求出任一时刻票价的增长率，但是可以求出一段时间内票价的平均增长率，即当时间由x改变到x+Δx时，票价p在Δx这段时间内增长了Δp=p(x+Δx)-p(x)，则在Δx这段时间内票价的平均增长率为

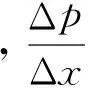
通过这种问题启发把概念的本质揭露出来，在引导学生解决问题的过程中阐明隐藏在问题背后的原理、脉络、思想和方法，尽可能地呈现或部分呈现、还原数学研究的过程。在这些问题情境下，教师转变为学习的辅导者，解答学生在解决问题过程中的思考和疑问，帮助学生肯定正确的思想和方法，否定错误的思路方法，实现有关该知识点的第一次知识体系构建。学生通过参与问题的解决过程，加强对相关概念的理解，这种理解不仅包含直观形象的认知，而且通过思考和比较，从理性层面也加深了对知识理论与方法的理解。

2.桥梁作用的问题驱动

建构主义理论指出，学习总是与一定的社会文化背景即“情境”相联系的，在实际情境下进行学习，可以使学习者能利用自己原有认知结构中的有关经验去同化和索引当前学习到的新知识，从而赋予新知识以某种意义。[3]学习者通过问题的解决建构新知识时，需要不断激活原有的知识经验，对当前问题做出分析和判断，对新、旧知识的合理性在问题解决过程中不断得到检验。因此，教师应该根据学生所掌握的知识和新知识的联系设置问题，为学生搭建知识框架，引导学生构建新知识，从而能够使学生实现由现有认知水平向潜在认知水平的发展。如“微分”概念的教学，如果直接给出定义，学生会觉得很难理解和接受。这时候需要教师提供一些起桥梁作用的问题帮助学生搭建知识框架，构建一系列的知识体系。

问题1：函数y=x2，当x由2变化到2+0.01时，函数的增量是怎样的？

问题2：增量的主要部分是什么？函数y=x2在x=2处的导数与增量有什么关系？

问题3：对于函数y=x3和y=2x同样的问题如何解决？

通过这些问题引导学生发现微分与增量的关系、微分和导数的关系，进一步了解定义微分的意义：微分是用来近似增量的，而且求微分比求增量简单。在学生解决这些问题的过程中，教师的作用主要是“布阵设疑，搭桥铺路”。不是急于给出答案，而是通过旁敲侧击、点拨诱导，使学生恍然大悟，让思维的火花从学生的脑海里迸发出来，这对激发学生的悟性和创造性思维极为有利。[4]

3.多角度的问题驱动

数学理论的学习只有经历了从不同的角度、不同侧面反复印证的曲折的过程后才能“吃透”理论的本质特征。顾泠沅先生认为，“在教学中用不同形式的直观材料或事例说明事物的本质属性，或变换同类事物的非本质特征以突出事物的本质特征。目的在于使学生理解哪些是事物的本质特征，哪些是事物的非本质特征，从而对这一事物形成科学概念”。[5]因此，在教学中围绕同一概念可以从不同角度和侧面提问题，帮助学生正确理解数学理论的本质特征。

比如，“罗尔定理”的教学中，学生通过证明过程只能承认定理的正确性，并不一定能抓住定理的本质特征，因此，教师可以从不同角度提出问题，帮助学生真正理解其本质。在实际中往往否定条件提出问题：

问题1. “如果函数在闭区间上不连续，结论能不能成立？”举出反例。

问题2. “如果函数在开区间内不可导，结论能不能成立？”举出反例。

问题3. “如果两端点的函数值不相等，结论是怎样的？”

学生通过自己的观察、思考和判断，能够深刻理解这一定理的实质，进一步得到微分中值定理的结论，就像他们自己发现了定理一样，这无疑将会增强他们的创新意识。

4. 直观性的问题驱动

美国数学家斯蒂恩指出：如果一个特定的问题可以被转化为一个图形，那么思想就整体地把握了问题，并且能创造性地思索问题的解法。教师在教学中尽力做到把问题形象化、直观化，用图形来描述问题，从而起到事半功倍的效果。

比如在定义凹弧和凸弧时，直接给出不等式形式的定义，学生难以接受。教师可以通过图形刻画出凹凸弧的特点，以问题为驱动，给学生一个形象的解释，学生易于理解和接受。

问题：从图形上看，凸弧上的弦在弧的下面，怎样比较弧的高度和弦的高度？

弧高大于弦高就表示了凸弧，弧高小于弦高就是凹弧。再给出不等式的定义就水到渠成了。

再比如“数项级数的和”总是令人“难以置信”，直观化的问题驱动可以帮助学生更好地理解这一数学概念。

这个例子就把看似难以捉摸的概念具体化形象化了。这无疑会激发学生的学习兴趣，更进一步激发学生的创造性。

通过这一问题的解决，学生从直观上得出了此极限的值，后面的推理证明就顺理成章，学生容易接受而且不易忘记。

5.实践性问题驱动

学生学习高等数学的目的不是单一的为专业课打基础，而是要培养分析问题、解决问题的能力，学会运用数学知识和方法解决各种实际问题。训练学生解决一些实际问题，不仅锻炼学生解决问题的能力，而且会激发学习兴趣，同时巩固所学知识，为进一步的学习打下坚实的基础。

教师结合不同专业学生的专业特点选择适当的案例，指导学生建立数学模型并求解。

比如，市场营销专业的学生可以解决这样的案例：小王手里有200元钱，他需要购买两种商品：光盘和录音带。假设购买x张光盘和y盒录音带的效用函数为U=U(x，y)=lnx+lny，设每张光盘8元，每盒录音带10元，问如何分配这200元钱，才能达到最满意的效果。

这个案例的解决用到多元函数微分法的应用、条件极值的求法等内容。通过这一案例的解决，学生会发现高等数学并不只是抽象的定理和符号，而是跟日常生活息息相关，因此学习高数的积极性就会大大提高。当然很多案例是具有普遍性的，对任何专业的学生都适用。

把数学实践融入问题驱动式教学，并将一些典型应用问题引入教学内容，促进数学教学与现代科技的结合；数学实践贯穿了数学建模的思想方法，以实际问题为各教学案例，能够提高学生应用数学解决实际问题的能力。

三、结语

本文针对不同教学内容进行了不同特点的问题设计，从启发性问题驱动、桥梁作用的问题驱动、多角度的问题驱动、直观性的问题驱动和实践性的问题驱动等几个方面来探讨在高等数学教学中问题驱动式的教学模式设计。在实际的高等数学教学实践中，怎样灵活应用不同特点的问题驱动以及如何有效地发挥问题驱动式教学的优点等方面都需要进一步研究并实践。

[1] 曹辉.建构主义课程理论的“情境”解说[J].内蒙古师范大学学报,2015(12)：6-8.

[2] 吴刚.基于问题式学习模式(PBL)的评述[J].陕西教育,2014(4)：3-7.

[3] 滕吉红.问题驱动式教学模式在高等数学教学中的探索[J].高等教育研究学报，2012(12)：89-90.

[4] 黄贵.关于问题驱动数学教学的几种策略[J].基础教学研究, 2008(3)：90-91.

[5] 顾泠沅.华人如何学习数学[M].南京：江苏教育出版社，2005：247-273.

2014-07-01

辽宁省高等学校教学改革项目“基于问题驱动的高等数学教学方法创新研究与实践”

朱全英(1969-)，女，讲师，主要从事应用数学研究。

G642.0 < class="emphasis_bold">文献标识码：A

A

1006-8724(2015)01-00084-03