台阶型类石墨烯纳米系统中的线性交流输运

叶恩钾,王继成,韩 愈,王利光

(江南大学 理学院,江苏 无锡 214122)

台阶型类石墨烯纳米系统中的线性交流输运

叶恩钾,王继成,韩 愈,王利光*

(江南大学 理学院,江苏 无锡 214122)

利用紧束缚近似模型、格林函数方法和交流输运理论，研究两类台阶型石墨烯纳米系统中的电子交流输运性质。研究表明，台阶型石墨烯纳米系统中的界面散射导致直流电导变小。在费米能附近，第I类台阶型石墨烯纳米系统对外加电压作电容响应，第II类台阶型石墨烯纳米系统的半导体性质取决于窄端引线的导电性质。局域电子态密度的分布表明，狄拉克点电子局域在其中一类子晶格上无法传导，电导被抑制。当通道打开，电子态密度在两类子晶格上分布较均匀，利于电子传导。

电子输运；格林函数方法；石墨烯；紧束缚近似

0 引 言

由于良好的力学性质和电子高迁移率，单层二维碳原子薄膜材料石墨烯(graphene)的研究受到了人们极大的关注。石墨烯中电子在费米面附近的行为类似于狄拉克(Dirac)电子，从而使其表现出诸多不同寻常的量子效应，如克莱因佯谬，反常量子霍尔效应和谷电子极化等[1-4]。通过对石墨烯材料的剪裁，可得到两种不同边缘结构的石墨烯纳米条带(graphene nanoribbon)：锯齿型(zigzag)和扶手椅型(armchair)。其中，锯齿型石墨烯纳米条带(zGNR)表现为金属电导性，扶手椅型石墨烯纳米条带(aGNR)的导电性取决于其宽度Na。当宽度满足Na=3n+2时，扶手椅型石墨烯纳米条带为金属性，其它情况为半导体性[5-8]。两种不同边缘类型的石墨烯纳米条带可作为基本结构拼接成各种不同几何形状的异质结和功能性电子器件，如石墨烯透射结、场效应管等[9-12]。然而，上述研究主要集中在各种结构中的直流电导输运，而交流输运的性质研究对于石墨烯电路的电子传导具有重要影响和实际应用价值[13-17]。

本文应用递归格林函数方法和Büttiker交流输运理论，研究由宽窄不同的扶手椅型石墨烯纳米条带拼接而成的台阶型石墨烯纳米系统中的线性交流输运性质。详细介绍了递归消除法(recursive decimation method)处理台阶型石墨烯纳米开放系统的电子输运问题。考虑不同宽度扶手椅型石墨烯纳米条带中的金属性和半导体性，通过比较两种宽度的台阶型石墨烯纳米系统，重点讨论在费米能附近和第二通道打开条件下的动态电导(dynamic conductance)性质。此外，还讨论了局域电子态密度(local density of states)的分布对于电子传导性质的影响。

1 模型和理论

1.1 哈密顿量模型

台阶型石墨烯纳米器件为开放系统，由两条半无限长、不同宽度的扶手椅型石墨烯纳米条带连接而成，且上下对称，见图1。采用最近邻紧束缚近似模型，系统的哈密顿量为：

(1)

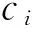
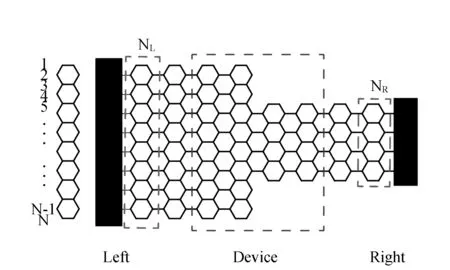
图1 台阶型石墨烯纳米系统晶格模型(纳米系统的左右引线宽度分别为NL和NR)Fig.1 Schematic structure of step-shaped graphene nano-system with the widths of left and right leads NL and NR respectively

为了便于开放系统的数值运算，将模型分为3部分：左(L)引线，右(R)引线和中心器件(D)部分。中心器件用蓝色虚线框标注。左右两条半无限长引线的单位晶胞与中心器件两端宽度一致，分别为NL和NR，如图中红色虚线框和左侧单位晶胞图所示。左右引线在无限远处与电子库相连接，图中用黑色电极等效表示。由此，系统哈密顿量可表示为：

(2)

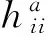
(3)

1.2 递归格林函数方法和局域部分态密度

定义系统的格林函数：(E-H)g(E)=I，根据对系统的分区，格林函数矩阵同样可分为3部分，即：

(4)

中心器件格林函数可写为：

(5)

其中∑L(R)(E)=HD L(R)gL(R)(E)cc为左(右)引线的自能，gL(R)(E)=(E-HL(R))-1为左(右)引线的格林函数。由于系统是开放的，gL(R)(HL(R)D)矩阵为无限大，无法进行数值计算。这里采用递归消除法(recursive decimation method)[18-19]，对半无限长的引线进行重整化，从而得到有限矩阵大小引线的有效哈密顿量，即自能。

如图2所示，任选引线中相邻的3列晶胞，其哈密顿量分别为h11，h22和h33。取第2列晶胞，将它消除。考虑晶胞2与相邻晶胞之间的相互作用v12/v32，第2列晶胞消除之后，晶胞1和3的有效哈密顿量为：

(6)

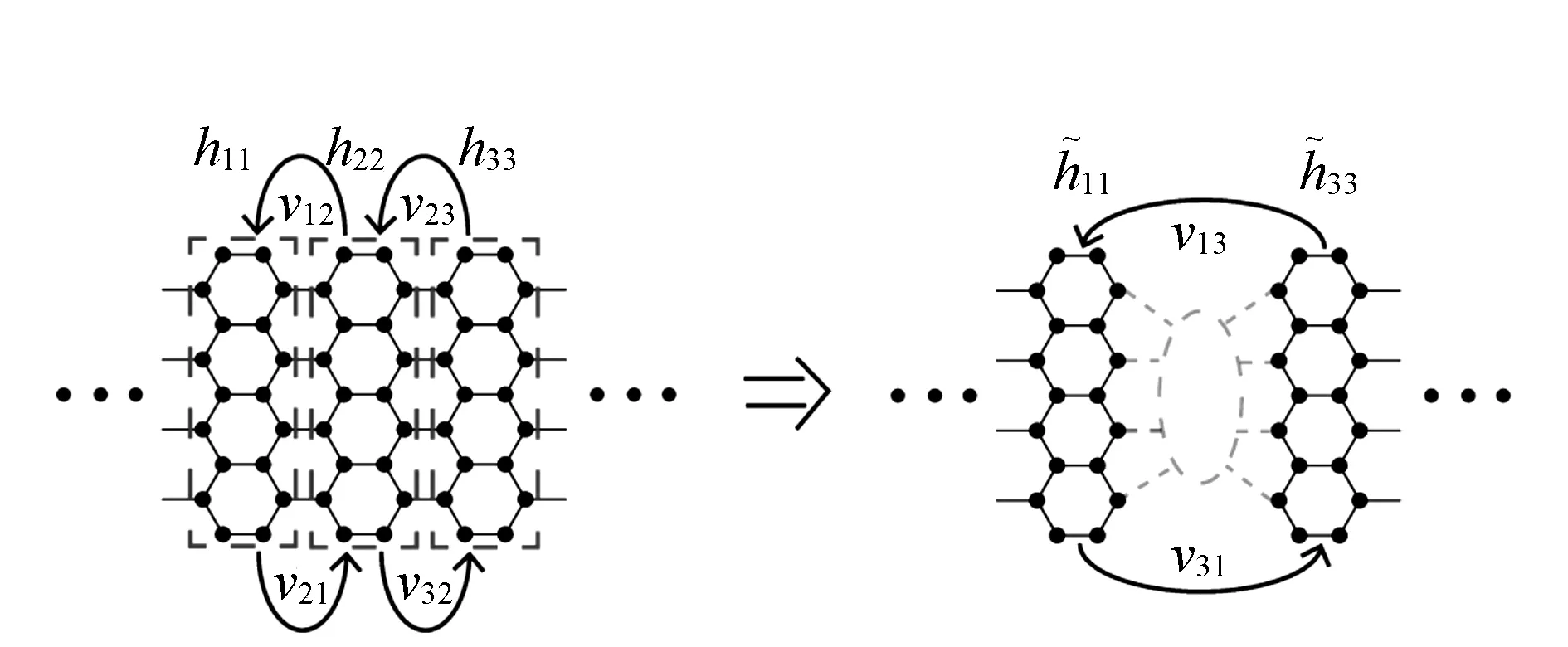
图2 石墨烯纳米条带引线中的递归消除法Fig.2 Procedure of recursive decimation method of aGNR lead.

对于半无限长的引线，将大批量地消除取样晶胞，并采用递归方法。令引线晶胞数量为N，每一次消除之后，总的晶胞数量变为N/(2n)，n为消除的次数。晶胞2消除之后，晶胞1和3之间的间接耦合相互作用变为：

(7)

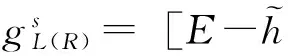
(8)

1.3 交流输运理论

本文采用Büttiker交流输运理论，计算台阶型石墨烯纳米系统中的动态电导(dynamicconductance)，也叫做导纳(admittance)。考虑频率的一阶近似，动态电导为[21-22]：

(9)

式中ω为外加电压频率；α(β)标记不同端口的引线；Gα β(0)为直流电导；Eα β为emittance，是Büttiker交流输运理论中对于电纳的量子描述。这里直流电导与传导系数Tα β相关[20]，

(10)

式中h为普朗克常数;e为电子电荷量。根据交流输运理论，emittance为

(11)

它描述裸电荷(第一项)与感应电荷(第二项)对于外界电压微扰的交流响应。裸电荷和感应电荷的交流相应分别对应类似电感(inductive-like)性质和电容(capacitive)性质并相互竞争。其中dn(α,r,β)/dE为局域部分态密度(local partial density of states，LPDOS)，可用格林函数表示[23]：

(12)

在交流输运理论中，局域部分态密度表示从β端口入射的载流子，经过位置r，最终到达端口α的散射过程。由此，将入射端口或者出射端口求和，可以得到注入率(injectivity)或者放射率(emissivity)，分别为：

(13)

将所有端口相加，即得到常用的局域态密度(local density of states，LDOS)：

(14)

u(r)为纳米器件系统的特征势，描述散射过程中电子感应的电势，它满足泊松方程[21]：

(15)

这里采用Thomas-Fermi屏蔽模型：Π(r,r′)=δ(r-r')dn(r)/dE和准中性近似：▽2uβ(r)=0以简化数值计算，由此可得特征势为[21,24]

(16)

由上述公式得动态电导满足：∑αGα β(ω)=

∑βGα β(ω)=0，因此系统满足流守恒和规范不变性。

2 结果和讨论

首先比较台阶型石墨烯纳米系统和均匀扶手椅型石墨烯纳米条带的直流电导(dcconductance)、态密度(DOS)和交流部分(emittance)的性质。如图3(a)和(b)所示，描述两金属性扶手椅型石墨烯纳米引线拼接成的台阶型纳米系统(I类)，其左右引线宽度分别为(a)(NL,NR)=(23,

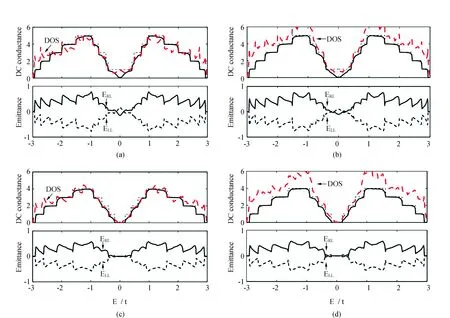
图3 直流电导(单位：2e2/h)，态密度DOS和交流量子电纳随着能量E的演化行为(I类台阶型石墨烯纳米系统的左右引线宽度为(a)(NL,NR)=(23,11)，(b)(NL,NR)=(35,11)；II类台阶型石墨烯纳米系统的左右引线宽度为(c)(NL,NR)=(21,9)，(d)(NL,NR)=(33,9)。黑色阶梯形虚线为右引线石墨烯纳米条带的直流电导图)Fig.3 The dc conductance(in the unit of 2e2/h), DOS and emittance as a function of electron energy in step-shaped graphene nano-systems with the sizes of type I: (a) (NL,NR)=(23,11), (b) (NL,NR)=(35,11) and type II: (c)(NL,NR)=(21,9),(d)(NL,NR)=(33,9) respectively. The black dashed stepped lines in the up panels are the dc conductances of right aGNR lead

11)和(b)(NL,NR)=(35,11)。图3(c)和(d)描述两半导体性扶手椅型石墨烯纳米引线拼接成的台阶型纳米系统(II类)，其左右引线宽度分别为(c)(NL,NR)=(21,9)和(d)(NL,NR)=(33,9)。由图3可知，在整个传导能量范围里，台阶型扶手椅型石墨烯纳米系统的直流电导(黑色实线)相比均匀扶手椅型石墨烯纳米条带的直流电导(黑色虚线)总体变小，这是由于不同宽度引线间界面散射的结果。交流部分(emittance)的变化跟随直流电导变化。然而，由于引线宽度和比例尺寸不同，导致费米面(狄拉克点，Diracpoint)附近输运性质完全不同。图3(a)中，I类台阶型石墨烯纳米系统在费米面附近发生反共振效应，直流电导变小。交流部分ERL<0，表示系统中裸电荷响应贡献小于感应电荷响应，此时系统呈电容性质。随着左端引线宽度变大[图3(b)]，界面散射加剧，费米面附近的电导进一步变小，而此时系统仍旧呈现电容性。而由于宽引线提供更多的电子通道模式，电子态密度(DOS)总体增大。图3(c)和图3(d)中，II类台阶型石墨烯纳米系统在费米面附近的电导为零，系统存在能隙，呈现半导体性质。由于交流部分ERL=0，系统在费米面附近的裸电荷响应和感应电荷响应贡献均等，系统没有交流响应。同样，由于宽引线提供额外的电子通道模式，电子态密度(DOS)总体增大。

为了进一步描述系统的反共振效应和半导体性质，笔者重点讨论尺寸为(NL,NR)=(23,11)的I类台阶型石墨烯纳米系统和尺寸为(NL,NR)=(21,9)的II类台阶型石墨烯纳米系统在狄拉克点附近和第二通道打开处的输运性质，见图4和图5。图中，分别标记狄拉克点为A/A′和C/C′，标记第二通道打开处能量为B/B′和D/D′。在图4中，系统的左右引线表现为金属性，电子能带的第一传输通道打开，见图4(a)底部能带图。因此拼接后的台阶型系统在狄拉克点处电子态密度(DOS)增大，见红色虚线。然而，此处参与传输的狄拉克电子干涉相消，发生反共振效应，电导为零。同时，反共振效应导致裸电荷的交流响应贡献减少(ERL<0)，狄拉克点处系统表现为电容性。而当第二通道打开时，直流电导开始迅速增大，裸电荷响应占主导(ERL>0)，系统呈类似电容性，见图4中B/B′点和对应的能带通道。狄拉克点C附近的直流电导为零，系统表现为半导体性质(图5)。图中零电导范围与右引线电子能带的带隙吻合，因此系统的半导体性质取决于引线的能带性质，引线能带图见图5(a)。由于狄拉克点处于能隙之中，电子态密度为零，系统没有裸电荷和感应电荷，不存在交流响应(ERL=0)。当电子能带中第二通道打开时，情况与图4类似，直流电导增大，系统表现为类似电感性质。

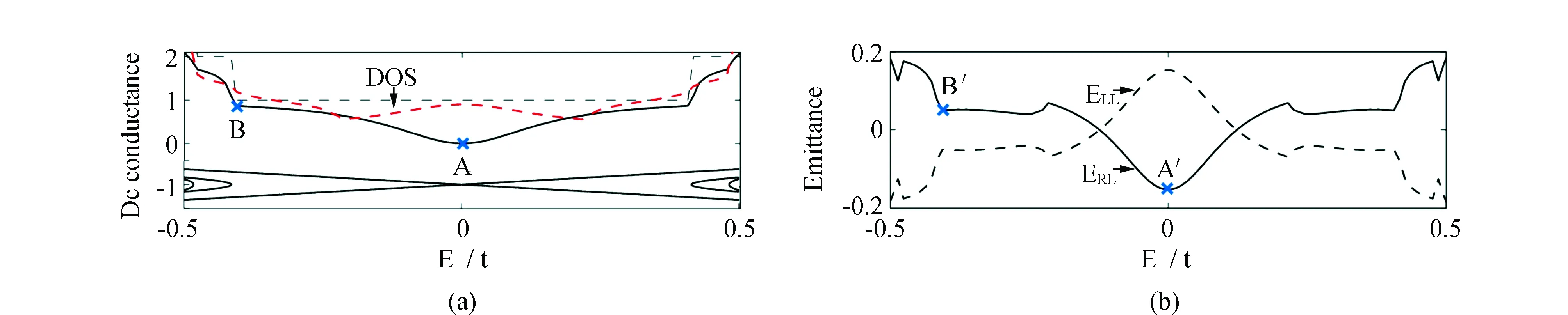
图4 台阶型石墨烯纳米系统(NL,NR)=(23,11)在低能量区域动态电导演化图(A(A′)和B(B′)分别为狄拉克点和导通能量点)Fig.4 The evolution of dynamic conductance of step-shaped graphene nano-systems with the size of (NL,NR)=(23,11) at low energy regime(A(A′) and B(B′) represent the Dirac point and conducting point)

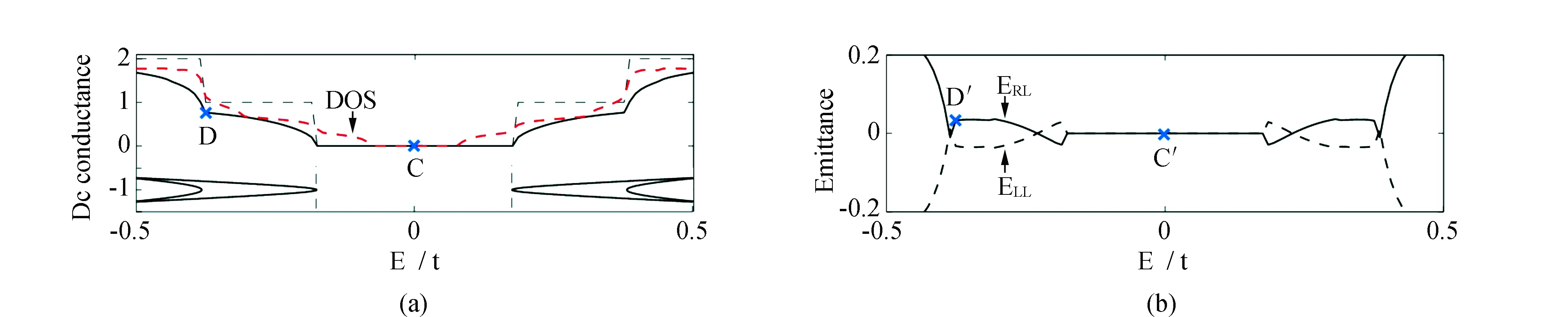
图5 台阶型石墨烯纳米系统(NL,NR)=(21,9)在低能量区域动态电导演化图(C(C′)和D(D′)分别为狄拉克点和导通能量点)Fig.5 Evolution of dynamic conductance of step-shaped graphene nano-systems with the size of (NL,NR)=(21,9) at low energy regime(C(C′) and D(D′) represent the Dirac point and conducting point)

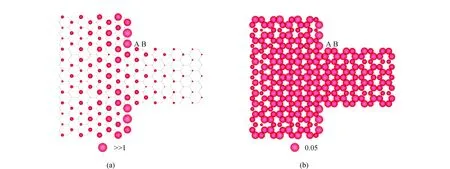
图6 台阶型石墨烯纳米系统(NL,NR)=(23,11)的局域态密度分布图Fig.6 Distribution of local density of states of step-shaped graphene nano-systems with the size of (NL,NR)=(23,11)

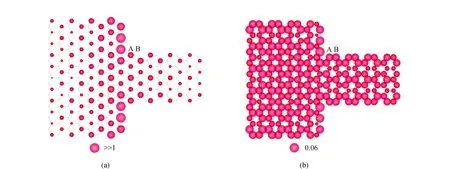
图7 台阶型石墨烯纳米系统(NL,NR)=(21,9)的局域态密度分布图Fig.7 Distribution of local density of states of step-shaped graphene nano-systems with the size of (NL,NR)=(21,9)

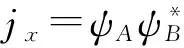
3 结 论

研究了分别由金属性和半导体性扶手椅型石墨烯纳米条带拼接而成的两类台阶型石墨烯纳米系统的电子动态电导输运性质。重点讨论了费米面(狄拉克点)和第二通道打开处的直流电导、交流响应和局域态密度分布性质。结果表明，I类台阶型石墨烯纳米系统存在反共振效应，抑制直流电导输运并具有电容性；II类台阶型石墨烯纳米系统的半导体性质由窄端引线的半导体性质决定，在能隙中不存在交流响应。当第二通道打开时，两类台阶型石墨烯纳米系统的电导增大，并表现出类似电感性质。

[1]Novoselov K S, Geim A K, Morozov S V, et al. Electric field effect in atomically thin carbon films [J]. Science, 2004, 306:666-669.

[2]Zhang Y, Tan Y, Stormer H L, et al. Experimental observation of the quantum Hall effect and Berry’s phase in graphene [J]. Nature, 2005, 438:201-204.

[3]Neto A H C, Guinea F, Peres N M R, et al. The electronic properties of graphene [J]. Rev. Mod. Phys., 2009, 81(1): 109-162.

[4]Novoselov K S, Fal V I, Colombo L, et al. A roadmap for graphene [J]. Nature, 2012, 490(7 419): 192-200.[5]Wakabayashi K, Fujita M, Ajiki H, et al. Electronic and magnetic properties of nanographite ribbons [J]. Phys. Rev. B, 1999, 59(12): 8 271-8 282.

[7]Peres N M R, Neto A H C, Guinea F. Conductance quantization in mesoscopic graphene [J]. Phys. Rev. B, 2006, 73(19): 195 411(1-8).

[8]Wakabayashi K, Takane Y, Yamamoto M, et al. Electronic transport properties of graphene nanoribbons [J]. New Journal of Physics, 2009, 11(9): 095016(1-20).

[9]Naumis G G, Terrones M, Terrones H, et al. Design of graphene electronic devices using nanoribbons of different widths [J]. Appl. Phys. Lett., 2009, 95(18): 182 104(1-3).

[10]Ye E, Sui W, Zhao X. Topological asymmetry induced electronic transport in three terminal graphene nano ribbon structure [J]. Appl. Phys. Lett., 2012, 100(19): 193 303(1-4).

[11]Peng S, Jin Z, Ma P, et al. The sheet resistance of graphene under contact and its effect on the derived specific contact resistivity [J]. Carbon, 2015, 82: 500-505.

[12]Kim Y D, Kim H, Cho Y, et al. Bright visible light emission from graphene [J]. Nature Nanotechnology, 2015,10:676-681.

[13]Roland C, Nardelli M B, Wang J, et al. Dynamic conductance of carbon nanotubes [J]. Phys. Rev. Lett., 2000, 84(13): 2 921-2 924.

[14]Zhang J, Yin Z, Zheng X, et al. Gauge-invariant and current-continuous microscopic ac quantum transport theory [J]. The European Physical Journal B, 2013, 86(10): 1-5.

[15]Ye E, Nie Y, Shi H, et al. Dynamic conductance in L-shaped graphene nanosystems [J]. J. Appl. Phys., 2015, 117(1): 014303(1-6).

[16]Zhang Ling,Zeng Yan,Zhou Ai,et al.The energy transmission characteristics of conical optical fiber[J].Journal of Natural Science of Heilongjiang University,2014,31(1):106-111.

[17]Hua Xuan,Zhou Ai,Wang Liguang.Study on optical bistabitity in a four-lever inverted Y-type atom system[J].Journal of Natural Science of Heilongjiang University,2014,31(4):540-545.

[18]Sols F, Macucci M, Ravaioli U, et al. On the possibility of transistor action based on quantum interfere ence phenomena [J]. Appl. Phys. Lett., 1989, 54(4): 350-352.

[19]Lan J, Ye E, Sui W, et al. Admittance of T-stub graphene nanoribbon structure [J]. PCCP, 2013, 15(2): 671-679.

[20]Datta S. Electronic Transport in Mesoscopic Systems [M]. Cambridge,England.Cambridge University Press, 1997.

[21]Büttiker M. Capacitance, admittance, and rectification properties of small conductors [J]. Journal of Physics: Condensed Matter, 1993, 5(50): 9 361-9 378.

[22]Büttiker M, Thomas H, Prêtre A. Current partition in multiprobe conductors in the presence of slowly oscillating external potentials [J]. Z. Phys. B: Condens. Matter, 1994, 94(1-2): 133-137.

[23]Gasparian V, Christen T, Büttiker M. Partial densities of states, scattering matrices, and Green’s functions [J]. Phys. Rev. A, 1996, 54(5): 4 022-4 031.

[24]Sheng W, Zheng Q, Wang J, et al. Dynamic and nonlinear magnetoconductance: Numerical analysis in two dimensions [J]. Phys. Rev. B, 1999, 59(1): 538-545.

Linear ac transport in step-shaped graphene system

YE En-Jia,WANG Ji-Cheng,HAN Yu,WANG Li-Guang*

(School of Science, Jiangnan University, Wuxi 214122,Jiangsu,China)

The properties of ac transport of step-shaped grpahene nano-system are investigated by employing the tight-binding approximation, Green’s function method and ac transport theory. The results show that the dc conductances are suppressed due to the interface scattering in the step-shaped graphene nano-system. The step-shaped graphene nano-system of type I responds capacitively to the external applied voltage. While the semiconducting feature of the step-shaped graphene nano-system of type II is determined by the narrow connected graphene lead. According to the results of distribution of LDOS, the conductance is suppressed due to the location of electrons only at one of the sublattices. However, the conductance increases as the channel opens and the uniform locations of electrons on both the two sublattice.

electronic transport; Green’s function method; graphene; tight binding approximation

10.13524/j.2095-008x.2015.04.065

2015-10-19

国家自然科学基金资助项目(11447206，11504137)；江苏省自然科学基金资助项目(BK20140131)

叶恩钾(1985-)，男，浙江永嘉人，讲师，博士，研究方向：介观纳米电子输运，E-mail：yeenjia@jiangnan.edu.cn;*通讯作者：王利光(1951-)，男，黑龙江绥化人，教授，博士研究生导师，研究方向：纳米电子学与理论物理，E-mail:wangliguang@jiangnan.edu.cn。

O488

A

2095-008X(2015)04-0055-07