基于数学实验的勾股定理教学实践<br/>——苏科版数学教材八上3.1勾股定理教学设计

基于数学实验的勾股定理教学实践
——苏科版数学教材八上3.1勾股定理教学设计

2015-03-17

中学数学杂志 2015年8期

关键词：勾股定理直角三角形正方形

基于数学实验的勾股定理教学实践
——苏科版数学教材八上3.1勾股定理教学设计

☉江苏省扬州大学附属中学东部分校万广磊

一、教材分析

1.本课的地位与作用

勾股定理是反映自然界规律的一条重要结论，它是初等几何中最精彩的，也是最著名和最有价值的定理之一，被誉为“几何明珠”，它在数学的发展历程中占有举足轻重的地位，在现实生活中也有广泛的应用.

本节课是《九年制义务教育课程标准实验教科书》（苏科版2013年版）八年级上册3.1“勾股定理”的第一课时，勾股定理的实质是从边的角度进一步对直角三角形的特征进行刻画.此前学生已经学习了三角形的有关知识，如三角形的三边不等关系、三角形内角和定理、三角形全等的性质与判定、直角三角形的斜边上中线性质、等腰三角形的性质与判定、轴对称图形等，初步感受到了公理化的思想.此外，在七年级下学期，学生也学过利用图形面积来探究数式运算规律的方法，如单项式乘多项式法则、多项式乘多项式法则、乘法公式、因式分解等知识和方法，初步感受了数形结合的思想.

本节课是在学生原有的认知水平基础上，进一步研究直角三角形的三边之间的二维等量关系.通过数学实验的系列开展，学生自主探索和发现勾股定理，构建知识链，数学活动经验和数学思维能力得到丰富和发展.此外，探求勾股定理的过程也蕴含了丰富的数学思想：把直角三角形“形”的特点转化为三边之间“数”的关系，体现了数形结合思想；用“割”、“补”的方法探究三个正方形面积的关系，体现了转化思想；从特殊直角三角形到一般直角三角形，从直角三角形到锐角三角形和钝角三角形，都体现了特殊到一般的思想和数学哲学的辩证思想.另外，从数学文化史的角度看，勾股定理的发现、验证也蕴含着文化价值和理性精神.

2.教学目标

（1）知识与技能：能利用实验探究验证勾股定理，理解勾股定理并会简单应用.

（2）过程与方法：通过系列化数学实验引导学生经历观察、思考、猜想、实验、验证、反思的全过程，发展合情推理、归纳和概括能力，体会数形结合、转化等数学思想.

（3）情感态度与价值观：培养学生独立思考、合作交流的意识，体验成功喜悦，了解勾股定理历史，感受其文化价值，增强民族自豪感，激发学习热情.

3.教学重点、难点

董林伟主任在《初中数学实验教学的理论与实践》一书中说：“数学实验不是学生被动地接受课本上的或老师叙述的现成结论，而是学生从自己的‘数学现实，出发，通过自己动手、动脑，用观察、模仿、实验、猜想等手段获得经验，逐步建构并发展自己的数学认知结构的活动过程”.［1］

结合以上关于数学实验的论述，特制定教学重点、难点如下：

（1）教学重点：通过数学实验发现和验证勾股定理，引导学生获得研究问题的方法经验，并简单应用勾股定理.

（2）教学难点：运用转化的思想，通过“割”、“补”的方法探索、验证勾股定理.

二、教法学法

孙朝仁所长指出：“数学实验课在教学设计时既要遵循目标性、整体性、多样性和简约性等原则，还要融入微观的经验元素、直观元素、普适元素及创造元素，方能释放数学实验的内在力量”.［2］

据此，教法设计和学法指导如下.

1.教法设计

采用探究发现式教学，通过系列数学实验，提供自主探究交流的空间，充分调动学生的学习积极性，有目的地探索和应用勾股定理.

2.学法指导

网格纸和拼图实验为学生设计计算面积的数学实验平台，结合多媒体课件演示，引导学生探索勾股定理.

3.教学准备

实验用的网格纸，课件（含几何画板文件）.

三、教学过程

1.创设情境，导入新课

图1

图2

图3

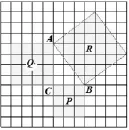
图4

（1）展示1955年希腊为纪念2500年前的毕达哥拉斯学派而发行的邮票，如图1所示.

思考：学生说出图中三角形的形状，指出三个正方形的面积之间的关系.

（2）展示2002年在北京召开的国际数学家大会的徽标，如图2所示，简单介绍会议背景.

思考：学生说出图中大正方形的面积计算方法.

设计意图：情境创设尊重了教材的编写意图，邮票和会徽的展示说明勾股定理所赢得的尊重，激发学习兴趣.初步感受勾股定理的文化价值，为下一步数学实验做铺垫.

2.实验探究，合作交流

实验一：画一画.

把直角三角形ABC纸片放在如图3所示的网格图中（每个小正方形边长为1 cm），分别以三边为边向外翻作正方形，观察并思考，再填空：

（1）正方形P的面积为________cm2，正方形Q的面积为________cm2，正方形R的面积为________cm2.

（2）你能发现图中正方形P、Q、R的面积之间有什么关系吗？从中你发现了什么？

说明：实验一以特殊的等腰直角三角形来铺垫定理的发现，计算面积过程相对简单.

实验二：想一想.

思考：其他一般直角三角形是否也有类似的性质呢？我们来继续观察图4.

（1）正方形P的面积为_______cm2，正方形Q的面积为________cm2，正方形R的面积为________cm2.

（2）你发现这个图和邮票中的图有什么关系吗？正方形P、Q、R的面积之间的关系是什么？

（3）你会用直角三角形的边长表示正方形P、Q、R的面积吗？

（4）你能发现直角三角形三边长度之间存在什么关系吗？与同伴进行交流.

说明：实验二通过发现图4和邮票中的图之间的关系是面积不变，因此学生在网格图中计算R的面积时有了目标，因此要通过“割”与“补”的方法将R转化为几个图形的和差，如图5、图6所示，切实加深对数形结合和转化思想的理解.

图5

图6

实验三：试一试.

（1）按照以下要求操作（请学生拿出实验用的网格纸进行操作）：

①在实验用的网格纸中，画出两条直角边分别为任意整数值的直角三角形，分别以三边为边向外翻作正方形.

②验证结论对直角三角形是否成立？

（2）学生用文字语言总结，并用几何语言表达自己的发现.

学生猜想（以回答出该问题的同学命名）：在直角三角形中，以斜边为边的正方形面积等于以两直角边为边的正方形面积之和（或直角三角形的两条直角边的平方和等于斜边的平方）.

说明：实验三从特殊的直角三角形到一般的直角三角形进行探究，揭示了勾股定理的普遍性，都可以从面积角度和代数式角度进行表述.

实验四：辨一辨.

（1）按照以下要求操作（让学生拿出实验用的网格纸进行操作）：

①在实验用的网格纸中，同桌的两人各自画出两条边分别为任意整数值的钝角三角形和锐角三角形，分别以三边为边向外翻作正方形.

②验证结论对所画三角形是否成立？相互交流.

③教师用两只手打手势的方法（模仿直角三角形、钝角三角形和锐角三角形）让学生直观地感受结论.

（2）学生用文字语言表达自己的发现.

钝角三角形两条短边的平方和小于最长边的平方，锐角三角形两条短边的平方和大于最长边的平方，因此只有直角三角形的两条短边的平方和等于最长边的平方.

说明：实验四让学生知道，勾股定理是直角三角形特有的三边关系定理，其他三角形所不具有.

设计意图：在四次实验的基础上，学生意识到了研究的方法是从特殊的直角三角形到一般的直角三角形，从直角三角形到斜三角形，学生发现只有直角三角形才有勾股定理，进一步完善对勾股定理的表述，加深理解.

3.验证定理，解释内涵

（1）实验五：拼一拼.

①每人用4张全等的直角三角形纸片（两条直角边不相等）拼一拼，看看能否得到一个以c为一边的正方形？

②用你拼好的图形证明刚才的发现，请详细表达（预测会出现图7、图8两个图形）.

图7

图8

说明：当学生拼出以上两个图形后，指导学生如何抓住拼图的面积等量关系构建等式发现结论.学生自主选择证明其中一个.介绍赵爽弦图（图9）、北京召开的第24届国际数学家大会会标（图2）和总统证法（美国第20任总统加菲尔德的证明方法，如图10），都与“割”、“补”的方法有关.

图9

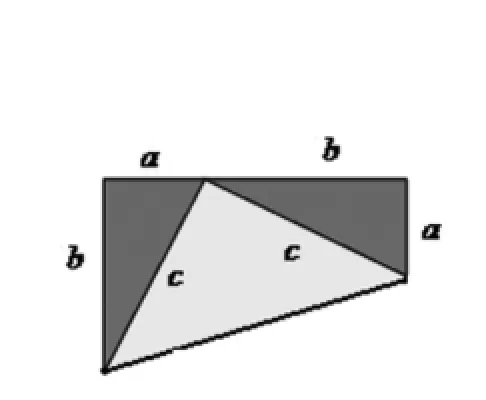
图10

图11

（2）归纳定理.

勾股定理：直角三角形的两条直角边的平方和等于斜边的平方.

几何语言：如图11，在△ABC中，因为∠C=90°，所以a2+b2=c2.

说明：勾股定理的本质是揭示了直角三角形三边的平方之间的等量关系.

（3）引导学生推导出勾股定理的变式和简便计算方法.由a2+b2=c2，可得a2=c2-b2=（c+b）（c-b），b2=c2-a2=（c+a）（c-a）.

（4）数学欣赏，动感体验.

①展示几何画板软件绘制的勾股树，如图12、图13所示.

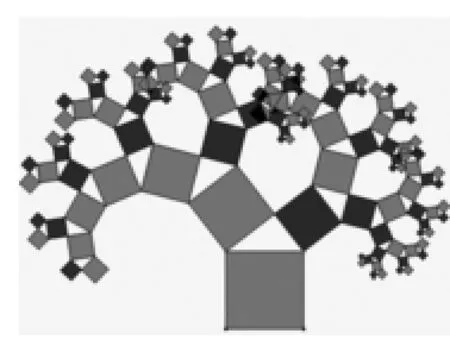
图12

图13

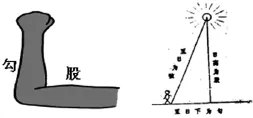
图14

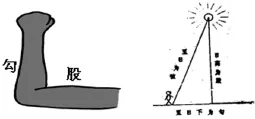
图15

②用几何画板演示勾股树，提问：如图13，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形边长是7 cm，则四个正方形A、B、C、D的面积之和是_______cm2，所有的正方形的面积之和是______cm2.试找出其中的规律.

说明：动态几何的引入更加直观地感受到勾股定理的魅力，探究几个正方形面积之和时运用到整体和转化思想，规律的探究突出从特殊到一般的思想.

（4）介绍勾股定理.

①勾股定理（公元前4000多年前）.

中国古代，人们把弯曲成直角的手臂的上半部分称为“勾”，下半部分称为“股”，后人还把直角三角形较短直角边称为“勾”，较长直角边称为“股”，斜边称为“弦”，如图14所示.

②商高定理（公元前1120年前后）.

公元前1120年前后，周朝数学家商高提出：将一根直尺折成一个直角，即有“勾三、股四、弦五”，记载于我国古代著名的数学著作《周髀算经》中.

③陈子定理（公元前700年前后）.

陈子和荣方讨论用勾股定理来测量太阳的高度，如图15所示，推广到一般的直角三角形.

④毕达哥拉斯定理（Pythagoras定理，公元前600年前后）.

两千多年前，古希腊的毕达哥拉斯学派首先发现了勾股定理，因此国外通常称勾股定理为毕达哥拉斯定理和百牛定理.

⑤在地球以外是否存在生命这个问题上，我国数学家华罗庚曾认为，如果外星人也拥有文明的话，我们可以用“勾股定理”的图形作为人类探寻“外星人”并与“外星人”联系的“语言”.

设计意图：概念教学不仅让学生明白知识“是什么”，更重要的是“为什么”.［3］定理的教学也是如此.通过拼图实验引导学生动脑动手验证和归纳勾股定理，并用几何语言表达出来.勾股树则体现了勾股定理与信息技术相结合的奇异美，勾股定理的历史介绍凸显了它的文化价值.

4.运用新知，体验成功

例1如图16，字母B所代表的正方形的面积是（）.

A.12B.13C.144D.194

变式：正方形B的边长等于多少？如何计算？

例2如图17，Rt△ABC中，∠C=90°，AB=c，AC=b，BC=a，若b=12，c=13，求a.

变式1：如图18，若D为AB的中点，试求CD的长与△CDA的面积.

变式2：若CE⊥AB于点E，求CE的长.

图17

图16

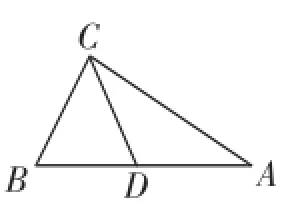
图18

例3观察国外数学爱好者设计的“流水版”勾股定理，如图19，试说明：为什么两个水箱中的水最后可以正好装满下面的水箱？

图19

说明：学生可能会解释为两个小的长方体水箱的体积之和等于大的长方体水箱的体积，若直角边分别为a、b，斜边为c，得到a3+b3=c3.因为三个水箱的厚度h相同，所以得到a2h+b2h=c2h，实际上是a2+b2=c2.如果都是正方体，可得a3+b3=c3.这里还可以进一步介绍费马大定理：当整数n>2时，关于x、y、z的方程xn+yn=zn没有正整数解.

设计意图：通过练习和变式训练，强化所学知识，通过变式提问，培养学生综合所学知识解决问题的能力.网络图片中的数学知识，也是验证了勾股定理在生活中最直观的体现，费马大定理是巧妙的拓展.

5.独立练习，巩固新知

例4已知一个直角三角形的两边长分别为3和4，则第三边长的平方是（）.

A.25B.14C.7D.7或25

例5如图20，△ABC中，AB=AC=5，AD⊥BC于D，BC=6，则AD=______.

例6如图21，Rt△ABC中，∠C=90°，D是AB的中点，若BC=6，CD=5，则AC=______，△ACD的面积=_____.