具有刚度非线性的结构系统阻尼参数测试

李 晖， 孙 伟， 刘 营， 韩清凯

(1.东北大学 机械工程与自动化学院，沈阳 110819； 2.大连理工大学 机械工程学院，大连 116024)

具有刚度非线性的结构系统阻尼参数测试

李 晖1， 孙 伟1， 刘 营1， 韩清凯2

(1.东北大学 机械工程与自动化学院，沈阳 110819； 2.大连理工大学 机械工程学院，大连 116024)

机械结构系统中存在大量的结构，其固有频率会随着激振力幅的不同而改变，称之为刚度非线性结构，例如螺栓法兰联接结构、涂层复合结构等。由于存在刚度非线性，经典的半功率带宽法无法准确辨识这些结构的阻尼参数。本文在修正经典半功率带宽法的基础上，提出了一种适用于弱刚度及强刚度非线性系统的阻尼辨识方法，称为频域带宽法。首先，基于刚度非线性结构系统的运动方程，分别推导了弱刚度非线性及强刚度非线性系统的阻尼辨识公式。进一步，提出了基于频域带宽法测试具有刚度非线性结构系统的阻尼参数的方法及流程，并讨论了扫频方向、扫频速度对测试结果的影响。最后，以具有软式非线性特征的硬涂层薄板为对象进行实例研究，获得了该薄板不同激励幅度下的阻尼参数。本文的研究可为精确建立类似结构的动力学响应分析模型提供参考。

刚度非线性；结构系统；阻尼测试；测试流程；频域带宽法

在振动和噪声控制中, 阻尼的测试有着重要的工程及学术意义。阻尼参数是振动响应、振动应力计算分析时必须输入的关键参数之一。获得的阻尼参数不仅可用于结构动力学的建模、响应预估和优化设计等环节，还可以用来评价和校验阻尼减振效果。近年来，随着对结构动力学特性预估精度要求越来越高以及阻尼减振技术的广泛应用[1-2]，结构系统的阻尼测试技术显得越发重要。

机械结构系统中存在大量的结构，其固有频率会随着激振力幅的不同而改变，使得测试获得的频域响应曲线不再对称于固有频率所在的轴线。这类结构称之为刚度非线性结构，例如螺栓联接结构[3]、导轨系统[4]以及车体中常见的搭接结构[5]，还有一些复合材料结构[6]也会表现出刚度非线性。

对于这些结构，经典的时域及频域阻尼辨识方法不再适用，因为经典的方法都是来源于线性假设。就半功率带宽法而言，由于结构的频域响应经常发生非线性跳跃现象，致使无法捕获峰值点所对应的频率以及半功率点频率，或者仅能获得部分半功率带宽法阻尼辨识所需要的频率点，导致该法难以辨识刚度非线性结构系统的阻尼。为此，需要研究上述刚度非线性结构系统的阻尼参数测试新方法。

一些学者尝试改进经典的时域法来获得这类结构系统的阻尼，例如, Reed等[6]提出将结构自由衰减时域信号划分为若干段，每段包含若干个振动峰值，进而从每段信号中辨识出对应一定振动幅度的阻尼及刚度。Patsias等[7]和Pearson等[8]也采用了类似的方法测试具有刚度非线性的涂层结构系统的阻尼。时域法辨识阻尼通常需要信号具有较高的信噪比，所获得的阻尼经常会由于噪声的干扰而导致测试结果不准确。

本文从频域角度研究具有刚度非线性的结构系统阻尼参数的辨识方法。所提出的方法与经典的半功率带宽法相似，所以称之为频域带宽法。首先，将刚度非线性结构分为弱刚度非线性系统和强刚度非线性系统，并分别推导了基于频域带宽法的这两类系统的阻尼辨识公式。然后，提出了基于频域带宽法测试具有刚度非线性结构系统的阻尼参数的方法及流程，并讨论了扫频方向、扫频速度对测试结果的影响。最后，以具有软式非线性特征的硬涂层薄板为对象进行实例研究，获得了该薄板不同激励幅度下的阻尼参数。本研究可为精确建立类似结构的动力学响应分析模型提供参考。

1 辨识刚度非线性结构阻尼参数的原理

线性结构的频域响应曲线，其相对于固有频率所在的轴线(对称轴)总是左右对称；而具有刚度非线性的结构系统，其频域响应不再具有上述特点。对于弱刚度非线性结构系统，其对称轴一侧的频域响应曲线会出现较为陡峭的斜坡(见图1)。随着对称轴一侧的曲线陡峭程度的增加，其会变为强刚度非线性系统(见图2)。由于模态阻尼比是最常用的表征结构系统阻尼特性的参数，下面分别推导上述两类非线性系统的阻尼比辨识公式。

图1 弱刚度非线性系统Fig．1Theweakstiffnessnonlinearsystem图2 强刚度非线性系统Fig．2Thestrongstiffnessnonlinearsystem

1.1 弱刚度非线性系统

以下以单自由度系统为例，说明频域带宽法测试阻尼的原理。虽然机械结构系统一般为多自由度系统，但按照模态理论解耦后仍可将其变成若干单自由度系统。对于单自由度且具有刚度非线性的结构系统，其运动方程可表示为

(1)

式中：m为系统的质量，c为系统的等效粘性阻尼系数，k为系统的线性刚度，ε为小参数，F0为激振力幅度，ω为激振频率，Φ{X}为响应幅度X的单调函数，一个响应幅度对应一个函数值，当响应幅度X=0时，Φ{X}=0。

式(1)可进一步变换为

(2)

与式(2)相对应的线性系统为

(3)

线性系统的响应幅度可表示为

(4)

参照线性系统，该非线性系统的响应幅度可表示为[9]

(5)

设在扫频激励幅度F0的作用下，最大响应振幅对应的固有频率为ωR。对于小阻尼系统，ωR可表示为

(6)

式中：Xmax为扫频响应的最大振幅。

由式(6)可知，εΦ{Xmax}可以通过测试不同激励幅度F0下的Xmax和ωR来获得，辨识公式可表示为

(7)

由式(7)可知，输入一个Xmax，就会得到一个εΦ{Xmax}函数值，由这些数据点可拟合出εΦ{X}的函数表达式。由式(5)还可进一步得到无量纲响应幅度A的表达式，即

(8)

对式(8)进行分析可知，无量纲响应幅度A取得最大值的条件为：①ω/ω0=1，即外激励频率与系统的固有频率相等)；② 函数εΦ{X}≈0，此时可以进一步得到无量纲响应幅度最大值为

Amax≈1/2ξ

(9)

(10)

(11)

式(10)减去式(11)可得

(12)

式(10)加上式(11)可得

(13)

(14)

式(14)即为具有弱刚度非线性系统的阻尼辨识公式。只要在频域响应曲线上找到ωn和ωm，便可以精确识别出弱刚度非线性系统的阻尼比。

当εΦ{rXmax}=0时，则式(14)退化为线性系统的辨识公式，即

(15)

(16)

1.2 强刚度非线性系统

由于系统中非线性因素的增强，此时，由实验所测的频域响应曲线可能无法找到带宽频率点ωn(对应于软式非线性)或ωm(对应于硬式非线性系统)，如图3所示。此时，需要重新修正辨识式(14)。

图3 软式和硬式非线性系统分别对应的频域响应曲线Fig.3 Frequency response of the softening and hardening nonlinear systems

对于强软式非线性系统，由式(7)和式(14)，可获得用ωR及ωm表示的ωn，表达为

(17)

将式(17)代入式(14)，可获得具有强软式非线性系统阻尼比的辨识公式

(18)

类似的，可获得强硬式非线性系统阻尼比的辨识公式

(19)

综上，式(14)、式(18)、式(19)即为本文推导的面向具有刚度非线性的结构系统的频域带宽法阻尼辨识公式。一般结构系统均为多自由度系统，但是假如各阶模态耦合不严重，或者说某阶频率的共振峰非常明显，则可以用本文提出的方法来获得具有刚度非线性结构的各阶模态阻尼比。

2 具有刚度非线性结构的阻尼测试方法及流程

按照第1部分提出的频域带宽法阻尼辨识公式，测试具有刚度非线性的结构系统的阻尼，需要通过5个关键步骤：

(1) 测试结构系统的固有频率，确定扫频区间

为了有效获得结构系统的阻尼参数，首先需要获取各阶固有频率值，进而明确扫频测试时的频率区间。为了测试方便，可采用锤击法获得结构系统的各阶固有频率。进一步选择包含某阶固有频率的一小段频率区间(如80%～120%)作为扫频区间。扫频区间的选取要遵循：在能够有效辨识阻尼的前提下，频率区间越小越好。实测的系统通常为小阻尼系统，通常几十赫兹的频段就能满足阻尼测试的需求。

(2) 判断结构系统刚度非线性类型，确定扫频方向和速度

基于所确定的扫频区间，在不同激振力幅下，分别按照从高到低和从低到高的方向进行扫频测试。如发现随着激振力幅的增大，固有频率降低，则可确定为软式刚度非线性，反之则可认为是硬式刚度非线性。

扫频方向是影响阻尼辨识精度的一个重要因素，对于不同的非线性类型，所需要的扫频方向也不一样。以图4所示的强软式刚度非线性结构系统为例加以说明。若对该系统由低到高扫频测试，则实际测试时观测到的频域响应将从B点直接跳跃到D点，这样就无法获得系统最大响应幅度Xmax以及所对应的固有频率ωR，因而无法进行阻尼辨识。相反，若对该系统由高到低扫频测试，则频域响应将从C点跳跃到A点，虽然无法得到ωn，但系统最大响应幅度Xmax以及所对应的固有频率ωR均可以准确获得，根据式(18)还是可以辨识出该结构系统的阻尼。

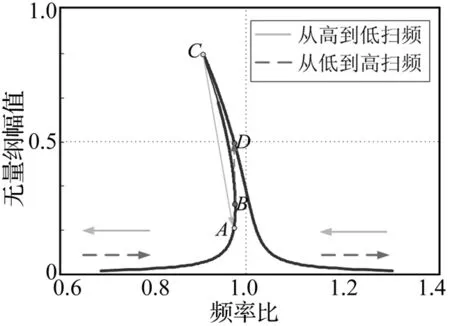
图4 强软式刚度非线性结构系统的频域响应Fig.4 Frequency response of strong softening stiffness-nonlinear system

由上述分析可知，对于具有强软式刚度非线性的结构，为了有效测试阻尼，应按照从高到低的扫频方向进行测试。与之相反，对于具有强硬式刚度非线性的结构系统，则需按照从低到高的扫频方向进行测试。

扫频速度同样对阻尼测试的精度有着重要的影响。由于所提的阻尼辨识方法是以系统的稳态响应为前提的，需要消除瞬态振动的影响。因此，必须合理确定的扫频速度，参照文献[9]，扫频速度的限定条件为

(20)

其中:S为允许的扫频速度，单位为Hz/s，Sm为最大扫频速度，fi为结构系统第i阶固有频率。只有满足式(20)要求的速度参数才能达到消除瞬态振动的目的。同时，还有必要选择更慢的扫频速度，并与满足式(20)的扫频速度进行比较验证，若两种速度参数下测试获得的固有频率非常接近，则可以将选择的扫频速度作为正式测试之用；否则，还应进行比较，直到两者获得的频率结果相差不大为止。

(3) 进行不同激振力幅下的扫频测试

改变激励幅度，根据步骤(1)中确定的频率区间进行扫频测试。为了提高扫频测试的精确性，防止信号受到其它干扰因素的影响，在每个扫频区间内应至少测试三次，并挑选信噪比最好的一组原始数据进行数据处理。需要说明的是，在实际测试时通常获取的是时域响应信号，为了采用频域带宽法测试阻尼，需要将将整个时域响应数据划分为若干时间段，对每个时间段的时域响应数据进行FFT变换，在整个扫频区间内，将每个时间段的FFT变换后的频率作为x轴，不同时间段的频域响应峰值作为y轴，经插值平滑处理后，获得扫频测试下的频域响应曲线。

(4) 拟合出单调函数εΦ{X}的表达式

由测试获得的不同激励幅度下某阶固有频率附近的扫频响应，确定每个激振力幅下的固有频率ωR以及所对应的峰值响应Xmax，参照式(7)，通过多项式拟合方法来获得单调函数εΦ{X}的表达式。

(5) 辨识出具有刚度非线性的结构的模态阻尼比

观测每个激振力幅下频域响应曲线关于固有频率所在的对称轴的对称性以及曲线的陡峭程度，判断指定激振力幅下该结构系统刚度非线性的强弱，若属于弱刚度非线性系统，则利用式(14)进行参数辨识;若属于强刚度非线性系统，则按照刚度非线性的类型利用式(18)和式(19)进行阻尼参数的辨识。

3 测试实例

按照“(2)”所述的测试方法及流程，对硬涂层薄板复合结构进行阻尼测试。薄板的几何尺寸为152 mm×110 mm×1.5 mm，材料为钛合金Ti-6Al-4V，弹性模量为110.32 GPa，泊松比为0.31，密度为4 420 kg/m3，采用等离子喷涂工艺在钛板的一侧全部涂敷MgO+Al2O3硬涂层，涂层的厚度为84 um。通过图5所示的夹具夹紧并使其处于悬臂状态，夹持区长度为40 mm。也可利用该夹具来夹紧其它厚度的硬涂层薄板，以实现具有不同非线性强度的结构系统阻尼参数的测量。需要说明的是，为了避免接触式测量方式对结构的阻尼参数的影响，选择了非接触式激光测振仪(Polytec PDV-100)，并组建了如图5所示的测试系统，主要仪器包括金盾EM-1000 F电磁振动台，PCB 086C01型力锤和LMS 16通道便携式数据采集仪等。当然，也可以选择其它类型的振动测试与采集设备来获取该结构的非线性刚度特征，因为非线性特征并不取决于测试仪器的精度，而是结构系统本身的一种典型特征。

图5 硬涂层悬臂薄板复合结构的阻尼测试系统Fig.5 Damping test system of hard-coating cantilever thin plate

表1 锤击法获得的硬涂层悬臂薄板固有频率

图6 不同激励幅度下扫频测试获得的硬涂层悬臂薄板的第4阶频域响应曲线Fig.6 Frequency response of hard-coating cantilever thin plate under different exciting level by sweep test

进一步，将对应各激励幅度的固有频率以及锤击法获得的第4阶固有频率代入到式(7)，可获得不同激励幅度下的单调函数值，同样列在表2中，式(21)为通过多项式拟合方法最终获得第4阶单调函数的表达式。

εΦ{X}4=-1.10×10-10X5+
1.18×10-8X4-3.23×10-7X3-
3.47×10-6X2+3.87×10-5X

(21)

在1 g，2 g，3 g激励幅度下硬涂层悬臂薄板复合结构的模态阻尼比可以通过具有弱刚度非线性系统的阻尼辨识公式(14)来获得,但对于4 g和5 g激励幅度下对应的频域响应曲线，由于无法找到左侧的带宽频率点ωn，因此这两个激励幅度对应的模态阻尼比需根据式(18)来进行辨识，获得的阻尼结果一并列于表2中。

表2 不同激励幅度下扫频测试获得的硬涂层悬臂薄板的第4阶固有频率、响应峰值、单调函数值及模态阻尼比

4 结 论

本文提出了一种适用于弱刚度及强刚度非线性结构系统的阻尼辨识方法。

(1) 对经典半功率带宽法进行了修正，分别推导了弱刚度非线性系统和强刚度非线性系统阻尼参数的辨识公式。可在仅获得峰值点对应的固有频率ωR和一个rXmax幅值对应的带宽频率点ωm或ωn的基础上，对强刚度非线性系统的阻尼参数进行辨识。

(2) 提出了测试具有刚度非线性结构系统阻尼参数的测试方法及流程。包括5个关键步骤：① 测试结构系统各阶固有频率；② 判断结构系统非线性类型；③ 进行不同激振力幅下的扫频测试；④ 拟合出单调函数εΦ{X}的表达式；⑤ 辨识出具有刚度非线性的结构系统的模态阻尼比。

(3) 以具有软式刚度非线性的硬涂层悬臂薄板为研究对象,并利用所提出的测试方法对其阻尼参数进行了测试，以第4阶阻尼为例，辨识出了不同激励幅度下的模态阻尼比。

[1] 尹帮辉，王敏庆，吴晓东.结构振动阻尼测试的衰减法研究[J].振动与冲击,2014,33(4):100-106. YIN Bang-hui, WANG Min-qing, WU Xiao-dong. Decay method for measuring structural vibration damping[J].Journal of Vibration and Shock,2014,33(4):100-106.

[2] Blackwell C, Palazotto A, George T J, et al. The evaluation of the damping characteristics of a hard coating on titanium[J]. Shock and Vibration, 2007,14(1): 37-51.

[3] Argatov I I, Butcher E A. On the Iwan models for lap-type bolted joints[J]. International Journal of Non-Linear Mechanics, 2011,46(2): 347-356.

[4] Ohta H, Tanaka K. Vertical stiffnesses of preloaded linear guideway type ball bearings incorporating the flexibility of the carriage and rail[J]. Journal of Tribology, 2010,132(1):1-9.

[5] Pearson I T, Mottram J T.A finite element modelling methodology for the non-linear stiffness evaluation of adhesively bonded single lap-joints: Part 1. Evaluation of key parameters[J]. Computers and Structures 2012, 90-91: 76-88.

[6] Ribeiro P, Akhavan H. Non-linear vibrations of variable stiffness composite laminated plates[J]. Composite Structures, 2012, 94(8): 2424-2432.

[7] Reed S A, Palazotto A N, Baker W P. An experimental technique for the evaluation of strain dependent material properties of hard coatings[J]. Shock and Vibration, 2008,15(6): 697-712.

[8] Patsias S, Saxton C, Shipton M. Hard damping coatings: an experimental procedure for extraction of damping characteristics and modulus of elasticity[J]. Materials Science and Engineering, 2004,370(1): 412-416.

[9] Torvik P J. Onestimating system damping from frequency response bandwidths[J]. Journal of Sound and Vibration, 2011,330(25): 6088-6097.

Damping identification for stiffness-nonlinearity structures

LI Hui1, SUN Wei1, LIU Ying1, HAN Qing-kai2

(1.School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China; 2. School of Mechanical and Engineering, Dalian University of Technology, Dalian 116024, China)

There are a large number of structures, whose natural frequencies will vary with the exciting levels and they can be named as the stiffness-nonlinearity structures, such as the bolted joint structures, composite laminated plate structures, etc. Due to the effect of stiffness-nonlinearity, the classical time domain and frequency domain methods for damping identification will not be still suitable. Therefore, on the basis of modifying the classical half-power bandwidth method, a method used to identify the damping of weak or strong stiffness-nonlinearity structure systems was presented. Based on the motion equation of the stiffness-nonlinearity system, the formulas for damping identification were derived respectively for the weak and strong stiffness-nonlinearity structure systems. Then, a damping test procedure was proposed for the above mentioned nonlinear structure systems. The test case of a hard-coating cantilever thin plate with soft nonlinear characteristic was provided, where the damping parameters were obtained under different exciting levels by sweep test and the practicability and effectiveness of the method proposed was demonstrated.

stiffness-nonlinearity; structure system; damping test; test procedure; frequency bandwidth method

国家自然科学基金资助项目(51375079)

2013-11-08 修改稿收到日期：2014-05-29

李晖 男，博士，讲师，1982年11月生

韩清凯 男，博士，教授，1969年3月生

TB53

A

10.13465/j.cnki.jvs.2015.09.024