物质点法在风与膜结构耦合作用中的应用研究
2015-03-17孙芳锦张大明
孙芳锦, 梁 爽, 张大明
(1.辽宁工程技术大学 建筑工程学院, 辽宁 阜新 123000; 2 辽宁工程技术大学 经济管理学院, 辽宁 阜新 123000)
物质点法在风与膜结构耦合作用中的应用研究
孙芳锦1, 梁 爽1, 张大明2
(1.辽宁工程技术大学 建筑工程学院, 辽宁 阜新 123000; 2 辽宁工程技术大学 经济管理学院, 辽宁 阜新 123000)
为克服常用数值方法在风与膜结构的耦合计算中网格易畸变、耗费机时大的缺点,提出采用物质点法计算风与膜结构的耦合作用。结构域采用物质点法描述,流体域采用浸入边界法描述。结构对流体的作用通过对结构最边缘的网格节点施加边界条件来实现,流体对结构的作用通过在结构表面施加压力和剪力实现。分别给出了结构域、流体域和流固耦合计算的求解步骤。将该算法应用于二维膜结构的耦合计算,得到了结构响应和流体压力场等结果,与采用有限元法计算结果进行了对比,结果符合良好;同时与有限元法对比了计算效率,结果表明物质点法计算效率要高于有限元法。结果表明物质点法计算风与膜结构的流固耦合作用中可以得到准确的结果,且计算效率得到较大提升。
膜结构,流固耦合,物质点法,计算效率
膜结构柔性大、质量轻等特点导致了风荷载是其控制荷载。由于膜结构较强的几何非线性和材料非线性,风与膜结构的流固耦合作用是其抗风设计中需要重点解决也是尚未很好解决的问题。数值模拟是研究流固耦合问题的有效方法之一,数值求解风与膜结构流固耦合问题的关键问题之一是避免流体和结构交界面的网格过度变形,目前计算风与膜结构的流固耦合作用最常用的数值方法是有限元法、欧拉方法等, 这些方法在处理流固耦问题时常遇到网格畸变、界面追踪和对流项处理等困难[1],且网格划分或重新生成也带来了巨大的计算耗费,也易导致计算精度下降或计算意外终止。因此研究高效简便的数值方法求解风与膜结构的耦合作用一直是计算风工程领域被广泛关注的热点问题。
为克服上述传统方法的缺点,本文采用物质点法[2]求解风与膜结构的耦合作用。物质点法是一种无网格方法,物质点法的最大优势是非常适合处理像膜结构这样经历大变形的结构,它可以避免有限元法存在的网格畸变以及纠正网格畸变重新生成网格的巨额计算资源等问题。物质点法是一种将质点和网格联系起来的一种无网格方法,它采用互无关联的拉格朗日物质点离散结构或流体,在这些物质点上求解连续方程的所有变量,并采用规则的欧拉背景网格计算空间导数和动量方程, 从而实现了质点间的相互作用与联系, 并避免了网格畸变问题。Sulsky 等[3]首先采用该方法分析了刚体的大转动和弹性体的碰撞问题, 展现了物质点法潜在的优势。 此后, MPM 受到广泛关注并得到了持续地发展。物质点法的应用广泛,包括爆炸冲击问题[4-5],地质学[6-7],裂缝扩展分析[8],多相流分析[9]等。目前国内外尚没有将物质点法应用于风与膜结构流固耦合分析中的应用。
本文采用物质点法研究风与膜结构的流固耦合作用。结构域采用物质点法描述并给出求解步骤,考虑与流体域的数据交换,采用浸入边界法对流体域进行描述。浸入边界表面采用非结构三角形网格离散,这些表面网格节点构成了一系列拉格朗日控制点,用以描述膜结构的运动。给出了物质点法求解流固耦合作用的步骤。最后将该方法应用于二维膜结构与风的流固耦合分析中。
1 控制方程和边界条件
1.1 流体控制方程
为便于与物质点法描述的膜结构的数据交换,这里采用曲线坐标系下的浸入边界法描述空气流体,因曲线坐标系下的浸入边界法可以较好的处理边界附近的流体域计算,也便于结构域的边界处理。
空气流体的控制方程为N-S方程,在曲线坐标下采用浸入边界法可以表示为:
(1)
其中:

1.2 结构控制方程
这里对经历大变形的膜结构采用物质点法进行描述。浸入边界表面采用非结构三角形网格离散,这些表面网格节点构成了一系列拉格朗日控制点,用以描述膜结构的运动。膜结构的控制方程可以表示为:
(2)
(3)
其中:ρs是膜结构密度,σs是Cauchy应力张量,bs是指定体积力,vs=dus/dt是结构速度,us是结点位移,us=ds-Ds,ds是当前(已变形)位形上的物质点坐标,Ds是初始(未变形)位形上的物质点坐标。
对于膜结构,考虑膜材的材料非线性,其本构关系可用超弹性模型描述,则σs可以通过如下方式求得:
(4)

(5)
其中:c1和c2是材料特性常数,k是体积模量,
J1=E1(E3)-1/3,
J2=E2(E3)-2/3,J3=(E3)1/2
(6)
(7)
1.3 边界条件
在所有的浸入表面流体速度应满足
vf=vΩ, 在Ω上
(8)
其中:vΩ是浸入表面的速度。
结构表面的表面牵引力应满足。
σf·nΩ=pΩ,在Ω上
(9)
其中:σf是流体应力张量,pΩ是牵引力向量,nΩ是表面Ω的法线向量。
2 求解方法
2.1 结构域的求解
结构方程采用物质点法进行求解。这里的物质点法采用无网格体系进行,物质点法认为结构域是由任意数量的物质点构成,物质点可以分为内部点和外部点(针对结构表面而言)。
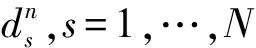
对于膜结构,物质点的质量可以定义为:
(10)
其中:h0是膜结构的厚度,ΔSi是第i个单元的表面积,Ni是离散膜结构的单元数量,这里的变量在每一时间步进行更新以满足式(3)。在每一时间步里,将物质点的信息向背景计算网格进行内插值计算求解结构方程,该背景网格选定在Cartesian坐标下。
在每一时间步采用物质点法求解结构域的过程可以归纳为:
(1) 对于每个物质点对其进行背景网格上的映射计算,
(11)
(2) 将动量从物质点向包含这些质点的单元节点进行映射,
(12)
(3) 求得在背景网格上每个点的内力向量,对于膜结构采用三角形单元离散,则有
(13)
其中:

(4) 根据动态边界条件(9)求得背景网格的外力向量,
(14)
并更新节点速度,
(15)
(5) 将当前速度再映射回给物质点,并计算物质点当前的位移和位置,
(16)
(17)
(18)
(6) 将物质点的位移映射回给背景网格,并计算时间步Δt内的变形梯度矩阵,
(19)
(20)
(7) 计算从t=0到t+tn+1的变形梯度矩阵、Green-Lagrangian应力张量以及应力,
(21)
(22)
(23)
可以看出,物质点法将在每一时间步内定义结构新的速度和位置,求得的数值将传递给流体域进行计算。
2.2 流体域的求解
流体域的求解主要采用文献[10]的方法,该方法将压力法和虚拟压缩法相结合,采用四阶Runga-Kutta方法计算求得对角线压力算子,再进行方程求解。受篇幅所限,详细步骤可参考文献[10]。
2.3 流固耦合算法
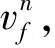


(4) 根据物质点新的位置和压力,求解结构周围新的流体方程,主要是估计浸入边界节点的速度和压力。这里采用的主要数值方法是将浸入边界看成是零厚度单元进行处理,根据结果表面已知解和流体节点,沿已经定义好的结构法线方向重新构造解,将边界条件应用于浸入边界附近的节点上。为方便任意复杂浸入边界解的重构,采用与结构附近类似的三角形非结构网格离散浸入边界。
3 算例分析
这里采用上述方法对一膜结构与风的流固耦合作用进行了研究。该膜结构由受重力作用的弹性膜结构屋盖和两个用以支撑膜屋盖的竖向刚性墙构成。膜结构的计算简图如图1所示。膜结构的厚度为0.01 m,密度为ρ=1.0×103kg/m3,弹性模量E=1.0×109N/m3,泊松系数ν=0,空气流体的密度ρ=1.25 kg/m3,粘性系数μ=0.1 Ns/m2,入口风速为13.75 m/s,特征长度,即膜结构的长度l=10 m,因此雷诺数Re=1 700。这里未考虑湍流影响。
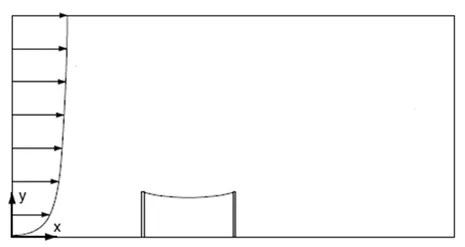
图1 膜结构计算简图Fig.1 Computation sketch for membran structure

图2 膜结构表面的物质点示意Fig.2 Material points sketch on the membrane structure
物质点方法中,膜结构表面由所有独立的物质点共同定义的。采用物质点法模拟流固耦合问题的基本思路与其他类型的物质点法模拟是一致的,区别是在流固耦合问题中,一些物质点是膜材的,余下的物质点是流体的。膜材的初试质量是通过输入膜结构密度、膜材厚度和用户指定点间距确定的。流体对结构的作用或结构对流体的作用是通过求解每个网格节点的动量方程确定的。膜结构表面的物质点示意如图2所示。流体域的离散使用了19 486/44 818个三角形单元/节点,时间步Δt=1.0×10-4s,膜结构时间步Δt=5×10-4s,经过试算,这种网格尺寸是独立的,即对最后的计算结果无影响。计算中共使用了5次子迭代。
图3分别给出了膜结构中点竖向位移时程和膜结构后方流体竖向速度时程,从图中可以看出,经过初试阶段后膜结构的响应趋于规律性的变化,这是由于经历初试阶段后,漩涡开始以接近膜结构基本频率从膜结构前缘脱落,这也导致膜结构响应和空气漩涡间存在较强的流固耦合作用。

图3 膜结构中点竖向位移和流体竖向速度时程Fig.3 Time histories of structure vertical displacement and fluid vertical velocity

表1 膜结构响应统计值比较
为了说明本文方法的计算效率,将本文的物质点法的计算效率与采用有限元法的计算效率进行了对比,如表2所示。
表1中给出了采用本文方法与采用有限元法计算得到的结构响应参数的比较,表1 中给出了采用本文方法与采用有限元法计算得到的结构响应参数的比较,其中有限元法的流体网格为26 957个,计算残差小于等于10-4时认为计算收敛。从表中可以看出,采用本文的物质点法计算得到的膜结构响应与有限元法计算结果非常接近,证明了本文方法的正确性。

表2 不同方法计算效率对比
从表2中可以看出,采用本文的物质点法达到收敛于指定值所需迭代次数要远小于有限元法,计算效率提高约42%;在经历同样的迭代次数后,物质点法的计算残差要小于有限元法计算残差,说明采用本文物质点法的计算效率要高于一般的有限元法,这主要是由于物质点法对于流固交界面处的变形处理方法较简单,因为只需处理膜结构表面的物质点,而无需像有限元方法那样处理大量的网格变形问题,这样就节省了较多的计算资源,简化了问题。
图4和图5分别给出了瞬时压力场分布和速度场分布。从图中可以看出,漩涡沿着膜结构的前缘脱落,并形成了典型的涡街。同时可以看出当漩涡经过尾缘时并没有在结构壁面的下游形成回流。值得注意的是,本例中的漩涡脱离现象主要是由膜结构的振动引起的,因为膜结构屋盖表面的压力变化过小,如果没有结构的振动是不会形成漩涡的。
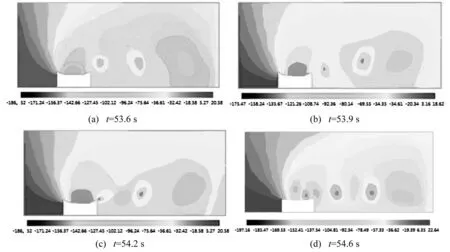
图4 不同时刻瞬时压力图Fig.4 Instantaneous pressure at different time

图5 膜结构周围速度场 (t=55)Fig.5 Velocity field around membrane structure
4 结 论
本文采用物质点法求解风与膜结构的耦合作用,采用物质点法描述膜结构并求解,为适应与物质点法在交界面处的数据交换,流体域采用浸入边界法进行描述,分别给出了物质点法求解结构方程和流固耦合作用的求解步骤,并将该方法应用于二维膜结构的耦合分析中,得到了较理想的结果,包括结构响应和流场压力、速度等分布;计算对比发现物质点法的计算效率要高于有限元法。计算证实了物质点法在风与膜结构耦合分析中的准确性和高效性,物质点法最大的优点在于避免了有限元法中对于交界面处网格的繁琐计算,大大提高了准确性和计算效率。本文目前只是将其应用于二维算例中,后续研究应进一步将其扩展到三维膜结构的耦合计算中。另外计算中发现在计算膜结构内力和速度时有时会出现计算不稳定性,因此如何提高计算过程中的稳定性也是值得进一步研究的问题。
[1] 刘欣.无网格方法[M].北京: 科学出版社, 2011.
[2] Sulsky D, Schreyer H L. Axisymmetric form of the material point method with applications to upsetting and taylor impact problems[J]. Computer Methods in Applied Mechanics and Engineering, 1996, 139 (1-4): 409-429.
[3] Sulsky D, Chen Z, Schreyer H L. A particle method for history-dependent materials[J]. Computer Methods in Applied Mechanics and Engineering, 1994,118(1-2): 179-196.
[4] Hu W, Chen Z, Model-based simulation of the synergistic effects of blast and fragmentation on a concrete wall using the MPM[J]. Int. J. Impact Eng,2006,32 (12):2066-2096.
[5] Lian Y P, Zhang X, Zhou X, et al., Numerical simulation of explosively driven metal by material point method[J]. Int. J. Impact Eng, 2011, 38 :237-245.
[6] Zhang H W, Wang K P, Chen Z, Material point method for dynamic analysis of saturated porous media under external contact/impact of solid bodies[J]. Comput. Meth. Appl. Mech. Eng, 2009, 198: 1456-1472.
[7] Andersen S, Andersen L. Modelling of landslides with the material-point method[J].Comput. Geosci,2010, 14: 137-147.
[8] Nairn J A. Material point method calculations with explicit cracks[J]. Comput. Model Eng. Sci.,2003, 4: 649-663.
[9] Zhang D Z, Zou Q, VanderHeyden W B, et al, Material point method applied to multiphase flows[J] J. Comput. Phys,2008, 227: 3159-3173.
[10] Sotiropoulos F, Constantinescu G. Pressure-based residual smoothing operators for multistage pseudo-compressibility algorithms[J]. Journal of Computational Physics,1997,133(1):129-145.
Application of material point method in wind-membrane structure interaction
SUN Fang-jin1, LIANG Shuang1, ZHANG Da-ming2
(1. College of Architecture and civil engineering, Liaoning Technical University, Fuxin 123000, China;2. College of Economy & Management, Liaoning Technical University, Fuxin 123000, China)
Due to the disadvantages of mesh distortion and large computer time consuming in commonly used numerical methods, material point method (MPM) was proposed to deal with the wind-membrane structure interaction. The solid was described by MPM, whereas the fluid was described using immersed boundary method. The effect of the solid on fluid was taken into account through imposing boundary conditions on the immediate vicinity mesh nodes. The effect of the fluid on solid was taken into account by imposing pressure and shear stress on the solid surface. And the procedures for solving the solid equations, fluid equations and the fluid-structure interaction were presented respectively. The algorithm was applied to a 2D membrane structure interacting with wind. The results of structural responses and fluid pressure field were obtained, which are in good agreement with those obtained using finite element method (FEM). The computing efficiency was compared between MPM and FEM, where MPM shows better efficiency. It is shown that ideal results can be obtained in wind-structure interaction analysis by employing MPM, with great improvement in computing efficiency.
membrane structure; fluid-structure interaction; material point method; computing efficiency
国家自然科学基金(51108345);同济大学土木工程防灾国家重点实验室开放基金(SLDRCE-MB-04);辽宁省教育厅基金一般项目(L2013134);江苏省工程力学分析重点实验室(东南大学)开放课题基金项目资助
2013-11-01 修改稿收到日期:2014-04-21
孙芳锦 女,博士,副教授,1981年生
TU973
A
10.13465/j.cnki.jvs.2015.09.018
