两点支承结构多点输入地震响应简化算法与精度分析

赵 博， 王元清， 陈志华， 石永久， 江 洋

(1. 天津大学 建筑工程学院，天津 300072； 2. 清华大学 土木工程系 土木工程安全与耐久性教育部重点实验室，北京 100084)

两点支承结构多点输入地震响应简化算法与精度分析

赵 博1， 王元清2， 陈志华1， 石永久2， 江 洋2

(1. 天津大学 建筑工程学院，天津 300072； 2. 清华大学 土木工程系 土木工程安全与耐久性教育部重点实验室，北京 100084)

多点输入计算中，在考虑所有耦合项的完全二次项(CQC)组合法基础上，给出忽略相关耦合项的平方和平方根(SRSS)近似算法，并针对两点支承结构的特殊性，提出该类型结构拟静力响应的简化计算方法。以典型的两种两点支承结构为算例，分析SRSS近似算法的精度。计算结果表明，对于两点支承结构而言，SRSS算法的误差主要是因为忽略拟静力和相对动力耦合项所致，而忽略振型耦合项的误差较小；行波效应越强，近似算法的误差越大；但从实际工程结构的计算结果来看，在常见的波速范围内，两种近似算法的位移、内力的计算误差都分别在10%、15%以内。因此采用SRSS近似方法用于此类结构多点输入地震响应的计算是可行的。

地震响应；多点输入；两点支承结构；平方和平方根法

地震动存在行波效应、不相干效应、衰减、局部场地效应等空间效应[1]，当结构的平面尺寸较大时，地震动的空间变化效应将导致结构不同支座运动不一致，由此引出了大跨结构的多点输入地震响应问题。大跨度结构的结构形式和支承形式多种多样，有周边支承的双向大跨度结构，如大跨度网架、球面网壳等，也有单方向跨度较大的桥梁、拱、门式刚架等结构类型。现有研究结果表明，多点输入下不同类型结构的响应规律有很大的区别，针对具体结构类型开展多点输入响应研究是比较合理的[2]。两点支承结构是大跨度结构中支承形式最为简单的结构，计算多点输入效应时只需考虑两个不一致的支座地震动输入，因此多点输入结构响应规律也较简单，已有较多学者对不同结构形式的两点支承结构多点输入规律展开了研究[3-6]。

事实上，由于两点支承结构大多形式简单，动力特征明显，动力计算中忽略部分耦合项对结果精度的影响可能较小。因此首先以考虑所有耦合项(包括拟静力和相对动力耦合项、相对动力振型耦合项)的完全二次项(CQC)组合法为基础，给出不考虑或部分考虑耦合项的平方和平方根(SRSS)组合法的近似计算式，并根据两点支承结构支座位移产生的拟静力响应只与两支承的相对位移有关这一特点提出适用于两点支承结构的拟静力响应简化计算方法，计算量仅为原来的1/4，但并不影响计算精度。以两个典型的两点支承结构(拱桁架和门式桁架)为例，验证所提出简化算法的计算精度。

1 多点输入随机响应

1.1 CQC精确算法

假设结构具有n个自由度和m个支座约束自由度，在地震多点输入下，任意响应z可以写成拟静力响应zs和相对动力响应zd之和

z=zs+zd

(1)

(2)

(3)

式中：uk为第k个支座位移，ak为第k个支座单位位移引起的结构静力响应；ski为第k个支座位移引起的第k阶归一化振型坐标，bki为第k支座单位位移引起的第i阶振型响应。

Der Kiureghian等[7]基于随机振动理论推导出与式 (1)对应的响应功率谱、均方差σz、极值期望值(以下简称最大值)zmax等计算公式：

(1)响应功率谱Szz

其中右端三项分别代表拟静力响应功率谱，拟静力相对动力耦合项的互功率谱，相对动力响应功率谱。

(4)

(5)

(2) 响应均方差σz

式(4)在频域内积分，得到响应均方差σ其中σuk、σski、σslj分别是相应项的均方差，而ρukul、ρukslj、ρskislj表示各项相关系数，均由积分得到。

(3) 最大值zmax

零均值平稳随机过程的最大值zmax可由峰值系数pz和均方差σz的乘积估计

zmax=pzσz

(6)

于是，可由式(5)和式(6)计算响应最大值

(7)

其中:uk,max、slj,max等为各对应项的极值期望，puk、pslj为相应的峰值系数。

1.2SRSS近似算法

前述精确计算公式由随机振动理论推导而来，考虑了所有项之间的耦合作用，精度较高，但计算量很大。事实上，在某些特殊情况下，也可作一定简化，本节引入两个假定条件：

(Ⅰ) 结构自振频率大于0.5 Hz，即周期小于2 s。文献[7]指出，对于此类结构，式(5)、式(7)中拟静力和相对动力的耦合系数ρukslj很小，忽略该项带来的误差可能不大。

(Ⅱ) 结构自振频率分散。当结构频率分散时，振型耦合程度也较低，式中ρskislj(当i≠j时)也可忽略。

由此可定义两种近似计算方法：

(1) 近似方法一

假设仅满足假定条件(Ⅰ)，忽略拟静力和相对动力的耦合项，此时式(4)、式(5)、式(7)分别简化为

(8)

(9)

(10)

其中式(9)、式(10)可以理解为：分别求解拟静力响应和相对动力响应，总响应由两者的平方和平方根(SRSS)组合方法得到。

(2) 近似方法二

假设同时满足上述假定条件(Ⅰ)和(Ⅱ)，忽略相对动力响应中的振型耦合项，上述各式进一步简化为

(11)

(12)

(13)

式(12)、式(13)的计算步骤为：分别求解拟静力响应和各阶振型坐标的相对动力响应值，再将所有项采用SRSS方法组合得到总响应。

2 两点支承结构拟静力响应简化计算

对于两点支承结构而言，支座位移产生的拟静力响应只与两支承的相对位移有关，前文各式中拟静力响应还可进一步简化。观察式(4)右端第一项，即拟静力功率谱Szszs表达式

(14)

对于两点支承结构，式中:a2= -a1。展开式(14)

(15)

其中右端括号内为两支承处地面相对位移Δu的功率谱

SΔu=Su1u1(ω)-Su1u2(iω)-Su2u1(iω)+Su2u2(ω) (16)

对于同时考虑行波效应和不相干效应的情况，式(16)可由以下解析式快速计算得到

(17)

式中:d为两点间距，Su为地面位移功率谱，ρ(ω)和vapp分别为两点间相干函数和地震波视波速。

因此，拟静力响应可由地面相对位移计算

(18)

(19)

(20)

采用简化计算方法后的式(18)的计算量仅为式(14)的1/4。

根据前述推导过程，概括出两点支承结构同时采用拟静力响应简化计算法和SRSS组合法的计算步骤：

(1)根据结构跨度和多点地震动参数计算两点支座处地面相对位移功率谱SΔu(式(17))，积分求得相对位移均方差σΔu、最大值Δumax。

(2) 固定一个支座，在另一支座处施加与步骤(1)得到的相对位移值相等的位移，静力求解，计算结构拟静力响应(式(18)～(20))。

(3) 计算结构相对动力响应，可以选择是否考虑振型耦合项。

(4) 采用SRSS法组合拟静力响应和相对动力响应，计算结构总响应。

3 算例分析

3.1 多点地震动参数

假定地震波传播和振动方向均沿结构跨度方向，考虑多点输入效应中的行波效应和不相干效应：

(1) 行波效应。在100～1 600 m/s范围内取10个视波速vapp进行计算：100、125、150、175、200、250、300、400、800、1 600。

(2) 不相干效应。采用常用的Luco-Wong[8]

(21)

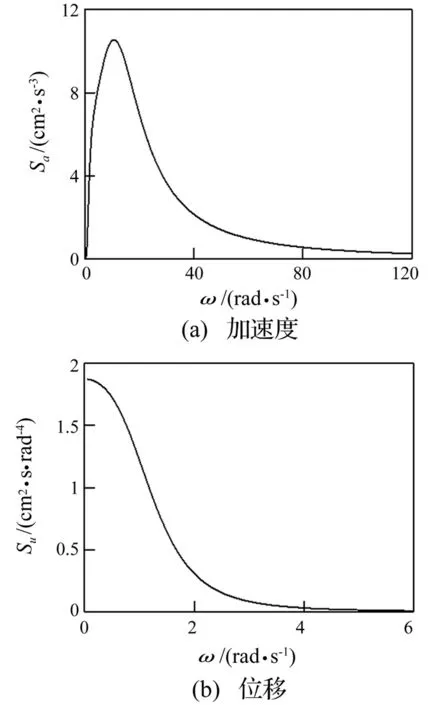
图1 地震动功率谱密度函数曲线Fig.1 PSD curve of ground motion

一致地震动加速度功率谱Sa(ω)采用Clough-Penzien谱[9]

(22)

其中:谱参数ωg= 13.96 rad/s，ζg= 0.8，ωf=1.396 rad/s，ζf= 0.8，S0=7.123 cm2/s3[10]。地震动加速度和位移功率谱曲线如图1所示。

3.2 拱桁架

选取钢管拱桁架模型如图2所示。跨度100 m，矢高25 m，两端铰支；采用倒三角形截面，截面宽度均为2 m，纵向节间长度约为2.8 m；上下弦选用Φ236×12圆钢管，腹杆选用Φ130×5圆钢管；重力荷载以构件自重和节点集中质量的形式施加，每个节点上定义500 kg的集中质量；结构阻尼比0.035。

图2 拱桁架模型Fig.2 Model of arch truss

图3是视波速vapp=400 m/s时，分别采用精确算法和两种近似算法计算得到的上弦杆节点相对位移(相对左柱脚)和上弦杆轴力在跨度方向的分布情况。图4的误差图进一步给出了两种近似计算方法的误差。

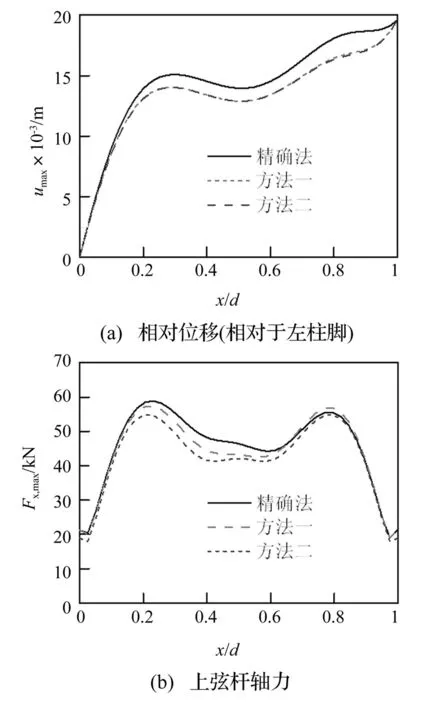
图3 结构响应最大值，vapp=400 m/sFig.3 Expected extreme value of response，vapp=400 m/s

图4 近似方法计算误差，vapp=400 m/sFig.4 Error of SRSS methods，vapp=400 m/s

很显然，忽略了拟静力和相对动力耦合项的近似算法一的计算结果普遍小于精确值，而进一步忽略振型耦合项的算法二的计算结果更小；两种近似算法的位移计算误差相当，内力计算误差相差较大。

图5给出了两种近似算法得到的各种结构响应误差绝对值的最大值随跨度与波速的比值(d/vapp)的变化情况。横坐标d/vapp越大则行波效应越强，而横坐标0处为波速无穷大、不考虑行波效应的计算结果。各图表明

(1) 两种算法的位移误差曲线吻合得较好，内力结果也较接近。这说明对于本算例的结构而言，近似算法导致的误差主要是因为忽略拟静力和相对动力耦合项所致，忽略振型耦合项的误差较小。

(2) 不同响应量的误差随波速的变化情况各不相同。位移误差随d/vapp增大出现波动情况，而结构内力响应误差总体呈增大趋势。

(3) 在常见的波速范围内(100～1 600 m/s)，两种算法的位移误差都在10%以内，而内力误差均控制在15%以内。

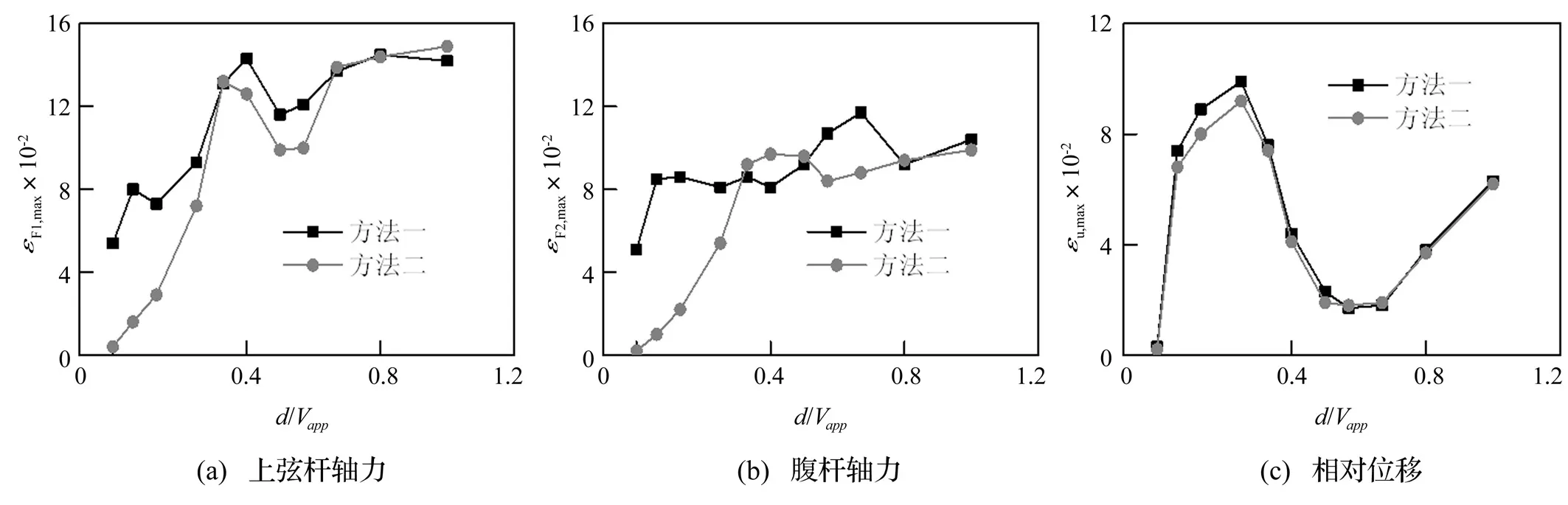
图5 近似方法误差最大值Fig.5 Maximum error of SRSS methods

3.3 门式桁架

选取钢管门式桁架模型如图6所示。跨度62.4 m，两端铰支；采用三角形截面，截面高2.8 m，宽2.2 m；根据设计要求，采用多种截面尺寸的圆钢管；重力荷载以构件自重和节点集中质量的形式施加，屋盖下弦节点上定义730 kg的集中质量；结构阻尼比0.035。

图7给出了各类响应误差最大值随波速的变化情况。计算结果与此前拱桁架的计算结果类似：

(1) 两种算法的位移误差曲线吻合得较好，内力结果有一定差别。

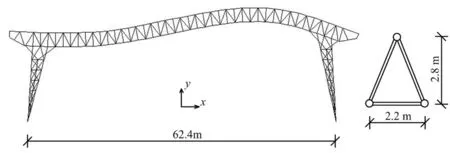
图6 钢管门式桁架模型Fig.6 Model of portal truss

(2) 总的来看，误差随d/vapp增大呈增大趋势。

(3)常见的波速范围内，两种算法的位移和腹杆轴力误差都在10%以内，而弦杆轴力误差在15%以内。

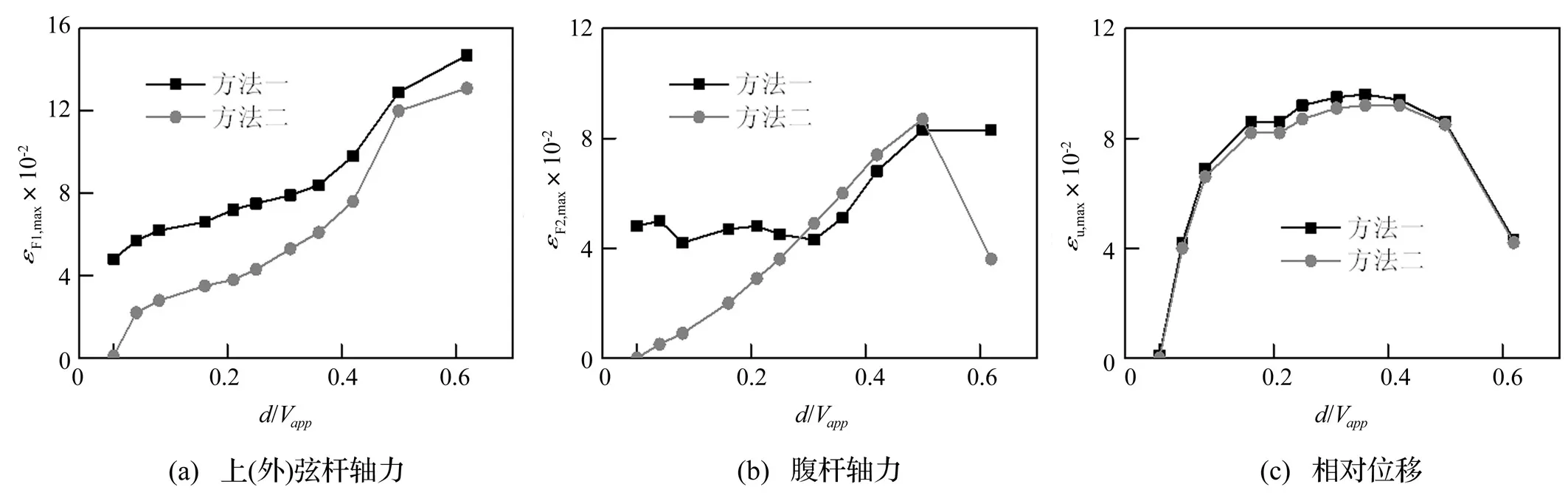
图7 近似方法误差最大值Fig.7 Maximum error of SRSS methods

4 结 论

(1) 简化的拟静力响应算法适用于两点支承结构，计算量减少为1/4。

(2) 对于两点支承结构而言，SRSS近似算法导致的误差主要是因为忽略拟静力和相对动力耦合项所致，忽略振型耦合项的误差相对较小。

(3) 行波效应越强，近似算法的误差越大。但从典型的拱桁架和门式桁架的计算结果来看，在常见的波速范围内，两种近似算法的位移、内力的计算误差都分别在10%、15%以内。因此采用SRSS近似方法用于此类结构多点输入地震响应的计算是可行的。

[1] Kiureghian A D. A coherency modal for spatiallyvarying ground motions [J]. Earthquake Engineering & Structural Dynamics, 1996, 25(1): 99-111.

[2] 江洋, 石永久, 王元清. 大跨结构地震多点输入响应研究进展[C]. 第17届全国结构工程学术会议论文集(第Ⅲ册), 2008: 47-56.

[3] Su Liang, Dong Shi-lin, Kato S. Seismic design for steel trussed arch to multi-support excitations[J]. Journal of Constructional Steel Research, 2007, 63(6): 725-734.

[4] 丁阳, 岳增国, 刘锡良. 大跨度张弦梁结构的地震响应分析[J]. 地震工程与工程振动, 2003, 23(5): 163-168. DING Yang, YUE Zeng-guo, LIU Xi-liang. Seismic response analysis of long-span beam string structures[J]. Earthquake Engineering and Engineering Vibration,2003, 23(5): 163-168.

[5] 江洋, 石永久, 王元清,等. 大跨门式钢管桁架结构多点输入地震响应分析[J]. 北京交通大学学报, 2009, 33(4): 88-93. JIANG Yang, SHI Yong-jiu, WANG Yuan-qing, et al. Seismic response analysis of large-span gate-type tube truss structures under multi-support excitation[J]. Journal of Beijing Jiaotong University,2009, 33(4): 88-93.

[6] Su Liang, Dong Shi-lin, Kato S. A new average response spectrum method for linear response analysis of structures to spatial earthquake ground motions[J]. Engineering Structures, 2006, 28(13): 1835-1842.

[7] Kiureghian A D, Neuenhofer A. Response spectrum method for multi-support seismicexcitations [J]. Earthquake Engineering & Structural Dynamics, 1992, 21(8): 713-740.

[8] Luco J, Wong H. Response of a rigid foundation to a spatially random ground motion[J]. Earthquake Engineering & Structural Dynamics, 1986, 14(8): 891-908.

[9] Clough R W, Penzien J. Dynamics of structures[M]. New York：McGraw-Hill, 1993.

[10] 薛素铎, 王雪生, 曹资. 基于新抗震规范的地震动随机模型参数研究[J]. 土木工程学报, 2003, 36(5): 5-10. XUE Su-duo, WANG Xue-sheng, CAO Zi.Parameters study on seismic random model based on the new seismic code[J]. China Civil Engineering Journal, 2003, 36(5): 5-10.

Accuracy analysis of a simplified algorithm for seismic response analysis of two supports structures under multi-support excitation

ZHAO Bo1, WANG Yuan-qing2, CHEN Zhi-hua1, SHI Yong-jiu2, JIANG Yang2

(1. School of Civil Engineering, Tianjin University, Tianjin 300072, China;2. Key Laboratory of Structural Engineering and Vibration of Education Ministry, Department of Civil Engineering, Tsinghua University, Beijing 100084, China)

On the base of response spectrum CQC method considering all the coupling items, an approximate SRSS algorithm ignoring relevant coupling terms was given. Due to the specialty of structures with two supports, a simplified algorithm for analysing quasi-static response of this type of structures was put forward. Taking a typical two supports structure as example, the accuracy of the approximate algorithm of SRSS was analyzed. The results show that the error of SRSS method mainly comes from ignoring quasi-static and relative dynamic coupling terms, but not modal coupling terms. The stronger the traveling-wave effect is, the bigger the error of the approximate algorithm will be. But according to the calculation results of actual engineering structures, within the range of the common wave velocity, the computation errors of displacement and internal force of the two approximate algorithms keep within 10% and 15% respectively. So it is feasible to use approximate algorithm of SRSS for seismic response analysis of two supports structures under multi-support excitation.

seismic response; multi-support excitation; two supports structures; sum of squares and square root (SRSS) method

国家自然科学基金重点项目(51038006); 高等学校博士学科点专项基金资助课题(20090002110045)

2013-12-05 修改稿收到日期：2014-05-09

赵博 男，博士生，1987年生

陈志华 男，博士，教授，1966年10月生

TU311.3; O327

A

10.13465/j.cnki.jvs.2015.09.004