高超声速飞行器巡航飞行控制器设计
2015-03-16赵林东唐胜景
赵林东, 唐胜景
(北京理工大学 宇航学院, 北京 100081)
高超声速飞行器巡航飞行控制器设计
赵林东, 唐胜景
(北京理工大学 宇航学院, 北京 100081)
针对高超声速飞行器高空高速巡航飞行时,其数学模型具有严重非线性、不稳定性及参数不确定性等特点,设计了包含法向过载指令跟踪的非线性鲁棒控制系统。通过忽略高度状态量并引入纵向过载的积分作为一个虚拟输出量,实现了非线性模型的完全反馈线性化和输入/输出解耦,推导出改进模型并基于滑模控制方法设计了鲁棒跟踪控制器。仿真结果表明,该改进模型是合理的,所设计的控制器能够很好地实现对法向过载指令的准确跟踪。
高超声速飞行器; 巡航飞行控制; 反馈线性化; 参数不确定性
0 引言
本世纪初,高超声速飞行器因其巨大的军民两用前景和代表了航空航天技术制高点的地位,再次引起了广泛的关注并得到深入研究。一般飞行速度超过马赫数5的飞行器被称为高超声速飞行器[1]。已有的研究表明,高超声速飞行器模型具有严重的非线性和各种耦合影响突出的特点,并且由于飞行速度很高,飞行器对飞行条件和参数的变化非常敏感[2],这对控制系统的设计提出了挑战。
动态逆是实现反馈线性化的一种重要方法,能够将原非线性系统补偿为具有线性传递关系的且已解耦的伪线性系统,然后利用线性系统的各种设计理论来完成伪线性系统的综合[3]。文献[4]针对通用高超声速飞行器纵向模型,利用动态逆方法得到伪线性模型,考虑不确定参数后设计了自适应滑模控制器,实现了对飞行高度和飞行速度指令的跟踪。文献[5]利用动态逆方法对吸气式高超声速飞行器(AHV)纵向模型进行了输入-输出反馈线性化,考虑不确定参数影响并设计了鲁棒控制器。文献[6-8]利用动态逆方法对非线性模型进行了反馈线性化处理。然而,上述研究中基本上是以跟踪飞行高度和飞行速度指令为控制系统的设计目标,没有考虑对法向机动过载的跟踪控制。对于需要进行机动飞行的高超声速飞行器,实现对法向过载指令的跟踪控制是必要的。
本文提出一种模型改进方法,并采用滑模控制方法设计了跟踪飞行速度指令和法向过载指令的鲁棒控制器。最后,考虑模型参数不确定性的影响,采用高超声速飞行器Winged-cone纵向模型进行仿真,验证了该控制方法的有效性。
1 高超声速飞行器模型
高超声速飞行器在不考虑弹性模态时,其刚体纵向模型方程基本一致,如Winged-cone模型[4]和AHV模型[5]。本文采用Winged-cone模型进行推导和仿真。Winged-cone模型是NASA用于研究高超声速飞行器的一种概念飞机,是高超声速飞行研究的一个标准模型,模型方程为[4]:
(1)
发动机模型[7]为:
式中:β为发动机节流阀调定值。文献[7]采用一个二阶系统模型来表示发动机的动态特性:
(2)

在上述模型中,控制量为发动机节流阀调定值βc和升降舵偏转角δe。
2 模型改进和控制器设计
2.1 动态逆控制方法
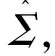
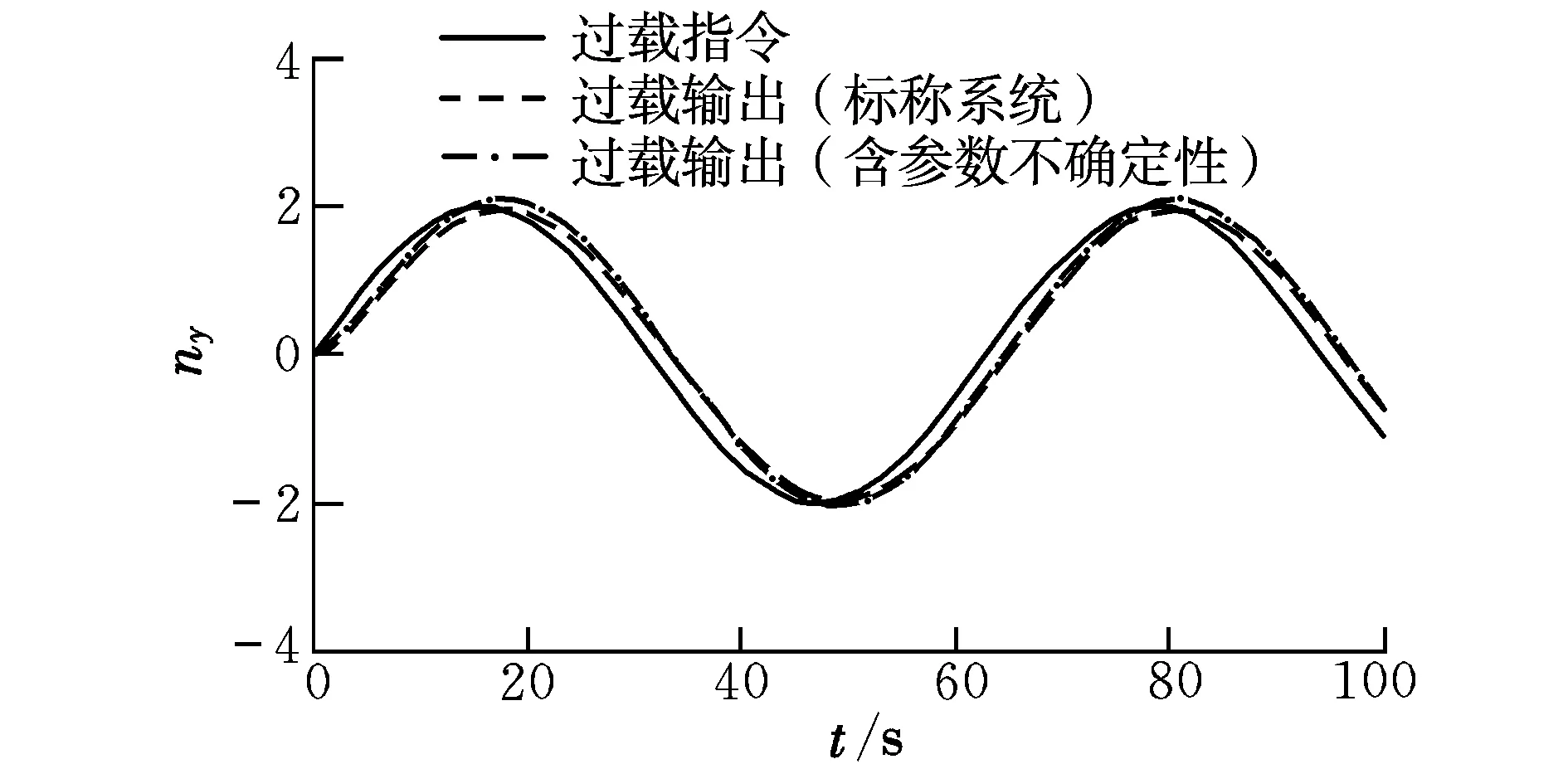
多输入-多输出系统的反馈线性化方法是对每一个输出通道yi关于时间连续求微分,直到微分子式中首次出现至少一个控制输入量为止,所有输出量的微分次数之和称为相对阶数[9],记为p。若非线性系统的阶数为n,则系统实现输入-输出完全线性化的充分必要条件是p=n;如果p 2.2 模型改进和反馈线性化 文献[4-8]使飞行器跟踪飞行速度改变指令Vd和飞行高度改变指令Hd,以V和H作为输出时恰好能实现完全线性化;而本文模型重点考虑在巡航飞行时飞行器能够快速准确跟踪法向过载指令。飞行器系统模型为5阶,发动机模型为2阶,故非线性系统模型的阶数为n=7,一般选用的状态量为: (3) (4) 即对过载只需求两次微分。若以飞行速度和法向过载为输出,输出量总的微分次数即相对阶数为p=5,小于系统阶数n,不满足完全线性化的条件。为了满足完全线性化条件,需要对模型做如下处理: (1)忽略高度状态 本文设定高超声速飞行器基准模型在高度为32 km的高空以Ma=15的速度作水平巡航飞行。对高超声速纵向模型在平衡点进行小扰动线性化,从推导结果中发现高度的改变对速度V、飞行路径角γ和飞行迎角α的影响如下: (5) =5.57×10-10 (6) =5.57×10-10 (7) 由式(5)~式(7)可知,关于高度H的偏导数只与μ,r,V和γ相关,由于高空(r很大)和高速(V很大),关于高度H的偏导数都非常微小。为了更详细分析高度带来的影响,进一步分析各偏导数之间的相对大小关系,令 (8) 则Θ中最后一列代表高度的影响,最后一列相对前面几列的相对值即可代表高度状态改变带来的相对影响强弱程度。在平衡点(γ0=0°,α0=1.779 7°)计算得: Θ= (9) 选取另一组飞行状态(γ=10°,α=15°),线性化并计算得: (10) 由式(9)和式(10)可知,飞行状态关于高度的偏导数相对于其他偏导数项来说非常小,相对值不足1%,忽略以后对其他状态量的影响不大。特别注意,在设计控制系统时忽略高度状态项,相当于仅忽略了高度变化对V,γ和α的直接影响项,而高度变化对大气密度和空气动力/力矩的影响没有做任何改变和忽略,其依旧存在于相应的气动模块中。 综上所述,本文忽略高度状态来建立改进模型并设计控制系统具有一定的合理性。此时非线性系统阶数为n=6,状态变量取为: (11) (2)虚拟输出量 忽略高度后系统模型的阶数减小为6阶,此时,输出量的相对阶数为5,仍然小于系统阶数。所以直接将法向过载作为输出量仍然不合适。 考虑法向过载的积分形式 (12) 若以Ny作为一个虚拟输出信号,则有: (13) (14) (15) (16) 其中: (17) 其中: 在式(17)中,fV和fN与控制输入无关,分析发现除了γ=90°的飞行状态以外,K-1都存在[4]。当K可逆时,可得: (18) 式(18)即为高超声速飞行器纵向非线性模型的逆系统。逆系统和高超声速飞行器纵向模型的原系统组合成为一个伪线性复合系统,其结构如图1所示。 图1 伪线性复合系统结构图Fig.1 Block diagram of composite pseudo-linear system 通过反馈线性化,原非线性系统被解耦成为具有线性关系且解耦的“α阶积分逆系统”,可以采用线性控制方法设计伪线性复合系统的控制器。 2.3 滑模控制器设计 基于前文推导的伪线性系统,采用滑模控制方法实现对飞行速度改变指令Vd和法向过载指令ny的跟踪。滑模面按控制性能需求设计,系统一旦进入滑模面后,其滑模运动就与被控对象的参数和外界干扰无关,因此滑模控制器具有较强的鲁棒性。 (19) 式中:a0,a1,b0为待定正常数,决定了系统到达滑模面的动态特性,需要根据实际情况调整。进一步联合式(17)得: (20) 其中: 考虑滑模到达条件和抑制抖振的需要,滑模趋近律选为带边界层饱和函数的形式: (21) 式中:k1和k2为正常数;Δ为边界层厚度,且 边界层厚度越小,控制增益越大,控制效果越好,但是抖振也越强;反之,边界层厚度越大,控制增益相对减小,抖振会得到抑制,但是控制效果会变差。所以,在使用时要根据实际情况合理选取边界层厚度。 由式(20)和式(21)可得最终的滑模控制律: (22) 从式(22)可知,滑模控制律包含两个部分,K-1[-v1,-v2]Τ为使系统状态保持在滑模面上对应的控制部分;K-1[-k1sat(sV/ΔV),-k2sat(sn/Δn)]Τ用来使因干扰或参数不确定引起的系统状态偏离滑模面后重新回到滑模面上的控制部分。使用上述控制律,即使存在不确定性干扰,也能保证系统运动轨迹到达滑模面。 利用Matlab & Simulink进行仿真实现,仿真时分包含和不包含参数不确定性两种情况进行。从0时刻起,考虑三种输入指令情况:(1)给定飞行速度阶跃指令Vd=50 m/s,法向过载指令为0,经过30 s后得到的仿真曲线如图2所示;(2)给定法向过载阶跃指令nyd=1,速度指令为0,经过30 s后得到的仿真曲线如图3所示;(3)给定速度指令为0,法向过载指令变化规律为ny=2 sin(0.1t),仿真100 s得到的曲线如图4所示。 由图2可知,在标称系统和含有参数不确定性时,飞行速度指令都得到了快速准确的跟踪,同时法向过载都极小,两个输出通道实现了良好的解耦。 由图3可知,法向过载指令在标称系统时得到了快速准确的跟踪,在存在参数不确定性时,法向过载有小于5%的稳态误差,同时速度的变化极小。 由图4可知,即使在存在参数不确定性的情况下,正弦变化的法向过载指令也能得到较为准确的跟踪。这说明本文的控制方法能够有效地实现对法向过载的准确跟踪,对参数不确定性具有一定的鲁棒性。另外,从图3可以看到,法向过载单位阶跃响应的上升时间约为8 s,而图4中正弦波形式的法向过载跟踪存在一定的相位滞后。这说明法向过载跟踪响应比较缓慢,主要是因为本文使用的高超声速模型的质量和转动惯量都很大且高空气动舵效率较低;也说明这类高超声速飞行器在高空高速巡航飞行阶段不适合进行快速剧烈的机动,但如图4中较慢的机动飞行是可行的。 图3 nyd=1时的响应曲线Fig.3 Response curves for nyd=1 图4 ny=2 sin(0.1t)时的跟踪曲线Fig.4 System tracking curves for ny=2 sin(0.1t) 本文针对通用高超声速飞行器纵向模型,提出了对法向过载进行跟踪控制时的完全反馈线性化问题,采用滑模控制方法设计了跟踪控制器,并进行了仿真验证。该法向过载跟踪控制器能够实现对速度和法向过载的准确跟踪,并具有一定的鲁棒性;同时,高超声速飞行器在高空高速巡航飞行时,不适合做快速剧烈的机动,但能够实现较为缓慢的机动飞行。 [1] Fidan B,Mirmirani M,Ioannou P A.Flight dynamics and control of air-breathing hypersonic vehicle: review and new direction [R].AIAA-2003-7081,2003. [2] Marrison C I,Stengel R F.Design of robust control systems for a hypersonic aircraft [J].Journal of Guidance,Control,and Dynamics,1998,21(1):58-63. [3] 李春文,冯元琨.多变量非线性控制的逆系统方法[M].北京:清华大学出版社,1991:2-6. [4] Xu H J,Mirmirani M D,Ioannou P A.Adaptive sliding mode control design for a hypersonic flight vehicle [J].Journal of Guidance,Control,and Dynamics,2004,27(5):829-838. [5] Gao G,Wang J Z.Reference command tracking control for an air-breathing hypersonic vehicle with parametric uncertainties [J].Journal of the Franklin Institute,2013,350(5):1155-1188. [6] Parker J T,Serrani A,Yurkovich S,et al.Control-oriented modeling of an air-breathing hypersonic vehicle [J].Journal of Guidance,Control,and Dynamics,2007,30(3):856-869. [7] Wang Q,Stengel R F.Robust nonlinear control of a hypersonic aircraft [J].Journal of Guidance,Control,and Dynamics,2000,23(4):577-585. [8] Lohsoonthorn P,Jonckheere E,Dalzell S.Eigenstructure vs constrainedH∞design for hypersonic winged cone [J].Journal of Guidance,Control,and Dynamics,2001,24(4):648-658. [9] 贺昱曜,闫茂德.非线性控制理论及应用[M].西安:西安电子科技大学出版社,2007:110-115. (编辑:李怡) Cruise flight controller design for a hypersonic vehicle ZHAO Lin-dong, TANG Sheng-jing (School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China) For the feature that the hypersonic vehicle shows serous nonlinearity, instability and parameter uncertainty when cruising at high altitude and great velocity, robust control method is proposed for the nonlinear system with normal load command included. By ignoring the height and constructing a virtual output signal from the integration of normal overload, the nonlinear system was fully linearized and input/output decoupling was achieved. The modified model was deduced and then a sliding mode tracking controller was designed. Simulation results indicate that the proposed control method can accurately track normal load commands. hypersonic vehicle; cruise flight control; feedback linearization; parameter uncertainty 2015-02-05; 2015-05-25; 时间:2015-06-24 15:03 赵林东(1986-),男,四川通江人,博士研究生,研究方向为高超声速飞行器建模与控制; 唐胜景(1959-),男,吉林九台人,教授,博士,主要从事飞行器设计和飞行力学研究。 V249.1 A 1002-0853(2015)06-0532-05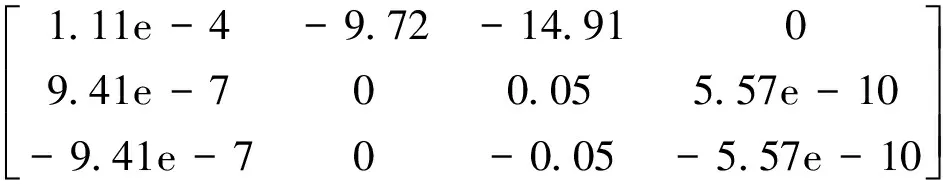
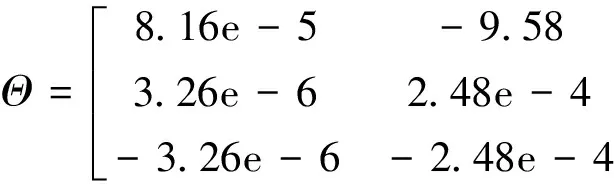

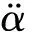


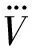
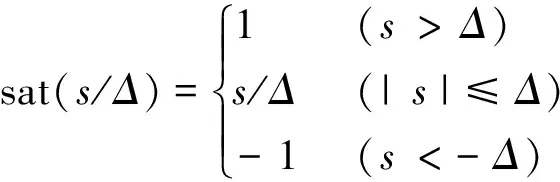
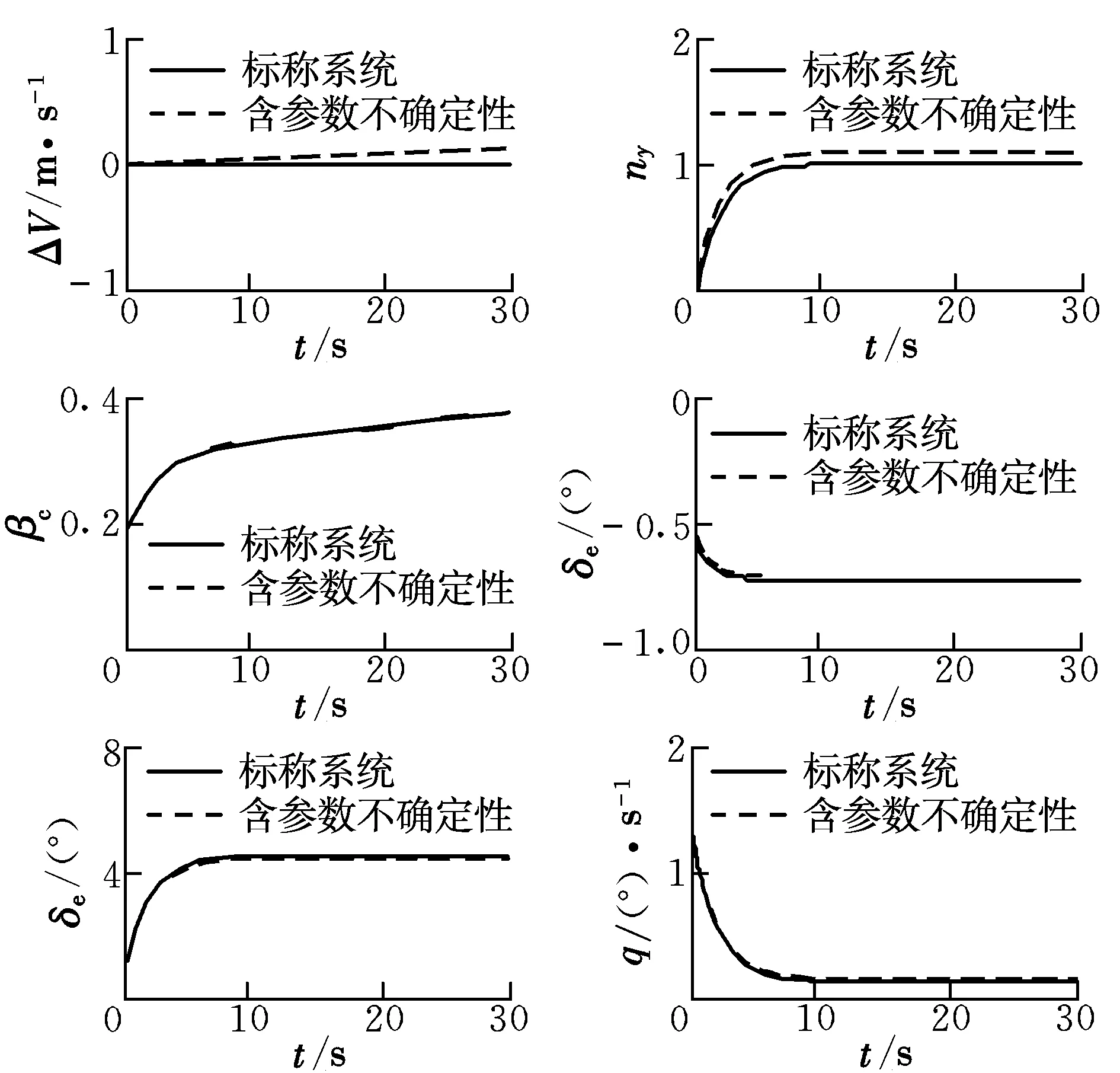
3 仿真与分析
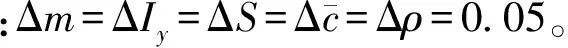
4 结束语
