非对称结冰条件下的飞机飞行动力学仿真

陈威, 徐浩军, 王小龙, 裴彬彬, 王健名

(空军工程大学 航空航天工程学院, 陕西 西安 710038)

非对称结冰条件下的飞机飞行动力学仿真

陈威, 徐浩军, 王小龙, 裴彬彬, 王健名

(空军工程大学 航空航天工程学院, 陕西 西安 710038)

飞机结冰是威胁飞行安全的重要因素之一,因此对结冰问题的研究显得尤为重要。基于非对称结冰模型,对飞机在结冰条件下的飞行动力学特性进行了仿真研究。提出了一种精确的结冰程度计算模型,建立了飞机非对称结冰模型,模拟了飞机在非对称结冰状态、不同结冰严重程度以及不同飞行阶段对结冰引起的滚转及偏航力矩的动态响应特性,并探讨了结冰对飞机飞行性能的影响。仿真结果表明,非对称结冰使飞机飞行性能恶化,而且飞机在非对称结冰状态下极易偏离正常飞行状态,对飞行安全造成巨大威胁。

非对称结冰; 不同飞行阶段; 不同结冰严重程度; 飞行动力学仿真

0 引言

结冰是飞机在结冰气象条件下飞行时,大气中的液态水在部件表面冻结并累积成冰的一种物理过程,是飞行中广泛存在的一种现象[1]。飞机结冰后不仅会改变飞机的气动外形而使飞行品质和飞行性能恶化,还会增加飞机的重量,脱落的冰层也经常会打坏飞机的机体结构或运动部件。目前,对于飞机结冰后的飞行动力学特性研究主要有计算模拟和试验研究两种方法[2]。由于试验研究风险大、费用高且周期长,因此大部分情况下还需要采用计算模拟的方法作为补充研究。国外在飞机结冰后飞行动力学仿真方面取得了不少突破性的进展,Bragg等[3]建立了一种飞机结冰参量模型,对飞机在结冰条件下的飞行动力学特性进行了研究;Lampton等[4-6]采用飞机结冰参量模型,基于小扰动理论研究了结冰对轻型飞机纵向及横航向的操纵响应特性。国内在这一领域起步相对较晚,周莉等[7]基于飞机本体非线性动力学模型，建立了不同状态的结冰模型,并计算了结冰前后飞机对驾驶员操纵的动态响应特性;张强等[8]提出了一种飞机结冰参量模型的参数计算方法,对飞机的结冰严重程度进行了评估,并分析了不同结冰严重程度对飞机造成的影响以及所应采取的对策。

上述工作主要针对飞机在对称结冰状态下的飞行动力学特性进行研究,而当某一侧机翼除冰设备发生故障时,机翼容易出现非对称结冰,此时飞机飞行动力学特性会发生较大改变。为了对非对称结冰状态下的飞行动力学特性有一个更全面的认识,本文在前人工作的基础上,建立了飞机非对称结冰模型,基于该模型模拟了飞机在非对称结冰状态、不同结冰严重程度以及不同飞行阶段对结冰引起的滚转及偏航力矩的动态响应特性,并探讨了不同严重程度结冰对飞机飞行性能的影响。

1 结冰程度计算模型

对于对称结冰状态下的飞机气动参数,利用以下模型进行计算[3]:

C(A)iced=(1+ηKCA)C(A)

(1)

式中:C(A)iced为结冰后该气动参数值;η为飞机结冰因子,只与气象条件有关,是不同气象条件下的结冰严重程度的反映;KCA为结冰系数,反映C(A)由于结冰所引起的变化量,对于给定的飞机KCA为常值;C(A)为结冰前飞机的某一气动参数。KCA的取值如表1所示[6]。

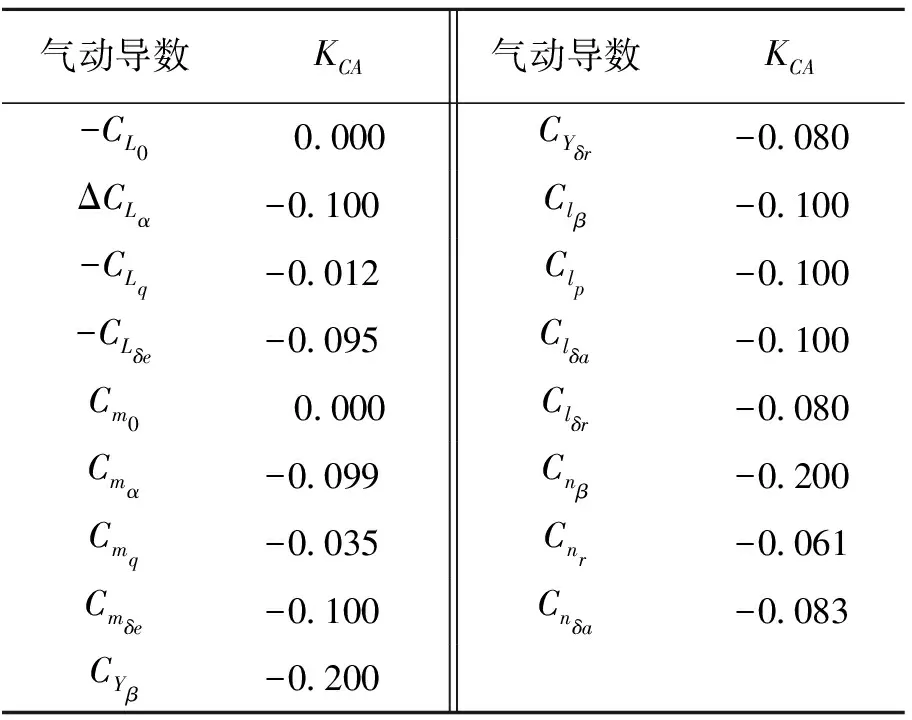
表1 飞机气动导数的结冰系数值Table 1 Icing factors of aerodynamic derivative

影响飞机结冰因子η的气象因素主要有三个:水滴直径(MVD)、液态水含量(LWC)及云层温度(T)。η与MVD,LWC及T的对应关系如下[3]:

η=f(E,n,Ac)

(2)

式中:E为收集效率;n为冻结系数;Ac为累积参数。其中:

E=mi/mp

(3)

式中:mi为参加撞击的水量;mp为机体投影面内的水量。

n=mf/mi

(4)

式中:mf为发生结冰的水量。

Ac=(LWC)V∞t/(ρc)

(5)

式中:V∞为来流速度;t为结冰时间;ρ为冰的密度;c为机翼弦长。

由式(2)可知,E,n,Ac决定着η的变化,而由式(3)～式(5)可知,E,n,Ac随结冰气象条件MVD,LWC,T改变,所以η与MVD,LWC,T之间存在直接对应的关系,设为η=g(MVD,LWC,T),把飞机结冰时的气象条件代入此关系的精确模型,就能得到飞机结冰严重程度的准确值。

2 结冰对飞机飞行性能影响的建模

在实际飞行过程中,机翼除冰系统总会存在一侧发生故障的可能,该侧机翼在结冰条件下极可能结冰,导致左右机翼升力及阻力改变,出现升力、阻力差,并由此产生滚转及偏航力矩。这种结冰情形与均匀结冰不同,因此,有必要针对不对称结冰单独构建模型。以下基于飞机六自由度全量微分方程组建立不对称结冰模型。

假设飞机在结冰条件下飞行时,右侧机翼的除冰系统出现故障不能正常除冰,则左右机翼产生升力差和阻力差,由此产生滚转力矩和偏航力矩。左右机翼的升力及阻力系数差值为[6]:

ΔCLice=(1/2)CLice-(1/2)CL

(6)

ΔCDice=(1/2)CD-(1/2)CDice

(7)

式中:CLice为结冰后的升力系数;CL为结冰前的升力系数;CDice为结冰后的阻力系数;CD为结冰前的阻力系数。

左右机翼产生升力及阻力差,导致滚转角加速度及偏航角加速度发生变化,变化量为[6]:

(8)

(9)

式中:d为沿体轴y由平均气动弦长到飞机中心线的距离。

将式(8)和式(9)代入飞机六自由度全量微分方程组,通过仿真计算,即可得到飞机在不同结冰严重程度以及不同飞行阶段的状态变化。

3 仿真计算结果及分析

以某型飞机为研究对象,利用本文所提出的不对称结冰模型,基于飞机六自由度全量微分方程组对飞机在不同飞行阶段和不同结冰严重程度下的滚转及偏航力矩响应特性进行仿真计算,并与结冰前进行对比分析。飞机结冰严重程度依次为η=0.3,0.5,0.7。根据联邦航空条例25部(FAR-25)附录C“大气结冰条件”,易结冰初始飞行条件设定为:H=5 500 m,V=150 m/s[9]。

为研究不同结冰严重程度以及不同飞行阶段对结冰引起的滚转及偏航力矩的动态响应特性,在仿真的过程中并没有加入驾驶员的修正操纵。

3.1 巡航状态下飞机不对称结冰

飞机初始状态为平飞状态，0 s出现不对称结冰，图1为巡航状态下飞机不对称结冰的动态响应曲线。

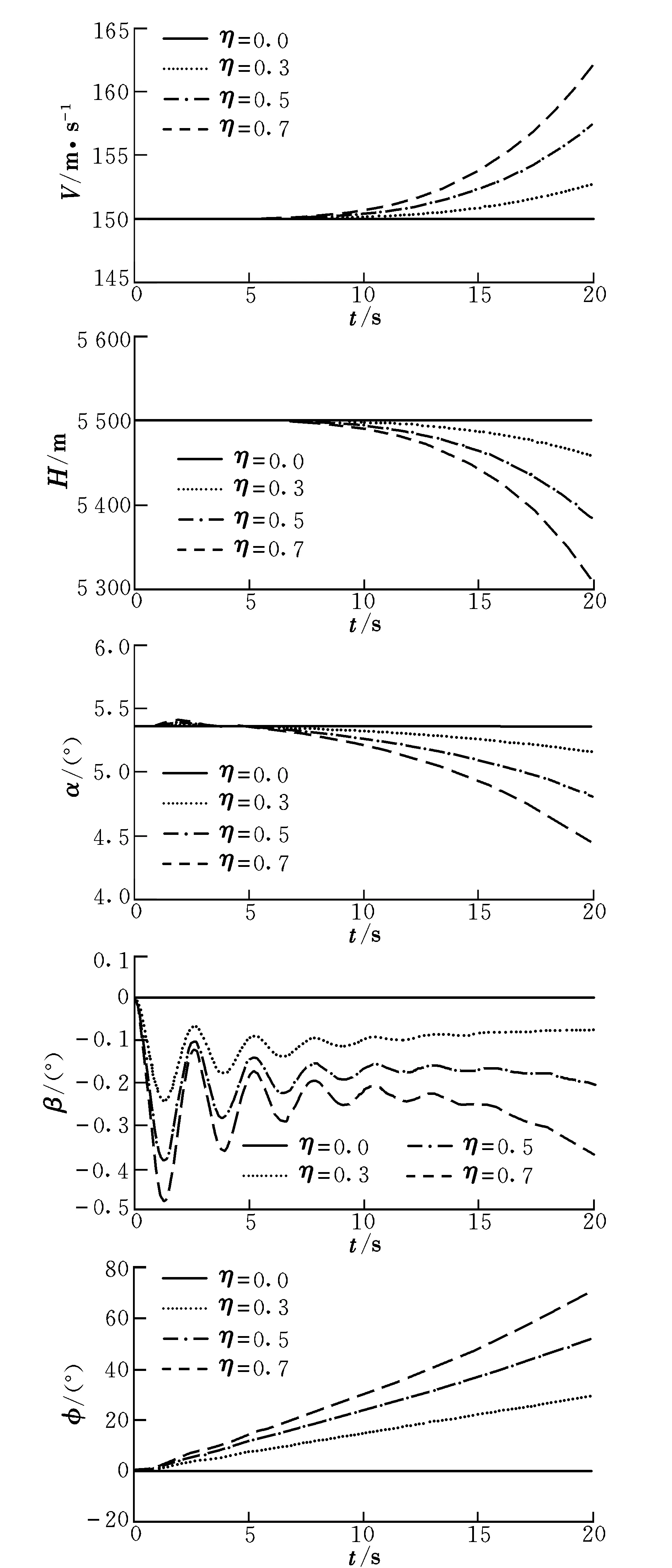
图1 巡航状态下的动态响应曲线Fig.1 Dynamic response curves of cruise stage

可以看出,未结冰飞机(η=0.0)始终处于平飞状态。随着η值的增大,高度损失增大。η=0.7时,H在20 s内下降了200 m,并且下降速率逐渐加快,由此导致速度也以逐渐增加的速率增大,可见结冰使飞机巡航性能下降。飞机的迎角逐渐减小,滚转角和侧滑角迅速改变,侧滑角的振荡幅度减小,并且振幅衰减较快;η=0.3时,φ在20 s已增大到30°,接近不允许坡度。

3.2 爬升状态下飞机不对称结冰

飞机初始状态为平飞状态,0 s出现不对称结冰,且0 s开始推油门进入爬升阶段,图2为爬升状态下飞机不对称结冰的动态响应曲线。

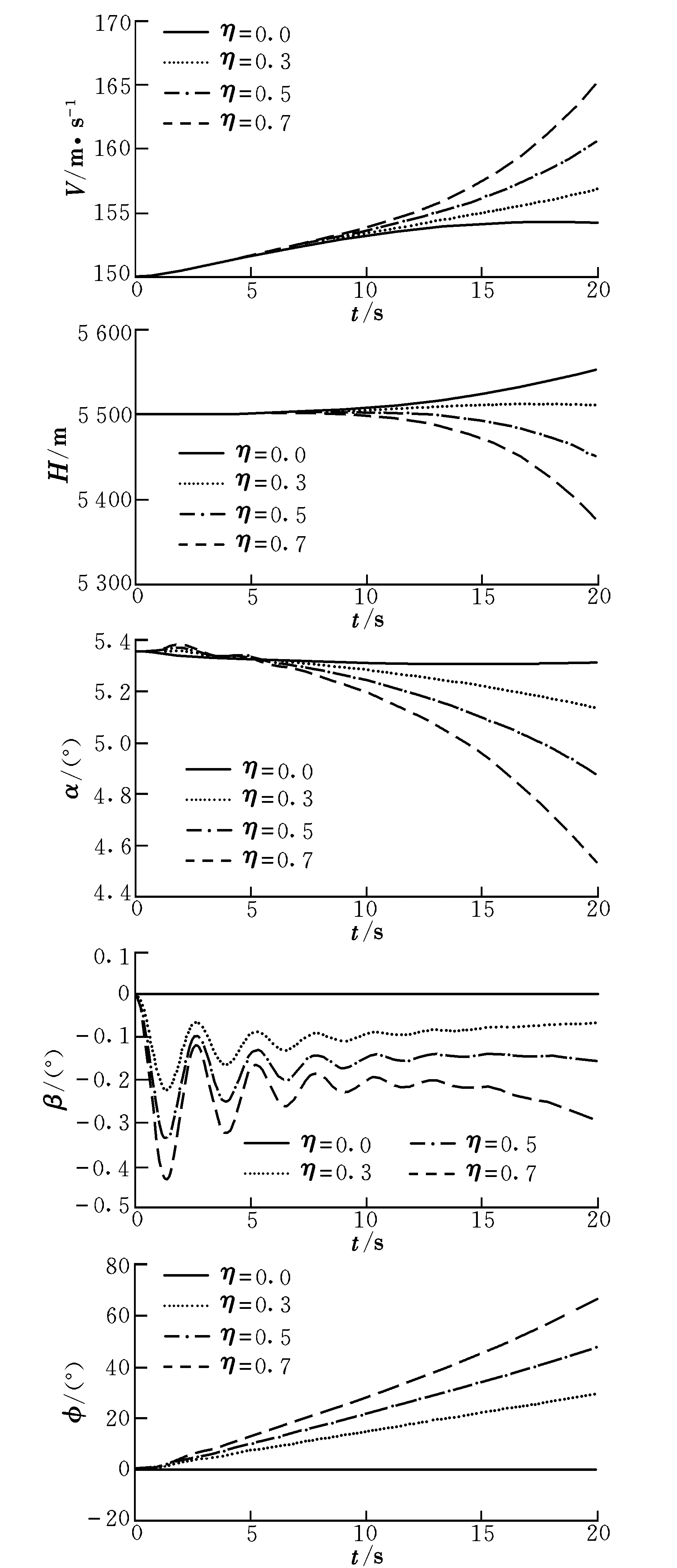
图2 爬升状态下的动态响应曲线Fig.2 Dynamic response curves of climb stage

可以看出,未结冰飞机飞行高度和飞行速度逐渐增加,爬升率Vyps=3 m/s;当η=0.3时,飞行速度比未结冰飞机变化大,H几乎保持在初始平飞高度,Vyps=0 m/s;当η>0.3时,H不升反降,并且下降高度和速率随着η的增大而增大,导致V也以逐渐增加的速率增大,可见结冰使飞机爬升性能下降。而通过与图1的比较可以发现,爬升状态下不对称结冰飞机的H,α,φ及β的变化规律以及数值与巡航状态下的几乎一致,这说明爬升操纵对不对称结冰飞机的飞行状态影响不大,起主要作用的是结冰不对称所导致的滚转力矩及偏航力矩。

3.3 下滑状态下飞机不对称结冰

飞机初始状态为平飞状态,0 s出现了不对称结冰,且0 s开始收油门进入下滑阶段,图3为下滑状态下飞机不对称结冰的动态响应曲线。

由图3可以看出,未结冰飞机在平稳地下滑,下滑率Vyxh=-2 m/s;当飞机出现不对称结冰后,H在前10 s内与未结冰飞机几乎一致,在10 s 后急剧下降,并且变化量随η的增大而增大,导致Vyxh逐渐增大,V在前10 s内平稳减小,而在10 s后以逐渐增加的速率增大,可见结冰使飞机的下滑性能下降。此外,通过与图1的比较可以发现,出现不对称结冰后,下滑状态下的H,α,φ及β与巡航状态下的数值很接近,这同样也说明下滑操纵对飞机飞行状态的影响不大,起主导作用的是结冰不对称所导致的滚转力矩及偏航力矩。

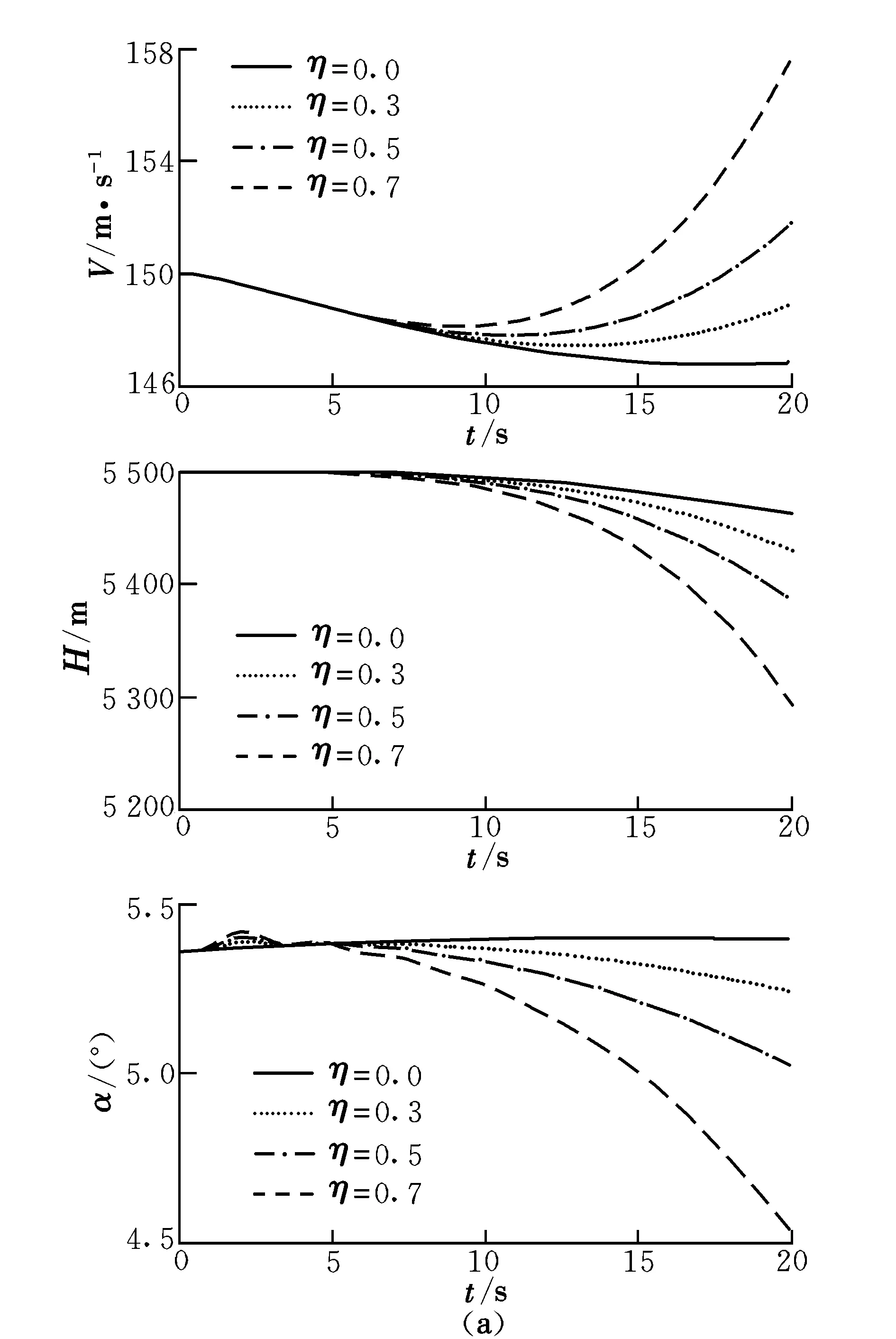
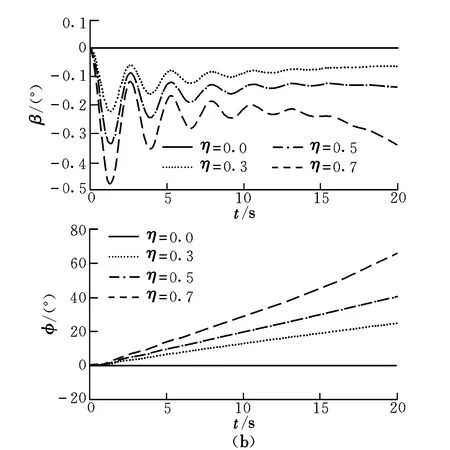
图3 下滑状态下的动态响应曲线Fig.3 Dynamic response curves of descent stage

综合以上仿真结果可以看出,不对称结冰的影响随着η的增大而增强,导致飞机飞行性能下降,并且对飞行状态起主要作用的是结冰不对称所导致的滚转力矩及偏航力矩。当η<0.3时,不对称结冰的影响很明显,但尚在可控范围之内;当η>0.3时,φ迅速改变,飞机严重偏离正常飞行状态,对飞行安全造成巨大威胁。因此,在飞行过程中应当尽量避免不对称结冰情况的出现。

4 结论

本文通过建立非对称结冰模型,并基于该模型对飞机在不同结冰严重程度以及不同飞行阶段的飞行动力学特性进行了仿真研究,得出以下结论:

(1)不对称结冰使飞机的爬升、巡航以及下滑性能恶化,爬升操纵和下滑操纵对飞行状态的影响不大,起主要作用的是结冰不对称所导致的滚转力矩及偏航力矩。

(2)不对称结冰的影响随η的增大而加剧,当η较大时,飞机极易进入失控状态,尤其是滚转失控,对飞行安全造成巨大威胁。对此,驾驶员应当高度重视并采取适当的策略来修复。

[1] Cole J,Stands W.Statistical study of aircraft icing accidents[R].AIAA-91-0538,1991.

[2] 朱东宇.翼型结冰过程的数值模拟[D].南京:南京航空航天大学,2009.

[3] Bragg M B,Hutchison T,Merret J,et al.Effect of ice accretion on aircraft flight dynamics[R].AIAA-2000-0360,2000.

[4] Lampton A,Valasek J.Prediction of icing effects on the lateral/directional stability and control light airplanes[R].AIAA-2006-6487,2006.

[5] Lampton A,Valasek J.Predicition of icing effects on the dynamical response of light airplanes[J].Journal of Guidance,Control,and Dynamics,2007,30(3):722-732.

[6] Lampton A,Valasek J.Prediction of icing effects on the coupled dynamic response of light airplanes[J].Journal of Guidance,Control,and Dynamics,2008,31(3):656-673.

[7] 周莉,徐浩军,闵桂龙,等.结冰对飞机动态响应特性的影响[J].飞行力学,2011,29(4):32-36.

[8] 张强,刘艳,高正红.结冰条件下的飞机飞行动力学仿真[J].飞行力学,2011,29(3):4-7.

[9] Federal Aviation Administration.Code of federal regulations,title 14,chapter 1,subchapter c—aircraft:part 25—airworthiness standards:transport category airplanes[S].US:Federal Register,1990.

(编辑：姚妙慧)

Aircraft flight dynamics simulation under asymmetric ice accretion

CHEN Wei, XU Hao-jun, WANG Xiao-long, PEI Bin-bin, WANG Jian-ming

(Aeronautics and Astronautics Engineering College, AFEU, Xi’an 710038, China)

As the in-flight icing could cause great threat to flight safety, the research on ice accretion is of significance. The asymmetric icing effect model is proposed to simulate the flight dynamics under icing conditions. Together with an exact icing severity calculation model, the asymmetric icing effect model is adopted to study the dynamic response characteristics to rolling and yawing moment, which is caused by asymmetric icing under different icing severities and flight stages. Moreover, the influence of icing on aircraft flight performance is also analyzed. The results of simulation show that asymmetric icing could decrease aircraft flight performance and make the aircraft deviate from steady flight state, which would bring great threat to flight safety.

asymmetric icing; different flight stages; different icing severity; flight dynamics simulation

2015-04-10;

2015-08-05;

时间:2015-08-17 11:04

国家自然科学基金资助(61374145);国家重点基础研究发展计划基金资助(2015CB755802)

陈威(1992-),男,湖北黄冈人,硕士研究生,研究方向为飞行仿真与飞行安全; 徐浩军(1965-),男,浙江余姚人,教授,博士生导师,研究方向为飞行安全及等离子体隐身。

V212.1

A

1002-0853(2015)06-0491-04