一种用于FTPVS数据处理的非平稳度定义

谭博, 郑华, 裴承鸣

(西北工业大学 动力与能源学院, 陕西 西安 710072)

一种用于FTPVS数据处理的非平稳度定义

谭博, 郑华, 裴承鸣

(西北工业大学 动力与能源学院, 陕西 西安 710072)

为解决非平稳程度量化问题及优化非平稳信号处理方法的精度,针对试验数据特点,提出了一种基于时频分析的非平稳度定义方法,使得处理方法的各项参数能够随非平稳度变化进行实时调整,从而提高数据处理结果的精度。通过仿真试验,对非平稳度定义的合理性和实用性进行了研究,并通过风洞试验及飞行试验的数据处理证实了其工程实用性及对非平稳数据处理方法精度的影响。试验结果表明,所提出的非平稳度不仅可以可信地表征信号非平稳程度,而且还可以辅助提高FTPVS数据处理结果的精度。

非平稳度; 替代数据; FTPVS

0 引言

在传统的台阶式颤振试验中,往往要求试验的各项参数在达到指定水平后保持一段时间,以完成试验信号的采集工作,以此保证采集信号的分段平稳性,使得传统的平稳信号分析方法可以用于后续处理工作,但也因此产生了诸如周期长、成本高、不符合真实飞行器的飞行状态且在临界速度附近的安全性较差等不足。为了克服这些缺点,近年来出现了一类连续变速的颤振试验(FTPVS)方法。在这类试验中,各项参数不断变化,数据采集工作同步进行,通过对信号的实时处理以研究试验对象的当前状态。对这类试验而言,其采集信号多为非平稳随机过程,这类信号处理结果的性能会受到信号非平稳程度的影响。当非平稳程度低时,甚至可以采用平稳信号处理方法进行分析;而当非平稳程度高时,若不能及时对处理方法做出相应调整,将会很难取得理想的结果, 为分析处理带来难度。这使得针对非平稳程度的量化工作变得十分必要[1-3]。

至于非平稳度的定义及计算方法,由于非平稳信号在各个领域内有不同的特点,目前尚未有明确统一的标准,现有的几种定义多为针对特定应用领域内的实际问题而提出,往往只适用于一类或几类信号,不能用于解决其他领域内的问题,因此无法用于FTPVS信号非平稳度的量化。而对于这类试验信号而言,其显著特点为能量分布随时间会发生变化,在试验临界状态下这一变化会明显加剧。由此认为，通过对能量分布变化剧烈程度的描述,可以得到这类信号的非平稳度。针对这一特点,本文提出了一种基于时频分布的非平稳度定义及计算方法,随后通过仿真数据及试验数据对定义的合理性及工程实用性进行了研究,最后结合工程试验,研究了其对改善非平稳信号处理方法精度的影响。结果表明,本文定义的非平稳度对能量分布变化具有良好的线性响应,能够可信地表示出信号能量分布变化的剧烈情况,依据此非平稳度调整处理方法的参数可以取得更加理想的分析结果。

1 FTPVS信号特点

对于试验中的采集信号而言,可以通过时频表示的方法将频谱随时间变化的一维时域信号x(t)或频域信号X(ω)映射成为时间-频率平面上的二维信号Sx(t,ω),以Hermite函数作为窗函数的时频分布为例,得到信号x(t)的Hermite窗函数时频分布如下:

式中:hk(t)为k阶Hermite函数。

对于传统颤振试验而言,通常认为其采集信号为分段平稳信号。在每一段采集时间内，信号能量分布不会随时间发生变化,因此其在任意时间点的局部能量分布应等于其全局能量分布的均值,即:

式中:〈·〉表示分布的期望。

对于FTPVS试验而言,由于在试验过程中各项因素不断变化,其能量分布Sx,K(t,f)在采集时间内也不停地变化,这一变化在接近临界状态时的幅度会大幅加剧。此时其局部能量分布与全局能量分布之间不再存在上式中的关系,为了刻画局部能量分布变化的剧烈程度,提出了一种基于时频分布的非平稳度定义及计算方式。

2 非平稳度定义

借助Theiler等[4]提出的替代数据法,可以得到原始信号的具有平稳性质的替代数据,这些替代数据具有与原始信号相同的幅频特性,且保持了其二阶统计矩不变。依据第1节的讨论可知,替代数据局部时频分布应与全局时频分布的均值相等。而对于原始信号,其局部时频分布应为一个彼此不同的分布集合,{S(t1,f),S(t2,f), …,S(tn,f)},计算这个集合的方差,就可以得到一个表征原始信号x(t)频域能量分布随时间变化的“起伏”程度的量θ1[5]:

θ1=E(cn-E(c)) (n=1,…,N)

其中:

cn=D(S(tn,f),〈S(tn,f)〉n)

式中:D(…)为两个分布之间距离的计算方法。为了灵敏地反映信号的幅度以及频率变化,这里选用Basseville[6]给出的距离定义。

由平稳信号的特点可知,在理想的条件下替代数据的θ值应为零,但实际应用中,由于采用相位的随机性,θ值往往会分散在一个相对较小的范围内,将该范围记为平稳过程的θ值区间。对多个替代数据的θj值进行分布统计并设置阈值,给出非平稳度的定义为:

式中:θ1为原始信号的θ值;θ0为替代数据θ值得到的平稳区间的阈值。易知信号的DNS值恒为正且无上限,平稳信号的DNS值小于或等于1,而非平稳信号的DNS值则大于1。

3 仿真试验验证

为了对定义DNS的合理性进行验证,参考文献[7-8],通过为一个频率为2 Hz、采样率为128、采样长度为128的正弦信号引入幅值系数和常系数来考察二者对信号DNS的影响,最终计算得到的DNS结果如表1所示。二者的计算公式如下:

x(t)′=kC+kAx(t)

上述的三类传统算法主要基于图像整体信息的变化来选定关键帧，容易造成关键帧选取错误、计算量大、实时性差等问题。因此，本文在此基础上使用一种基于深度学习的目标检测方法，通过建立卷积神经网络(Convolutional Neural Network，CNN)模型，分类提取视频中列车头部、尾部及车身所在关键帧，使得基于深度学习的目标检测在关键帧提取的应用中成为可能。

式中:kC为常系数;kA为幅值系数。

表1 不同幅值系数及常系数下DNS的值Table 1 DNS of signals with different parameters

由计算结果可以看到,由于本文定义的DNS表征的是信号能量分布随时间变化的快慢程度,而幅值系数不会改变信号能量分布变化,所以它对信号的DNS值没有影响;但是常数系数的加入相当于为信号添加了低频的趋势信号,会影响信号的能量分布,因此计算得到的DNS值有小幅度波动,但是总体而言,仍处于前文讨论的平稳信号DNS范围内。

为了考察所定义的DNS对信号非平稳程度表示的可信度,利用仿真生成变幅和变频两类正弦信号以观察DNS值随频率或幅值变化速率的改变情况。由前文可知,为信号引入整体幅值系数不影响信号DNS值,因此对幅值变化速率的考量以幅值变化倍率的速度为自变量,而对频率变化则包括起始频率和终止频率两个方面。所生成仿真信号采样率为128,采样长度为1 024。最终得到对应DNS值的结果如图1和图2所示。

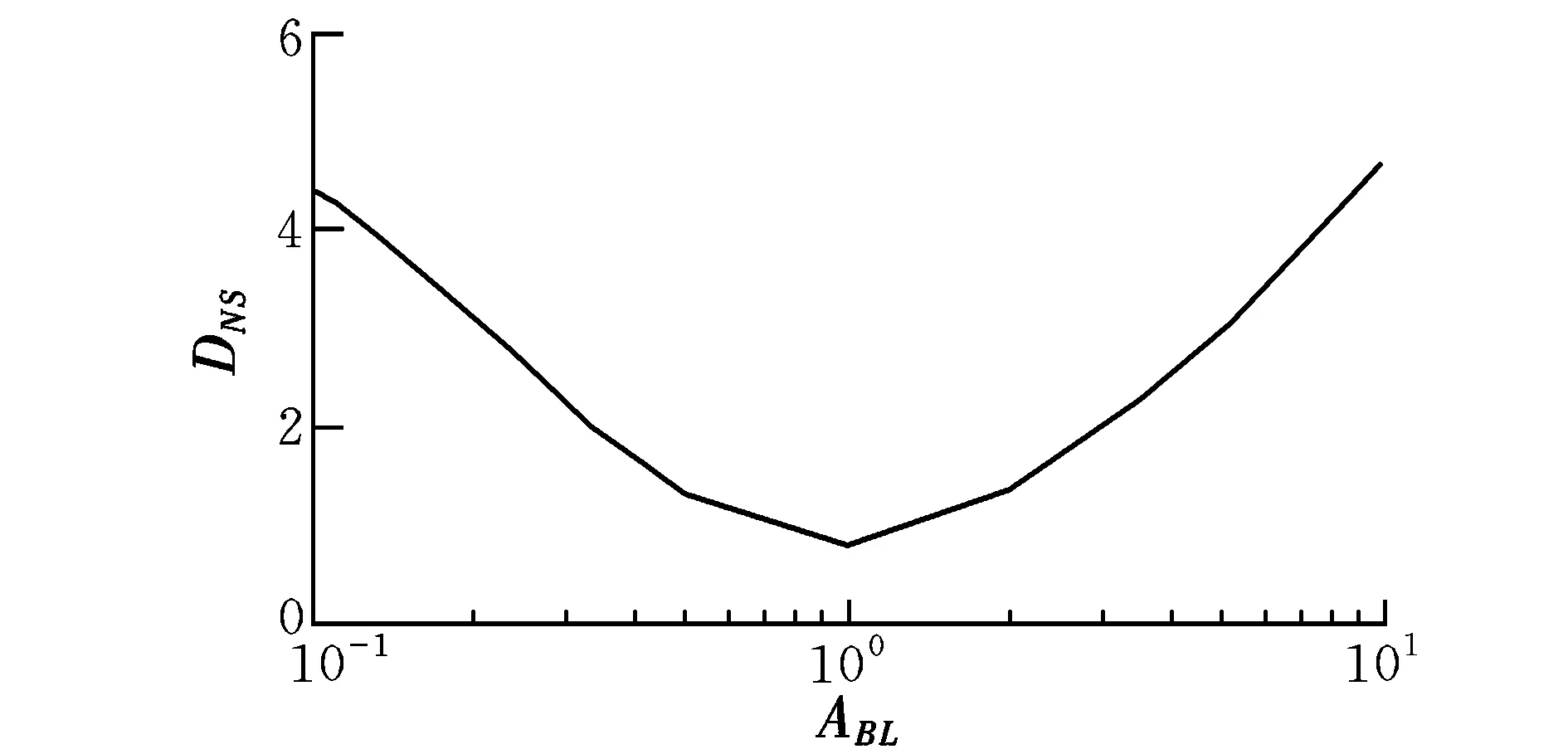
图1 变幅信号DNS值计算结果Fig.1 DNS of variable amplitude signals

图2 变频信号DNS值计算结果Fig.2 DNS of variable frequency signals

图1中,x轴为信号幅度变化的倍率ABL,曲线的最低点对应平稳信号的DNS值,位于最低点左侧的各点对应信号幅值随时间减小的信号对应的DNS值,DNS最大值对应的信号其幅值在终止时刻为初始时刻的0.1倍;位于最低点右侧的各点表示信号幅值随时间增大时的DNS值,最大值对应的信号幅值在终止时刻为初始时刻的10倍,曲线两侧均近似线性且较为对称。这一现象表明,信号幅值产生等倍率的缩小或增大时对应的DNS值一致,且与DNS值近似呈现正比关系。在图2中,x轴为扫频信号初始时刻的频率f0,y轴为扫频信号终止时刻的频率ff,z轴为信号DNS值。由图中可以看到,在起始频率和终止频率相等的xy平面对角线上的DNS值相对最小,这是因为这些DNS值为不同频率正弦信号的计算结果。DNS值在平面两侧逐渐上升,且表现出较好的线性与对称特性,这表明DNS值仅与频率变化速率相关,具有较好的指示意义。

4 颤振试验验证

FTPVS是一类新兴的飞行器颤振试验方法,与传统的试验方法相比,其根本区别在于其采集数据非平稳,这使得传统的颤振数据处理方法难以应用。由于非平稳数据处理方法的数值性能很大程度上受到观测信号非平稳程度的影响,因此,对被测信号的非平稳度进行测量变得十分必要。下面以实际的风洞试验及飞行试验数据为例,验证本文方法在实际试验数据处理中的应用效果。

4.1 颤振风洞试验

某次风洞试验的观测通道试验数据及对应的风速随时间的变化趋势如图3和图4所示,被测信号DNS值变化如图5所示。

图3 风洞试验实测信号Fig.3 Measured signal in wind tunnel test

图5 信号的DNS值Fig.5 DNS of signal

4.2 颤振飞行试验

本次试验数据来自某型飞机跨声速颤振飞行试验[9]。所选用数据中包含了跨声速阶段的采集数据,采集数据如图6所示。对飞行高度和飞行速度进行归一化处理后,得到的随时间变化情况如图7所示。计算被测信号每一秒的DNS值,得到其随时间的变化如图8所示。

图6 飞行试验实测信号Fig.6 Measured signals of flight test

图7 飞行参数Fig.7 Flight parameters

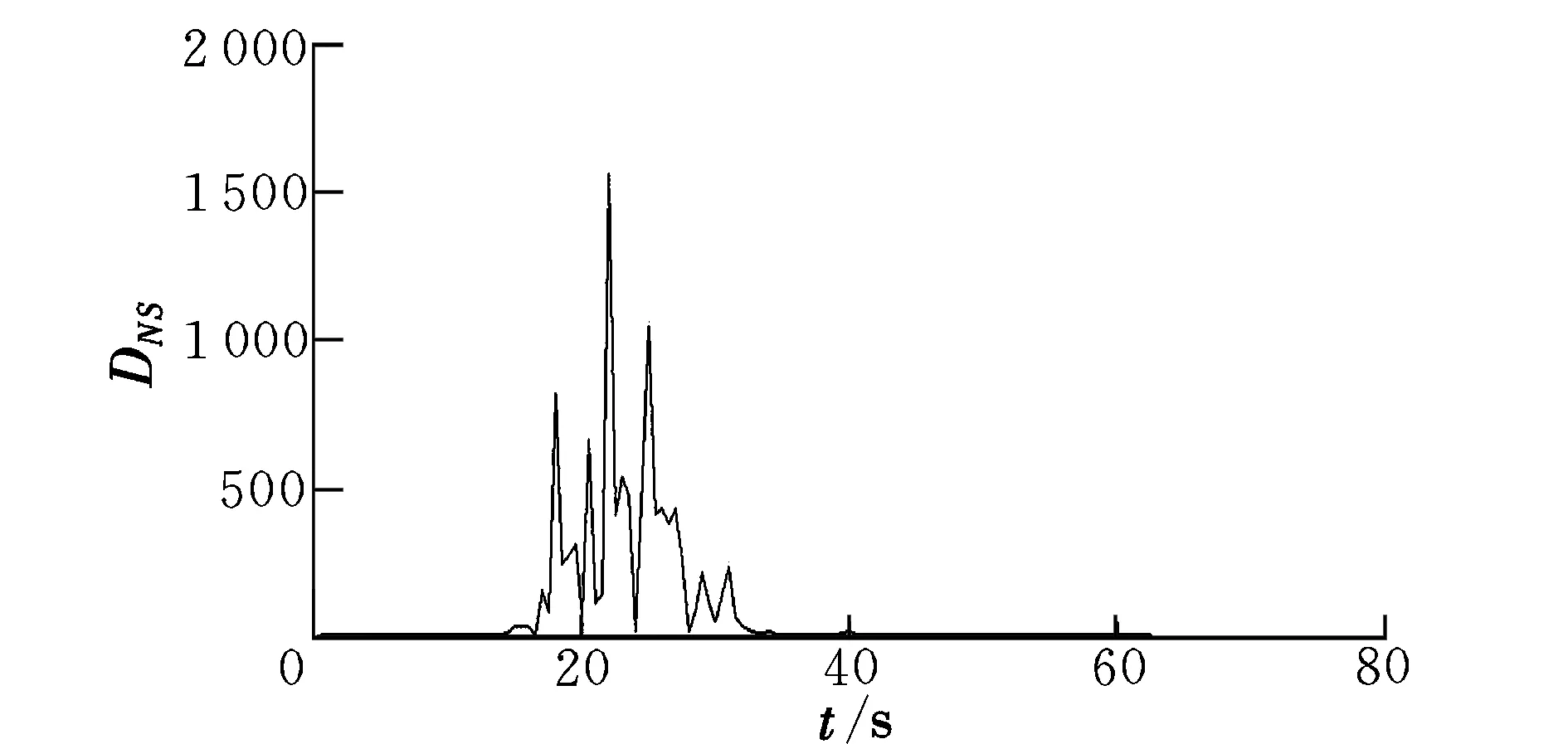
图8 信号的DNS值Fig.8 DNS of signal

与风洞试验相比,飞行实测信号受到的影响更多,因此信号的DNS变化也更加多样。由图7可以看到,在19～30 s时间段内,飞行器的高度表读数及速度表读数同时发生了跳变,这段时间正对应飞行器突破音障的时间,飞行器受到外部条件的影响,其固有模态发生了变化,致使信号能量分布在短时间内大幅变动。由图8可以看到,信号的DNS值在19～30 s时间段发生了突变,而突破音障后这一影响便不再存在,信号的DNS值再次回落至较低水平,这说明本文DNS定义对结构模态的改变十分敏感,也证实了本文方法的有效性。

4.3 非平稳度在FTPVS数据处理中的应用

在4.1节和4.2节的试验数据分析中,可以看出本文定义的非平稳度可以客观地反映出监测信号的非平稳程度变化,从而为判断测试对象的当前状态提供可靠的依据。同时,应用信号非平稳度还可以提高数据处理方法的精度。下面参考文献[10]，以非平稳信号处理中,常见的应用粒子滤波建立系统的时变自适应模型方法为例,说明如何应用非平稳度提高建立模型的精度。

选用4.1节中的风洞试验信号作为分析对象。首先采用粒子数设为100的一般粒子滤波方法建立被测对象的四阶系统模型，所得模型输出与实际采集信号的相对误差δ如图9所示。

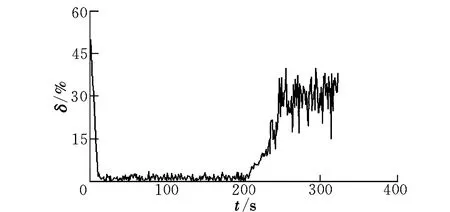
图9 一般粒子滤波结果相对误差Fig.9 Relative error of traditional particle filtering results

由图9可见,在信号非平稳度低的时段(0～200 s),采用一般粒子滤波方法经过短时间的自适应调整,就可建立相对误差较小的系统模型;而在非平稳度上升的时段中(200～290 s),随着信号的非平稳度上升,相对误差逐渐增加,直至试验结束时仍存在较大的相对误差。此时应用传统的方法已经难以建立对象的精确系统模型。接下来利用信号的非平稳度对粒子滤波方法中的粒子数目进行调整,其数目变化与非平稳度变化曲线一致,图10为调整后得到的模型输出与实际采集信号的相对误差。

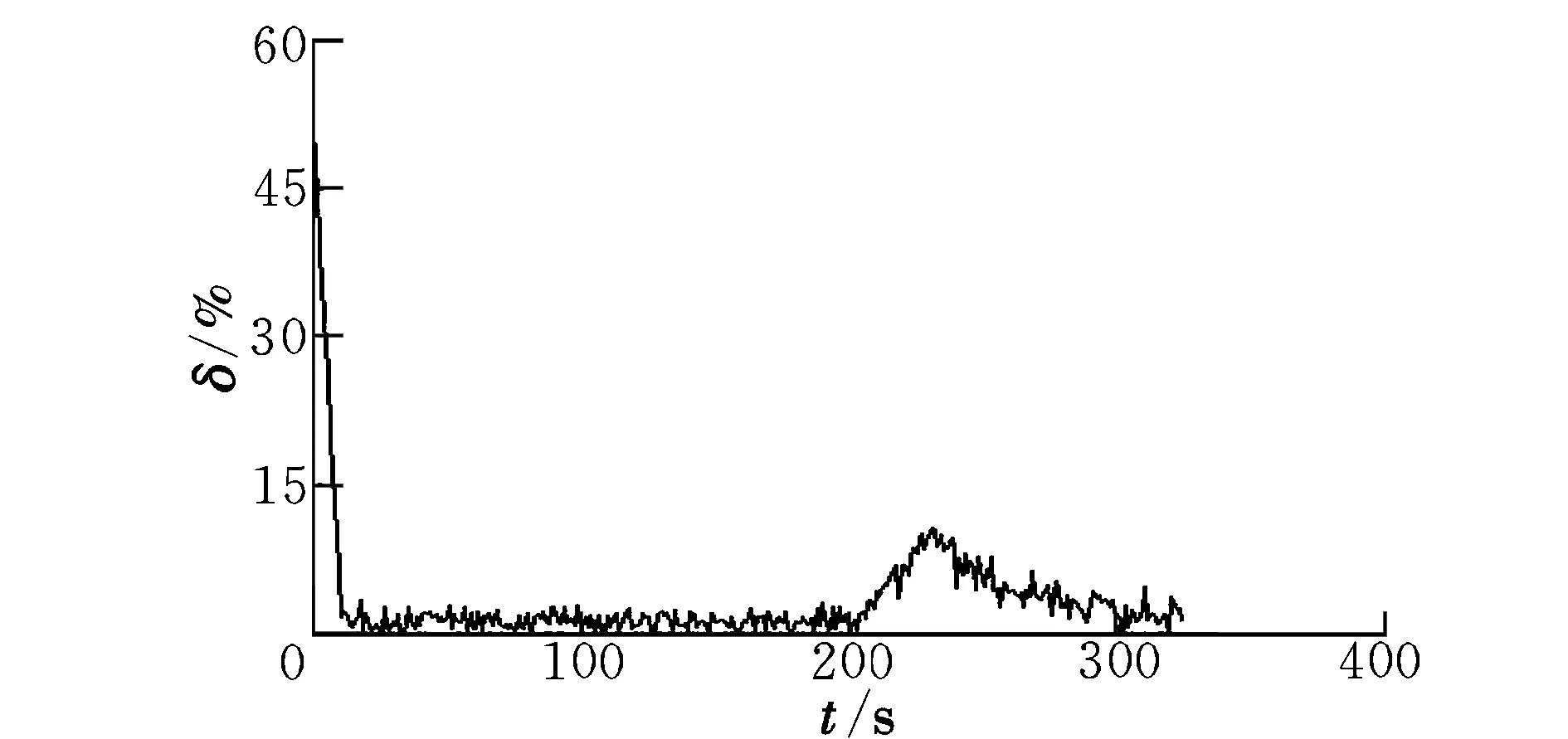
图10 调整参数后粒子滤波结果Fig.10 Particle filtering results after parameter adjustment

由图10可见,当信号非平稳度上升时,由于粒子数目也随之调整,因此在相对误差达到一定程度后开始逐渐减小,至试验结束时,这一误差已经减小至一个可以接受的范围内。由此可见,依据非平稳度调节算法，可以在很大程度上提高相关参数分析结果的精度,具有良好的工程应用前景。

5 结束语

本文借助替代数据生成方法,给出了一种适用于FTPVS数据处理的非平稳度的定义及计算方法。仿真结果证实了其对于信号的非平稳性具有良好的分辨能力,且对于非平稳度的变化具有较强的指示能力。通过对实际连续变速风洞试验以及飞行试验数据的非平稳度进行计算,验证了这一定义在实际数据处理的应用中,可以明确地反映出被测信号能量的变化,从而反映出试验对象结构模态的变化,具有较强的理论研究价值和潜在的工程应用前景。

[1] 王宏禹,邱天爽,陈喆.非平稳随机信号分析与处理[M].北京:国防工业出版社,2008:1-52.

[2] 向馗,蒋静坪.时间序列的非平稳度分析[J].科技通报,2007,23(1):1-5.

[3] 张海勇.基于局域波法的非平稳随机信号分析中若干问题的研究[D].大连: 大连理工大学,2001.

[4] Theiler J,Eubank S,Longtin A.Testing for nonlinearity in time series:the method of surrogate data[J].Physica D,1992,58(1):77-94.

[5] Borgnat P,Flandrin P,Honeine P,et al.Testing stationarity with surrogates:a time-frequency approach[J].IEEE,Transactions on Signal Processing,2010,58(7):3459-3470.

[6] Basseville M.Distances measures for signal processing and pattern recognition[J].Signal Process,1989,18(4):349-369.

[7] 赵善红.颤振边界预测的时频共振方法研究[D].西安:西北工业大学,2002.

[8] 张文,刘玉田.自适应粒子群优化算法及其在无功优化中的应用[J].电网技术,2006,30(8):19-24.

[9] 陈志敏,薄煜明,吴盘龙.基于自适应粒子群优化的新型粒子滤波在目标跟踪中的应用[J].控制与决策,2013,28(2):193-200.

[10] 郑华,谭博,裴承鸣.粒子滤波算法在多传感器测量中的应用[J].现代电子技术,2014,37(1):24-26,30.

(编辑：姚妙慧)

A methodology of non-stationary degree suitable for FTPVS data processing

TAN Bo, ZHENG Hua, PEI Cheng-ming

(School of Power and Energy, NWPU, Xi’an 710072, China)

Aiming at qualifying of non-stationary and better analysis results, a methodology of non-stationary degree based on time-frequency analysis is proposed in this paper according to the characteristics of actual collected data, which makes it possible to modify the related parameters of processing method according to non-stationary degree. Non-stationary degree proposed in this paper is tested through both simulation data and actual experimental data. The results show the non-stationary degree in this paper could credibly indicate the non-stationary degree and could be used to improve the accuracy of processing methods for FTPVS.

non-stationary degree; surrogate data; FTPVS

2015-03-05;

2015-06-02;

时间:2015-08-17 11:04

国家自然科学基金资助(11302175)

谭博(1987-)，男，陕西西安人，博士研究生，主要研究领域为时变参数建模、非平稳信号处理； 郑华(1983-)，男，河南南阳人，讲师，主要研究领域为自适应控制算法、非平稳信号处理。

V215.34

A

1002-0853(2015)06-0560-05