多跑道飞机降落排序快速优化方法
2015-03-15张勰刘宏志赵嶷飞
张勰, 刘宏志, 赵嶷飞
(中国民航大学 天津市空管运行规划与安全重点实验室, 天津 300300)
多跑道飞机降落排序快速优化方法
张勰, 刘宏志, 赵嶷飞
(中国民航大学 天津市空管运行规划与安全重点实验室, 天津 300300)
针对多跑道飞机降落排序这一典型的组合优化问题,建立了以延误代价最小为目标的优化模型,并提出了一种基于贪心策略的动态规划算法。在生成子节点时引入贪心策略,通过简化搜索过程的复杂度,提高算法运行效率,以解决问题规模增大导致计算效率低下的难题。仿真结果表明,该方法能够有效简化搜索过程,在优化效果与动态规划算法相当的情况下,有效降低了运算时间,证明了方法的有效性。
空中交通管理; 降落排序; 多跑道; 贪心策略
0 引言
飞机降落排序是终端区空中交通的一个重要环节,顺畅、高效的排序方案有助于缓解终端区空中交通拥堵,减少飞机空中延误,进而提高整个空管系统的运行效率,对于实现空中交通管制现代化、自动化具有重要的现实意义。
飞机降落排序需要确定飞机的降落顺序、降落跑道和降落时间,是一个NP-hard问题[1]。考虑跑道调度和着陆时间的制定,该问题的解空间十分庞大,而且对各种参数(如时间、飞机数目、跑道数目等)十分敏感[2-3]。传统方法在问题规模不大时能够有条件地求得有效解,在问题规模逐渐增大的情况下,由于计算代价过大,难以在理想时间范围内找到优化解[4-6],导致这些算法的应用受到极大的限制。本文针对多跑道降落排序问题,提出了基于贪心策略的快速优化方法,该方法大大降低了搜索过程的复杂度,使得优化排序方案兼顾了实时性与可行性。
1 问题模型
跑道数量、构型与实际运行模式都会影响飞机排序方案,考虑到目前我国多跑道机场多为平行双跑道配置的现实情况,本文以平行双跑道为例进行讨论。
考虑一平行双跑道机场,已知待降落飞机队列中各飞机的初始预计降落时间与时间窗,在满足一定约束条件的情况下,对各飞机的降落顺序、降落跑道、降落时间进行优化。
1.1 优化目标
延误代价是飞机排序问题中的首要考量要素,于是有:
(1)
式中:F为飞机集合;延误时间tDTi=tSTAi-tETAi,tDTi>0表示飞机i发生了延误,tDTi=0表示飞机i正点到达,tDTi<0表示飞机i提前到达;tSTAi和tETAi分别为飞机i的优化降落时间和预计降落时间;αi和βi分别为延误代价系数和提前代价系数;C为单位时间的延误成本。
1.2 约束条件
1.2.1 降落顺序约束
(2)
式中:λij为飞机i与j之间的降落顺序,λij=1表示飞机i早于j降落,λij=0表示飞机i晚于j降落;λij+λji=1,i≠j。
1.2.2 安全间隔约束
tSTAj-tSTAi≥Sij(i≠j)
(3)
本约束表明,若飞机i早于j降落,则它们之间的间隔必须大于两者之间的最小安全间隔Sij。
国际民航组织规定:根据飞机的最大起飞重量,飞机可以分为重型机H、中型机M、轻型机L三种类型。终端区内待排序飞机队列是由不同类型的飞机组成的,飞机的前后顺序不同所需要的最小尾流间隔也不同。国际民航组织对不同类型飞机间的最小尾流间隔(单位为m)的规定如表1所示。
1.2.3 降落顺序约束
本文采用的多跑道模型为两条平行跑道的模型,并处于相关运行模式下,这是实际中较为常见的一种双跑道配置模式,在我国具有较为普遍的代表性。多跑道调度除了需要给飞机分配降落时刻和顺序外,还要指定其降落的跑道,且相邻飞机在不同的跑道上降落也需要保证一定的安全时间间隔。在相关运行模式下,两条跑道可以一先一后安排飞机着陆,前后飞机之间的侧向间距为不小于4 km,此侧向间距可以转化为40 s的着陆时间间隔,而这一时间间隔与飞机类型无关。也就是说,对于在同一跑道上降落的两架飞机之间必须按其机型配备满足表1所示的安全间隔要求,而对于在不同跑道降落的两架飞机之间只需保证40 s的间隔即可。于是有:
(4)
式中:Zij=1表示飞机i与飞机j在同一跑道降落;Zij=0表示在不同跑道降落。
1.2.4 位置交换约束[7]
考虑到管制员的工作负荷和运行安全,降落调度中过大的位置调整在管制运行中是不实际的,即调度前后飞机位置的变动幅度不能超过一定的范围。例如最大位置偏移量为2,若某架飞机在先到先服务的队列中排在第5位,则它在新队列中只能占据第3,4,5,6,7位。这种思想不仅保证了一定的公平性,还极大地缩小了解空间。
设k为最大位置偏移量,飞机i在初始队列中的位置为Ai,在新队列中的位置为A*i,则:
(5)
1.2.5 降落时间窗
受飞机性能和进场程序等条件的限制,飞机只能在特定的降落时间窗内降落在跑道上,如式(6)所示:
tSTAi∈[tETAi-tAmax,tETAi+tDmax]
(6)
此外,飞机在终端区内可以通过一定时间的盘旋飞行来吸收延误,因此飞机的降落时间窗就扩展为若干段离散的时间段,如式(7)所示:
tSTAi∈[tETAi-tAmax,tETAi+tDmax]+NTh
(7)
式中:N为盘旋圈数;Th为盘旋一圈所需的时间。
2 基于贪心策略的排序算法
2.1 动态规划算法
文献[8]提出了一种求解飞机排序问题的动态规划算法,其基本思想为:按降落飞机架数0到n递推,递推到m架时,需要计算、存储满足条件的所有情况,即降落的所有m架飞机及其可能的所有排列方式。受位置交换约束中k值的影响,可以知道当前m架飞机中已确定降落顺序的为第1~m-k架,而第m-k+1~m架的k架飞机则尚未确定降落顺序,且这k架只可能为原序列第m-k+1~m+k飞机中的任意k架[8]。所以可以用这k架飞机为第m层的飞机节点编号:每个节点存储一定的飞机降落时间信息,即可按目标递推求解问题。另外,由于在连续的时间坐标下,动态规划算法无法实现,因此需要根据实际的精度要求设置最小时间单位,将时间离散化。一个最小时间单位称为一个时隙,一般一个时隙表示1~10 s是比较合适的,本文单位时隙取一个雷达扫描周期4 s。
2.2 贪心策略
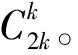
考虑在子节点的选取上引入贪心策略,降低子节点的数量及对比次数,以提高算法求解速度。举例来说,对于m层节点的某个子节点,假设某飞机x在跑道1的降落时间窗为[t1,t2],若t1 随机产生100个先到先服务飞机队列,对这100个队列进行优化调度,并统计优化结果,取其平均值作为算法的性能指标。 参数设置:机型配比(H,M,L)=(0.3,0.6,0.1);单位时隙4 s;时间窗跨度为100个时隙。 表2为算法运算性能比较(k=2)。由表2可知,未加贪心策略前双跑道动态规划算法的运算时间较长,效率不高。加入贪心策略后,由于算法的子节点数目以及比较次数大幅降低,算法运算速度在双跑道环境下提高了近100倍,计算时间大大缩短。另一方面,算法的优化效果也基本达到原动态规划算法的优化效果。这是由于保证了初始递推所需的信息后,随着递推一步一步地进行,贪心策略所丢失的信息量逐步得到弥补,使得效果可以接近原算法的效果。 表2 算法运算性能比较Table 2 Performance comparison of two algorithms 图1给出了平行双跑道总延误最小的优化结果。可以看出:算法优化效果随飞机数量增加逐步提升,这是由于当飞机数量较少时,其相对于大量飞机的可优化空间亦相对较小;不同的飞机数量和k值均会影响运算时间,但即使是70架飞机、k=3时用时也仅为2.53 s,完全能够满足实时调度的需求。 图1 平行双跑道优化结果Fig.1 Optimum results of parallel runways 本文针对飞机排序问题提出一种快速优化方法,在生成子节点时引入贪心策略,通过简化搜索过程的复杂度,提高算法运行效率。仿真结果表明,在保持优化效果相当的情况下,加入贪心策略后算法运算速度提高了近100倍,满足实际运行需求。 此外,本文的研究对象为平行双跑道相关运行模式下的飞机降落排序优化问题,但不失一般性,本文算法稍加修改即可应用于其他构型(多条跑道数大于3、交叉跑道等)和运行模式(独立运行、相关运行)下的飞机降落排序优化。 [1] Beasley J E,Krishnamoorthy M,Sharaiha Y M.Scheduling aircraft landings—the static case[J].Transportation Science,2000,34(2):180-197. [2] 王莉莉,顾秋丽.平行跑道到达航班排序问题研究[J].飞行力学,2013,31(6):566-569. [3] 王世东,张越,张智海,等.繁忙机场航班降落排序的多目标优化[J].交通运输系统工程与信息,2012,12(4):135-142. [4] Zhan Z H,Zhang J,Li Y.An efficient ant colony system based on receding horizon control for the aircraft arrival sequencing and scheduling problem[J].IEEE Transactions on Intelligent Transportation Systems,2010,11(2):399-412. [5] 孟祥伟,张平,李春锦.到场飞机排序及调度问题的Memetic算法[J].西南交通大学学报,2011,46(3):488-493. [6] 张勰,赵嶷飞,刘宏志.基于协同进化遗传算法的航班进港优化调度[J].交通运输系统工程与信息,2014,14(2):94-101. [7] Dear R G.The dynamic scheduling of aircraft in the near terminal area[R].Cambridge, Mass.: MIT,Flight Transportation Laboratory,1976. [8] Lee H,Hamsa B.Fuel cost,delay and throughput tradeoffs in runway scheduling [C]//Proceedings of the American Control Conference.Seattle:IEEE Press,2008:2449-2454. (编辑:方春玲) A fast optimization method for multi-runway aircraft landing sequencing ZHANG Xie, LIU Hong-zhi, ZHAO Yi-fei (Tianjin Key Lab of Operation Programming and Safety Technology of Air Traffic Management,Civil Aviation University of China, Tianjin 300300, China) Focusing on this typical combinatorial problem of sequencing the arrival aircraft for multi-runway, optimization model with minimum delay is established, and a dynamic programming algorithm based on greedy strategy is proposed. The greedy strategy is introduced while generating the nodes, and then reduces the searching complexity to improve the algorithm efficiency, so that the problem is solved that the computation efficiency decreases as the scale of the problem increases. Through the simulation, it is shown that the algorithm proposed here can simplify the searching process effectively, and the time is reduced effectively as the optimization effect is equivalent to the dynamic programming algorithm. The effectiveness of the algorithm is proved. air traffic flow management; landing sequencing; multi-runway; greedy strategy 2014-11-08; 2015-03-16; 时间:2015-05-13 17:14 国家自然科学基金资助(U1333108);国家科技支撑计划资助(2011BAH24B10);中央高校基本科研业务费专项资助(3122014C020) 张勰(1981-),男,陕西咸阳人,助理研究员,博士,研究方向为空中交通管理系统优化理论与方法。 V355.2 A 1002-0853(2015)05-0467-043 仿真算例
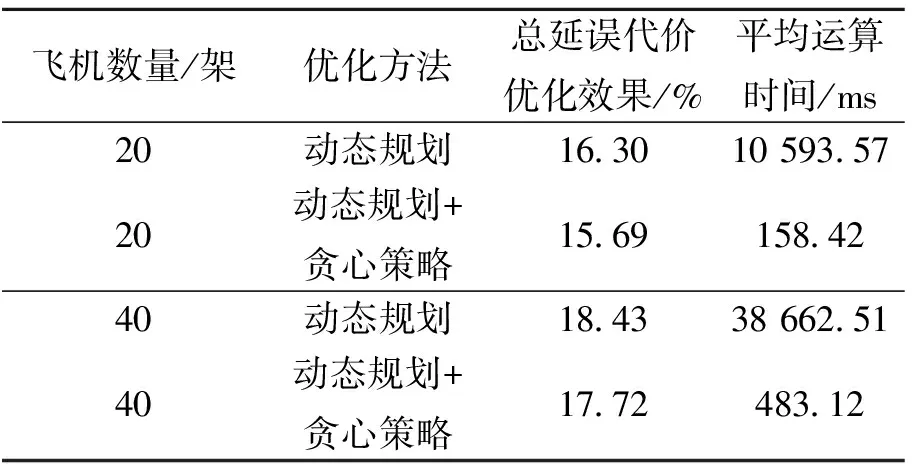
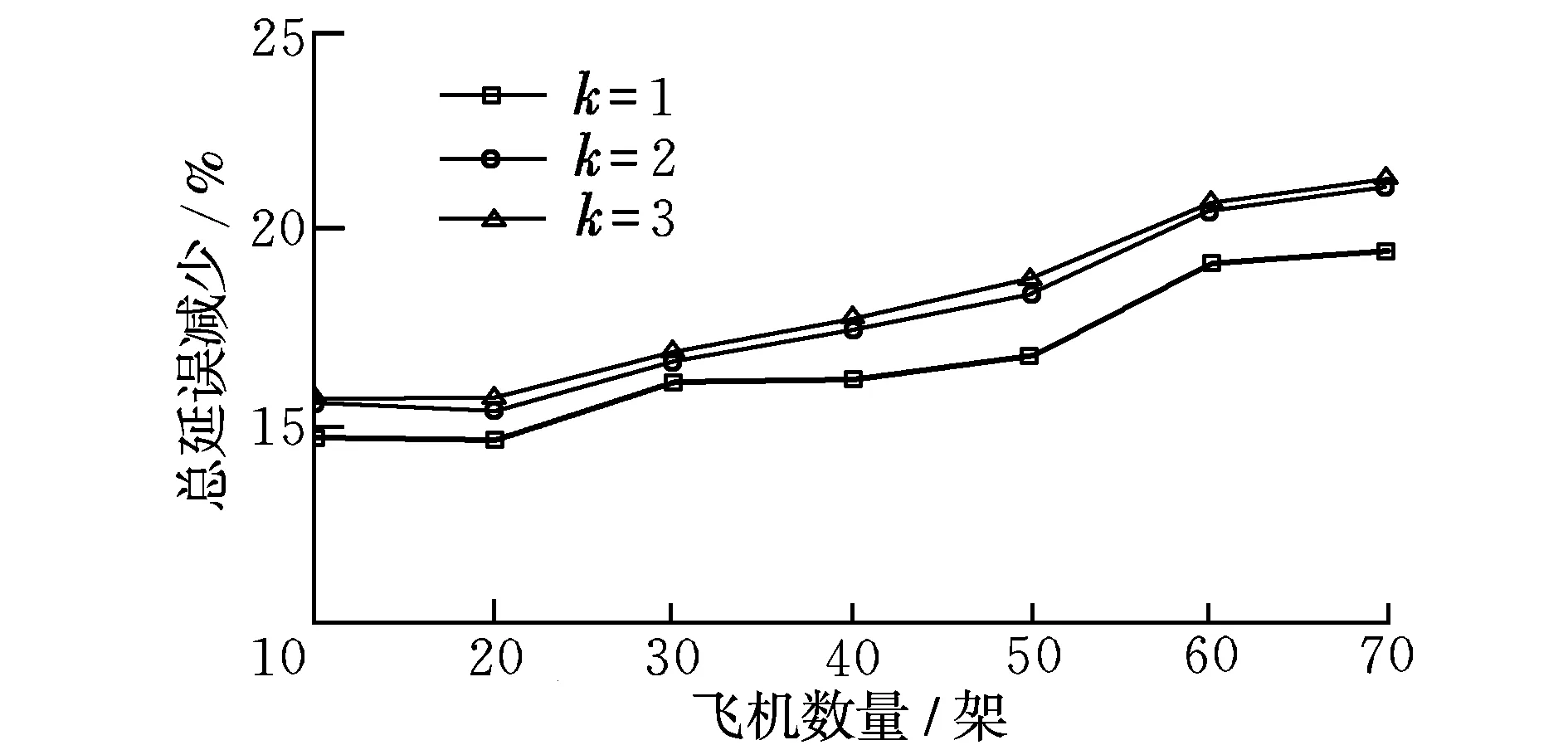
4 结束语
