基于突变级数法的创业板上市公司成长态势研究

吴应宇，朱兆珍，2

（1东南大学 经济管理学院，江苏 南京211100；2安徽财经大学 商学院，安徽 蚌埠233041）

2009年10月23日，创业板开板，成为众多高科技型、高成长中小企业的融资乐园。然而曾被寄望成为“中国纳斯达克”的创业板在4年之后却面临“成长的烦恼”。2014年前四个月，该板块指数“跌跌不休”①截止完稿，创业板指数月K图显示2014年前4个月持续下跌，6月开始稳定上升，但是9月出现暴涨。，六月开始稳定增长，但好景不长，九月突然骤增。创业板市场成长性备受质疑，不利于创业板市场健康有序发展。运用合理方法，探寻创业板市场成长规律迫在眉睫。目前，对一般上市公司静态性成长现状研究已相对比较成熟，但对其成长性进行动态趋势分析仍处于探索阶段，尤其是考虑系统潜在突变特性的研究并不多见。从静态的现状分析转向动态的态势评价是上市公司成长性研究的必然趋势。笔者拟采用突变级数法计算创业板上市公司成长指数，旨在有助于政府及其相关部门制定相应政策法规，投资者、债权人等利益相关者做出科学的财务决策，同时也尝试为创业板上市公司经营管理者制定发展战略提供参考。

一、突变级数法介绍

1.突变级数法的基本原理

法国数学家雷内·托姆（Rene Thom）教授在其1972年出版的奠基性著作《结构稳定性和形态发生学》中提出突变理论（Catastrophe Theory），齐曼将这一新的理论纳入“系统论”范畴，从而大大拓宽突变理论可能应用的范围。突变理论建于微积分、结构稳定性、奇点理论以及拓扑动力学等相关数学理论之上，被誉为“微积分以后数学的一次革命”，其应用遍及自然科学和社会科学，我国学者也对拓展突变理论的应用范围做出了贡献，如解释汉字字形辨识过程［1］。突变级数法的理论基础便是突变理论，它是一种通过对势函数及其临界点分类情况的研究来分析临界点附近的不连续表征。

2.突变级数法的实施步骤

突变级数法是一种通过分析势函数及其临界点分类情况来研究临界点附近不连续表征的模糊评价方法，再利用归一公式进行综合量化运算，最终归一为一个参数，这个参数即是要求的总的隶属函数，从而达到对评价目标进行排序分析的一种综合评价方法［2］。突变级数法有如下特点：① 无需对指标赋权；② 考虑了各评价指标的相对重要性；③ 减少了主观性又不失科学性、合理性；④ 计算简易准确，应用范围广泛［3-5］。下文将简要介绍突变级数法的实施步骤。

（1）构建多目标评价指标体系

根据评价目的，对评价总指标进行多层次分解，排列成倒立树状目标层次结构，并进行重要性排序，重要指标排在前面，次要指标排在后面，原始数据只需要知道最下层子指标的原始数据即可。因为一般突变模型状态变量的控制变量不超过4个，故相应的一般各层指标分解不宜超过4个。如果某层指标个数超过4个，可以采用因子分析法来进行指标提纯［6］。

（2）确定突变模型和归一化公式

突变模型有7种，但最常用的只有3种：尖点突变、燕尾突变和蝴蝶突变［7］。若一个指标仅分解为两个子指标，该突变类型可视为尖点突变；若一个指标可分解为三个子指标，可视为燕尾突变；如果一个指标能分解为四个子指标，可视为蝴蝶突变。突变级数法通过对势函数及其临界点分类情况的研究来分析临界点附近的不连续表征。在势函数中，有状态变量（内部变量）和控制变量（外部变量）两种变量，7种基本突变模型见表1。

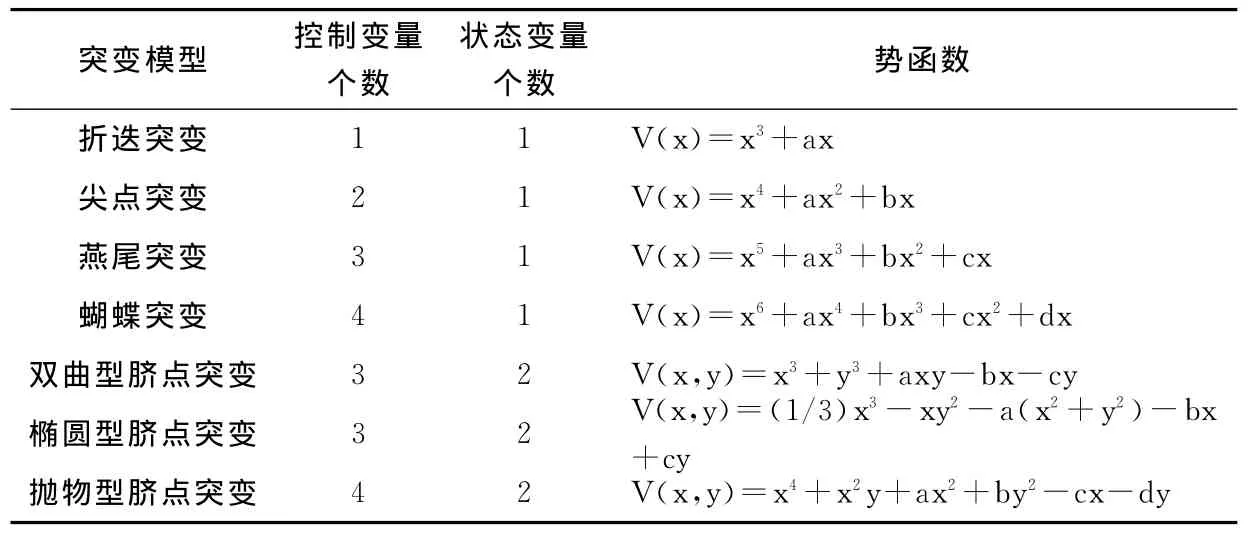
表1 基本突变模型

上表中突变模型的名称得名于各模型分歧集的形状，在各势函数中，V（x）表示一个系统的一个状态变量x的势函数；V（x，y）表示两个状态变量的势函数；x，y为状态变量；状态变量的系数a，b，c，d表示该状态变量的控制变量。上述七种突变皆由各自势函数决定，某种类型突变全过程可通过其相应的平衡曲面M来描述，M由突变系统的势函数f（x）其所有临界点集合而成，可通过对V（x）求一阶导数得到，即 V′（x）＝0，它的奇点集通过对 V（x）求二阶导数得到，即 V″（x）＝0。由 V′（x）＝0和V″（x）＝0两方程联立可消去x，得到突变系统的分歧点集方程。通过分解形式的分歧点集导出归一公式，由归一公式将系统内诸控制变量不同的质态化为同一质态，即化为状态变量表示的质态。

尖点突变势函数为：V（x）＝x4＋ax2＋bx；平衡曲面方程 M：V′（x）＝4x3＋2ax＋b＝0

奇点集S：V″（x）＝12x2＋2a＝0；求解联立方程

可得分歧集方程：8a3＋27b2＝0；进一步可解得在此只表示对应的a的x值，xb表示对应b的x值）。如果令｜x｜＝1，则有a＝-6，b＝8，这样评价决策时状态变量x和控制变量a、b的取值范围也得以确定，即｜x｜＝0～1，｜a｜＝0～6，｜b｜＝0～8。然而这样取值会导致x、a、b的取值范围不统一，与效用函数、模糊隶属函数0～1的取值范围大相径庭。为了运算方便，必须把状态变量和控制变量的取值范围按照“突变级数加减乘除后决策结果不变”的原则进行改造。因此，只要把a缩小6倍，b缩小8倍即可得到尖点突变模型的归一公式。具体过程如下取｜x｜＝1，则｜a｜＝6，如果把a缩小6倍，令a′＝1，则有a＝a′×6，所以如此一来，a′比原来的a取值范围缩小了6倍，变为0-1之间。同理可把b的取值范围转化为0-1之间。如此得到尖点突变的归一化公式（详见表2）。

表2 常用突变模型势函数及归一化公式

（3）利用归一公式进行评价

根据多目标模糊决策理论，在多种目标函数下，对同一方案，如设A1，A2，…，Am为模糊目标，则理想的策略为：C＝A1∩A2∩…∩Am，其隶属函数为：L（x）＝LA1（x）∧LA2（x）∧ … ∧LAm（x），式中LAi为Ai的隶属函数，定义为Ai的隶属函数，即为各目标隶属函数的最小值。对于不同的方案，如设H1，H2，…，Hn，记Hi的隶属函数为LHi（x）＞LHj（x），则表示方案Hi优于方案Hj，因而利用归一公式对同一对象各个控制变量（指标）计算出的对应指标值应遵循“大中取小”原则，也称为“就低不就高”原则；但对存在互补关系的指标，通常用其平均数代替。判断互补类型的原则是：若同一对象各个控制变量之间存在弱相关关系则称该对象各控制变量为“非互补”类型；若同一对象各控制变量之间可以互相弥补不足之处，则称该对象各控制变量为“互补”类型。

二、创业板上市公司成长态势分析

1.创业板上市公司成长性的突变适宜性分析

突变理论认为初等突变现象通常遵循5个基本特征，即多模态、不可达性、突跳、发散和滞后［8］123。一般情况下，所研究的科学问题中出现上述两个以上特征时，就可以运用突变模型进行定性分析［9］。创业板上市公司多为高科技中小企业，无论从行业还是规模来看，都面临较高财务风险。首先，创业板作为一个年轻板块，在不断进行动态的自我调整，因此会出现加速成长、低速成长抑或负成长情态；但是如果创业板上市公司面临的风险超过一定限度，无法通过自我调整进行管控，将会陷入困境、面临危机甚至摘牌或破产；另外，当创业板上市公司成长态势的重要控制变量如盈利能力或技术创新能力发生变化，会引起成长态势连锁反应，但是具有滞后性［10］。上述分析特点与突变指征多模态、不可达性、突跳性和滞后性基本一致。因而，采用突变级数法构建相应突变模型对创业板上市公司成长态势进行分析是可行的。目前对创业板上市公司成长性进行测量采用较多的是主成分分析法［11］、因子分析法［12］、熵值法［13］，也有学者采用上述方法与突变级数法相结合［13-15］。然而，现有研究多就某一年或连续几年取平均值的横截面数据展开静态探讨，反映不出创业板上市公司的成长趋势。本文遵循数据的可靠性、可获得性和系统性等原则，拟选取第一批在创业板上市的28家企业为研究对象，时间跨度为2010年1月1日至2013年12月31日，使其在纵向深度做到“知己”，掌握成长趋势，制定发展战略；在横向对比中“知彼”，寻找发展差距，进行合理定位。

2.数据来源及数据预处理

初始研究样本来源于创业板开板时第一批上市公司28家，以半年为研究周期，时间跨度为2010年1月1日至2013年12月31日①考虑到创业板开板时间晚，首批上市公司只有28家，而创业板上市公司成长环境瞬息万变，且成长态势研究需要多期数据，因此选取半年为研究周期。，共计8期。数据来源于CSMAR国泰君安数据库和RESSET金融研究数据库公司半年报和年报。

反映上市公司成长性的不同类型指标往往具备不同的量纲和量纲单位。为了消除由此产生的不可通度性，在此运用朱顺泉［16］使用的极差变换法，对财务成长性指标进行无量纲化处理。具体操作如下：

对于值越大越好的正指标，令

对于值越小越好的负指标，令

对于指标值最好处于［g1j，g2j］之间的适度指标，令

3.构建财务成长性指标体系

Elizabeth认为成长比增长含义丰富，它既包括量的增长又包括质的提高。量的增长即企业规模的扩张［17-18］。Erkki and Laitinen认为质的提高表现为环境适应能力和技术创新能力的增强等方面，是成长的最根本标志［19］。创业板主要为高科技型企业提供直接融资渠道，如果公司能够持续创新、经营有方、进行有效风险管理和合理控制增长速度，创业板上市公司将会踏上良性成长的道路。本文借鉴国内外相关文献［20-25］，结合我国创业板上市公司成长实情，初步选取如下指标：开发支出、基本每股收益增长率、净利润增长率、总资产增长率、固定资产投资增长率、净资产收益率、销售净利率、资产报酬率、总资产周转率、应收账款周转率、资产负债率、流动比率、速动比率。

突变理论告诉我们，可能出现的性质不同的不连续构造的数目由控制变量a，b，c，d的数目决定，而并非取决于状态变量x，y的数目。一般状态变量数目可能很大，而控制变量数目一般不会超过5［1］，这也进一步说明使用突变级数法必须保证构建评价指标体系时相应的各层指标分解数目小于或等于4。

下文将通过因子分析法对众多指标进行筛选，消除多重共线性，同时依据因子贡献率大小确定指标重要性，满足突变级数法建模时“重要指标排在前面、次要指标排在后面”［2］的要求，避免仅凭内在矛盾和变量作用机制经验确定重要性排序的主观性。然而因子分析法只适用于各指标之间存在线性关系，若存在非线性关系，评价结果会有失客观，而突变级数法正好可以弥补这一不足。本文借鉴胡静等学者［15］的做法，扬长避短，运用因子分析法确定各层指标的重要性，再运用突变级数法进行综合评价。

在因子分析的相关系数矩阵中，资产报酬率与净资产收益率和基本每股收益增长率相关系数分别为0.954和0.923，存在信息重叠（限于篇幅，相关系数矩阵未列出），故将资产报酬率指标剔除。同理，剔除总资产增长率。余下十一个指标重新进行因子分析。结果如图1：

图1 KMO和Bartlett的检验

图1显示，通过KMO和Bartlett检验，8期样本汇总数据分析KMO值等于0.629，大于0.05，且Sig值为0.000，小于显著性水平0.05，因此适合做因子分析。

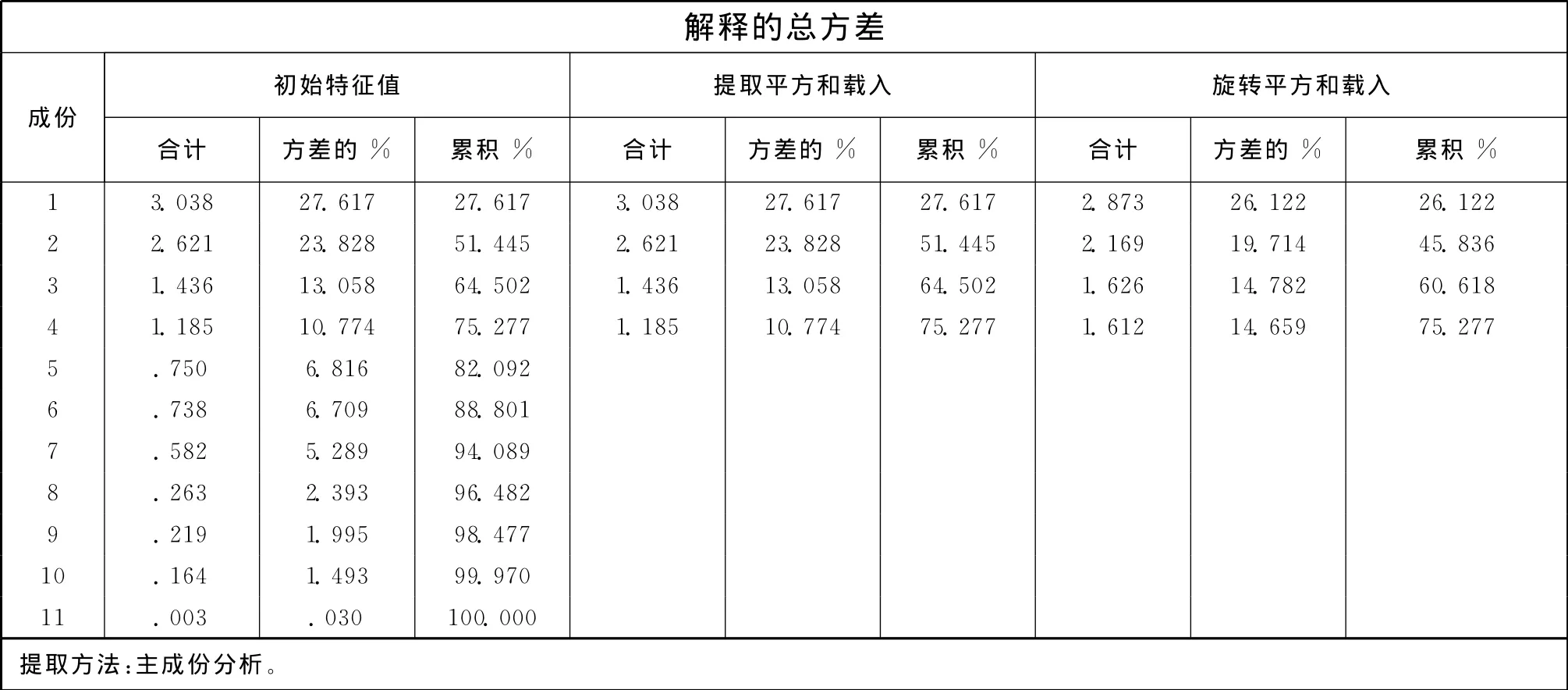
图2 方差贡献率

图2给出了方差贡献率结果，很明显可以看出，前4个因子的特征值大于1，并且特征值之和占总特征值的75.277%，因此可以提取前4个因子作为主因子。

图3 旋转的因子载荷

图3给出了旋转后的因子载荷值，可以看出每个因子只有为数不多的几个指标的因子载荷比较大，因此可以依据上图进行指标分类：第一个因子与“流动比率”、“速动比率”和“资产负债率”相关性最强，所以可以将第一个因子用来反映创业板上市公司的偿债能力，并称为“偿债因子”；第二个因子与“基本每股收益增长率”、“净利润增长率”、“净资产收益率”和“销售净利率”四个指标最为相关，可以用来衡量创业板上市公司的盈利能力，称为“盈利因子”；第三个因子与“应收账款周转率”和“总资产周转率”关系最为密切，可以测量创业板上市公司的营运能力，称为“营运因子”；第四个因子与“固定资产投资增长率”和“开发支出”相关性最强，可以用来解释创业板上市公司发展能力，称为“发展因子”。

按照四个因子的方差贡献率及各个指标与因子间的相关性大小排序，最终构建创业板上市公司成长性指标体系如图4所示，因素层指标重要性排序与胡静等学者的研究［15］相同，他们研究中小型农业上市公司成长性问题，因为研究对象不同，最底层指标选择及其重要性排序存在稍许差异。

4.确定评价指标各层次的突变系统类型

图4 创业板上市公司成长性指标体系

严格按照突变级数法的实施步骤（2）以及（3）提供的评价决策的“互补”和“非互补”原则，确定各层指标的突变类型。因素层指标：偿债能力指标为燕尾突变系统，盈利能力指标为蝴蝶突变系统，营运能力指标和发展能力指标皆为尖点突变系统。四者均为互补型。目标层指标——创业板上市公司成长性指标评价体系为蝴蝶突变系统，也为互补型。

5.利用归一化公式进行成长态势评价

先采用公式（1）对反映盈利能力、营运能力和发展能力的各最底层指标数据进行无量纲化处理，利用公式（3）和（4）对偿债能力指标进行无量纲化处理。按照国际惯例，速动比率适度值为100%、流动比率适度值为200%、资产负债率适度值为30%-60%［16］，再套用相应突变模型归一化公式进行综合评价。

三、计算实例及实证结果

依据以上步骤以样本公司中第一家上市公司特锐德（300001）2010年第一期数据为例计算创业板上市公司成长指数。其它样本公司同理计算。

首先，计算第二层即因素层指标值。

偿债能力分解为三个子指标，是燕尾突变系统，为互补型指标，采用互补取平均值原则。故偿债能力水平为：

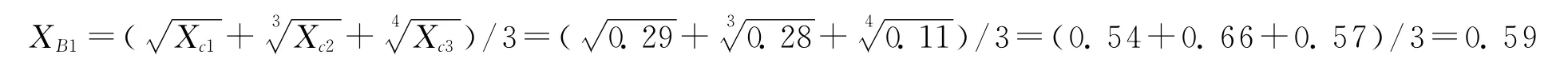
盈利能力分解为四个子指标，是蝴蝶突变系统，为互补型指标，采用互补取平均值原则。故盈利能力水平为：

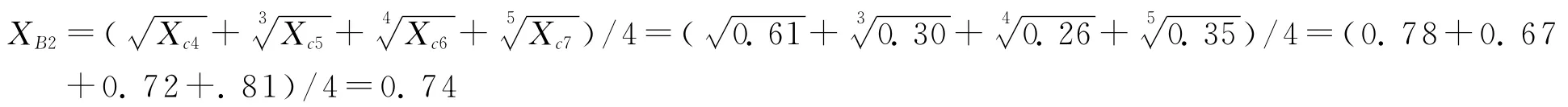
营运能力分解为两个子指标，是尖点突变系统，为互补型指标，采用互补取平均值原则。故营运能力水平为：

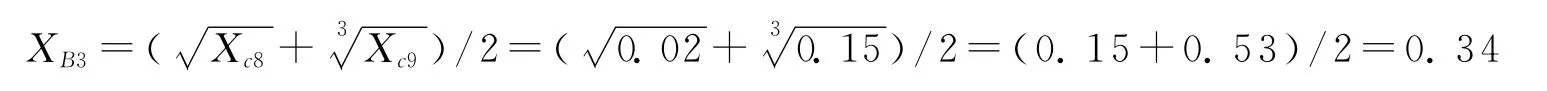
发展能力分解为两个子指标，是尖点突变系统，为互补型指标，采用互补取平均值原则。故发展能力水平为：

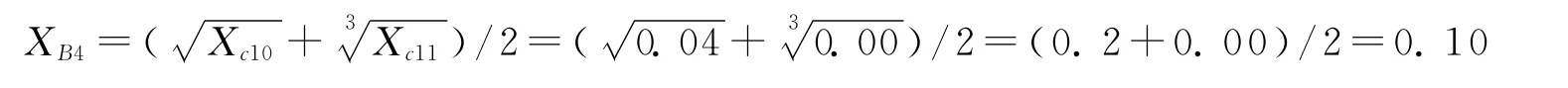
其次，计算一级指标财务成长性水平。

财务成长性总指标分解为四个子指标，是蝴蝶突变系统，四个指标之间可以弥补彼此不足，为互补型指标，采用互补取平均值原则。故特锐德2010年第一期成长性水平亦即成长指数为：

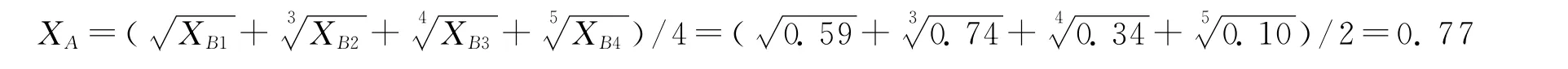
特锐德2010年6月30日偿债能力、盈利能力、营运能力和发展能力指标值分别为0.59、0.74、0.34和0.10，偿债能力尚可，盈利能力较强，营运能力欠佳，发展能力落后。从《青岛特锐德电气股份有限公司2010年半年度报告》了解到，特锐德公司加大对石油管道、电力、煤炭等市场的开拓力度，因此报告期内在电力系统、煤炭系统的销售收入大幅增加，表现出较强的盈利势头；但是销售收入并非收现，同期应收账款增加34%。又因为购买原材料等经营性支出增加，公司每股经营活动产生的现金流量净额较去年同期下降460%，经营活动产生的现金流量净额减少，故影响了偿债能力；公司新增订单交货周期较长，应收账款周转率和总资产周转率降低，导致营运能力不佳；报告期内特锐德公司正在执行一些诸如为宁杭铁路客运专线和哈大客运专线提供铁路电力远动箱式变电站等产品、为新疆昌吉市光正电力有限责任公司提供35kV智能箱式变电站等产品的金额较大合同，未发生开发支出，固定资产投资幅度也较低，导致发展能力指标值很小。由此看来，采用突变级数法计算的指标值比较准确地反映了特锐德公司的现实状况，运用突变级数算法核算创业板上市公司成长指数并评价其成长态势是合理的。

按照上述步骤可以计算出其它样本公司的偿债能力、盈利能力、营运能力、发展能力及财务成长性综合水平，即成长指数。限于篇幅，具体指数未列出，表3对成长指数进行了简要描述。

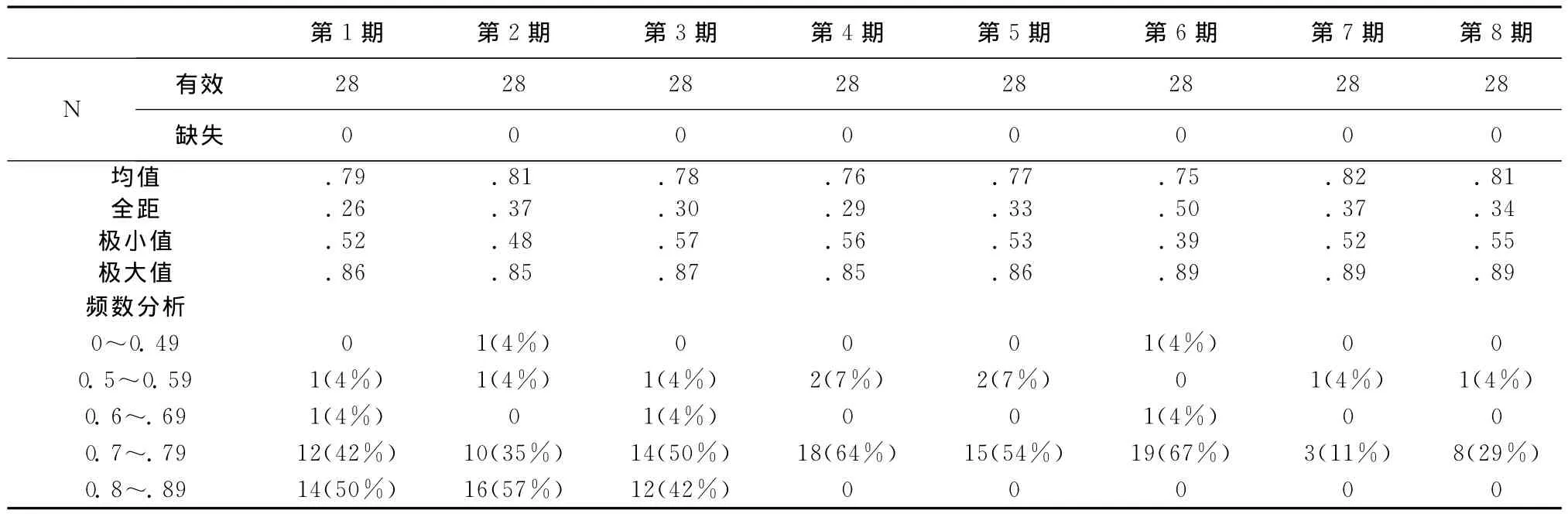
表3 描述统计量

表3有助于我们了解首批在创业板上市的28家企业成长指数概况。8期成长指数均值处于0.80左右。成长指数最大值在后3期，为0.89，最小值仅为0.39。从全距来看，这28家上市公司在第6期即2012年12月31日差距最为明显。依据频数分析结果，成长指数基本呈现“两头小、中间大”的一般规律。

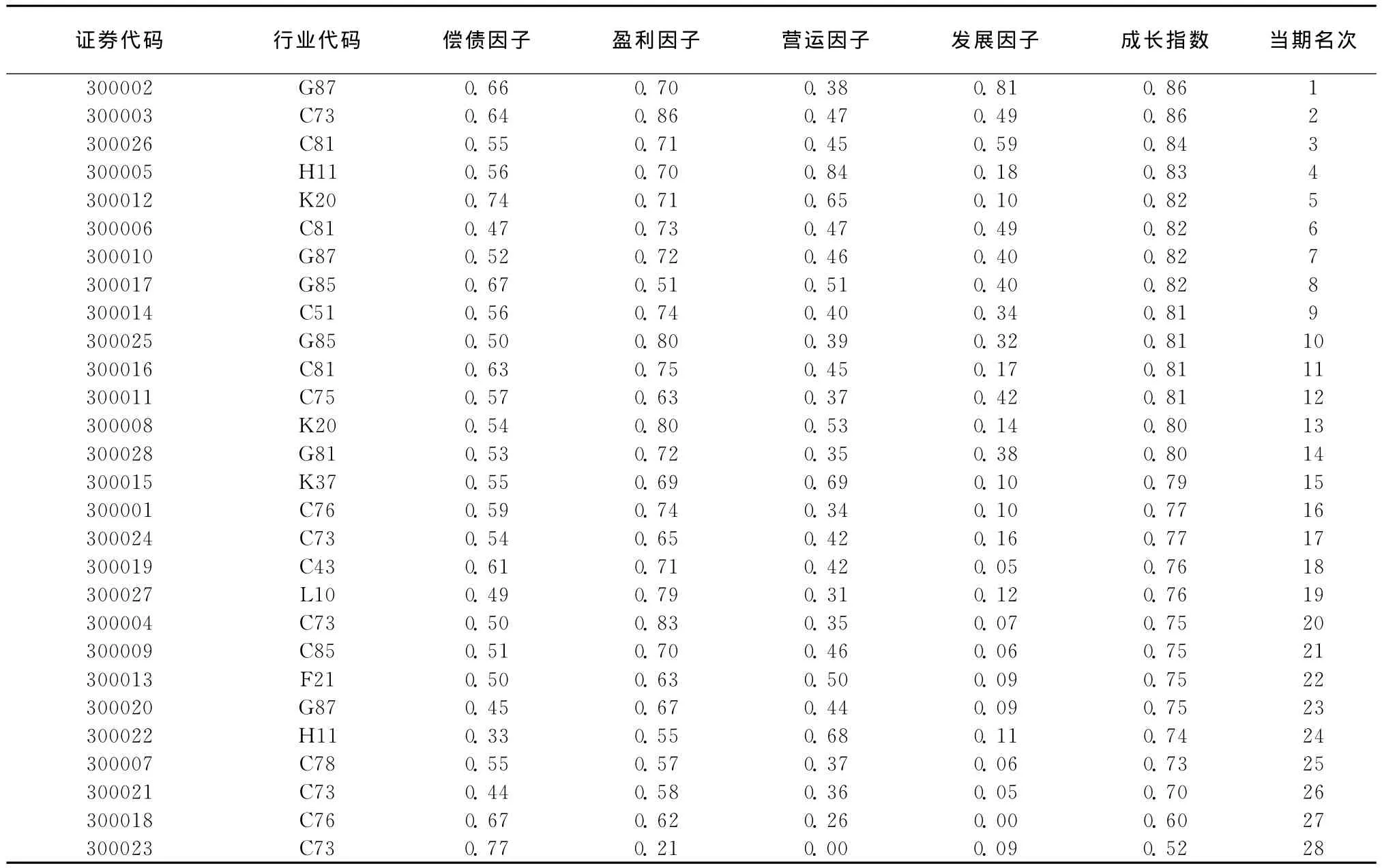
表4 第一期创业板上市公司财务成长因素层指标值

表4数据显示，每家创业板上市公司财务成长因素可分解为偿债能力、盈利能力、营运能力和发展能力四大方面并进行量化，可知悉创业板上市公司财务成长具体影响因素及影响程度。如成长性最佳的300002神州泰岳，其成长指数为0.86，相对较高，这得益于较强的发展能力和盈利能力，分别达到0.81和0.70。但是营运能力指标值只有0.38，营运状况不佳。偿债能力指标值0.66，横向比较偿债能力较强，与其它因素相比，对成长指数贡献不明显。神州泰岳预踏上良性成长之路，需要优化经营活动，提高营运能力。从行业结构方面来看，首批28家创业板上市公司主要集中于电子信息、现代服务和生物医药等行业，这三大行业占比高达88%①根据深交所上市推广部撰写报告《首批28家创业板上市企业基本情况》整理而得。。从成长指数排名来看，指数大小与行业类型关系不大，说明行业异质性对创业板上市公司成长指数没有明显影响。

下文将通过作图研究创业板上市公司成长指数与创业板指数走势规律。图5对8期成长指数的平均值作折线图（每年6月30日和12月31日若是节假日则以最接近一日指数替代），明显看出成长指数呈波浪形波动，且具有一定周期性。2010年，国内刚开始经济结构调整，宏观经济基本处于上行周期，国家政策倾斜外围市场也相对较为平静，因此创业板呈现上扬趋势。但是正如首创证券研发部总经理王剑辉所说，创业板上市公司无法完全取代部分传统产业，不可能成为整个国民经济的支柱，高科技新兴产业在更多层面只能起到“经济助推器”的作用，不能充当主力。随着前期的持续走高，新兴产业估值空间已被透支，创业板泡沫破灭，创业板成长遇挫，2012年末见底。2013年以来，“稳增长”政策频繁出台，影响了市场预期，投资者对政策救经济抱有希望，创业板则以一波气势磅礴的走势，屡创新高。这些变化都在创业板上市公司成长指数态势图中得到很好体现。

图5 创业板上市公司成长指数态势

创业板指数是从创业板市场中选取100只成分股采用派氏加权法进行综合计算而得，成分股每季度调整一次，以及时反映创业板上市公司成长特点（表5）。图6显示，开盘指数、收盘指数、最高和最低指数态势图几乎重合，故以任何一个指数作为参照对象对结果没有影响。比较图5和图6折线图，显而易见，两条线波动轨迹基本保持一致。表明，创业板上市公司成长态势与创业板指数走势密切相关。100只创业板指数样本股票中大部分都属于高科技企业，其变化趋势可以恰到好处地预测作为高科技企业摇篮的创业板块的上市公司成长态势。

图6 创业板指数变动趋势

四、结 论

本文采用因子分析法筛选指标并确定指标重要性，为使用突变级数法做好铺垫，并依据突变级数法原理构建了创业板上市公司成长态势评价模型。通过对28家首批创业板上市公司于2010年1月1日至2013年12月31日四年间相关指标值进行递归演算得到各期成长指数。从各期成长指数简要描述表不难看出，8期成长指数均值均为0.8左右，整体波动不大。频数分析结果显示，各期成长指数分布基本呈“两头小，中间大”的一般规律。从行业结构分析成长规律，首批28家创业板上市公司聚集于电子信息、现代服务和生物医药三大行业，占比高达88%，但是各行业公司成长指数大小与行业类型关系不明显，说明行业异质性对创业板上市公司成长指数影响不显著。

通过比较图5与图6可以发现，创业板上市公司成长指数变动趋势与创业板指数波动轨迹基本一致。这一发现对投资者与债权人等利益相关者做出科学财务决策以及创业板上市公司高层管理者进行自我诊断制定发展战略具有一定的实践价值。然而，鉴于样本数量限制及所选期间约束，研究结论仅供参考。

［1］都兴富.突变理论在经济领域的应用（下）：股票分析多准则决策［M］.成都：电子科技大学出版社，1994（5）：22.

［2］桑博德.突变理论入门［M］.上海：上海科学技术文献出版社，1989：22-25.

［3］Wu Q，Xie K F，Chen Z Y.A Catastrophe Model on the Evaluation and Classification of Mine Disaster Rescue Measures［J］.Systems Engineering Procedia，2012（4）：484-489.

［4］Zhang L X，Liu X，Li D L.Evaluation of the Rural Ⅰnformatization Level in Four Chinese Regions：A Methodology Based on Catastrophe Theory［J］.Mathematical and Computer Modeling，2013（58）：868-876.

［5］陈晓红，杨立.基于突变级数法的障碍诊断模型及其在中小企业中的应用［J］.系统工程理论与实践，2013（6）：1479-1485.

［6］李柏洲，苏屹.基于改进突变级数的区域科技创新能力评价研究［J］.中国软科学，2012（6）：90-101.

［7］Baumol，William J，Blackman［J］.Wolff，Edward N.Unbalanced Growth Revisited：Asymptotic Stagnancy and New Evidence［J］.American Economic Review，1985，75（4）：806-817.

［8］桑博德.突变理论及其应用［M］.上海：上海交通大学出版社，1988.

［9］朱正威，胡永涛，郭雪松.基于尖点突变模型的社会安全事件发生机理分析［J］.西安交通大学学报，2011，31（3）：51-56.

［10］张信东，薛艳梅.R＆D支出与公司成长性之关系及阶段特征——基于分位数回归技术的实证研究［J］.科学学与科学技术管理 ，2010（6）：28-33.

［11］梁毕明.我国创业板上市公司成长性研究［J］.经济纵横，2012（8）：103-106.

［12］Jian-wen WANG，Cheng HUANG.Analysis on Affecting Factors to the Growth of the Listed Companies on GEM of China［C］.The 18th Ⅰnternational Conference on Ⅰndustrial Engineering and Engineering Management，2011，8：43-46.

［13］王朝勇，唐亮，张显峰.我国创业板上市公司成长性评价和关联分析［J］.工业技术经济，2013（4）：60-67.

［14］黎东升，秦志岗.基于因子分析的农业类上市公司竞争力突变综合评价［J］，农业技术经济，2011（2）：96-101.

［15］胡静，黎东升.我国中小型农业上市公司成长性实证研究［J］.农业技术经济，2013（3）：121-125.

［16］朱顺泉.上市公司财务预警统计与智能建模及应用研究［M］.北京：人民出版社，2013.

［17］Elizabeth Webster.The Growth of Enterprise Ⅰntangible Ⅰnvestment in Australia ［J］Ⅰnformation Economics and Policy，2000，（12）.

［18］Coase R H.The Nature of the Firm［J］.Economics，1937（4）：386-405.

［19］Erkki K，Laitinen A.Dynamic Performance Measurement System：Evidence from Small Finnish Technology Companies ［J］.Scand.J.Mgmt，2002，（18）.

［20］吴世农，李常青，余玮.我国上市公司成长性的判定分析和实证研究［J］.南开管理评论，1999（4）：49-57.

［21］徐维爽，张庭发，宋永鹏.创业板上市公司成长性及技术创新贡献分析［J］.现代财经，2012（1）：63-68.

［22］Delmar F，Davidsson P，William W B.Gartner.Arriving at the High-growth Firm ［J］.Journal of Business Venturing，2003（18）：189-216.

［23］Shane S.The Ⅰllusions of Entrepreneurship：The Costly Myth That Entrepreneurs，Ⅰnvestors and Policy Makers Live By ［M］.New Haven：Yale University Press，2008.

［24］赫连志巍，宋晓明.基于突变级数法的高技术产业升级能力评价研究［J］.科学学与科学技术管理，2013（4）：98-103.

［25］陈守东，陶治会.基于突变级数的创业板成长性研究［J］.证券市场导报，2013（4）：50-54.